引用本文
王连坤, 方伍宝, 段心标, 胡光辉, 李振春, 万弘. 基于互相关误差泛函的最小二乘逆时偏移方法[J]. 物探与化探, 2016,40(5): 980-985.
WANG Lian-Kun, FANG Wu-Bao, DUAN Xin-Biao, HU Guang-Hui, LI Zhen-Chun, WAN Hong. A cross-correlation objective function for least-squares reverse migration[J]. Geophysical and Geochemical Exploration, 2016,40(5): 980-985.
Doi:10.11720/wtyht.2016.5.22  
Permissions
Copyright©2016, 物探与化探编辑部
© 《物探与化探》编辑部
基于互相关误差泛函的最小二乘逆时偏移方法
王连坤1,2, 方伍宝1, 段心标1, 胡光辉1, 李振春2, 万弘1,2
1.中国石化石油物探技术研究院,江苏 南京 211103
2.中国石油大学(华东) 地球科学与技术学院,山东 青岛 266580

作者简介: 王连坤(1991-),男,硕士研究生,主要从事地震波传播与成像方面的研究工作。

收稿日期: 2016-03-09
基金: 国家科技重大专项(2016ZX05014-001-002)
摘要

最小二乘偏移可以得到成像质量更高的剖面,有利于更好地进行岩性储层成像和储层参数反演。但是,最小二乘偏移在实用化过程中却很难实现其高精度岩性成像的目标。在分析传统的最小二乘偏移存在的问题后,发展了一种基于相位匹配的最小二乘偏移方法,该方法舍弃了传统的二次型泛函,采用互相关泛函,更多地强调相位信息在最小二乘偏移中的作用,在理论上可以更好地适用于实际资料。通过对互相关误差泛函构建、逆时反偏移合成预测数据、梯度预条件处理、共轭梯度法迭代求解等方面进行研究,探索实现了基于互相关误差泛函的最小二乘逆时偏移方法。简单凹陷模型和复杂salt模型测试表明,本文方法具有较好的适用性和有效性。

关键词: 互相关误差泛函; 最小二乘逆时偏移; 相位匹配; 预条件共轭梯度法
中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)05-0980-06 doi: 10.11720/wtyht.2016.5.22
A cross-correlation objective function for least-squares reverse migration
WANG Lian-Kun1,2, FANG Wu-Bao1, DUAN Xin-Biao1, HU Guang-Hui1, LI Zhen-Chun2, WAN Hong1,2
1.Sinopec Geophysical Research Institute,Nanjing 211103,China
2.School of Geoscience,China University of Petroleum (East China),Qingdao 266580,China
Abstract

The least-square migration methods can make the seismic profile imaging quality higher,and are conducive to better imaging for lithologic reservoir and reservoir parameter inversion.However,in the process of practical application,it is very difficult for least square migration to achieve high accuracy of lithology imaging.Based on an analysis of the problems existing in the traditional least squares migration,the authors have developed a least squares migration method based on phase matching,which abandons the quadratic function used frequently by the traditional methods,and employs the cross-correlation function;in this way,this method emphasizes more on the role of the seismic phase information in the least squares inversion imaging;in theory,and it can be better applied to real data.Based on the cross-correlation function building,synthesizing prediction data by reverse time demigration,gradient precondition,and pre-conditional conjugate gradient,the authors explored and realized a cross-correlation objective function for least-squares reverse migration.Simple sub-sag model and complex salt model tests show that the proposed method has applicability and effectiveness.

Keyword: cross-correlation objective function; least-squares reverse migration; phase matching; preconditioned conjugate gradient method

从基于射线理论的Kirchhoff偏移和Beam偏移, 到基于单程波方程的波动方程偏移, 再到RTM, 地震偏移技术在对地下构造成像方面发挥着越来越重要的作用。现阶段, RTM是解决地下复杂构造成像问题最先进的技术[1, 2, 3, 4], 它基于真振幅成像理论, 能够自动补偿偏移过程中的几何扩散现象, 得到独立于角度的反射系数。然而, RTM的理论假设地震数据采样规则、接收孔径无限大、观测数据中无假频、偏移速度较为精确等, 而这些假设在实际生产中很难实现[5, 6]。针对这些问题, 许多地球物理学家开展了基于反演理论的地震成像方法— — 最小二乘偏移(least squares migration, LSM)方面的研究。最小二乘偏移的思想最早是由LeBras等提出[7], Dai等[8, 9]针对同步震源数据提出了LSRTM, 并采用了去模糊化滤波器作为预条件算子加速收敛; Wong等[10]将LSRTM应用到了海洋资料, 得到了较好的成像结果; Dai和Schuster[11]发展了平面波最小二乘逆时偏移; Dutta和Schuster[12]在LSRTM中引入了黏声波动方程算子, 实现了衰减补偿; 黄建平等[13]将LSRTM成功地应用到近地表保幅成像中; 郭书娟等[14]探索实现了针对陆地资料的LSRTM; Lin等[15]在LSRTM中引入改进的总变差正则化, 压制偏移噪声, 提高收敛速度。

最小二乘偏移理论是在Born近似下匹配预测数据和实际观测数据, 从而得到成像质量更高的剖面, 有利于更好地进行岩性储层成像和储层参数反演。但是, LSM在实用化过程中却很难实现其高精度岩性成像的目标[16, 17, 18], 其原因主要有:①地球介质至少为变密度的粘弹性介质, LSM成像过程中一般采用声波方程, 模拟过于简单; ②在波场模拟过程中震源子波的定义非常困难, 不同的单炮记录其对应的震源子波也不同, 此外, 当地下介质为强吸收衰减时震源子波空变剧烈。这些因素导致LSM过程中很难得到准确的振幅信息, 而常规的LSM却是基于振幅匹配的, 其对振幅精度的要求很高, 因此, 所有的这些实际问题需要在处理观测数据和模拟数据时付出很大的努力。Zhang等[19]、Dutta等[20]在LSM过程中使用了互相关误差泛函, 在反演成像过程中更多地强调相位信息的作用, 在一定程度上降低了LSM对振幅精度的限制, 加速了LSM的实用化进程。

目前, 基于互相关误差泛函的最小二乘逆时偏移方法的研究主要集中在国外, 国内尚未见到相关方面的文献资料。笔者在前人研究的基础上, 分别从互相关误差泛函构建、逆时反偏移合成预测数据、梯度预条件处理、共轭梯度法迭代求解等方面进行研究, 探索实现了基于互相关误差泛函的最小二乘逆时偏移方法。简单凹陷模型和复杂salt模型测试表明, 文中提出的方法具有较好的适用性和有效性。

1 方法原理

常规的最小二乘偏移通常可以看作最小化二次型误差泛函的最优化反演问题:

E(m)=12‖Lm-dobs‖2, (1)

其中, E(m)表示误差泛函, dobs表示实际观测数据, m为模型参数, L为波场模拟算子, 即反偏移算子。

前人研究指出, 基于振幅匹配的常规最小二乘偏移在处理实际问题时很难实现其高精度岩性成像的目标, 这主要是由于反演成像过程中的振幅不准确导致的。因此, 研究基于互相关误差泛函的最小二乘偏移显得很有必要。

基于此, 建立式(2)所示的目标函数:

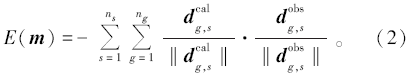
其中:E(m)表示互相关误差泛函, 其值分布在0和-1之间, 在迭代收敛过程中, 其值逐渐逼近-1; dg, sobs表示实际观测数据, m表示模型参数, dg, scal表示反偏移重构数据。文中采用逆时反偏移方法对数据进行重构, 其算法为[21]:

1v2(x)∂2∂t2-∇2PS(x, t, xs)=δ(x-xs)f(t), 1v2(x)∂2∂t2-∇2PR(x, t, xs)=r(x)PS(x, t, xs), d(xr, t, xs)=PR(xr, t, xs)。3

此处, 式(3)中的d(xr, t, xs)即为式(2)中的 dg, scal。

Aoki和Schuster[22]研究提出, 用一个去模糊化算子d-1=(LTL)-1作为LSM的预条件算子, 可以提高收敛速度。但是, 在现有计算条件下很难计算全Hessian矩阵的逆H-1。陈生昌等[23]提出, 在最小二乘偏移过程中, 先求取Hessian矩阵的一个不甚精确的近似解作为LSM实现过程中的预条件, 也可以加快迭代收敛速度。鉴于Hessian矩阵是主对角占优的矩阵, 因此采用Hessian矩阵的对角元素近似代替Hessian矩阵对梯度进行预处理, 该近似Hessian矩阵可以表示为:

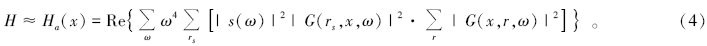
基于互相关误差泛函的最小二乘偏移在数学上是一个最优化问题, 研究中采用预条件共轭梯度法进行迭代反演成像, 其迭代过程为:

1) 根据式(2)计算泛函的梯度, gk(i+1)表示第i+1次迭代的梯度;

2) 用共轭梯度公式更新梯度: dk(i+1)=C gk(i+1)+β dk(i),

其中, β = (gk(i+1))TCgk(i+1)(gk(i))TCgk(i), C=H-1, 为预条件算子;

3) 计算迭代步长:

α = (dk(i+1))Tgk(i+1)(Ldk(i+1))T(Ldk(i+1)), 其中L为反偏移算子;

4) 更新反射系数图像:m(i+1)=m(i)-α dk(i+1);

5) 检查是否满足成像精度要求, 若满足, 则停止迭代, 输入成像结果; 反之, 则返回步骤1), 进行下一次迭代。

2 数值测试

为验证基于互相关误差泛函的最小二乘逆时偏移方法的有效性和稳定性, 采用经典的凹陷模型和复杂的salt模型进行数值测试。

2.1 凹陷模型测试

采用凹陷模型数据对本文方法进行测试, 其中, 图1a是真实的凹陷速度模型, 图1b为本次测试所用的初始模型, 图1c为真实的反射系数模型。模型横纵向采样点为1 801× 301, 横纵向网格间隔均为10 m, 震源为主频30 Hz的雷克子波, 共150炮, 炮间距为10 m, 第一炮坐标为(200 m, 10 m), 每炮检波器个数为1 800 个, 检波器间隔为10 m, 时间采样为6.0 s, 时间采样间隔为0.5 ms, 分别采用常规偏移(高斯束偏移)和本文方法对其成像。

图1 凹陷速度模型
a— 真实速度模型; b— 初始速度模型; c— 反射系数模型

图2a和图2b分别是用常规偏移(高斯束偏移)和本文方法迭代30次的成像结果。对比图2a和图2b可以发现, 本文方法提高了成像剖面振幅的均衡性, 同时, 本文方法在常规偏移不能成像的区域进行了准确的成像, 说明本方法具有很好的适用性。

图2 常规偏移(上)与本文方法迭代30次(下)的成像结果

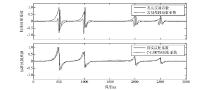
图3是常规偏移与本文方法成像结果的单道(第900道)标准反射系数振幅对比, 其中, 实线表示真实反射系数, 图3b下图虚线表示本文方法的结果, 图3a虚线表示常规偏移结果。可以看出, 本文方法与真实反射系数振幅更加接近, 保幅性更好。

图3 常规偏移(上)与本文方法迭代30次(下)的单道标准反射系数对比

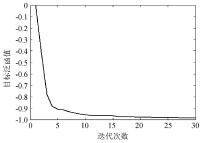
图4是本文方法在对凹陷模型进行测试时的误差泛函收敛曲线, 说明本文方法稳定性很好, 随着迭代次数的增大, 成像精度越来越高。

图4 凹陷模型本文方法泛函收敛曲线

2.2 复杂salt模型测试

采用如图5a所示的salt模型数据测试本文方法的有效性及稳定性, 该盐丘模型中有几组明显的高陡断层。图5b为本次测试所用的初始模型, 图5c为真实的反射系数模型。模型横纵向采样点为645× 150, 横纵向网格间隔均为10 m, 震源为主频30 Hz的雷克子波, 共60炮, 炮间距为10 m, 第一炮坐标为(200 m, 10 m), 每炮检波器个数为600个, 检波器间隔为10 m, 时间采样为6.0 s, 时间采样间隔为0.5 ms, 分别采用常规偏移(逆时偏移)和本文方法对其成像。

图5 salt速度模型
a— 真实速度模型; b— 初始速度模型; c— 反射系数模型

图6a和图6b分别是用常规偏移(逆时偏移)和本文方法迭代30次的成像结果。对比图6a和图6b可以发现, 本文方法提高了成像结果振幅的均衡性, 提高了成像剖面的分辨率, 压制了偏移噪声, 说明本方法具有很好的适用性。

图6 常规偏移(左)与本文方法迭代30次(右)的成像结果

图7是常规偏移与本文方法成像结果的单道(第100道)标准反射系数振幅对比, 其中, 实线表示真实反射系数, 图7b虚线表示本文方法的结果, 图7a虚线表示常规偏移结果。可以看出, 本文方法与真实反射系数振幅吻合的更好, 更具保幅性。

图7 常规偏移(上)与本文方法迭代30次(下)的单道标准反射系数对比

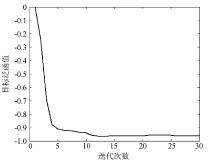
图8是本文方法在对凹陷模型进行测试时的误差泛函收敛曲线, 说明本文方法稳定性很好, 随着迭代次数的增大, 误差泛函稳步收敛, 成像精度越来越高。

图8 复杂salt模型本文方法泛函收敛曲线

3 结论

分析了常规最小二乘逆时偏移成像存在的问题, 将波形反演中的相关泛函引入到最小二乘逆时偏移中, 分别从互相关误差泛函的构建、逆时反偏移数据重构、梯度预条件处理、共轭梯度法迭代求解等方面进行研究, 实现了基于相位匹配的最小二乘逆时偏移成像方法。简单凹陷模型和复杂salt模型测试结果说明了本文方法的有效性和适应性。与常规的偏移成像方法相比, 本文方法在一定程度上能够压制偏移假象, 提高成像结果的保真性和分辨率, 更有利于后续的岩性储层成像。

The authors have declared that no competing interests exist.

参考文献
[1] Baysal E, Dan D K, Sherwood J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. [本文引用:1]
[2] Zhang Y, Zhang H. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011, 76(3): WA3-WA11. [本文引用:1]
[3] 周学明, 李庆春, 马婷. 弹性波叠前逆时偏移[J]. 物探与化探, 2013, 37(2): 274-279. [本文引用:1]
[4] 张慧宇, 王立歆, 孔祥宁, 等. 适于大规模数据的逆时偏移实现方案[J]. 物探与化探, 2015, 39(5): 978-984. [本文引用:1]
[5] Zhang Y, Sun J. Practical issues of reverse time migration: True amplitude gathers, noise removal and harmonic-source encoding[J]. First Break, 2009, 26: 29-35. [本文引用:1]
[6] Xu S, Zhang Y, Tang B. 3D angle gathers from reverse time migration [J]. Geophysics, 2011, 76(2): S77-S92. [本文引用:1]
[7] LeBras R, Clayton R W. An iterative inversion of back-scattered acoustic waves[J]. Geophysics, 1988, 53(4): 501-508. [本文引用:1]
[8] Dai W, Boonyasiriwat C, Schuster G. 3D multi-source least squares reverse time migration [C] //79thAnnual International Meeting, SEG, Expand ed Abstracts, 2009: 3120-3124. [本文引用:1]
[9] Dai W, Schuster G T. Multi-source wave equation least squares migration with a deblurring filter[C]//Expand ed Abstracts of 72nd EAGE Conference & Exhibition Incorporation SPE Europec, 2010, 276-281. [本文引用:1]
[10] Wong M, Ronen S, Biondi B. Least-squares reverse time migration/inversion for ocean bottom data: A case study[C]//81stAnnual International Meeting, SEG, Expand ed Abstracts, 2011: 2369-2373. [本文引用:1]
[11] Dai W, Schuster G T. Plane-wave least-squares reverse-time migration[J]. Geophysics, 2013, 78(4): S165-S177. [本文引用:1]
[12] Dutta G, Schuster G T. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation[J]. Geophysics, 2014, 79(6): S251-S262. [本文引用:1]
[13] 黄建平, 曹晓莉, 李振春, 等. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 2014, 49(1): 107-112. [本文引用:1]
[14] 郭书娟, 马方正, 段心标, 等. 最小二乘逆时偏移成像方法的实现与应用研究[J]. 石油物探, 2015, 54(3): 301-308. [本文引用:1]
[15] Lin Y L, Huang L. Least-squares reverse-time migration with modified total-variation regularization[C]//85thAnnual International Meeting, SEG, Expand ed Abstracts, 2015: 4264-4269. [本文引用:1]
[16] Dong S, Cai J, Guo M, et al. Least squares reverse time migration: Towards true amplitude imaging and improving the resolution[C]//82ndAnnual International Meeting, SEG, Expand ed Abstracts, 2012: 1425-1429. [本文引用:1]
[17] Yao G, Jakubowicz H. Least-squares reverse-time migration[C]//82ndAnnual International Meeting, SEG, Expand ed Abstracts, 2012: 3406-3410. [本文引用:1]
[18] Zeng C, Dong S Q, Wu Z H, et al. Adaptive least-squares RTM and application to Freedom WAZ subsalt imaging[C]//SEG Technical Program Expand ed Abstracts, 2015: 4059-4064. [本文引用:1]
[19] Zhang Yu, Duan Lian, Xie Yi. A stable and practical implementation of least-squares reverse time migration[C]//SEG Technical Program Expand ed Abstracts, 2013: 3716-3720. [本文引用:1]
[20] Dutta G. A cross-correlation objective function for least-squares migration and visco-acoustic imaging[C]//SEG Technical Program Expand ed Abstracts, 2014: 5183. [本文引用:1]
[21] Zhang Yu, Duan Lian. Predicting multiples using a reverse time demigration[C]//SEG Technical Program Expand ed Abstracts, 2012: 4601-4609. [本文引用:1]
[22] Aoki N, Schuster G. Fast least-squares migration with a deblurring filter [J]. Geophysics, 2009, 74(6): WCA83-WCA93. [本文引用:1]
[23] 陈生昌, 马在田, 吴如山. 波动方程双程地下方向照明分析[J]. 同济大学学报: 自然科学版, 2007, 35(5): 681-684. [本文引用:1]