由于SA和GA产生的随机点有可能被摒弃, 因此大大降低了计算效率。为了解决这一问题, Sambridge^[13]在1999年提出NA算法, 并将其应用于地球物理反演中。该方法的主要思想是将参数空间构造为一个个小的Voronoi单元^[14], 并对最邻近的区域定义合适的距离(通常取L₂范数)。Voronoi单元的公式定义如下:假设P={m₁, …, mnp}为d维空间中互不重复的点集, 其中2≤ n_p≤ ∞ , 则点m_i对应的Voronoi单元为

V(mi)=x‖x-mi≤x-mj; i, j=1, …, np, 且i≠j

图1显示了平面上分别由10、100、1 000个不规则分布的点集所形成的Voronoi单元集。

图1

	Figure Option ViewDownloadNew Window
	图1 不同Voronoi单元数所生成的Voronoi[13] a— 10个均匀随机分布点的初始模型; b— 由Gibbs采样后100个Voronoi单元所结成的空间; c— 1000个Voronoi单元所结成的空间; d— 实际目标函数的等值图

由于所有采样点的误差函数值已知, 可直接将整个Voronoi单元的误差函数近似为该单元内对应采样点的误差值(邻域近似)。因此, 为寻找极小值, 只需要在误差函数相对较小的邻域内按给定算法产生新的采样点即可。Sambridge^[13]指出将Voronoi单元应用于SA和GA中, 可以大大减少正演的次数, 从而提高算法的效率。NA算法在单元内部采用概率为均匀分布的随机行走的方式来产生新的采样点。该算法主要步骤如下:

1) 在参数空间中均匀随机产生n_s个初始模型;

2) 在最近产生的n_s个模型中选择误差函数最小的n_r个模型;

3) 在所选定的n_r个模型所在Voronoi单元中运用均匀同分布随机行走生成n_s个模型(例如:每个单元产生n_s/n_r个模型);

4) 返回步骤2。

如图2所示, 单元内部均匀分布的随机行走可由吉布斯采样得到。设当前模型m_A对应的单元V_k第i个分量方向上与邻近单元V_j、V_l交点分别为m_j、m_l, 对应的i分量为x_j、x_l, 边界为(l_i, u_i)。利用在(x_j, x_l)内采用均匀概率分布产生的值替换m_A中的i分量值, 从而产生新的点m_B。之后以m_B为起点, 对i+1个分量进行类似操作。经过所有d个坐标轴的循环, 产生新的模型, 该模型满足在单元内部为概率均匀分布。从图1中可以看出, 随着采样点的增加, 它越来越接近原来多维空间中的误差函数。

图2

	Figure Option ViewDownloadNew Window
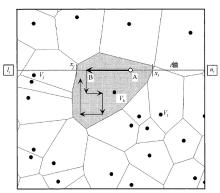	图2 在Voronoi单元内进行均匀分布的随机行走[13] (在单元Vk外条件概率密度设为0, 内部为均匀分布)

当某些物理参数(如温度、密度等)只可能取正值时, 它们的非信息概率密度分布常为对数均匀概率密度分布, 这些参数称为Jeffreys参数。ρ 、d这两个参数可以看作Jeffreys参数, 并且为了能使参数具有较大的变化范围, 在NA反演时参数选取为 m=(logρ1, logρ2, …, logρn, logd1, …, logdn-1);式中ρ _i为第i层的电阻率, d_i为第i层的深度, n为层数。一般岩石电阻率为10^-1~10⁵ Ω · m, 因此不失一般性, 将参数m的范围限定为[0, 5]。

测深曲线可以表示在对数坐标系中, 曲线形态反应的是视电阻率对数随频率的变化, 而不是视电阻率本身, 这样可以更明显地反映电阻率随频率的变化。为了充分利用视电阻率和相位数据, 误差函数应该为两者的联合。参照Jones和Hutton^[15], 研究选取的误差函数为

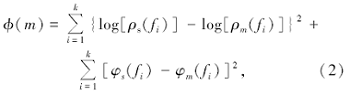
式中:ρ _m、φ _m为在给定参数m下理论视电阻率和相位, ρ _s、φ _s为观测得到的视电阻率和相位, f为选取的频率, k为采样频率的个数。

采用三层地电模型m=[log(ρ ₁), log(ρ ₂), log(ρ ₃), log(d₁), log(d₂)], 理论模型为K型, 参数取为m^* =(1.5, 3.0, 2.5, 2.0, 3.5), 即从第一层到第三层电阻率分别为31.6、1 000.0、316.2 Ω · m, 第一层和第二层的深度分别为100.0、3 162.3 m。采用一维正演公式计算了从10^-4~10⁴ Hz成对数分布等间距的20个频率点f所对位的视电阻率ρ _s和视相位φ _s, 生成的数据无噪声(图3)。

图3

	Figure Option ViewDownloadNew Window
	图3 模型m* 所计算得到的视电阻率曲线(a)和视相位曲线(b)

之后, 采用NA方法计算误差函数ϕ (m), 其中参数设置为n_s=50, n_r=20, 经过20次迭代后, 得到结果如图4所示。可以看出, 反演后 ϕ (m)的最小值(简称最大似然值)为 3.44× 10^-13, 其对应的模型(最大似然模型)为m=(1.52.02, 3.42), 即第一层到第三层电阻率分别为32.4、1 148.2、316.2 Ω · m, 第一层和第二层的深度分别为104.7、2 630.3 m, 与理论模型m^* 符合得很好。

图4

	Figure Option ViewDownloadNew Window
	图4 NA反演生成的点在各个变量上的投影 “ +” 表示最大似然点的位置; “ × ” 表示理论模型值

为了对比NA与GA反演两种方法的收敛效果, 进行了400次NA反演, 反演条件除迭代次数改为100次之外, 与图4所设参数一致, 每次取其最大似然模型, 最后得到图5。这里将迭代次数设为100主要是为了保证最后得出的最大似然点充分收敛至局部极小值。之后又进行了400次GA反演。这里GA的初代种群数目与子代种群数目均取50, 迭代次数同样也为100次, 每次取其最大似然值(图6)。

图5

	Figure Option ViewDownloadNew Window
	图5 400次NA反演所得最大似然值所成的散点 “ × ” 表示理论模型值

图6

	Figure Option ViewDownloadNew Window
	图6 400次GA反演所得最大似然值所成的散点 “ × ” 表示理论模型值

图5、图6表明NA与GA的最大似然值分布十分相似, 只不过相比图6b, 图5b右下方有散点分布, 这是与NA参数n_r与GA相应“ 选择、交叉、变异” 相关参数设置有关。总体来说, 这两种方法抗陷入局部极小值的能力大体相当。不失一般性, 接下来只分析NA的最大似然值分布情况。从图5中可以看出, NA反演并不总是收敛于理论模型m^* , 同样也有可能陷入局部极小值, 这主要反应的是一维MT模型的高度非线性, 同时与采样频率的选取也有一定的关系。从图3可以明显看出采样数据对m₃有很强的约束, 对m₁也有一定的约束, 而对其他参数约束不强, 从而造成图5a、5c均呈直线分布。图5b倾斜的线段与水平线段分别反应了S等值和H等值这两大特性。图4中采样点密度与图5大致相同, 这也说明NA算法生成的点图分布也与误差函数一致, 而GA反演却不具有这种性质。因此, 在NA生成的采样点的基础上利用在贝叶斯框架下的蒙特卡罗积分(MCB)^[8]或邻近算法下的积分(NAB)^[16], 可以得到比GA法更好的模型参数中心估计值及其协方差矩阵。

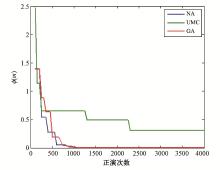
对于全局算法而言, 收敛速度越快, 其所需的正演次数就越小, 这样能够大大减少正演的计算量。在收敛速度分析过程中, 利用UMC算法直接生成不同的模型, 在NA和GA反演时初始参数不变, 反演过程中保证其收敛到理论值的情况下不断改变其迭代次数, 增加反演点, 并计算其最大似然值对应的 ϕ (m), 如图7所示。从图7中可以看到在UMC法的ϕ (m)值始终比NA和GA要大。在生成1 000个点以前NA要比GA的ϕ (m)值要小, 之后两者的ϕ (m)相接近。这说明NA的收敛速度在较小迭代次数下比GA更快。

图7

	Figure Option ViewDownloadNew Window
	图7 正演次数与误差函数的关系

大地电磁法在地质构造探测和矿产勘查等领域应用广泛, 这也对反演提出了更高的要求。目前常见的反演方法多为迭代法, 十分依赖初始模型的选择, 容易陷入局部极小值。而像UMC、SA、GA法等这类全局优化的算法, 虽然不易陷入局部极小值, 但计算量大且对参数设置极为敏感, 收敛较慢。笔者采用的NA算法只需要两个参数n_s、n_r, 概念简单、适用范围广且收敛快。通过对K型三层地电模型的分析, 可以看出NA在一维MT反演的结果与初始结果几乎相同。与GA的最大似然值分布比较表明NA与GA抗陷入局部极小值的能力大致相同, 主要受一维MT模型与采样数据的影响; 同时还表明NA生成的点图分布密度与误差函数ϕ (m)的大小一致, 便于利用贝叶斯估计方法。相比UMC和GA算法, NA的收敛速度更快。在今后的研究中, 有望将NA法推广到更高维的MT反演中。