一种预测天然气饱和度的新方法

引用本文

杨东升, 刘春成, 曹思远, 黄饶. 一种预测天然气饱和度的新方法[J]. 物探与化探, 2016,40(5): 968-973.
YANG Dong-Sheng, LIU Chun-Cheng, CAO Si-Yuan, HUANG Rao. A new method for prediction of gas saturation[J]. Geophysical and Geochemical Exploration, 2016,40(5): 968-973.
Doi:10.11720/wtyht.2016.5.20 复制到剪切板

Permissions

一种预测天然气饱和度的新方法

杨东升¹, 刘春成¹, 曹思远², 黄饶¹

1.中海油研究总院,北京 100028

2.中国石油大学(北京) CNPC物探重点实验室, 北京 102200

作者简介: 杨东升(1983-),男, 工程师,2009年在中国石油大学(北京)获硕士学位,主要从事石油勘探综合研究工作。E-mail:yangdsh@cnooc.com.cn

收稿日期: 2016-01-04

基金: 国家科技重大专项(2016ZX05026-001,2016ZX05026-007)

摘要

先前^[1]介绍了一种基于叠前地震资料预测天然气饱和度的线性岩石物理属性变换的 NI反演方法,并对反演结果进行敏感性分析进而有效预测有商业开采价值的天然气藏。在此基础上通过提高岩石物理属性变换的精度和加强孔隙流体变换约束进一步改进反演算法,有效提高了 NI反演的精度。实际应用结果表明,二次方程 NI反演方法有效提高了复杂地区天然气饱和度的预测效果。

关键词: AVO技术; 岩石物理属性变换; 天然气饱和度; 孔隙流体变换; NI反演

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)05-0968-06 doi: 10.11720/wtyht.2016.5.20

A new method for prediction of gas saturation

YANG Dong-Sheng¹, LIU Chun-Cheng¹, CAO Si-Yuan², HUANG Rao¹

1.CNOOC Research Institute,Beijing 100028,China

2.CNPC Geophysical Key Laboratory,China Petroleum University,Beijing 102200,China

Abstract

A NI inversion method of linear rock physical properties transformation was introduced in previous studies,which can be used to predict gas saturation on the basis of prestack seismic data.The problem as to how to make the sensitivity analysis of the inversion results in order to correctly predict commercial gas reservoirs was discussed.By increasing the rock physical properties transform precision and strengthening the constraint of pore fluid transformation the authors further improved the inversion algorithm,which raises the accuracy of inversion effectively.The practical application results show that the quadratic equation NI inversion method can effectively predict the gas saturation in complex area.

Keyword: AVO technology; rock physicalproperty transforms; gas saturation; pore fluid transformation; NI inversion

Show Figures

天然气饱和度的预测在油气藏评价中是一项非常重要的参数, 同时也是当今工业界和学术界研究的难题。近几年来, 在以Gassmann方程为代表的岩石物理理论研究方面有很大的进展。利用岩石物理技术可以提供各种对储层识别及含油气性分析的敏感岩石物理参数, 有效指导储层预测^[2]。随着国内外地球物理勘探新技术的发展, 很多学者在这方面做了大量有意义的研究工作^{[3, 4, 5, 6, 7]}。刘洋^[8]提出了联合利用纵波速度与纵、横波速度比值计算孔隙度和饱和度的一种新方法。金龙等^[9]提出基于岩石物理模型与混合优化算法定量反演孔隙度和饱和度的方法。巴晶等^[10]研究了非均质天然气藏的岩石物理模型及含气饱和度反演, 反演结果与各井实际的产气情况吻合。Zimmerman C J^[11]利用地震炮检距做AVO分析来识别含气或含水地层。以上研究对烃类检测有一定的效果, 但是仍然无法区分低饱和度含气储层和有商业开采价值的富集气藏, 因为低饱和度天然气与高饱和度天然气对储层的纵波速度有同样的影响 ^[12]。

通常以孔隙空间天然气百分含量的大小, 可将含气储层划分成两类, 当孔隙空间的天然气百分含量小于等于25%时该储层为低饱含气储层(Fizz), 孔隙空间的天然气百分含量大于25%时该储层为饱含气储层(Gas)^[13]。不同孔隙度的储层, 饱含气储层和低饱含气储层有着相似的AVO响应特征^[1]。

针对低饱含气储层和饱含气储层具有相似的AVO响应特征, 利用现有的反演方法很难进行识别和预测这一现状。在研究从地震和岩石物理属性趋势估算含水饱和度的过程中, Zhou等^[14]采用通过对比低倾部位含水的天然气储层和探区的AVO响应来分析预测天然气饱和度的思路, 杨东升等^[1]在此基础上建立一系列正演模型, 对正演模型结果参数进行稳定性分析并探寻能识别含气饱和度的敏感参数, 通过引入两个岩石物理属性变换建立了基于叠前地震资料预测天然气饱和度的线性变换NI(normal incidence reflection coefficient)反演方法, 该方法能有效识别低饱含气储层和饱含气储层。然而, 该方法在复杂地区的识别效果和精度受到制约, 在此基础上, 笔者通过提高岩石物理属性变换的精度并加强孔隙流体变换的约束推导出新的适用于复杂地区天然气饱和度预测的反演方法。

1 高精度岩石物理属性变换

图1分别建立了含水(Wet)、低饱含气储层(Fizz:含水饱和度S_w=90%)、饱含气储层(Gas:S_w=30%)3种地震响应模型, 图1a是基于井模型的AVO地震响应, 图1b是基于该井泥岩的速度和密度增加20%新模型的AVO地震响应, 3个AVO地震响应特征极其相似, 实际仅图1b第3个地震响应结果是饱含气储层。因此, 当储层的孔隙度发生变化时, 其CMP道集非常相似, 单纯从地震响应特征上很难识别出低饱含气储层和饱含气储层。

	Figure Option View Download New Window
	图1 井模型岩石物理属性改变前后的AVO地震响应对比 a— 基于井模型的AVO地震响应; b— 图a井模型基础上泥岩的速度和密度增加20%后新模型的AVO地震响应

因此, 在实际地震资料中低饱含气储层和饱含气储层很难被识别。用天然气饱和度的线性变换NI反演方法中提供的辨别思路, 利用下倾部位不同含水饱和度地层AVO响应的差异性来协助识别低饱含气储层和饱含气储层^[1]。根据区域趋势得到的标准偏差值建8类岩石物理属性变差模型, 分别是:①将泥岩的密度和速度增加1个标准偏差值; ②将泥岩的密度和速度减少1个标准偏差值; ③将砂岩的密度和速度增加1个标准偏差值; ④将砂岩的密度和速度减少1个标准偏差值; ⑤同时将砂岩和泥岩的密度和速度增加1个标准偏差值; ⑥同时将砂岩和泥岩的密度和速度减少1个标准偏差值; ⑦将砂岩属性增加0.5个偏差值并将泥岩属性减小0.5个偏差值; ⑧将泥岩属性增加0.5个偏差值并将砂岩属性减小0.5个偏差值。并对模型AVO响应结果进行稳定性分析, 得出含烃类储层的法向入射反射系数NI_h与含水砂岩的法向入射反射系数NI_w之差, 即Δ NI=NI_h-NI_w属性对岩石物理属性变化不是很敏感的结论, 也就是通过模型建立了该区域低饱含气储层和饱含气储层的识别量板, 当Δ NI≥ -0.05, 为低饱含气储层, 如果小于Δ NI< -0.05, 则为饱含气储层(图2)。因此, 如果能够从地震中更精确地反演出流体的法向入射反射系数属性参数, 就能通过有效的模型分析来预测出饱含气储层^[1]。

	Figure Option View Download New Window
	图2 模型的稳定性分析^[1] 横轴0为原始模型, 1~8分别为8类偏差模型(图5~7同)

从地震中反演出各流体更精确的NI参数, 就需要量化不同的地震振幅。同样引入孔隙流体变换和岩石物理属性变换, 孔隙流体变换是含水砂层的法向入射反射系数NI_w和含烃类法向入射反射系数NI_h相关的变换; 岩石物理属性变换是不同饱和度下孔隙流体的法向入射反射系数NI和30° 角入射时的反射系数R_C(30° )的相关变换。该方法的思路就是预测探区含烃类法向入射反射系数NI_h, 然后利用含烃类法向入射反射系数NI_h和低倾部位含水储层法向入射反射系数NI_w之差Δ NI=NI_h-NI_w属性来识别饱含气储层。因此, 反演出各流体更精确的法向入射反射系数NI参数将有助于提高该方法在复杂地区的实际应用效果, 根据反演算法推导过程分析, 提高岩石物理属性变换的精度并加强孔隙流体变换的约束将有助于提高复杂地区天然气饱和度的预测效果。

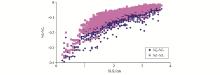
以下根据MG地区岩石物理属性模型试验数据绘制的含烃和含水的法向入射反射系数NI图(如图3), 并且通过二次方程拟合关系式来获取 “ 区域约束方程” 。

	Figure Option View Download New Window
	图3 二次方程孔隙流体变换

同理, 可绘制不同流体入射角为30° 时的反射系数和法向入射反射系数的二次方程相关图(图4), 其二次方程相关的系数见表1。

	Figure Option View Download New Window
	图4 二次方程岩性变换

表1 二次方程岩性变换的系数

2 含水饱和度的地震反演新方法

1993年, Lin和Phair将薄层的振幅近似定义为^[15]:

$\begin{matrix} A (θ) = k \times \frac{4 πb}{vT} \times R_{C} (θ) \times \cos (θ), (1) \end{matrix}$

其中:k是一个常数; b是岩床厚度, m; θ 是入射角, (° ); A(θ )是薄层地震振幅; R_C(θ )是上层边界的反射系数; v是薄层的层速度, m/s; T是子波周期, s。对一个地区同一个地震测网来说, k和T被视为常数值。通过岩性变换将表达式k× $\begin{matrix} \frac{4 πb}{vT} \end{matrix}$ 替换掉。

通过线性岩性变换可推导出线性变换NI反演方程^[1] :

$\begin{matrix} NI = R_{C} (0 °) = \frac{A (0 °)}{k \times \frac{4 πb}{vT}} = \frac{L_{2} \times A (0 °)}{\frac{A (30 °)}{\cos (30 °)} - L_{1} \times A (0 °)}, (2) \end{matrix}$

A(0° )和A(30° )是从实际CDP道集中表征地震振幅的项, 不同的流体饱和度就有不同的L₁, L₂值。因此, 使用从低倾的CDP道集以及表1中“ Wet” 的系数获得的远近道振幅能够估算出NI_w, 通过孔隙流体变换的约束方程利用反演出的含水储层法向入射反射系数NI_w结果来求取饱含气储层法向入射反射系数NI_g或低饱含气储层法向入射反射系数NI_f。

在复杂的地区, 为了提高含气饱和度的预测精度, 通过二次方程来拟合孔隙流体变换和岩石物理属性变换得到高精确岩石物理属性变换方程。拟合的高精度岩石物理属性变换方程可以写为:

$\begin{matrix} R_{C} (30 °) = c_{0} - c_{1} NI + c_{2} N I^{2} 。 (3) \end{matrix}$

当θ 分别等于30° 和0° 时, 利用式(3)及式(1)的方程可以推出一个更精确的反演表达式:

$\begin{matrix} NI = \frac{\{[\frac{A (30 °)}{\cos (30 °)} - c_{1} \times A (0 °)] + M\}}{[2× A (0 °) \times c_{2}]}, (4) \end{matrix}$

其中:

$\begin{matrix} M = \sqrt{\{{[\frac{A (30 °)}{\cos (30 °)} - c_{1} A (0 °)]}^{2} - 4 c_{0} c_{2} A^{2} (0 °)\}} 。 (5) \end{matrix}$

线性岩石物理属性变换的含水饱和度NI反演称为线性变换NI反演^[1]; 将改进后的新反演算法称为二次方程变换NI反演。

3 敏感度分析

分别应用式(2)的线性变换NI反演与式(4)的二次方程变换NI反演来求取各流体模型的NI_w, NI_g和NI_f值; 然后分别计算线性孔隙流体变换约束下与二次方程孔隙流体变换约束下的Δ NI_f=NI_f-NI_w和Δ NI_g=NI_g-NI_w。如果|Δ NI|≥ 0.05, 为饱含气储层; 如果|Δ NI|< 0.05, 则为低饱含气储层。

据图5反演结果, 两种反演方法的Δ NI能有效识别出低饱含气储层和饱含气储层。低饱含气储层的Δ NI分布在0.03~0.05之间, 饱含气储层的Δ NI分布在0.05~0.08之间。因此, 可以利用孔隙流体变换约束下的含水饱和度地震反演来识别低饱含气储层和饱含气储层。

	Figure Option View Download New Window
	图5 两种NI反演的精度对比分析

两种流体状态下(图6和图7)的Δ NI理论值与反演结果的误差分析结果表明改进后的二次方程孔隙流体约束下的NI反演方法误差更小。因此, 改进后的二次方程孔隙流体约束下的反演较线性孔隙流体约束下的NI反演具有更好的稳定性和精确度。

	Figure Option View Download New Window
	图6 饱含气储层中两种NI反演方法的误差对比分析

	Figure Option View Download New Window
	图7 低饱含气储层中两种NI反演方法的误差对比分析

4 含水饱和度反演新方法的应用

根据Dr. Caosy提供的MXG区域叠前数据集进行流体饱和度的评估, 分别应用式(2)的线性变换NI反演与式(4)的二次方程变换NI反演计算NI_w。

在图8和图9为分别应用两种反演算法计算出目标区不同流体的NI值绘制出整个深度范围的NI_h-NI_w, 图9中的二次方程NI变换反演结果的区分效果要明显好于图8线性变换NI反演的区分效果。因此, 实际资料反演结果表明高精度孔隙流体变换约束下的二次方程变换NI反演进一步提高了复杂地区天然气饱和度的预测效果。

	Figure Option View Download New Window
	图8 目标区整个深度范围内的线性变换NI反演结果

	Figure Option View Download New Window
	图9 目标区整个深度范围内的二次方程变换NI反演结果

5 结论

岩石物理属性变换NI反演提供了一个从近、远角叠加振幅提取NI的方法, 通过提高岩石物理属性变换的精度并加强孔隙流体变换的约束推导出新的适用于复杂地区天然气饱和度预测的反演算法。模型反演结果分析表明:高精度孔隙流体变换约束下的二次方程变换NI反演比孔隙流体变换约束下的线性岩石物理属性变换NI反演具有更高的反演精度, 能够估算出更精确的Δ NI值, 进一步提高了该方法的反演效果。实际资料的结果表明, Δ NI属性能有效识别低饱含气储层和饱含气储层, 高精度孔隙流体变换约束下的二次方程变换NI反演进一步提高了复杂地区天然气饱和度的预测效果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨东升, 李绪宣, 曹思远. 天然气饱和度预测方法的研究及应用[J]. 中国海上油气, 2014, 26(1): 39-43. [本文引用:6]
[2]	尚新民, 李红梅, 韩文功, 等. 基于岩石物理与地震正演的AVO分析方法[J]. 天然气工业, 2008, 28(2): 64-66. [本文引用:1]
[3]	邓继新, 王尚旭. 基于统计岩石物理的含气储层饱和度与孔隙度联合反演[J]. 石油天然气学报, 2009, 31(1): 48-54. [本文引用:1]
[4]	李凌高, 王兆宏, 甘利灯, 等. 基于叠前地震反演参数的流体饱和度定量预测方法[J]. 石油物探, 2009, 48(2): 121-125. [本文引用:1]
[5]	宋建国, 王艳香, 乔玉雷, 等. AVO技术进展[J]. 地球物理学进展, 2008, 23(2): 508-514. [本文引用:1]
[6]	时磊, 刘俊州, 董宁, 等. 扩展弹性阻抗反演技术在致密砂岩薄储层含气性预测中的应用[J]. 物探与化探, 2015, 39(2): 346-351. [本文引用:1]
[7]	杨国杰, 宋丽媛, 商建霞. 地质统计反演技术在坨11 南地区储层预测中的应用[J]. 物探与化探, 2015, 39(6): 1193-1198, 1204. [本文引用:1]
[8]	刘洋. 利用地震资料估算孔隙度和饱和度的一种新方法[J]. 石油学报, 2005, 27(4): 61-64. [本文引用:1]
[9]	金龙, 陈小宏, 姜香云. 利用地震资料定量反演孔隙度和饱和度的新方法[J]. 石油学报, 2006, 26(2): 63-66. [本文引用:1]
[10]	巴晶, 晏信飞, 陈志勇, 等. 非均质天然气藏的岩石物理模型及含气饱和度反演[J]. 地球物理学报, 2013, 56(5): 1696-1706. [本文引用:1]
[11]	Zimmerman C J. 用地震炮检距方程(SRE)作AVO分析确定低含气饱和度[J]. 石油物探译丛, 1993, 3: 59-64. [本文引用:1]
[12]	杨东升, 李绪宣, 刘春成, 等. 基于岩石物理与地震正演的天然气饱和度分析[J]. 石油天然气学报, 2013, 35(6): 53-58. [本文引用:1]
[13]	Han D, Baztle M. Fizz water and low gas-saturated reservoirs[J]. The Leading Edge, 2002, 21: 395. [本文引用:1]
[14]	Zhou Z, Hilterman F, Ren H, et al. Water-saturation estimation from seismic and rockproperty trends[C]//75^th Annual International Meeting, SEG, Expand ed Abstracts, 2005: 258-261. [本文引用:1]
[15]	Lin T L, Phair R. AVO Tuning[C]//63^rd Annual International Meeting, SEG, Expand ed Abstracts, 1993: 727-730. [本文引用:1]

2014

0.0

杨东升, 李绪宣, 曹思远. 天然气饱和度预测方法的研究及应用[J]. 中国海上油气, 2014, 26(1): 39-43.

摘　要：基于对AVO技术研究现状的深入调研,重点研究了基于叠前地震资料预测天然气饱和度的线性岩石属性变换的NI反演方法,探讨了如何对反演结果进行敏感性分析来正确预测有商业开采价值的天然气储层。实际应用结果表明,本文提出的天然气饱和度预测方法可行有效。

... 不同孔隙度的储层,饱含气储层和低饱含气储层有着相似的AVO响应特征^[1] ...

... 在研究从地震和岩石物理属性趋势估算含水饱和度的过程中,Zhou等^[14]采用通过对比低倾部位含水的天然气储层和探区的AVO响应来分析预测天然气饱和度的思路,杨东升等^[1]在此基础上建立一系列正演模型,对正演模型结果参数进行稳定性分析并探寻能识别含气饱和度的敏感参数,通过引入两个岩石物理属性变换建立了基于叠前地震资料预测天然气饱和度的线性变换NI(normal incidence reflection coefficient)反演方法,该方法能有效识别低饱含气储层和饱含气储层 ...

... 用天然气饱和度的线性变换NI反演方法中提供的辨别思路,利用下倾部位不同含水饱和度地层AVO响应的差异性来协助识别低饱含气储层和饱含气储层^[1] ...

... 因此,如果能够从地震中更精确地反演出流体的法向入射反射系数属性参数,就能通过有效的模型分析来预测出饱含气储层^[1] ...

... 通过线性岩性变换可推导出线性变换NI反演方程^[1] : ...

... 线性岩石物理属性变换的含水饱和度NI反演称为线性变换NI反演^[1] ...

2008

0.0

尚新民, 李红梅, 韩文功, 等. 基于岩石物理与地震正演的AVO分析方法[J]. 天然气工业, 2008, 28(2): 64-66.

Based on the theory of petrophysics, an approach of Swave velocity estimation from logging data and other related information is developed. In a case study, seismic forward modelling is also carried out to ensure the reflection features of reservoir in the target area. According to the seismic reflection difference between before and after fluids displacement, a criterion for hydrocarbon detection is established, with which we can tell whether the layer contains gas or not. No matter the layer is sand or limestone, the criterion works well in the given examples. It is showed that AVO is an effective method to reveal the influence of porous fluids to seismic data, and the AVO analysis technology based on petrophysics and seismic modelling is relatively reliable and feasible.

以岩石物理理论为基础，根据测井资料和其他相关信息，建立了横波速度的估算方法。以研究区储层为例，进行了地震反射正演模拟，借以研究含气储层的地震反射特征。结果指出，可通过流体替换前后的地震反射差异建立烃类判别准则，并通过AVO分析实现储层含气与否的直接判别。通过对砂岩储层和碳酸盐岩储层的实际应用表明，AVO技术是一种能够反映孔隙流体对地震反射特征影响的有效方法，而建立在岩石物理与地震正演基础上的AVO分析具有更高的可信度和可行性。

... 利用岩石物理技术可以提供各种对储层识别及含油气性分析的敏感岩石物理参数,有效指导储层预测^[2] ...

2009

0.0

邓继新, 王尚旭. 基于统计岩石物理的含气储层饱和度与孔隙度联合反演[J]. 石油天然气学报, 2009, 31(1): 48-54.

从地震数据中得到饱和度与孔隙度等储层物性参数是进行储层评价的关键.利用Gassmann方程讨论了储层岩石骨架特征、孔隙流体特征对介质地震弹性性质的影响,研究结果表明利用地震弹性属性反演饱和度等物性参数有其实现的特定岩石物理基础,其一是在气/水/油多相流体中,气体的体积模量相对于水/油的体积模量具有一定的可比性,而不能被忽略;其二是岩石骨架的纵波阻抗等弹性属性对所赋存孔隙流体的变化较为敏感.这样岩石的纵波阻抗等弹性参数随含水饱和度变化的变化率会明显增大,从而降低了从地震弹性属性中求取饱和度的不确定性和不稳定性.考虑到孔隙度与饱和度对储层岩石弹性特征影响的相关性,给出了基于随机岩石物理模型的Bayesian技术对孔隙度与含水饱和度进行联合反演的方法和步骤,并将该方法运用干高孔隙度含气砂岩储层的孔隙度及含水饱和度的预测中获得了较好的应用效果.

... 随着国内外地球物理勘探新技术的发展,很多学者在这方面做了大量有意义的研究工作^[3,4,5,6,7] ...

2009

0.0

李凌高, 王兆宏, 甘利灯, 等. 基于叠前地震反演参数的流体饱和度定量预测方法[J]. 石油物探, 2009, 48(2): 121-125.

提出了一种基于测井数据和叠前地震反演参数的流体饱和度定量预测方法--孔隙体积模量法.该方法基于Gassmann方程,在假设已经对岩性进行了可靠的定性预测,并较准确地计算了砂岩的泥质含量和孔隙度的前提下,利用测井资料计算干燥岩石体积模量和孔隙体积模量,利用各种叠前反演得到的弹性参数拟合干燥岩石体积模量,建立含水饱和度与孔隙体积模量的关系式,对流体饱和度进行定量估算.利用长庆油田苏里格地区的实际地震资料对孔隙体积模量法进行了验证,结果表明,该方法能定量预测含气饱和度,且能半定量预测气层的产能.根据预测结果部署的井位经钻探获得了高产气流.

... 随着国内外地球物理勘探新技术的发展,很多学者在这方面做了大量有意义的研究工作^[3,4,5,6,7] ...

2008

0.0

宋建国, 王艳香, 乔玉雷, 等. AVO技术进展[J]. 地球物理学进展, 2008, 23(2): 508-514.

AVO technique is an important application of Zoeppritz′s equation in geophysical exploration. After brief reviewing Zoeppritz′s equation and its simplified equations, this paper introduces recent development of AVO technique. AVO technique is a vital tool of utilizing seismic data to explore lithology and hydrocarbon. Modern AVO theory and technique present new aspects such as: using P-wave, S-wave and converted wave AVO analysis of multi-component seismic data to predict gas and detect fracture; using AVO technique to characterize lithology and fluid character quantitatively, to progress 3D AVO analysis, and so on. This paper also prospects the future development of AVO technique.

(1.Faculty of Geo-Resource and Information, China University of Petroleum, Dongying 257061, China2.Shengli Geophysical Research Institute, SINOPEC, Dongying 257060, China)

AVO技术是Zoeppritz方程在地球物理勘探中的重要应用.本文在回顾Zoeppritz方程及其简化形式的基础上对AVO技术的最近发展进行了介绍.AVO技术是利用地震资料研究岩性和含油气性不可或缺的工具.近年来AVO理论和技术发展呈现新的方向，主要表现在以下几个方面：利用多波多分量地震数据进行纵波、横波、转换波的AVO分析，预测储层的含气性和检测裂缝发育；利用AVO技术定量表征岩性和储层的流体性质；进行3D AVO分析研究等.本文对此进行了介绍，并对AVO技术的前景进行了展望.

... 随着国内外地球物理勘探新技术的发展,很多学者在这方面做了大量有意义的研究工作^[3,4,5,6,7] ...

2015

0.0

时磊, 刘俊州, 董宁, 等. 扩展弹性阻抗反演技术在致密砂岩薄储层含气性预测中的应用[J]. 物探与化探, 2015, 39(2): 346-351.

Compared with the post-stack inversion,the extended elastic impedance is more sensitive to the reservoir and hydrocarbon.In this paper,the authors discussed the theory,key techniques and steps of the extended elastic impedance inversion.Wetake P 1 x 1 and P 1 s 2 in DND gas field of North of Erdos Basin were taken as the study objects.Based on a detailed analysis of logging data,the authors propose fusion method for estimating data of shear wave.This method combines modeling method,formula method and neural network method.It estimates the sandstone section using modeling method,and mudstone with formula method for low frequency model and,in combination with neural network,predicts the mudstone section of shear wave information,thus avoiding the error of mudstone caused by total porosity measurement inaccurate prediction using Xu-White model. Based on cross pictures analysis,the authors deal with sensitive elastic parameters for EEI inversion and effective scale for interpretation of lithology and fluid and,according to deterministic extended elastic impedance inversion,determine the variation and range and complete the pre-stack stochastic extended elastic impedance inversion,thus meeting the requirements of thin reservoir prediction.At last,the inversion results are interpreted crossly and the distribution of gas sand is predicted accurately,with the drilling data matching rate reaching over 90%.

与叠后反演相比,叠前弹性阻抗对储层或烃类更为敏感,而扩展弹性阻抗反演是一种利用振幅随偏移距变化来分析、识别岩性和含气性的有效方法技术。笔者论述了扩展弹性阻抗反演方法理论和反演关键技术、步骤,并针对鄂尔多斯盆地北部DND气田盒1、山2段典型致密砂岩气藏的含气预测,提出了一套融合技术思路进行横波估测,该方法将公式法、模型法和神经网络法结合,以便在砂岩段使用模型法估算,在泥岩段以公式法为低频约束,同时结合神经网络法来预测泥岩段横波信息,避免了Xu-White模型由于总孔隙度测量不准确造成的泥岩段预测误差。实际应用表明,该方法能够满足致密砂岩薄储层含气预测,准确地预测了含气砂体的展布情况,预测结果与实钻吻合率高达90%。

... 随着国内外地球物理勘探新技术的发展,很多学者在这方面做了大量有意义的研究工作^[3,4,5,6,7] ...

2015

0.0

杨国杰, 宋丽媛, 商建霞. 地质统计反演技术在坨11 南地区储层预测中的应用[J]. 物探与化探, 2015, 39(6): 1193-1198, 1204.

The prediction of oil-bearing sand of the second member of Eocene Shahejie Formation of Tuo 11 south area faces many problem.First,oil-bearing sand cannot be identified by seismic data because of the small thickness;Second,there exists difference of P-impedance between oil-bearing sand and water-bearing sand.Through the analysis of the geophysical characteristics of oil-bearing sand and water-bearing sand,the authors predicted the spatial distribution characteristics of oil-bearing sand using geostatistical inversion under the constraints of resistivity curve,and also predicted the oil-water interface.Inversion results have confirmed that the oil-water interface is at about the depth of 2237 m,which expands the oil-bearing area determined by early studies and is in good agreement with the results of the new drilling.Geostatistical inversion results have achieved good result in Tuo 11 south area for the first time,which widens the train of thought for the further exploration.

针对坨11南地区沙二段8砂组含油砂体较薄,低于地震资料分辨率,且油砂与水砂纵波阻抗差异较小,有效储层识别难的问题,本次研究在分析油层与水层的地球物理响应特征的基础上,应用地质统计反演技术,并结合电阻率曲线来约束反演,预测出了该区沙二段8砂组含油砂体的空间展布特征,并探索性地预测出了该区油藏的油水界面。反演结果证实:坨11南地区沙二段8砂组油藏的油水界面大约在2237 m,扩大了早期研究确定的含油面积,与新钻井结果吻合较好。地质统计反演结果首次在坨11南地区的探索应用中取得了较好的效果,为该区进一步的勘探拓宽了思路。

... 随着国内外地球物理勘探新技术的发展,很多学者在这方面做了大量有意义的研究工作^[3,4,5,6,7] ...

2005

0.0

刘洋. 利用地震资料估算孔隙度和饱和度的一种新方法[J]. 石油学报, 2005, 27(4): 61-64.

应用Gassmann方程,计算分析了孔隙度和饱和度与纵波速度、横波速度、介质密度和纵、横波速度比值的关系.结果表明,波速度、介质密度对孔隙度的变化较为敏感,速度比值对饱和度的变化较为敏感.对联合利用纵波速度(或纵波波阻抗)与纵、横波速度比值计算孔隙度和饱和度方法的稳定性分析结果表明,此方法是较稳定的,其精度受油气物性的影响.论述了利用地震资料估算孔隙度和饱和度的方法和步骤.

... 刘洋^[8]提出了联合利用纵波速度与纵、横波速度比值计算孔隙度和饱和度的一种新方法 ...

2006

0.0

金龙, 陈小宏, 姜香云. 利用地震资料定量反演孔隙度和饱和度的新方法[J]. 石油学报, 2006, 26(2): 63-66.

提出了一种基于岩石物理模型与混合优化算法同时反演孔隙度和饱和度的新方法.将孔隙度和饱和度的取值范围加入反演过程作为约束,能提高反演的稳定性和精度.基于地震纵、横波速度反演结果,直接得到油藏参数值.该方法也可以推广到直接利用地震振幅属性来进行反演.分析了不同属性组合对孔隙度和饱和度反演结果的影响.模型计算结果表明,该方法具有精度热高、稳定性好等优点,同时易于推广到多种岩石物理模型、多地震属性组合与多参数定量反演中.

... 金龙等^[9]提出基于岩石物理模型与混合优化算法定量反演孔隙度和饱和度的方法 ...

2013

0.0

巴晶, 晏信飞, 陈志勇, 等. 非均质天然气藏的岩石物理模型及含气饱和度反演[J]. 地球物理学报, 2013, 56(5): 1696-1706.

In heterogeneous natural gas reservoirs, generally gas forms countless small "patchy"-like packets embedded in the host matrix of water-saturated rocks. This heterogeneity feature (also called the "patchy-saturation") causes significant velocity dispersion and attenuation phenomena for seismic wave propagation. To build an appropriate rock physics model for the application of fluid identification in carbonate reservoirs, multi-scale theoretical modeling is performed for partially-saturated rocks and the quantitative relations between wave responses in different scales and basic properties of lithology and pore fluids are predicted. This approach of modeling is applied in limestone gas reservoirs of the right bank block of Amu Darya river. A multi-scale rock physics template is presented. Comparisons with experimental data, fine interpretation results of log data and seismic data have proved its validity and applicability. In combination with the methods of post-stack wave-impedance inversion and pre-stack elastic parameter inversion, seismic data is used to estimate rock porosity and gas saturation of the reservoirs. The results of estimate are in good agreement with the production status of the wells.

非均质气藏中,天然气一般呈"斑块状"分布于含水岩石内部,这种非均匀分布特征会导致地震波显著的频散与衰减现象.为发展适用于碳酸盐岩储层中流体检测的岩石物理模型,本文基于Biot-Rayleigh波动方程,实现了对非饱和岩石的多尺度理论建模,预测了不同尺度下波响应与岩性、流体间的定量联系.将此项建模技术应用于阿姆河右岸的灰岩气藏,给出了多尺度的岩石物理学图板.通过与实验数据、测井精细解释结果及地震数据的对比分析,本文论证了图板的正确性与可适用性.结合叠后波阻抗反演与叠前弹性参数反演,基于地震资料进行了储层含气饱和度与孔隙度的反演,反演结果与各井实际的产气情况吻合.

... 巴晶等^[10]研究了非均质天然气藏的岩石物理模型及含气饱和度反演,反演结果与各井实际的产气情况吻合 ...

1993

0.0

Zimmerman C

. 用地震炮检距方程(SRE)作AVO分析确定低含气饱和度[J]. 石油物探译丛, 1993, 3: 59-64.

本文介绍地震炮检距方程在 AVO 模拟中的应用。用这种方法可以识别含气或含水地层,但无法区分低含气饱和度和有经济价值的含气饱和度这一难以解释的地质情况。我们所说的低含气饱和度是指测井资料上没有气显示。含水砂层是不会产生可观的地震振幅的。利用 AVO 分析方法无法区分低饱和度气和有经济价值的富集气藏,是因为少量气的存在与大量的气对岩石纵波速度有同样的影响(Domenico,1976)。

... Zimmerman C J^[11]利用地震炮检距做AVO分析来识别含气或含水地层 ...

2013

0.0

杨东升, 李绪宣, 刘春成, 等. 基于岩石物理与地震正演的天然气饱和度分析[J]. 石油天然气学报, 2013, 35(6): 53-58.

摘　要： AVO正演模型与AVO交会分析在AVO技术中占有十分重要的位置。以岩石物理理论为基础，根据MXG地区测井资料和其他相关信息，通过流体替代分析了不同深度条件下天然气饱和度对岩石属性的影响；并利用地震正演模拟及AVO交会分析技术研究了不同条件下天然气饱和度对地震反射特征的影响。其结论和认识可为利用地震AVO分析储层天然气饱和度提供理论基础。

... 以上研究对烃类检测有一定的效果,但是仍然无法区分低饱和度含气储层和有商业开采价值的富集气藏,因为低饱和度天然气与高饱和度天然气对储层的纵波速度有同样的影响 ^[12] ...

2002

0.0

... 通常以孔隙空间天然气百分含量的大小,可将含气储层划分成两类,当孔隙空间的天然气百分含量小于等于25%时该储层为低饱含气储层(Fizz),孔隙空间的天然气百分含量大于25%时该储层为饱含气储层(Gas)^[13] ...

2005

0.0

1993

0.0

... 2 含水饱和度的地震反演新方法1993年,Lin和Phair将薄层的振幅近似定义为^[15]: ...