基于L-BFGS理论求解复程函方程的地震波复走时计算方法

引用本文

黄兴国, 孙建国, 孙章庆, 王乾龙. 基于L-BFGS理论求解复程函方程的地震波复走时计算方法[J]. 物探与化探, 2016,40(5): 961-967.
HUANG Xing-Guo, SUN Jian-Guo, SUN Zhang-Qing, WANG Qian-Long. A fast algorithm for computing complex traveltime based on L-BFGS method[J]. Geophysical and Geochemical Exploration, 2016,40(5): 961-967.
Doi:10.11720/wtyht.2016.5.19 复制到剪切板

Permissions

基于L-BFGS理论求解复程函方程的地震波复走时计算方法

黄兴国^1,², 孙建国^1,², 孙章庆^1,², 王乾龙^1,²

1.吉林大学地球探测科学与技术学院,吉林长春 130026

2.国土资源部应用地球物理综合解释理论开放实验室—波动理论与成像技术实验室,吉林长春 130026

通讯作者: 孙建国(1956-),男,博士,教授,主要从事地下波动理论与成像技术、地震资料处理方法等方面的教学和研究工作。E-mail:sun_jg@jlu.edu.cn

作者简介: 黄兴国(1990-),男,硕士研究生,主要从事地震波传播理论与成像技术方面的研究工作。E-mail:huangxingguo111@163.com

收稿日期: 2016-02-26

基金: 国家自然科学基金项目(41274120、41404085)

摘要

地震波复走时在处理几何射线理论面临的焦散问题有着重要作用。为了获得一种精度高且更为高效的复走时计算方法,将L-BFGS最优化理论引入分离的复程函方程中用于求取等效虚慢度,直接利用复走时实部、虚部正交的条件为目标函数,减少了梯度矩阵的一次乘积,利用计算梯度的正演部分作为复走时计算部分,得到了一种求解复程函方程的L-BFGS快速推进复走时计算方法。通过对解析法、动力学射线追踪法、高斯牛顿—共轭梯度快速推进法、L-BFGS快速推进法计算结果的精度和效率分析,表明L-BFGS快速推进法在精度和效率上均具有一定的优越性,也能适应在实际应用中的大规模计算需求。

关键词: 复程函方程; 复走时; 快速算法; L-BFGS理论; 快速推进法

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)05-0961-07 doi: 10.11720/wtyht.2016.5.19

A fast algorithm for computing complex traveltime based on L-BFGS method

HUANG Xing-Guo^1,², SUN Jian-Guo^1,², SUN Zhang-Qing^1,², WANG Qian-Long^1,²

1.College for Geoexploration Science and Technology,Jilin University,Changchun 130026

2.Laboratory for Integrated Geophysical Interpretation Theory of the Ministry for Land and Resources of China — Laboratory for Wave Theory and Imaging Technology,Changchun 130026

Abstract

Complex traveltime of seismic wave plays an important role in dealing with caustics with which geometric ray theory faces.To obtain a higher accuracy and a more efficient method for calculating the complex traveltime,the authors introduce the L-BFGS optimization method to calculate the imaginary slowness.In addition,orthogonal condition of the real part and imaginary part of complex traveltime are taken as the objective function,and then a new L-BFGS-FMM method is obtained for computing complex traveltime.The numerical examples demonstrate the effectiveness of L-BFGS-FMM used in this paper.An analysis of accuracy and efficiency of the results obtained by using the analytical method,dynamic ray tracing method,Gauss-Newton-conjugate gradient method and L-BFGS-FMM method shows that the L-BFGS-FMM method introduced in this paper is superior to all the other methods,and hence the method introduced in this paper can meet the large-scale computing requirement in practical applications.

Keyword: complex ekional equation; complex traveltime; fast algorithm; L-BFGS method; fast marching method

Show Figures

模拟地震波传播的几何射线理论在面对介质复杂程度超出其假设条件时会出现焦散、多值等现象。为了处理这些现象, 在上个世纪70年代, Feslen等人^[1]提出了将几何射线理论的相位部分, 实质是对地震波走时, 扩展为复值的一类波来模拟地震波传播, 这类波被称为消散波(evanescent waves)。消散波的波前和波路径互相垂直, 沿着波路径垂直的方向迅速衰减, 也就是以这种垂直于射线方向(波路径方向)的方式到达几何射线不能传播到的焦散区。目前被广泛应用地震波模拟^{[2, 3]}以及地震偏移^{[4, 5]}的高斯波束就是这类消散波的一种。除此之外, 吸收介质中采用的复走时实质也是利用消散波的复走时上述特征。因此, 对复走时计算方法的研究具有理论价值和应用意义。

在复走时计算方面, 由于需要同时计算其实部和虚部两部分, 自动地给求解带来了难度, 因此计算方法大多都停留在理论层面。这其中包含了Felsen^[1]提出的等时面追踪法, 基本思想是首先构建复走时实部、虚部的法线, 然后分别根据射线方向和垂直与射线方向的网格增量来计算复走时。Magnanini和Talenti^[6]提出的二阶非线性方程法, 基本思想是利用数学变换对复走时的实部和虚部进行分离, 分别建立实部和虚部所满足的非线性微分方程。而目前能实际应用的数值解法只有动力学射线追踪法, 也就是目前在高斯波束偏移领域广泛采用的方法。

然而, 动力学射线追踪法的理论基础是二阶Taylor展开, 因此其计算精度受傍轴近似的制约。更为重要的一点是, 这种方法只能顾及在中心射线路径上速度及其二阶导数的变化, 根本没有考虑中心射线附近速度的不均匀性, 因此当中心射线附近区域出现两侧速度不对称, 甚至速度突变时, 计算出的复走时与真实情况相差会很大。

为了克服上述方法的局限性, Li等人^[7]提出了基于复程函方程的扰动法。在这种方法中, 将复走时虚部的梯度绝对值等效为一个新的虚慢度。为了求出这个慢度值, 将复走时虚部、实部梯度正交的条件设为一个目标函数, 然后再利用一个基于高斯牛顿法和共轭梯度法最优法(GN-CG)求出等效虚慢度, 最后利用快速推进法^[8]计算复走时; Huang等人^[9]在此基础上通过引入不等距有限差分处理波的非规则边界发展了局部复走时算法, 由于该算法仅计算离波束中心射线较近部分的复走时, 限制了计算范围, 因此降低了计算量。

笔者的目的是寻找一种精确和快速的最优化方法求取虚慢度值, 从而能满足实际应用的大尺度复走时计算要求。为此, 引入有限内存-Broyden-Fletcher-Goldfarb-Shanno(L-BFGS)方法。L-BFGS方法基本思想起源于Perry的研究^[10], Nocedal^[11], Liu和Nocedal^[12]对其进行了发展。该方法是对基本的牛顿迭代法Hessian矩阵进行修正的拟牛顿迭代法的一种, 其基本思想是利用当前迭代的曲率信息来构建Hessian矩阵, 将一个n× n的矩阵分解为很少的几个长度为n的矢量, 因此在计算时节省计算机内存, 从而能适用于更大尺度计算。

上述引入L-BFGS方法是对算法求取虚慢度的关键一步进行改进。为了能降低计算量, 直接利用复走时实部、虚部梯度正交的条件为目标函数, 如此减少了梯度计算时的一个矩阵乘积。另一方面, 对算法的整体实现步骤进行了修改, 即将迭代过程中梯度计算时的正演部分视为复走时计算部分, 当迭代终止时, 复走时计算便完成。

在下文中, 首先了介绍了复程函方程的基本理论, 然后建立了求解虚慢度的目标函数, 介绍了L-BFGS方法与计算步骤, 并对基于扰动理论的目标函数梯度导出过程进行了回顾, 除此之外, 对算法的整体实现步骤进行了描述, 最后通过精度和效率分析证实了本文计算方法的优越性, 并通过计算实例验证了本文算法面对复杂介质的稳定性和适用性。

1 复程函方程

地震波实走时可以通过数值求解实程函方程^[13]

$\begin{matrix} \nabla \tilde{τ} (r) \cdot \nabla \tilde{τ} (r) = \frac{1}{v^{2} (r)} = p^{2} (r) (1) \end{matrix}$

得到。其中, p(r)=1/v(r)是介质的慢度, $\begin{matrix} \tilde{τ} \end{matrix}$ (r)是实走时。为了得到复走时, 需将 $\begin{matrix} \tilde{τ} \end{matrix}$ (r)表示为复数形式, 其实部和虚部分别为 $\begin{matrix} {\tilde{τ}}_{R} \end{matrix}$ (r)和 $\begin{matrix} {\tilde{τ}}_{I} \end{matrix}$ (r), 即

$\begin{matrix} \tilde{τ} (r) = {\tilde{τ}}_{R} (r) + i {\tilde{τ}}_{I} (r) (2) \end{matrix}$

为了简便, 在后文的叙述中, 我们省略r。将方程(2)代入式(1)中, 并进行实部、虚部分离, 得到^[14]

$\begin{matrix} \begin{matrix} \nabla^{2} {\tilde{τ}}_{R} - \nabla^{2} {\tilde{τ}}_{I} = p^{2}, (3) \\ \nabla {\tilde{τ}}_{R} \cdot \nabla {\tilde{τ}}_{I} = 0 。 (4) \end{matrix} \end{matrix}$

上述方程组即为分离后的复程函方程。其中, 方程(4)意味复走时实部、虚部正交。

由于方程(3)同时包含了复走时实部、虚部两个未知参数, 给数值求解带来了困难, 所以引入一个虚慢度w, 将其分解为^[7]:

$\begin{matrix} \begin{matrix} |\nabla τ_{I} |^{2} = w^{2}, (5) \\ |\nabla τ_{R} |^{2} = p^{2} + w^{2} 。 (6) \end{matrix} \end{matrix}$

如此, 方程(4)、(5)、(6)共同组成了复程函方程的替代形式, 后文中的地震波复走时计算方法就是以这三个方程为基础建立的。

2 目标函数与梯度

根据上文中的叙述, ∇ $\begin{matrix} {\tilde{τ}}_{R} \end{matrix}$ · ∇ $\begin{matrix} {\tilde{τ}}_{I} \end{matrix}$ =0意味着复走时刻画的地震波传播到的任意位置其走时实部、虚部是梯度正交的, 但由于实际计算出的复走时并非绝对精确, 即不能完全满足走时实部、虚部梯度正交的条件。而复走时和慢度存在着必然的联系, 这种联系在这里体现为一种隐示关系。既然是一种隐示关系, 则无法直接通过该条件求取虚慢度, 因此, 利用反演的思想以复走时实部、虚部的梯度的点积为目标函数, 迭代优化使其达到最小来求取虚慢度。

令目标函数

$\begin{matrix} f = \nabla {\tilde{τ}}_{R} \cdot \nabla {\tilde{τ}}_{I}, (7) \end{matrix}$

目标函数为以上形式的原因在于文中运用拟牛顿方法(L-BFGS)进行求解, 这种方法的优点是在迭代过程中利用了目标函数的二次偏导数, 而且能降低内存使用量和提高计算效率, 从而提高整个算法的效率。本文算法的目标函数与Li等^[7]的高斯牛顿— 共轭梯度法中的目标函数不同, 原因是高斯牛顿法要求目标函数为非线性最小二乘形式, 本文的算法则没有这一要求。另外, 为了简便, 后文中的叙述我们忽略公式中的波浪线。

根据上文中的叙述, 目标函数与虚慢度是一种隐示关系, 因此不能直接建立该目标函数的导数。为此, 引用Li等人^[7]通过扰动理论思想间接地建立目标函数的导数公式:

$\begin{matrix} \nabla_{w} f (w_{0}) = [L_{R} L_{I}^{- 1} + L_{I} L_{R}^{- 1}] w_{0}, (8) \end{matrix}$

计算梯度值时要依赖于上一次迭代计算出的w值和初始w₀的值。

3 L-BFGS理论

本节的目的是建立一种能用于实际应用的大尺度和更为快速的求解慢度w的计算方法。为了达到这一目的, 首先, 将Newton理论应用于方程(7), 得到:

$\begin{matrix} \nabla_{w}^{2} f (w) Δw = - \nabla_{w} f (w) 。 (9) \end{matrix}$

上述迭代公式在计算过程中一个核心的计算部分是Hessian矩阵的计算, 为了使计算更为稳定高效, 出现了多种修改Hessian矩阵的牛顿方法^{[15, 16, 17]}, 这类方法统称为拟牛顿理论。而L-BFGS理论是拟牛顿理论的一种, 其基本思想是对牛顿法中的Hessian矩阵用一个近似Hessian矩阵取代, 从而降低迭代过程中的储存要求和加快收敛速度。

将Hessian矩阵取代后的牛顿法迭代公式为^{[9, 18]}:

$\begin{matrix} Δ_{k} w = \frac{δ_{k}}{B_{k + 1}} 。 (10) \end{matrix}$

其中:

$\begin{matrix} \begin{matrix} δ_{k} = g_{k + 1} - g_{k}, (11) \\ B_{k + 1} = B_{k} - \frac{B_{k} s_{k} {s^{T}}_{k} B_{k}}{{s^{T}}_{k} B_{k} s_{k}} + \frac{δ_{k} {δ^{T}}_{k}}{{δ^{T}}_{k} δ_{k}}, (12) \\ s_{k} = w_{k + 1} - w_{k}, (13) \\ g_{k} = \nabla_{k} f (w), (14) \\ g_{k + 1} = \nabla_{k + 1} f (w) 。 (15) \end{matrix} \end{matrix}$

可以看出, L-BFGS方法虽然在迭代过程中利用了Hessian矩阵信息, 但是没有直接计算二阶导数, 只需要计算一阶导数。

实现流程如下^{[9, 18]}:

1) 给定初始w₀, 初始迭代次数k=0, 计算g₀, 若‖ g₀‖ ≤ ε , 则终止计算, w₀即为计算结果;

2) 根据式(9)求得搜索方向Δ _kw;

3) 用线性搜索求取迭代步长δ ^w, 线性搜索求取步长需要满足Wolfe条件, 即

$\begin{matrix} \begin{matrix} f (w_{k} + δ^{w} Δ w_{k}) \leq f (w_{k}) + c_{1} δ^{w} {g^{T}}_{k} Δ w_{k}, \\ \nabla f (w_{k} + δ^{w} Δ w_{k})^{T} Δ w_{k} \geq c_{2} {g^{T}}_{k} Δ w_{k} 。 \end{matrix} (16) \end{matrix}$

上式中, c₁和c₂为常数, 且满足0< c₁< c₂< 1。

4) 令α _k=δ ^w,

$\begin{matrix} w_{k + 1} = w_{k} + α_{k} Δ_{k} w; (17) \end{matrix}$

5) 根据式(10)计算B_k+₁, 置k=k+1, 循环计算。

4 算法

上文中分别建立了求解虚慢度的目标函数、目标函数梯度公式, 及求解方法, 实质上这只是算法的一部分, 为了完成整个复走时的计算, 需要拟定一个算法整体实现步骤。

本文的整体计算步骤为:

1) 确定射线路径并计算初值。当介质均匀时, 利用解析法进行计算; 当介质复杂时, 利用常规的射线追踪计算初始走时的实部τ _R0和虚部τ _I0;

2) 计算∇τ _R0和∇τ _I0, 并代入目标函数梯度公式, 进而得到初始梯度∇_w f(w₀);

3) 将得到的梯度代入第四节中的L-BFGS算法实现流程迭代计算w;

4) 将更新后的慢度w代入到利用迎风差分法离散后的方程(5), 利用快速推进法^[8]对复走时的实部进行更新;

5) 回到步骤2), 继续迭代。

5 计算精度与效率分析

5.1 均匀介质模型

为了验证算法的有效性, 并分析算法的精度和效率, 首先选取了均匀介质模型进行计算, 并对解析法、高斯牛顿— 共轭梯度(GN-CG)快速推进法、L-BFGS快速推进法计算结果进行对比。其中解析法公式为^[19]:

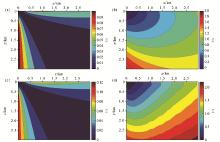
$\begin{matrix} \begin{matrix} τ_{R} = \frac{zcosθ + xsinθ}{v} + \\ \frac{(zcosθ + xsinθ) {(xcosθ - zsinθ)}^{2}}{2 v [{(zcosθ + xsinθ)}^{2} + b^{2}]}, \\ τ_{I} = b \frac{{(xcosθ - zsinθ)}^{2}}{2 v [{(zcosθ + xsinθ)}^{2} + b^{2}]} 。 (18) \end{matrix} \end{matrix}$

均匀介质模型大小为3 km× 3 km, 地下介质中地震波速度2 000 m/s。图1为出射角与z方向成45° 角走时虚部、实部对比图。射线起始点位置(1 500 m, 1 500 m), 波束半宽度1 000 m, 网格间距Δ x=10 m, Δ z=10 m。

	Figure Option View Download New Window
	图1 均匀介质中出射角与z方向成45° 角复走时分布对比 a— 解析法复走时虚部; b— 解析法复走时实部; c— L-BFGS快速推进法复走时虚部; d— L-BFGS快速推进法复走时实部; e— GN-CG快速推进法复走时虚部; f— GN-CG快速推进法复走时实部

表1给出了均匀介质中不同初始地震波(一类特殊的消散波)宽度和不同网格间距计算所耗CPU内存、耗时、平均相对误差定量对此情况。其中平均相对误差计算公式为:

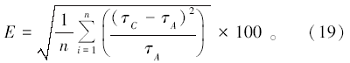
分析表1, 可以发现:①同等条件下, L-BFGS方法收敛速度快于GN-CG方法, 并且所耗内存较小、精度更高; ②因为实部的计算需要对迭代后的虚慢度和真实慢度离散, 因此计算的复走时虚部精度高于实部。

表1 均匀介质中L-BFGS方法和GN-CG方法计算精度和效率对比

5.2 常速度梯度模型

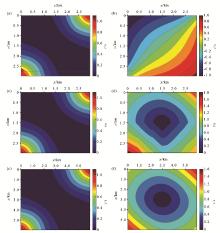
为了更为明显地对本文方法局部特征进行分析, 选取了在常速度梯度模型两个不同x位置, 不同z位置处的走时进行了对比。梯度介质模型大小为3 km× 3 km, 地震波速度v=v₀+0.5z, 其中v₀=1 500 m/s。网格间距Δ x=10 m, Δ z=10 m, 射线起始点位置(100 m, 100 m), 初始波宽为300 m, 图2为与竖直初始角度45° 弯射线复走时分布图, 梯度介质复走时计算解析公式为:

$\begin{matrix} \begin{matrix} τ_{R} = \frac{zcosθ + xsinθ}{(v_{0} + 0.5 z)} + \frac{(zcosθ + xsinθ) {(xcosθ - zsinθ)}^{2}}{2 (v_{0} + 0.5 z) [{(zcosθ + xsinθ)}^{2} + b^{2}]}, \\ τ_{I} = b \frac{{(xcosθ - zsinθ)}^{2}}{2 (v_{0} + 0.5 z) [{(zcosθ + xsinθ)}^{2} + b^{2}]} 。 \end{matrix} (20) \end{matrix}$

	Figure Option View Download New Window
	图2 梯度介质中复走时分布对比 a— 解析法复走时虚部; b— 解析法复走时实部; c— L-BFGS快速推进法复走时虚部; d— L-BFGS快速推进法复走时实部

5.3 周期性层状介质模型

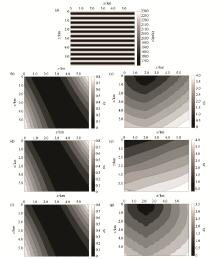
为了测试本文算法在更为复杂的模型中的适应性, 特别是分析在射线两侧介质不对称时本文复走时计算方法的效率和精度, 设计了周期性层状介质模型。该模型大小为6 km× 6 km, 介质中地震波速度:

$\begin{matrix} v = v_{0} [1 + 0.3 \cos (\frac{2 πz}{a_{0}})], (21) \end{matrix}$

其中, 平均速度v₀=2 000 m/s, 周期a₀=500 m。图3为与竖直初始角度成20° 弯射线, 射线起始点位置(2 000 m, 200 m), 网格间距Δ x=20 m, Δ z=20 m, 初始波宽500 m, L-BFGS快速推进法、动力学射线追踪法和GN-CG快速推进法复走时分布图。从图中的等值线可以看出, L-BFGS快速推进法和GN-CG快速推进法计算的复走时更能体现出速度的变化, 即速度周期层状性对每一条等值线的微小影响导致等值线不光滑, 其原因在于这两种方法用有限差分近似计算, 故能顾及邻近点速度变化。表2为两种方法所耗内存和计算时间对比。

表2 周期性介质模型中L-BFGS快速推进法和GN-CG快速推进法计算效率对比

	Figure Option View Download New Window
	图3 周期层状介质中复走时实部、虚部对比 a— 速度模型; b— L-BFGS快速推进法复走时虚部; c— L-BFGS快速推进法复走时实部; d— 动力学射线追踪法复走时虚部; e— 动力学射线追踪法复走时实部; f— GN-CG快速推进法复走时虚部; g— GN-CG快速推进法复走时实部

6 结论

本文通过引入L-BFGS方法改进了通过求解复程函方程计算复走时的方法。引入该方法主要是针对最优化求取虚慢度部分, 并对目标函数进行了修改, 从而对整体算法进行改进。分析表明, 本文的L-BFGS快速推进法无论是在计算速度上还是在准确性上都优于GN-CG快速推进方法, 因此本文改进后的算法更适用于实际应用时大规模计算复走时需求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Felsen L B. Evanescent waves[J]. Journal of the Optical Society of America, 1976, 66(8): 751-760. [本文引用:2]
[2]	Ĉervený V, Popov M MI. PšenČk I. Computation of wave fields in inhomogeneous media[J]. Geophysics, 1982, 70(1): 109-128. [本文引用:1]
[3]	Popov M M. A new method of computation of wave fields using Gaussian beams[J]. Wave Motion, 1982, 4(1): 85-97. [本文引用:1]
[4]	Hill N R. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428. [本文引用:1]
[5]	Hill N R. Prestack Gaussian beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. [本文引用:1]
[6]	Magnanini R, Talenti G. On complex-valued solutions to a 2D Eikonal equation. Part One: qualitative properties[J]. Contemporary Mathematics, 1999, 283: 203-229. [本文引用:1]
[7]	Li S, Fomel S, Vladimirsky A. Improving wave-equation fidelity of Gaussian beams by solving the complex eikonal equation[C]//San Antonio: Expand ed Abstracts of 81^stSEG Annual Internet Meeting, 2011: 3829-3834. [本文引用:4]
[8]	Sethian J A, Popovici A M. 3-D traveltime computation using the fast marching method[J]. Geophysics, 1999, 64(2): 516-523. [本文引用:2]
[9]	Huang X, Sun J, Sun Z. Local algorithm for computing complex travel time based on the complex eikonal equation[J]. Physical Review E, 2016, 93(4): 043307(1)-043307(10). [本文引用:3]
[10]	Perry A. A class of conjugate gradient algorithms with a two-step variable-metric memory[J]. Discussion Papers from Northwestern University, Center for Mathematical Studies in Economics and Management Science, 1977, 269. [本文引用:1]
[11]	Nocedal J. Updating quasi-Newton matrices with limited storage[J]. Mathematics of computation, 1980, 35(151): 773-782. [本文引用:1]
[12]	Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization[J]. Mathematical programming, 1989, 45: 503-528. [本文引用:1]
[13]	Bleistein N. Mathematical methods for wave phenomena[M]. Orland o: Academic Press, 1984. [本文引用:1]
[14]	Magnanini R, Talenti G. On complex-valued solutions to a two-dimensional eikonal equation. II. Existence theorems[J]. SIAM journal on mathematical analysis, 2003, 34(4): 805-835. [本文引用:1]
[15]	Schubert L K. Modification of a quasi-Newton method for nonlinear equations with a sparse Jacobian[J]. Mathematics of Computation, 1970, 24(109): 27-30. [本文引用:1]
[16]	Deuflhard P. A modified Newton method for the solution of ill-conditioned systems of nonlinear equations with application to multiple shooting[J]. Numerische Mathematik, 1974, 22(4): 289-315. [本文引用:1]
[17]	Dennis, Jr J E, Moré J J. Quasi-Newton methods, motivation and theory[J]. SIAM review, 1977, 19(1): 46-89. [本文引用:1]
[18]	Nocedal J, Wright S. Numerical optimization[M]. New York: Springer Science & Business Media, 2006. [本文引用:2]
[19]	Wu R S. Gaussian beams, complex rays, and the analytic extension of the Green’s function in smoothly inhomogeneous media[J]. Geophysical Journal International, 1985, 83(1): 93-110. [本文引用:1]

1976

0.0

... 为了处理这些现象,在上个世纪70年代,Feslen等人^[1]提出了将几何射线理论的相位部分,实质是对地震波走时,扩展为复值的一类波来模拟地震波传播,这类波被称为消散波(evanescent waves) ...

... 这其中包含了Felsen^[1]提出的等时面追踪法,基本思想是首先构建复走时实部、虚部的法线,然后分别根据射线方向和垂直与射线方向的网格增量来计算复走时 ...

1982

0.0

... 目前被广泛应用地震波模拟^[2,3]以及地震偏移^[4,5]的高斯波束就是这类消散波的一种 ...

1982

0.0

... 目前被广泛应用地震波模拟^[2,3]以及地震偏移^[4,5]的高斯波束就是这类消散波的一种 ...

1990

0.0

... 目前被广泛应用地震波模拟^[2,3]以及地震偏移^[4,5]的高斯波束就是这类消散波的一种 ...

2001

0.0

... 目前被广泛应用地震波模拟^[2,3]以及地震偏移^[4,5]的高斯波束就是这类消散波的一种 ...

1999

0.0

... Magnanini和Talenti^[6]提出的二阶非线性方程法,基本思想是利用数学变换对复走时的实部和虚部进行分离,分别建立实部和虚部所满足的非线性微分方程 ...

2011

0.0

... 为了克服上述方法的局限性,Li等人^[7]提出了基于复程函方程的扰动法 ...

... 由于方程(3)同时包含了复走时实部、虚部两个未知参数,给数值求解带来了困难,所以引入一个虚慢度w,将其分解为^[7]: ...

... 本文算法的目标函数与Li等^[7]的高斯牛顿#cod#x02014 ...

... 为此,引用Li等人^[7]通过扰动理论思想间接地建立目标函数的导数公式: ...

1999

0.0

... 为了求出这个慢度值,将复走时虚部、实部梯度正交的条件设为一个目标函数,然后再利用一个基于高斯牛顿法和共轭梯度法最优法(GN-CG)求出等效虚慢度,最后利用快速推进法^[8]计算复走时 ...

... 4) 将更新后的慢度w代入到利用迎风差分法离散后的方程(5),利用快速推进法^[8]对复走时的实部进行更新 ...

2016

0.0

... Huang等人^[9]在此基础上通过引入不等距有限差分处理波的非规则边界发展了局部复走时算法,由于该算法仅计算离波束中心射线较近部分的复走时,限制了计算范围,因此降低了计算量 ...

... 将Hessian矩阵取代后的牛顿法迭代公式为^[9,18]: ...

... 实现流程如下^[9,18]: ...

1977

0.0

... L-BFGS方法基本思想起源于Perry的研究^[10],Nocedal^[11],Liu和Nocedal^[12]对其进行了发展 ...

1980

0.0

... L-BFGS方法基本思想起源于Perry的研究^[10],Nocedal^[11],Liu和Nocedal^[12]对其进行了发展 ...

1989

0.0

... L-BFGS方法基本思想起源于Perry的研究^[10],Nocedal^[11],Liu和Nocedal^[12]对其进行了发展 ...

1984

0.0

... 1 复程函方程地震波实走时可以通过数值求解实程函方程^[13] ...

2003

0.0

... 将方程(2)代入式(1)中,并进行实部、虚部分离,得到^[14] ...

1970

0.0

... 上述迭代公式在计算过程中一个核心的计算部分是Hessian矩阵的计算,为了使计算更为稳定高效,出现了多种修改Hessian矩阵的牛顿方法^[15,16,17],这类方法统称为拟牛顿理论 ...

1974

0.0

1977

0.0

2006

0.0

... 将Hessian矩阵取代后的牛顿法迭代公式为^[9,18]: ...

... 实现流程如下^[9,18]: ...

1985

0.0

... 其中解析法公式为^[19]: ...