全波形反演大致分为3个关键步骤:目标函数的建立、梯度的求取、迭代反演。目标函数可直接影响全波形反演的非线性强度, 文中所用的目标函数是Tarantola在1984年提出的最小二乘目标函数。首先利用实际野外观测的地震记录与正演得到的模拟记录进行匹配, 求取波场的数据残差:

δd=uobs-ucal, (1)

然后用最小二乘的思想, 使误差函数

minm∈NE(v)=minm∈N‖δd‖22

最小。其中, m为模型空间N中的点。

梯度算子的构建是全波形反演中至关重要的一步, 其精度直接影响反演的速度。上世纪80年代Tarantola等人建立全波形反演理论框架的同时利用震源的正传波场与波场残差的反传波场进行互相关求取梯度算子, 避免了直接求取雅可比矩阵, 之后Plessix又重新推导了基于伴随状态法的时间域全波形梯度算子公式:

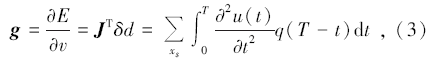
其中, v为传播速度, u(t)为震源的正传波场, J为波场u的雅可比矩阵, x_s为炮点的空间位置, T为正传波场的最大时间, q(T-t)为以波场数据残差δ d为震源进行波场逆时反传的波场记录。

从全波形反演的目标函数和求解过程, 可以看出, 正演模拟是全波形反演由初始速度模型得到模拟波场, 与实际波场进行对比并求取残差进而计算修正模型的关键步骤。要得到好的全波形反演效果必须保证正演模拟的稳定性、准确性。目前正演模拟算法常用的有射线法、有限差分法、有限单元法及有限差分法与Fourier法变换相结合的方法。这些方法各有优缺点。有限差分法在计算效率与计算精度上都比较好, 是较为常用的正演模拟方法。对常微分方程的任何一种计算格式, 都必须考虑它的稳定性和收敛性, 这是关系到算法成功与否的极其重要的问题。一个好的差分格式数值稳定性是差分格式的必要条件。因此, 在确定一个差分格式作为计算手段之前, 一定要研究差分格式的稳定性。

地球介质通常被假设为半无限空间介质, 而实际在进行计算机数值模拟时, 总是人为地限定了地球介质的计算区域, 这就引入了人为边界。这种人为边界上的反射通常比真正的物理界面的反射还要强, 将干扰有效波信息, 甚至可能掩盖一些有效波的信息, 必须加以消除或者尽量地减小这种边界反射。因此, 利用波动方程进行数值模拟, 一个关键问题就是边界条件。如针对一个二维模型进行叠前地震全波形反演, 如果正演模拟算法中边界条件选择不合适, 必定给反演结果带来较为严重的影响。

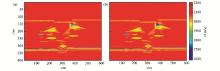
图1展示了不同边界条件下对应的正演记录, 从图中可以看出, 在边界条件不好的情况下, 有很明显的边界反射和虚假成像, 如图1a中红色方框标识的区域。

图1

	Figure Option ViewDownloadNew Window
	图1 不同边界条件对应的正演记录 a— 边界条件不好; b— 边界条件好

图2展示的是不同边界吸收情况对应的梯度结果。可以看出如果边界吸收情况不好, 对应的梯度会产生虚假地层的成像, 影响反演的结果。图2a所示的是没有将人工边界反射处理好, 图2b是吸收比较好的结果。

图2

	Figure Option ViewDownloadNew Window
	图2 不同边界条件对应的梯度 a— 边界条件不好; b— 边界条件好

目前大部分已发表文章都是针对理论模型的, 数据震源子波已知, 观测系统是规则的, 地震道能量均衡, 不含噪声特别是没有面波。但在实际资料应用中这些因素都是不可忽视的, 尤其是陆上资料观测系统严重不均匀, 缺炮现象广泛存在, 噪声多, 能量不均匀。这些因素直接影响反演结果的正确性与稳定性。叠前去噪、多次波压制、静校正等资料预处理问题及初始模型的建立是全波形反演资料预处理的关键。实际陆上地震资料面波能量强, 甚至其能量高于直达波振幅能量, 有效反射波被掩盖, 全波形反演中面波去除是不可或缺的一步环节。去除面波能量的同时还需要保留有效的地震波成分。

地震振幅的均衡处理也是常规地震处理流程中的重要环节, 由于采集观测系统设计问题, 检波器与地面耦合问题等都会造成不同检波点接收记录能量上的差异, 甚至能够达到几个数量级的差异, 必须进行能量均衡处理, 消除仪器等非地层因素引起的能量变化。

全波形反演可恢复速度场中的高波数成分, 速度场中低波数成分的构造需要在初始速度模型中给予准确的表达。因此初始速度模型的准确建立是全波形反演结果正确与否的关键问题之一, 可通过旅行时层析、速度分析等方法来构造初始速度模型。

图3给出了真实速度及两种不同的初始模型, 图3b中低波数成分的构造相对图3c中能更有效地表达。图4a、4b分别为由图3b、3c所示的初始模型反演得到的结果。图4a反射层可以正确归位, 图4b的深部反射层归位有误差, 证明速度中的低波数成分影响波传播的旅行时导致观测记录与模拟记录匹配时存在误差, 因此图4b的反演速度不能准确归位, 这种匹配误差较大时, 观测记录与模拟记录波形相差大于半个周期就会导致误差函数陷入局部极小而产生错误的反演结果。

图3

	Figure Option ViewDownloadNew Window
	图3 真实速度及不同的初始速度 a— 真实速度模型; b— 初始速度模型一; c— 初始速度模型二

图4

	Figure Option ViewDownloadNew Window
	图4 不同初始模型对应的反演结果 a— 图3b所示初始模型反演结果; b— 图3c所示初始模型反演结果

与覆盖次数和偏移距影响地震资料成像一样, 地震资料的覆盖次数和偏移距对全波形反演影响比较大。图5为不同偏移距对应的正演记录, 图6为不同偏移距对应的梯度, 图7为不同偏移距对模型反演速度结果, 对比分析可以看出偏移距越大上层低速体速度反演越好(在图中蓝色低速体的速度颜色越深), 从而导致下面平层反演的速度越直。

图5

	Figure Option ViewDownloadNew Window
	图5 不同偏移距的正演记录 a— 偏移距为1000 m; b— 偏移距为1500 m; c— 偏移距为3000 m

图6

	Figure Option ViewDownloadNew Window
	图6 不同偏移距对应的梯度 a— 偏移距为1000 m; b— 偏移距为1500 m; c— 偏移距为3000 m

图7

	Figure Option ViewDownloadNew Window
	图7 不同偏移距反演效果 a— 偏移距为1500 m; c— 偏移距为3000 m

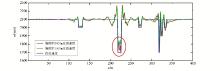
1 500 m 偏移距反演速度更加接近于真实速度。若偏移距较小, 由于低速体的存在可导致速度反演结果不准确, 发现当偏移距达到目的层1.5倍的时候反演效果要明显好于偏移距小的。尤其是低速体及低速体下方地层速度的构造形态和速度特征。图8为抽取不同偏移距对应的单道反演结果, 可以看出大偏移距对应的反演结果更接近真实值。所以, 增大偏移距可使信息更加丰富, 旅行时信息更准确, 上层速度反演效果更好, 因此下层速度轴可以拉直。

图8

	Figure Option ViewDownloadNew Window
	图8 单道反演结果

图9为不同覆盖次数得到的反演效果对比, 其中图9a为6个单炮得到的梯度, 图9b为44个单炮得到的梯度。可以看出:图9a因炮数少, 覆盖次数低, 有很明显的划弧现象; 而图9b覆盖次数提高, 划弧现象可以有效压制, 地下构造能清晰表达。

图9

	Figure Option ViewDownloadNew Window
	图9 不同覆盖次数反演效果对比 a— 6炮记录得到的梯度反演结果; b— 44炮记录得到的梯度反演结果

子波相位不同会使地震正演记录的波形不同, 子波相位越延迟, 正演波形越滞后, 从而导致反演结果也不相同, 如图10为选取的不同相位的子波, 图11为使用不同子波对应的反演结果, 可以看出, 当子波相位选取不准确, 会对反演的构造位置出现偏差, 相位越滞后, 反演构造位置越偏上。因此, 在实际应用中, 要根据地震数据准确地选取子波。

图10

	Figure Option ViewDownloadNew Window
	图10 不同相位的子波

图11

	Figure Option ViewDownloadNew Window
	图11 不同子波对应的反演结果