基于断层模型扫描的地质体边界识别方法与应用

引用本文

赵洋洋, 陈超, 石浩. 基于断层模型扫描的地质体边界识别方法与应用[J]. 物探与化探, 2016,40(5): 1035-1039.
ZHAO Yang-Yang, CHEN Chao, SHI Hao. The method of geological body boundary identification based on fault model scanning and its application[J]. Geophysical and Geochemical Exploration, 2016,40(5): 1035-1039.
Doi:10.11720/wtyht.2016.5.31 复制到剪切板

Permissions

基于断层模型扫描的地质体边界识别方法与应用

赵洋洋^1,², 陈超³, 石浩⁴

1.长安大学地质工程与测绘学院,陕西西安 710054

2.长安大学地质调查研究院,陕西西安 710054

3.中国地质大学(武汉) 地球内部多尺度成像湖北省重点实验室,湖北武汉 430074

4.中煤科工集团西安研究院有限公司,陕西西安 710077

作者简介: 赵洋洋(1987-),女,工程师,主要从事区域地质调查研究。E-mail:zhaoyang2013@chd.edu.cn

收稿日期: 2015-08-05

基金: 中国地质调查局“西准噶尔克拉玛依后山地区三维地质调查试点”项目(1212011220245)

摘要

如何较为准确地确定断层的位置及其产状一直是重力剖面数据解释的重点内容之一。笔者通过构建一系列具有不同几何参数(断层位置与倾角等)的2D断层模型,将其重力响应与观测重力剖面数据进行窗口滑动相关性扫描,根据计算的相关性系数最大值与设置的阈值比较,从而判断在滑动窗口中心点位置下方是否存在断层,若存在,则将相关性系数最大值对应的几何参数作为解释的断层参数。模型试验表明,利用该方法可以识别具有不同倾角的断层。利用该方法对某地区的实际重力剖面数据进行了多角度断层模型的相关性扫描,结果显示根据该方法确定的断层位置及倾角大小与实际断层地质剖面图比较一致,从而验证了笔者所提方法的有效性。

关键词: 重力剖面; 2D断层模型; 定量解释; 重力响应; 相关性扫描

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)05-1035-05 doi: 10.11720/wtyht.2016.5.31

The method of geological body boundary identification based on fault model scanning and its application

ZHAO Yang-Yang^1,², CHEN Chao³, SHI Hao⁴

1.Geology Engineering and Geomatics,Chang'an University,Xi'an 710054,China

2.Institute of Geological Survey,Chang'an University,Xi'an 710054,China

3.Hubei Subsurface Multi-scale Imaging Key Laboratory,China University of Geosciences,Wuhan 430074,China

4.Xi'an Research Institute of China Coal Technology & Engineering Group,Xi'an 710077,China

Abstract

Determining the locations and the dipping angles of the faults is one of the most important issues in the interpretation of the gravity profile data.The authors first construct a series of 2D fault models with different geometric parameters (e.g., locations and dipping angles).Then the theoretical gravity responses of the models are applied to the correlation scanning with the observing gravity profile data in the moving windows.According to the comparison between the calculated correlation values and the threshold value,we can judge whether the faults exist or not beneath the centers of the windows.If the faults exist,the corresponding geometric parameters of the maximum correlation value are treated as the interpretation results.The synthetic model tests suggest that it is effective to identify the faults with different dipping angles.Moreover,the correlation scanning method is applied to an actual profile of the gravity data in field,and the results show that the determined locations and dipping angles of the faults by the proposed method are consistent well with those of the known faults detected by surface geological survey and other geophysical probes.Therefore,both the synthetic tests and the field example indicate the validity of the method presented in this paper.

Keyword: gravity profile; 2D fault model; quantitative interpretation; gravity response; correlation scanning

Show Figures

在断层等地质体的边界区域, 往往存在横向密度变化, 因此利用重力数据可以寻找与识别断裂, 如何准确地判断与提取断层的位置以及确定断层的倾向与倾角, 对于利用重力数据进行地质构造解释具有重要意义。但是, 以往的研究侧重于平面重力异常数据线性信号的增强与提取, 进而识别与划分断裂系统^{[1, 2, 3, 4, 5]}。相对而言, 比较缺乏针对重力剖面数据的断层几何参数定量解释方法。在一般情况下, 利用垂直于断裂走向的重力剖面精测数据, 可以将断裂构造简化为二度体的倾斜台阶组合模型^[6]。Stanley和Green^[7]提出在理想情况下, 以二度台阶重力异常的垂向梯度g_z为横坐标x、水平梯度g_x为纵坐标y作图, 可以得到一个椭圆, 并且证实了该近似椭圆型的梯度空间图的长轴方向与横坐标轴的夹角即对应着倾斜台阶模型的斜面倾角。魏伟和刘天佑^[8]利用一个二次曲线方程拟合该椭圆参数, 从而实现地下台阶(或断层)倾角的自动与快速计算。王同庆等^[9]通过理论模型试验发现, 利用基于二次曲线方程最小二乘拟合方法计算的台阶倾角受模型的埋深或厚度影响严重, 甚至会得到错误的倾角, 因此提出利用基于椭圆标准方程的非线性回归方法进行椭圆拟合, 其模型试验与实际应用均表明改进后方法的稳定性与准确性均得到提升。在此论文中, 笔者在认真研读相关系数扫描方法^{[10, 11, 12, 13, 14, 15]}在重磁平面数据中运用的文献资料后, 尝试对重磁剖面数据的处理提出一种新的解决方案, 即利用2D断层模型的理论重力响应与重力剖面数据进行窗口滑动相关性扫描, 以判断是否存在断层以及确定断层的几何参数, 旨在为重力剖面数据的断层定量解释提供辅助方法。

1 基于2D断层模型理论重力响应的滑动相关性扫描

1.1 方法原理

该方法的原理为:首先, 构建系列具有不同位置与倾角等参数的2D断层模型; 然后, 在滑动窗口内计算断层模型的理论重力响应(也可称之为断层子波)与实测数据的相关性; 最后, 根据相关性阈值判断在滑动窗口正下方是否存在断层, 若存在则选取相关性最大值对应的断层模型参数作为解释结果。

重力剖面数据第i点的相关系数计算公式:

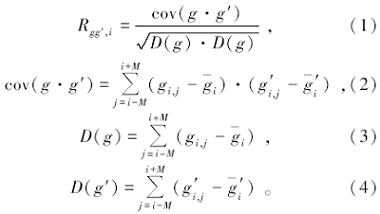
其中:cov(g· g')、D(g)与D(g')分别表示滑动窗口内断层模型重力响应g_i_,_j与观测数据 $\begin{matrix} g_{i, j}^{'} \end{matrix}$ 之间的协方差及各自的方差; j为滑动窗口内的移动点, (M× 2+1)为滑动窗口内理论响应或观测点的个数; $\begin{matrix} {\overset{̅}{g}}_{i} \end{matrix}$ 与 $\begin{matrix} {\overset{̅}{g}}^{'}_{i} \end{matrix}$ 分别为滑动窗口内断层模型重力响应与观测数据的平均值。

相关系数R_gg'即表示选取窗口内实际重力异常与模型重力响应之间的相关程度。显然地, 如果将g与g'换成重力水平导数则会提高断层的水平分辨率, 并且降低断层之间的相互干扰, 此时应该选取较小的窗口。

1.2 断层子波

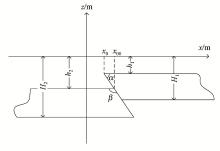
断层模型作为扫描对比的基础, 其理论重力响应主要由断层模型倾角(α )、断层厚度(H₁-h₁与H₂-h₂)、两盘埋深(h₁或h₂)与水平位置(x₀与x₀₀)、断层水平延伸长度(L₁与L₂)、断层与围岩的密度差异(Δ ρ )及观测高度(Z₀)因素决定(图1)。由于本文假设断层模型两盘水平无限延伸且两盘厚度相等, 并且相关性扫描只考虑重力响应形态而不考虑幅值, 因此笔者仅以倾角、断层厚度与深度作为单变量进行模型重力异常值及重力异常水平导数值的计算比对, 以期寻找对断层子波形态变化最敏感的因素。

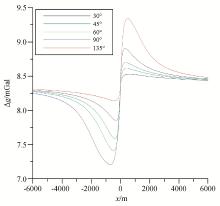
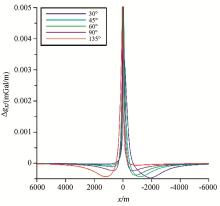
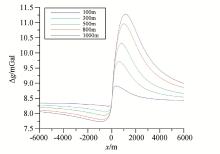
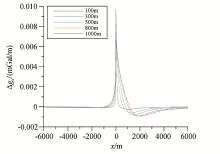
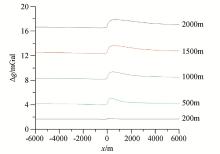
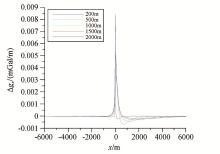
	Figure Option View Download New Window
	图1 断层模型的几何示意

通过数值计算得到了单一因素下的断层子波(图2~图7), 通过对子波形态的分析认为:当角度作为变量时, 各子波形态差异较大; 当两盘埋深作为变量时, 各子波形态的差异也较大, 但是在实际数据处理中, 经异常分离之后的局部异常所反映的断裂往往切割整个目标深度(如5 km以浅), 因此其对异常形态的影响不予考虑; 当模型厚度作为变量时, 其对子波形态的影响最小。由于文中只考虑了重力异常的形态而非幅值, 因此笔者所提方法主要在于估计断层的水平位置与倾向、倾角。

	Figure Option View Download New Window
	图2 不同倾角断层模型重力异常响应

	Figure Option View Download New Window
	图3 不同倾角断层模型重力异常水平导数响应

	Figure Option View Download New Window
	图4 不同左盘埋深断层模型重力异常响应

	Figure Option View Download New Window
	图5 不同左盘埋深断层模型重力异常水平导数响应

	Figure Option View Download New Window
	图6 不同厚度断层模型重力异常响应

	Figure Option View Download New Window
	图7 不同厚度断层模型重力异常水平导数响应

2 模型试验

为了试验文中所提方法对断层水平位置及断层倾向、倾角的识别效果, 首先设计了不同角度的断层模型进行试验。值得注意的是, 为了获取不同角度断层模型的完整重力响应值, 笔者选取6 000 m的范围根据断层倾角变化调节取值范围; 异常值的取值间隔为20 m, 剩余密度取0.2 g/cm³。系列模型的具体参数见表1, 断层模型如图1所示。

表1 不同倾角的2D断层模型参数

模型试验结果表明(表2与表3):各个扫描角度除了自相关结果为1之外, 随着角度与理论值差距的变大相关系数值逐渐减小甚至为负值; 由同一模型重力异常水平导数的相关系数结果可以看出, 经过导数变换之后的扫描结果对角度变化更加敏感, 对于同样的两个模型角度, 其相关系数值更小。因此, 根据上述模型试验结果, 证明了利用窗口相关系数扫描的方法可以识别不同角度的断层。

表2 基于重力扫描的相关系数值

表3 基于重力水平导数扫描的相关系数值

当然, 扫描窗口的大小对相关系数的大小也具有影响。笔者在设置模型取值范围时已力求保证子波形态完整的情况下窗口尽量小的原则, 因此本文在不同的模型试验中, 模型的取值范围存在差异。在实际数据扫描时, 本文设计以起始点开始逐点移动扫描求取相关系数并且保留中心点处的最大相关值为原则的循环扫描方法对数据进行处理, 以期最大程度地规避各种不确定性因素对断层位置判断的影响。

3 实际应用

为了验证文中所提方法的实际应用效果, 此处以新疆西准噶尔后山地区的某测线实测数据断层解释作为应用实例。在实际数据处理时, 为了简化计算过程同时保证重力异常的完整性, 设计模型取值范围为(-3 000+3× tanα × h, +3 000+3× tanα × h), 取值间隔与实际数据采样间隔保持一致为20 m, 模型顶底埋深对异常形态影响较小因而分别设置为:h₁=200 m、h₂=1 200 m。笔者设计了以5° 为间隔的、从30° ~150° 变化的多角度断层子波模型与实际剖面逐点循环进行相关系数扫描, 以相关系数值为依据得到断裂或地层位置及对应的角度值, 从而实现利用重力剖面数据识别与提取断层信息。

取该剖面上的10 km范围进行断层扫描, 结果如图8所示。结合实际资料分析认为, 重力异常扫描结果(红色+)取相关系数值为0.6以上的认为其相关性较好, 可能存在断层; 重力水平导数扫描结果(蓝色+)取相关系数值为0.5以上的认为其相关性较好, 即可能存在断层。根据两者综合推断的断层位置、倾向与倾角以蓝色短虚线(F₁~F₅)示于地质剖面图之上, 可以看出对于该区地表出露的断裂, 无论是倾向还是倾角基本与笔者推断结果一致, 位置约有0.5 km的偏差。

	Figure Option View Download New Window
	图8 某实测重力测线的2D断层子波扫描结果

4 结论

笔者提出基于2D断层模型理论重力响应(或子波)相关性扫描的重力剖面数据定量解释方法, 通过模型试验与实际应用, 验证了文中所提断层识别与定量解释方法的有效性。其中, 重力水平导数的相关系数值反映出其对断层角度的识别更加敏锐, 相较而言重力本身的扫描结果会丢失一些角度较小的断层信息。因此, 在实际应用之中, 考虑不同角度模型时以重力水平导数的扫描结果为主, 结合相关性较高的重力扫描结果, 综合判断断层水平位置及其倾向、倾角, 推断结果与该区的地质剖面结果吻合较好, 为该区地质解释给出地球物理依据。值得说明的是, 相关性扫描方法对噪声并不敏感, 但是若在处理之前进行适当的去噪处理, 可以改善扫描结果。当然, 由于文中只考虑了形态相关性而未考虑幅值的接近程度, 因而该方法在断层厚度与深度以及密度差异上的研究还有待于进一步地完善。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展[J]. 地球物理学进展, 2010, 25(1): 196-210. [本文引用:1]
[2]	Cooper G R J, Cowan D R. Enhancing potential field data using filters based on the local phase[J]. Computer &Geosciences, 2006, 32: 1585-1591. [本文引用:1]
[3]	Cooper G R J, Cowan D R. Enhancing linear features in image data using horizontal orthogonal gradient ratios[J]. Computers & Geosciences, 2007, 33: 981-984. [本文引用:1]
[4]	Cooper G R J, Cowan D R. Edge enhancement of potential-field data using normalized statistics[J]. Geophysics, 2008, 73(3): H1-H4. [本文引用:1]
[5]	余钦范, 楼海. 水平梯度法提取重磁源边界位置[J]. 物探化探计算技术, 1994, 16(4): 363-367. [本文引用:1]
[6]	曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2006. [本文引用:1]
[7]	Stanley M, Green R. Gravity gradients and interpretation of the truncated plate[J]. Geophysics, 1976, 41(6): 1370-1376. [本文引用:1]
[8]	魏伟, 刘天佑. 梯度法解释复杂二维断裂重力异常[J]. 物探与化探, 2005, 29(4): 347-350. [本文引用:1]
[9]	王同庆, 陈超, 董运洪, 等. 改进的重力异常梯度法在二维断层几何参数定量解释中的应用[J]. 大地测量与地球动力学, 2013, 33(6): 81-85. [本文引用:1]
[10]	王宜昌. 褶积在重力资料解释中的应用[J]. 石油地球物理勘探, 1983, 18(5): 457-463. [本文引用:1]
[11]	王慎中. 滤波因子Vzz在重力资料褶积处理中的应用[J]. 江汉石油学院学报, 1991, 13(3): 30-36. [本文引用:1]
[12]	王正科, 田舍, 李久亮, 等. 滑动相关分析在重磁资料解释中的应用[J]. 物探与化探, 2005, 29(5): 409-413. [本文引用:1]
[13]	谈小生. 相关系数及其在矿产资源预测中的应用[J]. 长春地质学院学报, 1994, 21(4): 469-474. [本文引用:1]
[14]	马国庆, 杜晓娟, 李丽丽. 利用水平与垂直导数的相关系数进行位场数据的边界识别[J]. 吉林大学学报: 地球科学版, 2011, 41(1): 345-348. [本文引用:1]
[15]	刘燕戌, 李文勇, 徐建春. 航空重、磁异常相关性分析方法及其应用[J]. 物探与化探, 2012, 36(5): 783-787. [本文引用:1]

2010

0.0

王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展[J]. 地球物理学进展, 2010, 25(1): 196-210.

The study on the edge location of the geological body is the eternal topic of the potential data interpretation, and this is also its advantage. In recent years, the articles about edge recognition using potential data are increasing apparently both at home and abroad. However, no author systematically arranged and compared advantages and disadvantages of each method. This brings much inconvenience to users. First of all, the methods of edge recognition are classified into three kinds of methods. They are Mathematical Statistics, Numerical Calculation and Other Methods, meanwhile the current situation of these methods have been outlined. Additionally, we summarized the fundamental methods of edge detection which are the vertical derivative(VDR), total horizontal derivative(THDR), analytical signal amplitude(ASM), tilt angle(TA) and θ map(Theta Map).We also described the researching history and the applied effect of TA_THDR(Total Horizontal Derivative of the Tilt Angle) which have been developed based on the fundamental methods of edge recognition. Based on this, we have contrasted the effects of the main methods of edge recognition through the synthetic model. Through summary, contrast and analysis, we have presented some problems that should be paid attention in edge recognition and have suggested the future research emphasis and developing direction.

研究地质体的边缘位置是重、磁位场数据解释永恒的主题，也是其优势.最近几年，国内外利用重、磁位场进行地质体边缘识别研究的文章明显增多，但没有作者系统整理和对比各方法的优点和缺点，给使用者带来诸多不便.本文首先将现有重、磁位场边缘识别方法分为数理统计、数值计算和其他三大类，并概述了各类方法的研究现状；之后较详细总结了数值计算类中垂向导数、总水平导数、解析信号振幅、倾斜角、 θ 图这5种基本的边缘识别方法以及在这些基本方法之上发展起来的诸如倾斜角总水平导数、增强解析信号振幅等方法的研究历史和应用效果；并用理论模型对比了几种主要边缘识别方法的识别效果.通过以上总结、对比和分析，指出了重、磁位场边缘识别方法使用中需要注意的问题以及将来的研究重点及发展方向.