迭代是数学上的一种求解方程的方法, 也叫逐次逼近法, 是一种通过求近似根的序列收敛, 最终得到较为精确解的过程^[10]。迭代过程是不断重复的, 每一次对过程的重复即称为“ 迭代” , 每次迭代是为了逼近所设目标, 且每一次迭代的初值不同^{[11, 12]}。迭代过程的复杂性, 使得人们更加依赖于运算速度快、适合做重复性操作的计算机去实现。迭代过程需要确定变量和迭代结束的条件。

化探数据处理过程中, 为了使不服从正态分布的元素数据集合呈现正态或接近于正态分布, 采用了迭代剔除(替换)。在此过程中, 迭代变量为元素(值), 迭代规则为:剔除> x̅i+kS_i和< x̅i-kS_i(k可取2、2.5、3)的离群值, 迭代结束条件是:没有离群值的存在, 使得元素的概率分布接近于正态形式。计算机实现过程如下^{[13, 14, 15]}:

1) 计算初始数据集中某元素的算数平均值( x̅1)和标准离差(S₁);

2) 将> x̅1+kS₁和< x̅1-kS₁值进行剔除, 获得一个新数据集, 再计算此数据集的均值( x̅2)和标准离差(S₂);

3) 检查有无> x̅2+kS₂和< x̅2-kS₂的值存在, 若有, 则进行重复剔除(迭代)。以此类推, 重复过程2), 直至无离群值的存在。

4) 求出最终数据集的均值( x̅n)和标准离差(S_n), 将均值( x̅n)作为背景值, x̅n+jS_n(j可取1.5、2或3)作为异常下限^[16]。

剔除方式可以换作替代, 即将离群值用 x̅i+kS_i来迭代替换后进行统计。

由上可见, 化探数据的迭代过程是一个有限次的线性迭代。

在进行中国地质调查局地质矿产调查专项“ 中大比例尺化探数据一体化处理系统研究” 项目研究时, 为了实现化探数据迭代过程的自动化, 开发了“ 特异值检查” 模块, 用来进行数据的迭代处理、背景值及异常下限的统计。利用此功能, 可以实现迭代过程的自动化处理和结果的可视化显示, 主要功能界面如图1所示。

图1

	Figure Option ViewDownloadNew Window
	图1 自动化迭代过程功能界面

界面主要分为7个功能区:

①区为迭代条件的设置, k值默认为3, 用户可以自定义。

②区为异常上下限的计算公式。

③区为数据类型的选择, 默认为对原始数据迭代, 可选择数据取对数后再迭代。

④区为迭代变量的选择, 变量为单个或多个元素。

⑤区为迭代结果的可视化显示, 可以查看迭代过程中每次剔除点的情况(图2)。图2表明Cu经过了4次迭代处理。图中不同的颜色显示了每次处理时所剔除的点个数及其位置。

图2

	Figure Option ViewDownloadNew Window
	图2 迭代剔除过程的可视化显示

⑥正态分布曲线, 浏览查看每次剔除后元素的正态分布曲线(图3)。图3表明经过4次迭代处理的Cu每次迭代后所具有的概率分布形式及其平均值的大小、背景区间。

图3

	Figure Option ViewDownloadNew Window
	图3 Cu迭代剔除过程中的正态分布曲线

⑦计算获得结果, 获得的统计结果如表1所示。结果记录了每一次剔除时的各项参数。

表1

表1

表1 Cu迭代剔除结果 迭代 次数 样点 个数 替换 点数 算术 几何平 均值 标准 离差 变异 系数 异常 下限 富集 系数 偏度 峰度 最小值 最大值 平均值 中位数 0 7114 0 0.9 1358 18.4 16.5 15.5 19.4 1.05 57.1 1.08 47.2 3230.5 1 7087 27 0.9 76 17.8 16.4 15.4 9.5 0.53 36.8 1.05 1.2 5.9 2 6991 96 0.9 46.1 17.3 16.3 15.2 8.4 0.48 34.1 1.02 0.5 2.7 3 6954 37 0.9 42.3 17.2 16.2 15.1 8.2 0.48 33.5 1.01 0.4 2.4 4 6949 5 0.9 41.7 17.2 16.2 15.1 8.2 0.48 33.5 1.01 0.4 2.4 5 6947 2 0.9 41.6 17.2 16.2 15.1 8.1 0.47 33.4 1.01 0.4 2.4 6 6945 2 0.9 41.4 17.1 16.2 15.1 8.1 0.47 33.4 1.01 0.4 2.4 注:含量单位为10-6

表1 Cu迭代剔除结果

化探数据的迭代过程, 由于参数众多(如k取值不同)、方式不同(剔除和替代)、数据形式不同(原始数据和取对数)、迭代规则不同( x̅1± kS₁或 x̅1+kS₁)、计算过程复杂, 所以迭代在化探工作者的心中一直是一个未解的过程。笔者利用特异值剔除模块分别对k取值和取对数迭代对分析结果的影响进行了剖析。此处利用的数据为河北某地1:50 000的普查数据, 个数为7 114个。

3.1 取不同k值的结果比较

将k取不同的值时, 获得的结果如表2。从表2可以看出, 当k为3、 2.5、 2时, 迭代剔除的次数和点数随k值的减小呈明显的增加, 从而导致算数平均值和异常下限值的减小。但是k为3、2.5时, 差别不明显; k为3、2时差别显著。

表2

表2

表2 k取不同值时的迭代结果比较 元素 k=3 k=2.5 k=2 剔除 次数 剔除的 点数 算数平 均值 标准 离差 异常 下限 剔除 次数 剔除的 点数 算数平 均值 标准 离差 异常 下限 剔除 次数 剔除的 点数 算数平 均值 标准 离差 异常 下限 Ti 4 39 1923 1246 4414 3 90 1899 1219 4336 32 3342 954 375 1704 V 3 52 52.7 29.7 112 3 115 52 28.9 109.7 4 329 50.1 27.2 104.5 Cr 3 110 45.3 27.1 99.4 4 191 44.5 26 96.6 10 489 42.1 24 90.1 Mn 7 420 739 316 1371 9 649 711 283 1277 15 1546 701 216 1133 Co 3 65 9.8 5 19.7 3 119 9.6 4.9 19.4 5 334 9.3 4.6 18.5 Ni 6 141 21.7 11.9 45.6 7 308 20.9 11.1 43 13 967 18.7 9.1 36.8 Cu 6 169 17.1 8.1 33.4 6 268 16.8 7.8 32.4 9 577 16.1 7.1 30.4 Zn 3 109 51.3 23.3 97.8 3 139 51 22.9 96.9 7 342 49.6 21.7 93 Mo 5 371 0.69 0.26 1.22 8 610 0.67 0.23 1.14 8 1227 0.63 0.19 1.02 Ag 3 159 0.05 0.011 0.072 3 258 0.05 0.01 0.071 6 1021 0.05 0.008 0.066 Cd 6 534 0.128 0.048 0.224 8 981 0.119 0.038 0.196 8 1762 0.114 0.029 0.171 As 24 844 5.4 3.2 11.8 20 1631 4.4 2 8.5 26 2940 3.6 1.2 6 Au 8 426 0.7 0.3 1.3 9 715 0.7 0.3 1.2 16 2024 0.6 0.2 0.9 Hg 6 159 10 3 15 7 987 9 2 13 6 1518 9 2 12 注: Au、Ag含量单位为10-9, 其他元素为10-6。表3同

表2 k取不同值时的迭代结果比较

化探数据在迭代处理时, k值究竟应该选择哪个数值最为恰当, 作者认为应该从迭代处理的目的去考虑。迭代处理的目的是在剔除高值点的同时使元素呈现正态分布, 从而获得适宜的背景值。按照正态分布的3α 法则:μ 为平均值, σ 为标准离差, 在[最小值, μ -3σ ]和[μ +3σ , 最大值]范围中仅占有0.3%的数据量, 此范围称为极端异常区, 此区内的数据称为离群值, 所以k=3为首要的选择。在表2中, 若选择k=3时, 最大剔除量为844个数据点; 当k=2时, 最大剔除点数达到3 342个, 几乎近一半为离群点, 显然不切合实际。

3.2 原始数据迭代和取对数迭代的结果对比

利用实测数据进行原始数据迭代和取对数迭代, 迭代剔除的规则为剔除> x̅i+3S_i和< x̅i-3S_i的离群值, 异常下限= x̅i+2S_i, 统计结果如表3, 其中, 取对数统计的结果又分为按对数进行统计和按对应的真值进行统计两部分。

表3

表3

表3 1:50 000数据真值迭代剔除和取对数迭代剔除结果对比 元素 原始数据剔除 取对数剔除 迭代 次数 剔除的 点数 按对数值统计 按对应真值的统计 迭代 次数 剔除的 点数 算数 平均值 标准 离差 异常 下限 算数 平均值* 标准 离差* 异常 下限 几何 平均值 标准 离差 异常 下限 Ti 4 39 1923 1246 4414 2 28 3.187 0.315 6561 1539 1287 4113 V 3 52 52.7 29.7 112 4 101 1.647 0.303 178.6 44.3 30.9 106.2 Cr 4 110 45.3 27.1 99.4 1 16 1.567 0.326 165.6 39.6 31 99 Mn 8 420 739 316 1371 5 136 2.856 0.228 2051 718 460 1637 Co 3 65 9.8 5 19.7 1 13 0.924 0.269 28.9 8.4 5.4 19.2 Ni 6 143 21.7 11.9 45.6 3 39 1.271 0.278 67.3 18.7 13.7 46.1 Cu 6 169 17.1 8.1 33.4 3 61 1.193 0.237 46.6 15.6 9.6 34.7 Zn 3 109 51.3 23.3 97.8 3 45 1.666 0.231 133.9 46.3 29 98.4 Mo 5 371 0.69 0.26 1.22 7 132 -0.717 0.187 1.60 0.67 0.34 1.36 Ag 3 159 0.05 0.011 0.072 4 129 -1.304 0.098 0.078 0.05 0.011 0.072 Cd 6 534 0.128 0.048 0.224 3 110 -0.893 0.193 0.311 0.128 0.072 0.272 Sn 8 456 1.9 0.6 3.1 7 218 0.283 0.158 4.0 1.9 0.8 3.5 Sb 7 374 0.35 0.17 0.7 3 26 -0.483 0.244 1.01 0.33 0.24 0.81 W 8 408 1.04 0.49 2.01 4 117 -0.004 0.249 3.12 0.99 0.72 2.43 Pb 4 115 20.1 6.3 32.8 4 172 1.292 0.139 37.1 19.6 6.4 32.5 Bi 6 373 0.24 0.09 0.42 5 212 -0.619 0.173 0.53 0.24 0.11 0.46 As 24 844 5.4 3.2 11.8 2 31 0.734 0.322 23.9 5.4 6.4 18.2 Hg 6 609 10 3 15 4 267 0.981 0.13 17.4 10 3 16 Au 8 426 0.7 0.3 1.3 6 141 -0.172 0.198 1.7 0.7 0.4 1.4 注:“ * ” 表明数据为对数值; 表中数据在自动统计时, 是按双精度的字段分别进行统计, 然后按表达精度进行小数位取舍

表3 1:50 000数据真值迭代剔除和取对数迭代剔除结果对比

从表3可以看出, 原始数据迭代过程的次数和剔除点数要远远多于以对数方式进行的迭代次数和点数, 只有1个元素稍有不同。

同时, 利用对数算数平均值和对数标准离差计算异常下限转换后的真值 , 均远远高于原始数据的迭代结果。这是长期以来一直困扰着化探工作者的问题。在实际科研生产中, 为了获得较低的异常下限, 往往将对数计算时标准离差的倍数从2降为 1.65, 这是一种没有依据的人为妥协。

经过研究发现, 利用取对数后的对数计算获得的异常下限过高, 这是由于对数标准离差的误用而引起的。

已知某元素i在n个采样点上的分析数据为

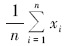
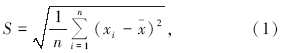
x₁、x₂、x₃、…、x_n, 则其原始数据的算数平均值为 , 标准离差为

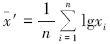
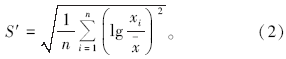
其对数的算术平均值为 , 标准离差为

从式(1)和式(2)可以看出, 对数算术平均值的真值即为原始数据的几何平均值。但是对数标准离差的真值并不对应实际真值的标准离差, 也就是说对数标准离差和原始数据取对数再剔除后的真值的标准离差是不相等的。所以利用对数的平均值和2倍标准离差求和后再取真值, 由于呈指数数量级的变换, 因此所获异常下限往往过大。实际应用中, 以对数方式计算, 有的元素异常下限值最大能超过按原始数据迭代所获异常下限的1/3, 这显然是标准离差的误用引起的。

从表3中还可以发现, 对数迭代过程中, 若按对应真值的几何平均值和此时真值的标准离差进行统计, 就不会出现异常下限过高的结果。尽管对数迭代过程次数少, 剔除的离群值数据点少, 其标准离差会大于原始数据迭代替换时的标准离差, 但是因为几何平均值永远小于算数平均值, 所以以此方式求得的异常下限有时甚至小于原始数据迭代的结果, 但总体上二者是一致的, 数据也是可用的。这可以说明, 用真值和取对数分别进行迭代处理, 求得的异常下限是吻合的。

“ 特异值检查” 模块在进行取对数迭代时, 最后提供了两个数据结果, 一个是按照对数进行统计的结果, 一个是按照对应真值进行统计的结果。按对应真值直接获得的标准离差才是正确的结果, 这也说明利用几何平均值和真值的标准离差计算获得的异常下限可以被利用。

化探数据处理中迭代剔除过程是一个数据进行重复计算的复杂过程。利用计算机技术及可视化技术开发获得的“ 特异值检查” 功能, 将化探数据的迭代处理过程实现了自动化和可视化, 从而可以解释模糊或无从证实的疑问, 获得明确的结论。这也说明, 充分利用先进的计算机技术, 化探数据处理过程可在实现数据处理自动化、可视化甚至智能化的同时, 对化探数据本身蕴含的规律有新的理解和认识, 这些认识必将进一步促进方法技术的发展和进步。