相关性分析在GT航空重力仪零漂改正中的应用

引用本文

屈进红, 郭素然, 周锡华, 姜作喜, 刘乾坤. 相关性分析在GT航空重力仪零漂改正中的应用[J]. 物探与化探, 2016,40(4): 838-842.
QU Jin-Hong, GUO Su-Ran, ZHOU Xi-Hua, JIANG Zuo-Xi, LIU Qian-Kun. The correlation analytical method and its application to GT aerogravimeter drift correction[J]. Geophysical and Geochemical Exploration, 2016,40(4): 838-842.
Doi:10.11720/wtyht.2016.4.32 复制到剪切板

Permissions

《物探与化探》编辑部所有

相关性分析在GT航空重力仪零漂改正中的应用

屈进红^1,², 郭素然³, 周锡华^1,², 姜作喜^1,², 刘乾坤¹

1.中国国土资源航空物探遥感中心,北京 100083

2.国土资源部航空地球物理与遥感地质重点实验室,北京 100083

3.国际关系学院心理教育研究中心,北京 100091

作者简介: 屈进红(1981-),男,江苏无锡人,工程师,2007年毕业于成都理工大学地球物理系固体地球物理学专业,现主要从事航空地球物理探测技术、数据处理、航空重力减振技术及相关技术的应用研究工作。

收稿日期: 2015-12-14

基金: 国家高技术研究发展计划(“863”计划)“新型高精度航空重力勘查系统研制”项目(2013AA063902); 中国地质调查局地质调查“航空重力测量技术规范”项目(12120115054801)

摘要

航空重力仪测量传感器和地面重力仪测量单元类似,往往存在零点漂移现象,通常把这种漂移视为线性关系,用前、后校数据做零漂改正处理。但是航空重力仪结构复杂,造成传感器漂移的因素很多,最为关键的因素是环境温度变化带来的扰动,实际又无法避开航空重力仪在温差剧烈变化的夏、冬两季作业。笔者以航空重力仪静态数据为例,首先进行固体潮改正并使用最小二乘法做线性零漂改正,其次使用线性相关分析方法,获得了静态数据和仪器温控温度之间具有很强的相关性特征,最后建立线性回归方程计算得到最终改正后的重力静态数据,精度有了很大的提高。这种相关性分析方法对深入理解传感器零漂改正处理方法和应用于动态测量数据中的零漂改正预研究具有实际意义。

关键词: 航空重力仪; 固体潮改正; 零漂改正; 最小二乘法; 相关性分析

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)04-0838-05 doi: 10.11720/wtyht.2016.4.32

The correlation analytical method and its application to GT aerogravimeter drift correction

QU Jin-Hong^1,², GUO Su-Ran³, ZHOU Xi-Hua^1,², JIANG Zuo-Xi^1,², LIU Qian-Kun¹

1.China Aero Geophysical Survey and Remote Sensing Center for Land and Resources,Beijing 100083,China

2.Key Laboratory of Airborne Geophysics and Remote Sensing Geology,Ministry of Land and Resources,Beijing 100083,China

3.Psychological and Educational Research Center,University of International Relations,Beijing 100091,China

Abstract

In airborne gravimeter and ground gravimeter measurement unit,there often occur drift phenomena.If this drift is regarded as a linear relationship,the first and last data are used to do drift correction process.Nevertheless,the airborne gravimeter structure is complex,and the sensor drift is caused by many factors,with the most critical factor being the environment temperature change disturbance.It is impossible for us to avoid airborne gravity dramatic changes in the temperature difference of flight measurement between summer and winter.The authors used the airborne gravimeter static data as an example.First,the data need gravity tide correction and drift correction by using a least squares method.Secondly,correlation analysis is used to analyze the static data and instrument thermostatic temperature to obtain a strong correlation characteristics.Finally,linear regression equation is set up to calculate the static data and,as a result,the gravity of the final corrected precision is greatly improved.This correlation analysis method has practical significance for the in-depth understanding of sensor drift correction methods and pre-study of dynamic measurement data in the drift correction.

Keyword: airborne gravimeter; gravity tide correction; drift correction; least squares method; correlation analysis

Show Figures

众所周知, 地面相对重力仪的核心测量单元弹性元件(弹簧)均存在零点漂移, 这是重力测量中不可避免的现象。他受温度、气压、电磁力、弹性元件蠕变和弹性疲劳等不稳定因素的影响, 消除零漂保证重力仪的测量精度是一个复杂的问题^[1]。为了使弹簧减少非线性移动和降低漂移率, 主要采取的措施:一方面研制和选用高质量的弹簧, 提高重力仪整体制造的工艺水平; 另一方面采用恒温和自动温度补偿装置, 提供稳定的内在测量环境^{[2, 3]}。通过这些改进, 使弹簧的零漂变小并努力做到使它与时间保持线性关系, 就可以使用前、后校数据对中间的测量数据做零漂校正, 最后实现提高重力仪的测量精度水平 $\begin{matrix} ^{[45]} \end{matrix}$ 。GT航空重力仪结构、重力传感器设计以及测量实现过程虽然不同, 但航空重力仪的敏感单元与弹簧类似, 同样也存在这种零漂现象。

我国资源型航空重力测量使用的是引进俄罗斯GT-1A航空重力仪, 但由于GT-1A航空重力仪量程小、抗颠簸能力差等原因, 造成飞行生产效率低下。中国国土资源航空物探遥感中心通过与GT公司合作, 将目前现有的GT-1A型升级到GT-2A型, 升级后的航空重力仪具有更大的动态范围(± 1 g)和更低的噪声水平^[6]。GT航空重力仪均设计了二级温控系统, 温控精度不大于 0.01° C, 重力传感器处在一个精度更高的恒温环境中, 24 h漂移不大于5 mGal/day^[7]。GT航空重力仪通过重力传感器精密设计和高精度温控系统的使用, 控制了传感器大部分的非线性漂移, 使通用零漂改正方法在航空重力测量中变得可行。

航空重力仪内部温控精度虽然很高, 但是传感器单元受外界环境温度变化还是比较敏感, 尤其在夏、冬两季, 外界极端的高、低温度和剧烈的温差变化下, 温控温度发生细微的变化, 就会连锁反应到重力传感器敏感元件的测量中^{[8, 9]}。目前发现这种重力值变化与外界温度以及仪器内部多级温控之间都存在一定的规律。

笔者对传感器静态测量数据进行固体潮改正和零漂改正后, 使用一元线性回归方法对初步改正过的静态数据和仪器温控数据建立回归方程进行处理 $\begin{matrix} ^{[1013]} \end{matrix}$ 。这种方法研究了传感器测量值和温度之间的关系, 提高了处理航空重力仪静态数据的精度水平。笔者探讨了影响传感器测量精度的关键因素并改进了零漂改正方法, 对下一步实际应用拟合方法进行动态测量中的零漂改正建模研究, 具有很好的借鉴意义。

1 相关性分析方法原理

1.1 线性相关

统计学中常用相关系数r来衡量两个变量之间的线性相关的强弱, 当x_n不全为0, y_n也不全为0时, n=1, 2, …, N, 则两个变量的相关系数的计算公式为:

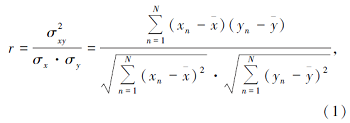
其中, r为变量y与x的相关系数(简称相关系数); $\begin{matrix} σ_{xy}^{2} \end{matrix}$ 为x_n与y_n的方差, σ _x、σ _y分别为x_n与y_n的标准差。当r为正数时, 表示变量x、y正相关; r取值0.8~1, 证明两变量之间正相关性极强; 取值0.6~0.8, 相关性很强; 取值0.4~0.6, 相关性中等; 取值0.2~0.4, 相关性弱; 取值0~0.2, 相关性极弱或无关。当r为负数时, 表示两个变量x、y负相关。

1.2 回归分析

对于变量y和x通过线性相关检验, 具有线性相关关系, 则可以建立一元线性回归方程:

$\begin{matrix} \dot{y} = a + bx 。 (2) \end{matrix}$

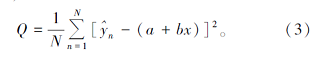
如何定量评价x和 $\begin{matrix} \dot{y} \end{matrix}$ 的相近程度, 可以用最小二乘逼近拟合来说明。逼近 $\begin{matrix} \dot{y} \end{matrix}$ , 它们的数据点为n=1, 2, …, N, 其产生的均方差为:

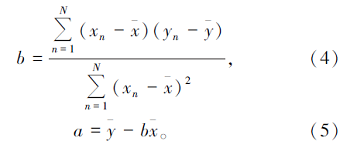
为使Q达到最小, a和b需满足 $\begin{matrix} \frac{\partial Q}{\partial a} \end{matrix}$ =0和 $\begin{matrix} \frac{\partial Q}{\partial b} \end{matrix}$ =0, 由此解得回归系数b和截距a:

2 重力静态数据预处理

GT-2A航空重力仪采集的静态数据为重力仪非作业时期的仪器监控数据, 采样间隔为60 s。案例数据挑选在冬季(2013年12月), 辽宁省辽阳市室外直升机临时停机坪环境下记录的重力仪R& T文件(重力传感器、陀螺等器件的记数和各部件温度监测的数据文件), 从中截取了24 h数据, 为了分析航空重力仪传感器测量数据和腔体温度数据的相关性, 首先对重力静态数据做如下预处理。

2.1 固体潮改正

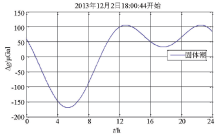
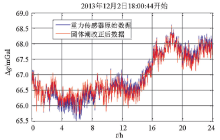
由于GT航空重力仪动态测量内符合精度为 0.6 mGal, 远大于固体潮的极大值约0.16 mGal(图1), 因固体潮对航空重力测量影响有限, 所以GT公司在系统设计时忽略了这项改正。笔者针对这一情况, 根据中国地质调查局发布的固体潮公式^[14], 编写改正模块对航空重力数据进行了固体潮改正。图2中重力传感器数据经固体潮改正后, 质量略有改善, 标准差精度从0.72 mGal提高到0.66 mGal。

	Figure Option View Download New Window
	图1 GT-2A重力数据对应时间的固体潮

	Figure Option View Download New Window
	图2 GT-2A静态数据固体潮改正

2.2 最小二乘零漂改正

静态数据经固体潮改正后, 数据零漂特征几乎没有被改变, 为了与仪器腔体内的温度做相关性分析, 还需要去除零漂现象。

此处的零漂改正方法使用常规公式, 根据i和j已知点, 推算n=1, 2, …, N, 所有点的零漂改正值, 公式如下:

$\begin{matrix} \begin{matrix} y_{n} = \frac{y_{i} - y_{j}}{x_{i} - x_{j}} x_{n} + b, (7) \\ b = y_{i} - \frac{y_{i} - y_{j}}{x_{i} - x_{j}} x_{i} 。 (8) \end{matrix} \end{matrix}$

如何选择已知i和j点, 地面重力和航空重力通常做法是通过前、后校数据获得。本试验数据为航空重力仪在停机坪测量的静态数据, 所测数据受环境温度变化的影响比较严重, 数据中伴随的扰动也较大, 这个扰动量甚至要大于数据的零漂趋势。在这种情况下, 如果选用首、尾位置在波动性较大的数据中做零漂改正就显得不太合理, 也必然会引入较大的改正误差, 此处提出使用最小二乘方法寻找比较合理的i和j数据点后, 再对数据进行线性零漂改正。

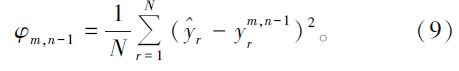
设i, j∈ [1, N], 分别作为第一和第二循环滑动点位置, 去除重复点位后, 通过上述公式首先计算出N× (N-1)种组合的斜率k_m_,_n-₁和截距b_m_,_n-₁, 再计算每组斜率和截距对应的零漂值 $\begin{matrix} y_{r}^{m, n - 1} \end{matrix}$ , 其中数据点m、n、r=1, 2, …, N, 计算均方差为:

使φ _m_,_n-₁达到最小, 确定最小二乘斜率k_m_,_n-₁, 通过式(7)计算获得零漂改正后的重力值 $\begin{matrix} {\dot{y}}_{r} \end{matrix}$ 。如图3中, 改正过后的静态重力值已经去除了零漂趋势项, 标准差精度也从0.66 mGal提高到0.40 mGal。

	Figure Option View Download New Window
	图3 GT-2A静态数据零漂改正

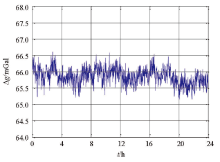
如果直接进行首、尾点零漂改正的精度为0.42 mGal, 改正后也会使首、尾数据点相等而拉成水平走势。使用最小二乘零漂改正的精度略有改善, 但这不是主要的, 最终目的是为了使这组数据与仪器腔体温度变化呈现出更好的一致性。假如静态数据做完固体潮改正后, 与温度走势吻合度较好, 也可以跳过最小二乘零漂改正这一步。

3 相关性分析实例计算

3.1 线性相关分析

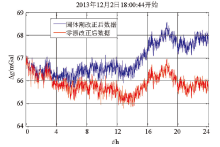
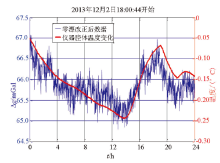
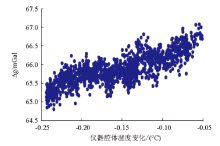
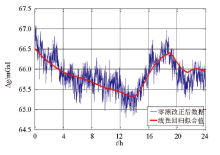
从图4中, 可以观察到预处理后的静态数据与航空重力仪腔体温度变化之间的曲线走势很紧密, 从这两个物理量的散点分布(图5)可以看出静态数据与重力仪腔体温度之间存在相关性。

	Figure Option View Download New Window
	图4 零漂改正后静态数据与仪器腔体温度对比

	Figure Option View Download New Window
	图5 静态数据与仪器腔体温度散点分布

根据式(1)计算获得相关系数r为0.80, 两变量之间具有极强的正相关性。同时, 静态数据与航空重力仪传感器内部温度(二级温控)也进行了相关性分析, 得出的相关系数r为0.74。通过相关性检验, 选择与环境温度更接近的航空重力仪腔体温度参数, 并建立线性回归方程。

3.2 回归模型计算

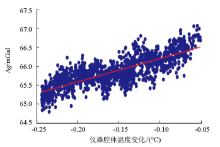
经分析发现, 改正后静态数据与仪器腔体温度存在线性相关性, 将静态数据设为因变量y, 重力仪腔体温度为自变量x, 建立一元回归模型, 见式(2)。又通过式(4)、(5)分别获得回归系数b为6.16, 常数a为66.82(图6), 回归方程为:

$\begin{matrix} y = 6.16 x + 66.82 。 (10) \end{matrix}$

	Figure Option View Download New Window
	图6 静态数据与仪器腔体温度关系图(红线为回归方程)

3.3 静态数据相关性改正

建立回归方程后, 以仪器腔体温度作为因变量输入到回归方程(10)中, 获得重力数据的线性回归拟合值(图7)。再把拟合重力值去均值, 获得重力相关性改正值, 用作零漂改正中的相关性改正项, 得到静态数据改正后的最终结果(图8)。标准差精度从零漂改正后0.40 mGal提升到0.24 mGal。

	Figure Option View Download New Window
	图7 零漂改正后静态数据与线性回归拟合值

	Figure Option View Download New Window
	图8 静态数据相关性改正后最终结果

4 多组实例数据分析

表1为GT-2A(SN15)航空重力仪分别在3个测区的停机坪环境下记录的重力仪R& T文件, 分析了历时1年多典型季节下的10组静态数据。

表中重力仪24 h的静态数据原始精度很不稳定, 最大1组达到1.22 mGal, 远大于GT-2A静态噪声水平(4 h内测试精度不大于0.4 mGal), 仅有1组符合这个指标。通过固体潮改正、零漂改正和相关性改正后, 所有数据的精度水平有了较大的提高, 除1组数据不符合外, 其余9组数据全部符合这个指标。证明相关性分析方法应用于航空重力仪零漂改正中具有很好的效果。

表1显示, 重力仪传感器静态数据与腔体温控数据的相关性强弱与所处季节以及腔体温度峰峰值变化密切相关, 尤其是夏季和初秋, 重力仪在没有降温和恒温措施的条件下, 经受沙漠极端气候的温差变化, 静态数据与腔体温度的相关性变弱。而重力仪在采取保温措施的冬季、初春和深秋, 仪器内部的腔体温度受到环境温度变化的影响较小, 静态数据与温度之间的相关性也变强。

表1 24小时静态数据相关性改正统计

试验号	机场地点	日期	起始时间	$\begin{matrix} \frac{原始精度}{mGal} \end{matrix}$	$\begin{matrix} \frac{固体潮改正}{mGal} \end{matrix}$	$\begin{matrix} \frac{零漂改正}{mGal} \end{matrix}$	$\begin{matrix} \frac{相关性改正}{mGal} \end{matrix}$	与腔体温度相关性	腔体温度峰峰值变化/(℃)	回归系数 b	常数 a	备注
1	辽宁辽阳	2013.12.02	18:00:44	0.72	0.66	0.40	0.24	0.80	0.19	6.16	66.82
2	新疆库尔勒	2014.01.26	7:20:54	1.22	1.24	0.76	0.26	0.94	0.36	8.50	-250.57	关机转场
3	新疆库尔勒	2014.04.14	7:00:08	1.21	1.22	1.44	0.49	0.94	0.31	12.78	-233.62
4	新疆库尔勒	2014.05.16	6:00:37	0.48	0.52	0.42	0.22	0.86	0.38	2.22	-229.70
5	新疆阿克苏	2014.07.01	9:20:08	0.32	0.31	0.21	0.16	0.63	0.45	0.87	-359.82	关机转场
6	新疆阿克苏	2014.08.07	5:34:00	0.86	0.82	0.28	0.23	0.58	0.54	0.96	-368.41
7	新疆阿克苏	2014.09.20	6:43:00	0.40	0.42	0.33	0.25	0.65	0.44	1.61	-354.27
8	新疆阿克苏	2014.10.17	0:00:34	0.42	0.43	未改	0.18	0.90	0.30	3.76	-353.17
9	新疆阿克苏	2014.12.21	0:00:25	0.42	0.37	未改	0.22	0.81	0.26	3.46	-344.94
10	新疆阿克苏	2015.02.14	21:00:38	0.45	0.40	0.34	0.22	0.78	0.38	2.10	-347.98	关机

表1 24小时静态数据相关性改正统计

10组数据中相关性参数的回归系数b和常数a, 也揭示了一定的规律性。回归系数b的范围在0.87~12.78之间, 平均值4.24, 去掉两组最大和最小值数据后平均值为3.60; 回归系数b在夏季要比其余季节偏小。常数a与仪器零点漂移和航空重力仪转场作业具有一定的关联性, 最主要的影响因素为作业地点绝对重力场值的改变。

5 结论

笔者采用相关性分析方法对航空重力仪静态数据中的扰动量与仪器腔体内温度数据进行了研究, 获得两者之间具有较强的相关性, 并建立了合理可靠的回归方程, 最终改正后的重力静态数据标准差精度有了很大的提高。这对深入理解传感器零漂改正处理方法和应用于动态测量数据中的零漂改正预测研究具有实际意义。

航空重力仪结构复杂, 实际的测量环境也是变化无常。一方面二级温控系统控制了传感器大部分的非线性漂移, 但也不排除偶发的非线性突变现象; 另一方面, 重力传感器的零漂现象不仅受温度影响, 还可能受气压、机载振动等因素的干扰。如何建立一个更加合理的多元线性回归模型或者非线性回归模型, 还有待于进一步开展深入研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005. [本文引用:1]
[2]	Becker D, Nielsen J E, Ayres-Sampaio D, et al. Drift reduction in strapdown airborne gravimetry using a simple thermal correction[J]. Journal of Geodesy, 2015, 89(11): 1133-1144. [本文引用:1]
[3]	Cao J, Wang M, Cai S, et al. Optimized design of the SGA-WZ strapdown airborne gavimeter temperature control system[J]. Sensors, 2015, 15(12): 29984-29996. [本文引用:1]
[4]	邢乐林, 李辉, 夏正超, 等. CG-5重力仪零漂特性研究[J]. 地震学刊, 2010, 32(3): 369-373. [本文引用:1]
[5]	袁果田, 张勇军. 拉科斯特型重力仪的零漂特征及其处理方法[J]. 地震学刊, 1995(4): 45-50. [本文引用:1]
[6]	Olson D. GT-1A and GT-2A airborne gravimeters: Improvements in design and processing from 2003 to 2010[J]. Airborne Gravity 2010: 152-171. [本文引用:1]
[7]	熊盛青, 周锡华, 郭志宏, 等. 航空重力勘探理论方法及应用[M]. 北京: 地质出版社, 2010. [本文引用:1]
[8]	赵晓辉, 伊国兴, 王常虹. 硅微陀螺温度漂移补偿研究[J]. 传感器与微系统, 2008, 27(10): 48-50. [本文引用:1]
[9]	秦伟, 苑伟政, 常洪龙, 等. 基于模糊逻辑的MEMS陀螺零漂温度补偿技术[J]. 弹箭与制导学报, 2011, 31(6): 19-23. [本文引用:1]
[10]	谢光军, 胡茑庆, 秦国军. 涡轮泵振动参数与统计特征量的线性相关性分析[J]. 推进技术, 2005, 26(6): 540-547. [本文引用:1]
[11]	范正国, 刘前坤, 黄旭钊, 等. 自适应重磁对应分析[J]. 吉林大学学报: 地球科学版, 2012, 42(6): 1903-1911. [本文引用:1]
[12]	刘彦华, 陈宗刚, 欧阳长亮. 重磁异常对应分析在相山地区的应用[J]. 物探与化探, 2008, 32(6): 586-589. [本文引用:1]
[13]	刘燕戌, 李文勇, 徐剑春. 航空重磁异常相关性分析方法及其应用[J]. 物探与化探, 2012, 36(5): 783-787. [本文引用:1]
[14]	中华人民共和国地质矿产部. 中华人民共和国地质矿产行业标准DZ/T 0171-1997 《大比例尺重力勘探规范》[S]. 1997. [本文引用:1]

2005

0.0

... 他受温度、气压、电磁力、弹性元件蠕变和弹性疲劳等不稳定因素的影响,消除零漂保证重力仪的测量精度是一个复杂的问题^[1] ...

2015

0.0

... 另一方面采用恒温和自动温度补偿装置,提供稳定的内在测量环境^[2,3] ...

2015

0.0

... 另一方面采用恒温和自动温度补偿装置,提供稳定的内在测量环境^[2,3] ...

2010

0.0

2010

0.0

... 1 g)和更低的噪声水平^[6] ...

2010

0.0

... C,重力传感器处在一个精度更高的恒温环境中,24 h漂移不大于5 mGal/day^[7] ...

2008

0.0

... 航空重力仪内部温控精度虽然很高,但是传感器单元受外界环境温度变化还是比较敏感,尤其在夏、冬两季,外界极端的高、低温度和剧烈的温差变化下,温控温度发生细微的变化,就会连锁反应到重力传感器敏感元件的测量中^[8,9] ...

2011

0.0

2005

0.0

2012

0.0

2008

0.0

2012

0.0

1997

0.0

... 笔者针对这一情况,根据中国地质调查局发布的固体潮公式^[14],编写改正模块对航空重力数据进行了固体潮改正 ...