航空重力仪减振系统振动研究

引用本文

屈进红, 周锡华, 姜作喜, 王蓬, 高维. 航空重力仪减振系统振动研究[J]. 物探与化探, 2016,40(4): 831-837.
QU Jin-Hong, ZHOU Xi-Hua, JIANG Zuo-Xi, WANG Peng, GAO Wei. A study of the vibration for the airborne gravimeter vibration reduction system[J]. Geophysical and Geochemical Exploration, 2016,40(4): 831-837.
Doi:10.11720/wtyht.2016.4.31 复制到剪切板

Permissions

《物探与化探》编辑部所有

航空重力仪减振系统振动研究

屈进红^1,², 周锡华^1,², 姜作喜^1,², 王蓬^1,², 高维¹

1.中国国土资源航空物探遥感中心,北京 100083

2.国土资源部航空地球物理与遥感地质重点实验室,北京 100083

作者简介: 屈进红(1981-),男,江苏无锡人,工程师,2007年毕业于成都理工大学地球物理系固体地球物理学专业,现主要从事航空地球物理探测技术、数据处理、航空重力减振技术及相关技术的应用研究工作。

收稿日期: 2015-12-15

基金: 国家高技术研究发展计划(“863”计划)“新型高精度航空重力勘查系统研制”项目(2013AA063902); 中国地质调查局“航空重力测量技术规范”项目(12120115054801)

摘要

航空重力减振系统是有效减弱机载环境下高频振动的主要途径,从而提高航空重力的测量精度。因此,设计减振系统的首要问题是设定其合理的刚度、阻尼和质量等重要的特性参数。笔者通过建立航空重力仪两种减振系统类型运动微分方程,经过理论和实例探讨了减振系统模型,旨在深入了解航空重力减振系统的减振规律,为其特性参数设计提供理论依据。

关键词: 航空重力; 高频振动; 减振系统; 微分方程

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)04-0831-07 doi: 10.11720/wtyht.2016.4.31

A study of the vibration for the airborne gravimeter vibration reduction system

QU Jin-Hong^1,², ZHOU Xi-Hua^1,², JIANG Zuo-Xi^1,², WANG Peng^1,², GAO Wei¹

1.China Aero Geophysical Survey and Remote Sensing Center for Land and Resources,Beijing 100083,China

2.Key Laboratory of Airborne Geophysics and Remote Sensing Geology,Ministry of Land and Resources,Beijing 100083,China

Abstract

The airborne gravity vibration reduction system is an effective way to attenuate high frequency vibration in the airborne environment,thus improving measurement accuracy of aviation gravity.Therefore,the primary problem in the design of the vibration reduction system is to set up such important parameters as reasonable stiffness,damping,and quality.The authors established differential equations of motion for two types of vibration reduction system of airborne gravimeter.With theoretical and investigate instances,the authors discussed vibration reduction system model,with the purpose of in-depth understanding of the law of airborne gravity vibration reduction system and providing the necessary theoretical support for its parameter design.

Keyword: airborne gravity; high-frequency vibration; vibrationreduction reduction system; differential equations

Show Figures

机载环境下, 由于飞机发动机等引起的高频扰动加速度往往是所测重力异常信号的成百上千倍, 同时高频振动信号也会使导航解算误差增大, 这些噪声单靠数字滤波是不能完全消除的^[1]。为了提高航空重力测量的精度和分辨率, 需要利用减振系统来减弱高频加速度的影响。

目前, 实用型航空重力仪主要有3种类型^[2]:二轴阻尼惯性稳定平台型航空重力仪, 以美国LaCoste& Romberg公司Ⅱ 、Ⅲ 型海/空重力仪(最近几年又推出TAGS系列)为代表; 三轴惯性稳定平台型航空重力仪, 以俄罗斯GT-1A/GT-2A^[3](动态范围± 1g)和加拿大Sander公司的AIRGrav航空重力仪为代表; 惯性导航系统INS与DGPS结合的捷联式航空重力仪, 没有物理平台, 以加拿大卡尔加里大学的SIGS系统和德国的SAGS系统^[4]为代表。我国国防科技大学最新研制的SGA-WZ捷联式航空重力仪已经达到同类产品的国际先进水平^[5]。俄罗斯GT-X捷联式航空重力仪设计指标与GT-1A/GT-2A同一精度水平, 一直处在实验阶段。这些航空重力测量系统无一例外, 均设计了复杂的减振系统隔离机载环境下的激励振动。

二轴阻尼惯性稳定平台TAGS系统和三轴惯性稳定平台GT-1A系统的减振系统均由两级减振器组成:第一级用来隔离飞机底板和重力仪底座之间的振动能量传递; 第二级隔离重力仪测量主体与重力仪底座的振动^[6]。而捷联式航空重力仪, 与平台式航空重力仪比较, 设计相对简单, 不需要为物理平台做减振, 直接把敏感测量部件安装在设有一级减振器的仪器基座上。

国内外学者对机载设备振动进行了不少深入研究^{[7, 8]}, 但很少有人针对航空重力减振系统进行系统研究。笔者之前对GT-1A航空重力仪在机载环境下进行了减振系统的振动测试^[9], 缺少对减振系统进行深入探讨。笔者依据航空重力仪两种减振系统类型, 分别建立了激励环境下的运动微分模型, 探讨减振系统的工作机制, 旨在掌握航空重力仪减振系统的减振规律, 为研制国产资源型航空重力仪做好相关技术的储备。

1 捷联式减振系统

捷联式航空重力仪因为没有稳定平台, 惯性敏感器(陀螺、加速度计和重力传感器)测量既需要一个相对的稳固平台, 又需要增加一定阻尼来克服飞机振动对他的干扰。虽然只需设计一级减振, 但是要设计一个合理的减振基座也是一个复杂问题, 诸如匹配减振基座的设计、系统内惯性敏感器的特性以及主体平台干扰特性的范围和频率都要进行深入的研究和匹配。

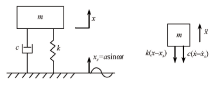
振动中许多复杂问题一般通过简化, 选用一级减振模型, 即单自由度系统的振动理论就能得到满意的结果。在揭示单自由度系统的振动规律、特点的同时, 也为进一步研究复杂振动系统奠定理论基础。下面以一级减振系统为模型, 支座在简谐运动作用下引起的强迫振动。

	Figure Option View Download New Window
	图1 支座作简谐运动引起的振动及力学分析

图1根据力学分析, 建立系统振动微分方程为

$\begin{matrix} m \overset{\cdot \cdot}{x} + c \overset{\cdot}{x} + kx = c {\overset{\cdot}{x}}_{s} + k x_{s}, (1) \end{matrix}$

其中, m为质量块的质量, k为线性弹簧刚度, c为阻尼器的粘滞阻尼系数, $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ 为质量块加速度, $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ 、 $\begin{matrix} {\overset{\cdot}{x}}_{s} \end{matrix}$ 分别为质量块速度和支座作用下的速度, x、x_s分别为质量块位移和支座作用下的位移。

支撑简谐运动x_s=asinω t, 其中:a为振幅, ω 为角频率, t为时间。把x_s代入式(1)可得

$\begin{matrix} m \overset{\cdot \cdot}{x} + c \overset{\cdot}{x} + kx = caωcosωt + kasinωt 。 (2) \end{matrix}$

式(2)表明:由于支撑运动使质量m受到两部分激振力, 一部分由弹簧传递过来的激振力kx_s; 另一部分由阻尼器传递过来的激振力c $\begin{matrix} {\overset{\cdot}{x}}_{s} \end{matrix}$ , 相位比x_s超前π /2。系统的稳态响应如下:

$\begin{matrix} \begin{matrix} x(t)= \frac{a}{\sqrt[]{(1 - λ^{2})^{2} + {(2 ξλ)}^{2}}} \cdot [\sin (ωt - φ_{1}) + 2 ξλcos (ωt - φ_{1})] \\ = Xsin (ωt - φ), (3) \end{matrix} \end{matrix}$

其中, ω _n= $\begin{matrix} \sqrt[]{\frac{k}{m}} \end{matrix}$ 为无阻尼固有圆频率, ξ = $\begin{matrix} \frac{c}{2 m ω_{n}} \end{matrix}$ = $\begin{matrix} \frac{c}{2 \sqrt[]{mk}} \end{matrix}$ 为阻尼比, λ =ω /ω _n为频率比, 得出振动响应幅值X和响应与激励的相位差φ 分别为:

$\begin{matrix} \begin{matrix} X = a \sqrt[]{\frac{1 + {(2 ξλ)}^{2}}{(1 - λ^{2})^{2} + {(2 ξλ)}^{2}}}, (4) \\ φ = \arctan \frac{2 ξ λ^{3}}{1 - λ^{2} + {(2 ξλ)}^{2}}, (5) \end{matrix} \end{matrix}$

放大因子β =X/a, 即

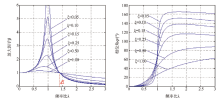
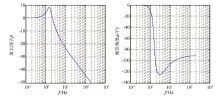
$\begin{matrix} β = \sqrt[]{\frac{1 + {(2 ξλ)}^{2}}{(1 - λ^{2})^{2} + {(2 ξλ)}^{2}}} 。 (6) \end{matrix}$

图2揭示了捷联式一级减振系统的减振规律, 幅频和相频曲线突变的位置为系统的固有频率共振频率位置, 随着阻尼比ξ 增大, 幅频曲线固有频率的共振逐渐被压制, 相频曲线同时也变缓; 当频率比λ > $\begin{matrix} \sqrt[]{2} \end{matrix}$ 倍, 系统就处在减振区, 随着λ 增大, 减振效果就会越来越好, 工程中λ 一般取2.5~5^[10]; 阻尼比ξ 越小, 在减振区减振效果就会越好, 但是固有频率频段强迫振动反而被放的更大。

可以得出结论:①设计一级减振系统, 在选择减振器的时候, 应该掌握机载环境的振动频率, λ 合理取值在2.5~5之间; ②减振器阻尼比ξ 并不是设计的越小越好, 高频区隔振固然需要, 同时应顾虑到在共振区内被放大的强迫振动, 如果控制不当, 反而影响到航空重力仪的测量精度。

	Figure Option View Download New Window
	图2 一级减振系统在简谐力作用下的幅频、相频特性曲线

2 平台式减振系统

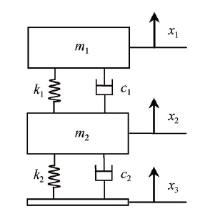
GT-1A/2A与TAGS航空重力仪都设有稳定平台, 为保证稳定平台上重力传感器的高精度测量, 设计了复杂的两级减振系统, 即属于二自由度系统^{[7, 11, 12]}。图 3为二自由度系统的力学模型, 设隔振对象的质量为m₁, 隔振系统的中间质量为m₂, 两个隔振器的刚度系数分别为k₁和k₂, 阻尼系数分别为c₁和c₂。基座铅垂位移为x₃, 隔振对象和中间质量的铅垂位移为x₁和x₂。

	Figure Option View Download New Window
	图3 支座位移激励下的二自由度系统

	Figure Option View Download New Window
	图4 二自由度系统分解力学分析

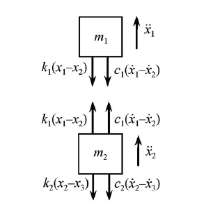
图4中, 对二自由度体进行分解和力学分析, 则系统的振动微分方程为:

$\begin{matrix} \begin{matrix} m_{1} {\overset{\cdot \cdot}{x}}_{1} + c_{1} ({\overset{\cdot}{x}}_{1} - {\overset{\cdot}{x}}_{2}) + k_{1} (x_{1} - x_{2}) = 0, (7) \\ m_{2} {\overset{\cdot \cdot}{x}}_{2} + (c_{1} + c_{2}) {\overset{\cdot}{x}}_{2} - c_{1} {\overset{\cdot}{x}}_{1} + (k_{1} + k_{2}) x_{2} - \\ k_{1} x_{1} - c_{2} {\overset{\cdot}{x}}_{3} - k_{2} x_{3} = 0, (8) \end{matrix} \end{matrix}$

写成矩阵形式便有

$\begin{matrix} \begin{matrix} [\begin{matrix} m_{1} & 0 \\ 0 & m_{2} \end{matrix}] [\begin{matrix} {\overset{\cdot \cdot}{x}}_{1} \\ {\overset{\cdot \cdot}{x}}_{2} \end{matrix}] + [\begin{matrix} c_{1} & - c_{1} \\ - c_{1} & c_{1} + c_{2} \end{matrix}] [\begin{matrix} {\overset{\cdot}{x}}_{1} \\ {\overset{\cdot}{x}}_{2} \end{matrix}] + \\ [\begin{matrix} k_{1} & - k_{1} \\ - k_{1} & k_{1} + k_{2} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \end{matrix}] = [\begin{matrix} 0 & 0 \\ c_{2} & k_{2} \end{matrix}] [\begin{matrix} {\overset{\cdot}{x}}_{3} \\ x_{3} \end{matrix}] 。 (9) \end{matrix} \end{matrix}$

对上面方程两边分别进行拉普拉斯变换, 并整理得到隔振支座到对象m₁位移X₁的解析表达式

$\begin{matrix} X_{1} = \frac{X_{3} (b_{2} s^{2} + b_{1} s + b_{0})}{a_{4} s^{4} + a_{3} s^{3} + a_{2} s^{2} + a_{1} s + a_{0}}, (10) \end{matrix}$

其中, X₃为基座激励位移u的拉氏变换, 各系数分别为:

$\begin{matrix} \begin{matrix} a_{4} = m_{1} m_{2}, a_{3} = m_{1} (c_{1} + c_{2}) + m_{2} c_{1}, \\ a_{2} = m_{1} (k_{1} + k_{2}) + m_{2} k_{1} + c_{1} c_{2}, \\ a_{1} = k_{1} c_{2} + k_{2} c_{1}, a_{0} = k_{1} k_{2}, b_{2} = c_{1} c_{2}, \\ b_{1} = k_{1} c_{2} + k_{2} c_{1}, b_{0} = k_{1} k_{2}, \end{matrix} \end{matrix}$

二自由度系统支座位移下的放大因子β ₁₃可表示成

$\begin{matrix} β_{13} = \frac{X_{1}}{X_{3}} = \frac{b_{2} s^{2} + b_{1} s + b_{0}}{a_{4} s^{4} + a_{3} s^{3} + a_{2} s^{2} + a_{1} s + a_{0}}, (11) \end{matrix}$

同时可以得到, 对象m₂到m₁的位移放大因子β ₁₂和支座到m₂位移放大因子β ₂₃:

$\begin{matrix} \begin{matrix} β_{12} = \frac{X_{1}}{X_{2}} = \frac{c_{1} s + k_{1}}{m_{1} s^{2} + c_{1} s + k_{1}}, (12) \\ β_{23} = \frac{X_{2}}{X_{3}} = \frac{(m_{1} c_{2}) s^{3} + (c_{1} c_{2} + m_{1} k_{2}) s^{2} + b_{1} s + b_{0}}{a_{4} s^{4} + a_{3} s^{3} + a_{2} s^{2} + a_{1} s + a_{0}} 。 (13) \end{matrix} \end{matrix}$

3 TAGS减振系统实例分析

3.1 减振系统传递率分析

上述二自由度系统在支座激励下, 通过建立方程推导出了位移传递率, 即两级减振系统在激励下的放大因子理论公式。TAGS航空重力仪为LaCoste& Rombery Ⅱ 、Ⅲ 型海/空重力仪升级版本, 除质量块有变动外, 减振材料未曾改变。

通过称重和文献^[7]获知减振系统中各部分的质量、刚度和阻尼参数:传感器与万向节m₁=50.45 kg; 粘弹性减振绳刚度k₁=4 826.4 N/m, 阻尼c₁=206 N· s/m; 框架及周围电子设备m₁=50.45 kg, m₂=56.1 kg; 气压减振器刚度k₂=26 500 N/m, 阻尼c₂=1 000 N· s/m。代入式(11)~(13)可获得系统各个部分之间的位移激励下的放大因子β ₁₂、β ₂₃、β ₁₃, 以及幅频、相频特性曲线:

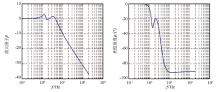
通过求解式(14)~(16)可得β ₁₂、β ₂₃、β ₁₃放大因子的特征根。β ₁₂存在2个共轭复根的特征根, -2.0415± 9.5657i; β ₂₃、β ₁₃特征根一致, 存在4个特征根, -1.6354± 8.7103i、-11.1546± 21.2349i。根据特征根解s_{1, 2}=(-ξ ± $\begin{matrix} \sqrt[]{ξ^{2} - 1} \end{matrix}$ )ω _n可以计算航空重力系统对象m₂到m₁的固有频率和阻尼比为1.52 Hz和20.9%; 对象m₃到m₂和对象m₃到m₁的固有频率和阻尼比分别为 1.39 Hz、18.45%, 3.38 Hz、46.5%。

	Figure Option View Download New Window
	图5 位移2到位移1的幅频、相频特性曲线

	Figure Option View Download New Window
	图6 位移3到位移2的幅频、相频特性曲线

	Figure Option View Download New Window
	图7 位移3到位移1的幅频、相频特性曲线

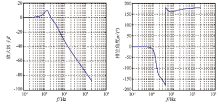
固有频率与阻尼比的计算结果与图7中位移幅频、相频特性曲线吻合。图7中幅频曲线中, 可以获知第1阶固有频率1.39 Hz, 隔振对象的位移传递率, 即放大因子呈放大作用。从2.2 Hz开始位移传递表现出衰减作用, 在第2阶固有频率3.38 Hz, 由于其阻尼值较大, 图7中放大因子曲线上放大作用不太明显; 而图6中放大因子曲线中的两阶固有频率非常清晰。

TAGS减振系统从图7理论模型得出截止频率约为2.2 Hz, 但是实际上在两级减振系统中很难达到, 一般截止频率要求为5~10 Hz。

理论上, 对于一级隔振装置一般可以衰减40~60 dB, 但实际上很少能衰减20 dB以上。即使采用了双层减振装置, 在高频区仍难以达到理想减振效果, 且频率越高实际与预期的差值就越大^[13]。因为减振系统振动分析建立在一种简化后的理想模型, 实际的系统结构之间不够刚性以及质量不够集中, 减振器也可能不理想等情况存在。

3.2 k、c、m对减振系统振动传递率的影响

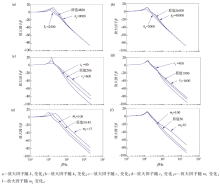
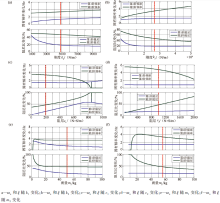
根据式(11)和式(16), 在改变系统的特性参数刚度k、阻尼c和质量m情况下, 系统位移放大因子β ₁₃随之发生改变(图8)。放大因子代表系统位移传递率, 值越小则证明系统的隔振能力就越强。

	Figure Option View Download New Window
	图8 TAGS航空重力减振系统振动传递率曲线

图8a、b表示系统第1阶和第2阶固有频率位置放大因子分别被刚度k₁和k₂所控制, 隔振能力会随着刚度的增大而变弱, 而随着刚度的变小而变强。图8c、d表示系统第1阶和第2阶固有频率位置放大因子分别被阻尼c₁和c₂所控制, 控制区域的隔振能力随着阻尼增大而得到增强, 但是在高频区的隔振能力反而变得更弱。图8e、f表示增大m₁和m₂, 可以分别使系统第1阶和第2阶的固有频率和阻尼减小, 虽然阻尼减小的频率位置隔振能力变弱, 但是在整个频域内的隔振能力却得到了增强。

TAGS航空重力减振系统的振动传递率与系统的刚度k、阻尼c和质量m关系非常密切(图8), TAGS航空重力两级减振系统的刚度k₁和k₂, 只要固有频率位置的隔振效率能被接受, 刚度越小隔振效果就越好; 同样, 在固有频率位置的隔振效率允许的情况下, 系统阻尼c₁和c₂越小隔振效率越高; 质量刚刚相反, m₁和m₂越大隔振效果越理想, 固有频率位置与刚度和阻尼的处理方法一致。

因此, 以两级减振系统在固有频率位置被放大的振动激励没有影响到航空重力仪的测量精度为原则, 减振系统中刚度k₁、k₂和阻尼c₁、c₂越小, 质量m₁、m₂越大, 减振系统的减振效果越理想。

3.3 特性参数k、c、m与ω _n、ξ 模拟分析

已经得知刚度、阻尼和质量块的改变, 减振系统传递率就会发生改变。针对TAGS减振系统特性参数k、c、m的模拟变化, 得出系统固有频率ω _n和阻尼比ξ 随之发生改变的历程。图9和表1的分析结果中红色虚线为TAGS系统实际参数下的固有频率和阻尼比。

	Figure Option View Download New Window
	图9 ω _n和ξ 随k₁、k₂、c₁、c₂、m₁、m₂变化

表1 TAGS减振系统固有频率、阻尼比随特性参数变化的评价

4 结论

笔者针对航空重力仪两种不同的减振系统类型, 分别建立了两种减振系统在激励环境下的运动微分方程模型, 经过理论和对实例TAGS减振系统的探讨得出以下结论:①捷联式一级减振系统所处的机载激振频率只要大于系统固有频率的 $\begin{matrix} \sqrt[]{2} \end{matrix}$ 倍, 就会有隔振效果; ②捷联式一级减振系统在共振频段的强迫振动只要不影响航空重力测量精度的前提下, 减振器的阻尼比ξ 设计的越小, 整体的隔振效率就越高; ③平台式两级减振系统在固有频率位置被放大的振动能量以不影响航空重力仪的测量精度为原则, 减振系统中刚度k₁、k₂和阻尼c₁、c₂越小, 质量m₁、m₂越大, 对应减振系统整体的减振效果就越理想; ④平台式减振系统的1、2阶固有频率和阻尼比, 可以通过刚度k₁、k₂, 阻尼c₁、c₂和质量m₁、m₂等物理量设计来控制。

通过研究航空重力仪减振系统的振动问题、减振规律, 可以为航空重力仪减振系统设计提供重要的理论依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张开东. 基于SINS_DGPS的航空重力测量方法研究[D]. 长沙: 国防科技大学, 2007. [本文引用:1]
[2]	熊盛青, 周锡华, 郭志宏, 等. 航空重力勘探理论方法及应用[M]. 北京: 地质出版社, 2010. [本文引用:1]
[3]	Olson D. GT-1A and GT-2A airborne gravimeters: Improvements in design and processing from 2003 to 2010[J]. Airborne Gravity, 2010: 152-171. [本文引用:1]
[4]	Boedecker G, Stürze A. SAGS4-Strapdown airborne gravimetry system analysis[R]. Observation of the earth system from space, 2006. [本文引用:1]
[5]	Yang N H, Arne V O, Mei P W. SGA-WZ: A New Strapdown Airborne Gravimeter[J]. Sensors, 2012, 12: 9336-9348. [本文引用:1]
[6]	屈进红, 周锡华, 姜作喜, 等. 减振技术在航空重力测量系统中的应用[C]//中国地球物理(第29届年会), 2013. [本文引用:1]
[7]	Aliod D, Mann E, Halliday M. Lacoste and romberg air-sea gravity meter vibration tests[EB/OL]. http://www.lacost-eromberg.com/relativepapers.htm. [本文引用:3]
[8]	Meyer U, Boedecker G, Pflug H. Airborne navigation and gravimetry ensemble & laboratory Introduction and first airborne tests[R]. GFZ, 2003. [本文引用:1]
[9]	屈进红, 周锡华, 李冰, 等. 航空重力减振系统振动测试与分析[J]. 物探与化探, 2012, 36(6): 960-965. [本文引用:1]
[10]	马帅旗. 机载电子设备减振设计[J]. 噪声与振动控制, 2014, 34(2): 185-187. [本文引用:1]
[11]	闻邦椿, 刘树英, 陈照波, 等. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009. [本文引用:1]
[12]	李徳葆, 陆秋海. 工程振动试验分析[M]. 北京: 清华大学出版社, 2004. [本文引用:1]
[13]	朱石坚, 楼京俊, 何其伟, 等. 振动理论与隔振技术[M]. 长沙: 国防工业出版社, 2008. [本文引用:1]

2007

0.0

... 机载环境下,由于飞机发动机等引起的高频扰动加速度往往是所测重力异常信号的成百上千倍,同时高频振动信号也会使导航解算误差增大,这些噪声单靠数字滤波是不能完全消除的^[1] ...

2010

0.0

... 目前,实用型航空重力仪主要有3种类型^[2]:二轴阻尼惯性稳定平台型航空重力仪,以美国LaCoste#cod#x00026 ...

2010

0.0

... 三轴惯性稳定平台型航空重力仪,以俄罗斯GT-1A/GT-2A^[3](动态范围#cod#x000b1 ...

2006

0.0

... 惯性导航系统INS与DGPS结合的捷联式航空重力仪,没有物理平台,以加拿大卡尔加里大学的SIGS系统和德国的SAGS系统^[4]为代表 ...

2012

0.0

... 我国国防科技大学最新研制的SGA-WZ捷联式航空重力仪已经达到同类产品的国际先进水平^[5] ...

0.0

... 第二级隔离重力仪测量主体与重力仪底座的振动^[6] ...

0.0

... 国内外学者对机载设备振动进行了不少深入研究^[7,8],但很少有人针对航空重力减振系统进行系统研究 ...

... 2 平台式减振系统GT-1A/2A与TAGS航空重力仪都设有稳定平台,为保证稳定平台上重力传感器的高精度测量,设计了复杂的两级减振系统,即属于二自由度系统^[7,11,12] ...

... 通过称重和文献^[7]获知减振系统中各部分的质量、刚度和阻尼参数:传感器与万向节m₁=50 ...

2003

0.0

... 国内外学者对机载设备振动进行了不少深入研究^[7,8],但很少有人针对航空重力减振系统进行系统研究 ...

2012

0.0

... 笔者之前对GT-1A航空重力仪在机载环境下进行了减振系统的振动测试^[9],缺少对减振系统进行深入探讨 ...

2014

0.0

... 5~5^[10] ...

2009

0.0

2004

0.0

2008

0.0

... 即使采用了双层减振装置,在高频区仍难以达到理想减振效果,且频率越高实际与预期的差值就越大^[13] ...