引用本文
罗维斌, 李梅, 韩海涛, 高曙德. 一种物探仪器系统特性高精度标定方法[J]. 物探与化探, 2016,40(4): 816-819.
LUO Wei-Bin, LI Mei, HAN Hai-Tao, GAO Shu-De. A high accuracy calibration method for geophysical prospecting instrument system characteristics[J]. Geophysical and Geochemical Exploration, 2016,40(4): 816-819.
Doi:10.11720/wtyht.2016.4.28  
Permissions
Copyright©2016, 《物探与化探》编辑部
《物探与化探》编辑部 所有
一种物探仪器系统特性高精度标定方法
罗维斌1, 李梅2, 韩海涛1, 高曙德3
1.甘肃省有色地质调查院,甘肃 兰州 730000
2.中国地质大学(北京) 信息工程学院,北京 100083
3.中国地震局 兰州地震研究所,甘肃 兰州 730000
通讯作者: 李梅,女,博士,副教授。E-mail:maggielimei@163.com

作者简介: 罗维斌(1972-),男,博士,物探高级工程师,中南大学博士毕业,从事电磁法勘探方面的应用研究工作。E-mail:lwbcsu@163.com

收稿日期: 2016-02-24
基金: 国家自然科学基金“相关辨识技术在谱激电中的应用研究”项目(41374185); 国家自然科学基金项目(41174059); 甘肃省地震局科技发展野外站基金项目(2014Y03)联合资助
摘要

笔者提出了基于相关辨识的物探仪器系统特性标定方法,采用逆重复 M序列作为激发信号,向仪器测量通道输入编码电流,按一定的采样率,记录激发电流和仪器响应输出时间序列,采用循环互相关法获取仪器系统的频率响应。仿真计算结果表明采用编码源循环互相关法标定仪器系统特性,提高了系统频率特性的频率分辨率。多周期叠加能显著提高辨识精度,提高采样率也有助于提高辨识精度,但要与系统数据存贮能力相匹配。

关键词: 仪器标定; 逆重复 M序列; 循环互相关; 频率响应
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)04-0816-04 doi: 10.11720/wtyht.2016.4.28
A high accuracy calibration method for geophysical prospecting instrument system characteristics
LUO Wei-Bin1, LI Mei2, HAN Hai-Tao1, GAO Shu-De3
1.Gansu Nonferrous Geological Survey Institute,Lanzhou 730000,China
2.School of Information Engineering,University of Geosciences (Beijing),Beijing 100083,China
3.Lanzhou of institute of Earthquake Research,CEA,Lanzhou 730000,China
Abstract

The high accuracy calibration method for the system characteristics of geophysical prospecting instruments based on correlation identification is proposed in this paper.The inverse repeated M sequence is used as the excitation signal,the measurement channel of the instrument is disturbed with encoded input current,the excitation current and instrument response output in time series is recorded according to the same sampling rate,and then circular cross-correlation method is used to obtain the instrument system frequency response.The simulation results show that the frequency resolution of the instrument system is improved by using the method based on encoding source,the multi-period excitation can significantly improve the accuracy of identification,and the right sampling rate is also helpful to improving the accuracy of identification,but it should match with the system data storage capacity.

Keyword: instrument calibration; inverse repeated M sequence; circular cross correlation; frequency response

地球物理勘查工作是一种利用仪器设备在地表或井中观测各类地球物理场的分布, 来获得地下地质体的分布的物理勘探方法, 他是一种基于观测的科学[1]。工作流程主要是根据勘查区物性条件, 选择好方法及观测仪器, 进行野外数据采集, 对数据处理并反演, 结合已知地质信息对反演结果进行合理地质解释, 必要时要投入多种方法进行综合勘查。电磁法勘查技术是电法中最活跃的分支之一, 基于编码源的抗干扰仪器也已开始实用化 29。

电磁法仪器在电磁法勘查中扮演重要角色, 仪器性能优劣直接影响勘查效果。目前, 国内大深度电磁法勘查仪器系统以国外仪器为主, 如V8、GDP32等。国内科研院所也在积极研发国产的电磁法工作站, 如中科院地质与地球物理研究所研制的SEP电磁系统[10], 中南大学广域电磁法观测系统[11], 湖南强军科技有限公司研发的精密激电仪器[12]等。观测方法已向阵列式观测方向发展, 提高了观测效率和观测精度。

阵列式观测的一个前提是所投入的采集设备有较好的一致性, 也就是各台观测仪器系统性能一致, 这在硬件设计上技术要求是很高的。解决的办法是对仪器系统进行标定, 获得每台仪器的系统性能频率响应, 在数据处理中消除仪器本身的响应, 而得到待探测大地本身的一致响应。对于仪器标定目前的常规做法是扫频法, 设定频率表, 按频率表逐频产生正弦波激励信号, 测量仪器的频率响应, 标定时间长且精度不太高。刘立超介绍了一种利用逆重复M序列的仪器标定方法, 测试结果显示比扫频法有更高的标定效率和精度[13]。

笔者提出一种新的获取观测仪器频率响应的方法并已申报专利[14]。利用逆重复M序列为信号源, 同步记录激励电流信号和仪器系统响应信号, 采用循环互相关法获得系统的频率响应。并通过仿真, 讨论了测量叠加周期以及采样率等参数对标定结果的影响。仿真结果表明该方法有较高的频率分辨率及抗干扰能力。

1 原理和方法

采用PRBS或逆重复M序列为激励信号波形, 利用互相关法辨识待辨识系统的频率响应是一种应用广泛的系统辨识方法。由互相关法系统辨识理论, 系统输入、输出的互相关, 有:

Ryu(t)=hs(t)* Ru(t), (1)

其中:hs(t)是观测系统的冲激响应, Ru(t)是输入信号的自相关, Ryu(t)系统输入与输出信号的互相关。在复数域有:

Syu(s)=Hs(s)Su(s), (2)

其中:Syu(s)和Su(s)分别是互相关Ryu(t)和自相关Ru(t)的拉普拉斯变换, Hs(s)是观测系统自身hs(t)的拉普拉斯变换。将拉氏变量s用jω 代换, 则仪器系统的频率传递函数:

Hs(jw)=Syu(jw)Su(jw), (3)

由式(3)可获得仪器系统的频率特性。

1.1 参考信号法辨识方法

基于循环互相关法辨识仪器系统频率响应的方法[14], 是在式(3)的计算中引入了一个参考信号SS, 设置产生PRBS或逆重复M序列的寄存器位数N及固定反馈位后, 产生的序列模态是固定的; 不同的寄存器初始状态产生延时不同的时间序列, 但具有相同的频谱分布。选取时钟频率Fc, 采样率fs, 软件生成与激发波形码长相同的整数周期的PRBS或逆重复M序列时间序列作为参考信号SS。用这个参考信号SS, 分别与系统输入信号u(t)(信号产生参数与SS相同), 系统输出信号yout(t)做循环互相关(处理时将输入、输出时间序列截取为激发序列周期的整数倍), 由循环互相关时间序列的FFT变换得到互功率谱, 由式(8)和(9)恢复出系统的频率响应。

Cus(t)=cxcorr(u, SS), (4)Cys(t)=cxcorr(yout, SS), (5)PCys(ω)=FFT[Cys(t)], (6)PCus(ω)=FFT[Cus(t)], (7)H(ω)=PCys(ω)PCus(ω), (8)φ(ω)=mod{[φPCys(ω)-φPCus(ω)], π}-π, (9)

其中:cxcorr表示循环互相关运算, FFT为快速傅立叶变换, mod是模运算符; u(t)为系统输入信号时间序列(包含噪声V1(t)), yout为系统输出信号时间序列(包含噪声V2(t)), SS为软件产生的参考信号, PCys(ω )为参考信号SS与输出信号yout的互谱, PCus(ω )为参考信号SS与输入信号u(t)的互谱, φ (ω )为相位。这样处理, 即使输入、输出两端都存在工频噪声, 也有极强抗干扰能力。

1.2 循环互相关法

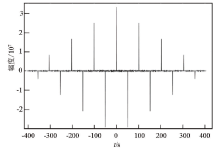
对于两个时间序列的互相关计算, 采用非循环互相关法计算时, 在序列移位过程中需要在序列头部和尾部补0, 使参与计算的2个序列长度相等, 计算结果中在相关脉冲峰两侧就会产生不需要的干扰信号, 采用多周期信号计算可以压制相关脉冲峰两侧的干扰, 但干扰仍然会存在。图1是4个周期的逆重复M序列非循环自相关计算结果, 相关峰两侧的干扰比单周期自相关减小很多, 但仍有一定幅度。且相关峰幅度随时间延迟增大而衰减。

图1 4个周期逆重复M序列非循环自相关时间序列

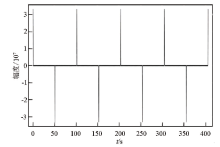
采用循环互相关法可以有效压制相关峰两侧的干扰。循环互相关法在计算时, 将每个时间序列首尾环状相连, 这样在计算中序列循环移位, 无需补0。图2是4个周期的逆重复M序列循环自相关计算结果。相关峰两侧的干扰平稳很多, 且相关峰幅度是等幅的。这个特性在多周期信号功率谱叠加中有优势。

图2 4个周期逆重复M序列循环自相关时间序列

2 仿真实验

多次仿真计算证实, 序列产生参数选择对系统特性辨识精度有直接影响, 对于基于系统辨识的地球物理实用观测系统标定, 移位时钟频率Fc、寄存器位数N以及采样率fs等参数应可选择。对于不同频带的观测仪器, 应通过实验选择产生信号参数。下面, 用仿真计算方法研究叠加周期数和采样率对辨识结果的影响,

H(s)=0.2909+1.5949s+0.3418s20.3193+3.5228s+s2。(10)

固定采样率fs为200 Hz, 逆重复M序列产生参数寄存器位数N为7, 移位寄存器时钟频率Fc为 4 Hz, 激励式(10)仿真模型。在输入和输出端均加了工频干扰, 从低频0.007 874 Hz到2.905 512 Hz, 统计了150个频点辨识得到的频率响应与理论模型频率响应幅度的均方相对误差(表1), 随采样叠加周期数增加, 均方相对误差变小, 叠加30个周期均方相对误差减小量已达到叠加50个周期均方相对误差改善的94%。

表1 均方误差随叠加周期数变化表

固定采样叠加周期数为30个周期, 在输入和输出端均加工频干扰, 从低频0.007 874 Hz到 2.905 512 Hz, 统计了150个频点辨识得到的频率响应与理论模型频率响应幅度的均方相对误差。如表2统计结果, 随采样率增加, 均方相对误差变小, 采样率为128 Hz时均方相对误差减小量已达到采样率为512 Hz时均方相对误差改善的86.4%。

表2 均方误差随采样率变化

由以上计算表明, 在有干扰条件下, 基于循环相关法相关辨识的频率响应获取方法中, 时间序列采样率和叠加周期对于辨识结果有很大影响。在低频激电法测量中, 视干扰情况, 采样率设为200 Hz, 叠加周期数30个周期为宜。

图3 基于循环相关法辨识的幅度谱

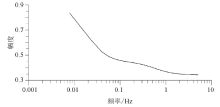
获取的频率响应频率分辨率很高。在以上所述条件下, 在10-3 Hz以下获取了1个频点, 在10-2 Hz至10-1 Hz间获取了5个频点, 在10-1~1 Hz间获取了57个频点, 在1~2 Hz间获取了48个频点, 在2~3 Hz间获取了44个频点(图3)。

对于宽频带观测仪器系统, 宜改变时钟频率, 多次激发, 以获得较宽的频率响应。

3 结论

基于系统辨识原理, 将采集的系统输入、输出信号时间序列分别与参考信号应用循环互相关法处理, 得到输出与参考信号互相关时间序列和输入与参考信号互相关时间序列, 运用快速傅立叶变换(FFT)计算互相关时间序列的互功率谱, 分别获取输出信号与参考信号的互谱的谱线峰值及对应频率, 及输入信号与参考信号的互谱的谱线峰值及对应频率, 筛选出频率相同的谱线峰值对应相除, 可恢复出待辨识仪器系统的频率响应。仿真计算结果显示, 增加信号激发周期数, 能显著提高辨识精度, 采样率也对辨识精度有影响, 对于不同频段的激发信号宜采用不同的采样率。

The authors have declared that no competing interests exist.

参考文献
[1] 滕吉文. 中国地球物理仪器的研制和产业化评述[J]. 石油物探, 2006, 45(3): 209-216. [本文引用:1]
[2] Duncan P M, Hwang A, Edwards R N, et al. The development and application of a wide-band electromagnetic sounding system using a pseudo noise source[J]. Geophysics, 1980, 45: 1276-1296. [本文引用:1]
[3] Ziolkowski A, Hobbs B, Wright D. Multitransient electromagnetic demonstration survey in France[J]. Geophysics, 2007, 72(4): 197-207. [本文引用:1]
[4] 罗维斌, 李庆春, 汤井田. 编码电磁测深[J]. 地球物理学报, 2012, 55(1): 341-349. [本文引用:1]
[5] 汤井田, 罗维斌. 基于相关辨识的逆重复m序列伪随机电磁法[J]. 地球物理学报, 2008, 51(4): 1226-1233. [本文引用:1]
[6] 淳少恒, 陈儒军, 耿明会. 伪随机m序列及其在电法勘探中的应用进展[J]. 地球物理学进展, 2014, 29(1): 439-446. [本文引用:1]
[7] 赵壁如, 赵健, 张洪魁, 等. PS100型IP到端可控源高精度大地电磁仪系统——CDMA技术首次在地电阻测量中的应用[J]. 地球物理学进展, 2006, 21(2): 675-682. [本文引用:1]
[8] 罗先中, 李达为, 彭芳苹, 等. 抗干扰编码电法仪的实现及应用. 地球物理学进展, 2014, 29(2): 944-951. [本文引用:1]
[9] 罗延钟, 陆占国, 孙国良, 等. 新一代电法勘查仪器—伪随机信号电法仪[J]. 地球物理学进展, 2015, 30(1): 411-415. [本文引用:1]
[10] 底青云, 许诚, 付长民, 等. 地面电磁探测(SEP)系统对比试验——内蒙曹四夭钼矿[J]. 地球物理学报, 2015, 58(8): 2654-2663. [本文引用:1]
[11] 何继善. 广域电磁法和伪随机信号电法[M]. 北京: 高等教育出版社, 2010. [本文引用:1]
[12] Xiao L X, Hai C Y, Xue F Z, et al. Large-scale distributed 2D/3D FDIP system based on ZigBee network and GPS[J]. Symposium on the Application of Geophysics to Engineering and Environmental Problems, 2014: 130-139. [本文引用:1]
[13] 刘立超, 丁凯来, 林君, 等. 基于伪随机系统辨识的电磁法仪器标定[J]. 仪器仪表学报, 2014, 35(8): 1721-1728. [本文引用:1]
[14] 罗维斌, 李梅. 一种获取待辨识系统频率响应函数的方法及装置. 中国专利CN 104794313 A, 2015. [本文引用:2]
[15] Tangirala A K. Principles of system identification theory and practice[M]. Crc Press, 2014. [本文引用:1]
[16] Kaufman A A, Alekseev, Oristaglio ML. Principles of electromagnetic methods in surface geophysics[M], Elsevier, 2014. [本文引用:1]
[17] Maurizio D P E. Data Acquisition Systems: From Fundamentals to Applied Design[M]. New York: Springer Science+Business Media, 2015. [本文引用:1]
[18] Martin H. MATLAB recipes for earth sciences(Fourth Edition)[M]. New York: Springer Science+Business Media, 2015. [本文引用:1]
[19] Tomi R, Tomi H, Matti V, et al. , Circular correlation based identification of switching power converterwith uncertainty analysis using fuzzy density approach[J]. Simulation Modelling Practice and Theory, 2009, 17(3): 1043-1058. [本文引用:1]
[20] Luo W B. Study on Pseudorand om Marine Controlled-Source Electromagnetic sounding withmulti-offsets[D]. Changsha: Central South University, 2007. [本文引用:1]
[21] Ziolkowski A, Hobbs B, Dawes G, et al. True amplitude transient electromagnetic system response measurement[P]. US, 7957904_B2, 2006-11-02. [本文引用:1]
[22] Ziolkowski A, Optimization of MTEM parameters[P]. US, 20090230970_A1, 2009-09-17. [本文引用:1]
[23] 张宇, 王兰炜, 张兴国, 等. 相关检测技术在低频交流地电阻率观测中的应用[J]. 地球物理学进展, 2014, 29(4): 1973-1979. [本文引用:1]
[24] 夏正武, 刘国强, 李士强, 等. 一种自动同步的可控源频率域电磁探测系统[J]. 地球物理学进展, 2014, 29(2): 952-957. [本文引用:1]