波动方程模拟PML吸收影响因素分析

引用本文

刘瑞合, 印兴耀, 浦义涛. 波动方程模拟PML吸收影响因素分析[J]. 物探与化探, 2016,40(4): 757-762.
LIU Rui-He, YIN Xing-Yao, PU Yi-Tao. Analyzing PML absorbing impact factors with wave equation simulation[J]. Geophysical and Geochemical Exploration, 2016,40(4): 757-762.
Doi:10.11720/wtyht.2016.4.19 复制到剪切板

Permissions

《物探与化探》编辑部所有

波动方程模拟PML吸收影响因素分析

刘瑞合¹, 印兴耀¹, 浦义涛²

1.中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

2.中国石油东方地球物理公司塔里木物探处,新疆库尔勒 841001

作者简介: 刘瑞合(1977-),男,高级工程师,中国石油大学(华东)在读博士,主要从事地震资料处理方法研究与应用工作。

收稿日期: 2015-09-11

基金: 国家重点基础研究发展计划(“973”)(2013CB228604); 山东省自然基金项目(ZR2014DM009)联合资助

摘要

地震数值模拟中,完全匹配层(PML)边界能有效地吸收衰减地震波,得到无边界反射干扰的波场快照和地震记录。在前人研究的基础上,进一步分析了分裂完全匹配层(SPML)的衰减机制,通过波动方程模拟,分析了震源主频、空间网格间距、介质速度等参数对SPML边界吸收衰减特征的影响。得到了不同条件下,PML边界对地震波的吸收效果。通过分析对比,得出了震源主频对PML吸收效果无直接影响,空间网格间距与PML吸收效果成反比,高速层PML吸收效果缓慢等结论。并通过Marmousi2模型测算,对结论进行了验证。最后给出了复杂模型、不同尺度数值模拟中SPML参数的选取方法,为地震数值模拟中SPML边界参数的定量选取奠定了基础。

关键词: 地震数值模拟; 波动方程; 完全匹配层; 吸收衰减特征; 小尺度

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)04-0757-06 doi: 10.11720/wtyht.2016.4.19

Analyzing PML absorbing impact factors with wave equation simulation

LIU Rui-He¹, YIN Xing-Yao¹, PU Yi-Tao²

1. School of Geoscience,China University of Petroleum,Qingdao 266580,China

2.Bureau of Geophysical Prospecting INC.,China National Petroleum Corporation,Korla 841001,China

Abstract

In seismic numerical simulation, the perfectly matched layer (PML) boundary can attenuate the seismic wave effectively,and the snapshots and record have no boundary reflection interferes.The authors further analyzed the attenuation mechanism of split perfectly matched layer (SPML).By wave equation simulation, the authors analyzed the problem as to how the parameters affect absorption and attenuation characteristics of SPML boundary,such as source dominant frequency,spatial grid spacing and medium speed.As a result,the authors obtained the results of PML attenuation based on different conditions.Through analyzing and comparing the results,the conclusions have been reached that source dominant frequency has no direct influence on PML attenuation,spatial grid spacing is in inverse proportion to the PML attenuation,and high-speed medium slows down PML attenuation effect.By Marmousi2 test,the authors confirmed the validity of the conclusions.The selection method of SPML parameter in complex model or different scales of numerical simulation was given,which lays a foundation for quantitative selection of SPML boundary parameters in numerical simulation.

Keyword: seismic numerical simulation; wave equation; PML; absorption and attenuation characteristics; small scale

Show Figures

地震数值模拟是观察地震波在复杂介质传播规律和特征的有效手段。由于存储和计算的限制, 只能在有限空间模型中进行计算, 这就不可避免的产生边界反射。为了消除边界反射, 提高地震模拟质量, 边界处理就显得尤为重要。目前, 应用较为广泛的边界条件主要有衰减边界条件和透射边界条件。衰减边界条件主要有Cerjan等^[1]提出的海绵边界和Berenger^[2]提出的完全匹配层(PML)边界, 透射边界主要为Clayton等^[3]提出的傍轴近似边界。海绵边界通过衰减层来吸收地震波, 需要足够厚的吸收层才能获得满意的效果, 增加较多的计算量。傍轴近似边界只能对特定入射角和频率的地震波有效, 对面波吸收不理想。PML边界可以完全吸收来自各个方向、各个频率的波, 而不产生任何边界反射。

在有限差分双程波数值模拟中常用衰减边界条件, 其中PML完全匹配层边界使用最多 $\begin{matrix} ^{[47]} \end{matrix}$ 。PML边界首先由Berenger提出, Hastings等^[8]推导了一阶速度— 应力弹性波方程的PML边界, Collino等^[9]推导了分裂完全匹配层(SPML)边界的衰减机制, 将其运用于各向异性非均匀介质数值模拟中。并且, PML边界条件在黏弹性介质^[10]和双相介质^[11]的数值模拟中也得到成功运用。PML边界分为分裂(SPML)和不分裂(NPML、CPML)两种形式, 由于SPML边界相对简单、容易实现, 目前的数值模拟中多数还是使用SPML边界^[12] 。

虽然前人已在不同介质中成功应用了SPML边界 $\begin{matrix} ^{[810]} \end{matrix}$ , 但是尚未有深入分析SPML边界的研究。笔者在前人研究的基础上(Collino^[9], 2001), 进一步分析了SPML边界的衰减机制, 地震数值模拟中震源主频、空间网格间距、介质速度等因素对SPML边界条件吸收衰减效果的影响。得出高速层SPML边界衰减较慢, 小尺度数值模拟中边界网格成倍增加的结论^[13] , 理清了SPML边界中, 地震波波长、边界厚度与吸收效果的关系。对不同介质、不同尺度地震数值模拟中SPML边界的参数设置起到了指导作用, 为地震数值模拟中SPML边界参数的定量选取奠定了基础。

1 方法原理

计算区域的地震波垂直入射到SPML边界时、经过衰减的子波与无边界时、未衰减的子波振幅比为^{[9, 14]}:

$\begin{matrix} \frac{‖ u^{*} (x, t) ‖}{‖ u (x, t) ‖} = \exp [- \frac{k_{x}}{ω} \int_{0}^{x} d_{x} (s) ds], (1) \end{matrix}$

其中:u^*(x, t)表示完全匹配层中的子波, u(x, t)表示无边界的子波, d_x(x)是衰减项; k_x是波数, ω 是角频率。由式(1)可知, 在SPML边界, 波场值随距离的传播呈指数衰减。

衰减项主要有三角函数形式^[15] 和指数形式 $\begin{matrix} ^{[2, 4, 5, 812, 14]} \end{matrix}$ , 由于指数形式最为常见, 文中仅讨论指数形式的衰减项。

$\begin{matrix} \begin{matrix} d_{x} (x) = d_{\max} {(\frac{x}{H})}^{n}, (2) \\ d_{\max} = - \frac{(n + 1) c_{\max}}{2 H} \ln (R) 。 (3) \end{matrix} \end{matrix}$

其中:x为到PML层内边界的距离, H为PML层厚, d_max为最大衰减值^[12] ; R为理论反射系数, 取10^-6; c_max为介质速度最大值。实验表明, 当n=4时, 具有较好的效果和稳定性^[8] 。基于Hastings的研究成果^[8], 进一步分析了震源主频、空间网格间距、介质速度等参数对SPML边界吸收衰减特征的影响。

将式(2)代入式(1)得:

$\begin{matrix} \frac{‖ u^{*} (x, t) ‖}{‖ u (x, t) ‖} = \exp [- \frac{k_{x}}{ω} \int_{0}^{x} d_{\max} {(\frac{s}{H})}^{n} ds] 。 (4) \end{matrix}$

又由于波数k_x=ω /c, c是介质速度。代入式(3)后, 式(4)可进一步简化为:

$\begin{matrix} \frac{‖ u^{*} (x, t) ‖}{‖ u (x, t) ‖} = \exp [\frac{\ln (R)}{2} \frac{c_{\max}}{c} {(\frac{x}{H})}^{n + 1}] 。 (5) \end{matrix}$

式(5)即为SPML边界的衰减公式。当模型为均匀介质时, c_max=c, SPML衰减效果只与SPML层厚H, 到SPML层内边界的距离x和多项式的阶数n有关; 当模型为非均匀介质时, c_max≥ c, SPML衰减效果还与介质速度c有关。

2 影响因素分析

采用时间二阶、空间十阶差分精度的声波方程进行模拟。震源位于模型中央, 检波点布置在SPML边界周围。由于有限差分的离散性, 介质属性在计算区域与SPML交界面会产生突变。当地震波从计算区域内向SPML吸收区域传播时, 会在两者的分界面处产生数值反射波。所以, 不同模型下, 合理的设置最大衰减项d_max, 减小数值反射波, 从而提高SPML边界吸收衰减效果。笔者通过提取每道地震记录的峰值, 来反应SPML层内的吸收衰减特征, 并定义数值反射波强度的表达式为:反射强度=反射波/入射波。

2.1 SPML层数的选取

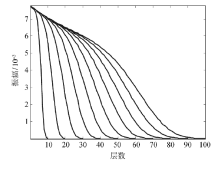
采用一个1 000 m× 1 000 m的均匀介质模型, 速度为3 000 m/s。模型的空间网格间距Δ x=Δ z=10 m, 采样间隔Δ t=1 ms, 震源为主频20 Hz的Ricker子波。分析了SPML边界分别设置为10~100层时, SPML边界的吸收衰减特性(图1)。

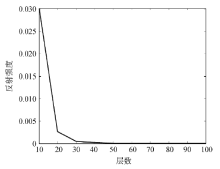
	Figure Option View Download New Window
	图1 不同层数的SPML吸收衰减特征

通过图1可以发现, 不同层数的SPML边界都能对子波进行较好的衰减; SPML层数越大, 衰减越平缓。由式(3)可知, 最大衰减项d_max与SPML厚度成反比。当SPML层数减小时, 最大衰减项d_max增大, 导致数值反射波强度陡增, 从而影响SPML吸收衰减效果。图2给出了不同SPML层数的数值反射波强度, 其中可以看出, 20层和30层处为明显的拐点。这是由于PML边界的存在导致地震波传到边界时会产生反射波, 而反射波强度的大小取决最大衰减项d_max。在如今的地震模拟中, 一般采用10层左右的PML边界即可取得比较不错的吸收效果 $\begin{matrix} ^{[911]} \end{matrix}$ , 但是会有比较强的数值反射波(图2)。综合PML边界条件的实用性以及数值计算的经济性考虑, 为了达到较好的吸收衰减特征, 同时减小数值反射波, SPML层选取20~30层较为理想。

	Figure Option View Download New Window
	图2 不同层数的数值反射波强度

2.2 震源主频的影响

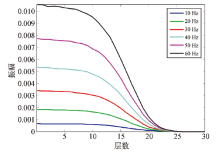
在式(1)中, SPML吸收衰减特征与频率有关, 而式(5)消除了频率项的影响。为了验证频率对SPML吸收衰减特征的影响, 在2.1小节的模型基础上, 震源分别设置为10~60 Hz的Ricker子波。同时为避免频散, 空间网格间距均取5 m, SPML层数设为30层。

图3中不同主频子波的最大振幅均为1, 子波能量随着主频增加而增加。所以传播相同距离后60 Hz子波能量最高, 衰减的最剧烈; 10 Hz子波能量最低, 衰减最缓慢。但在25层之后, 能量基本都衰减为零。说明不同主频子波, 在相同空间网格间距情况下, SPML吸收衰减特征基本一致, 震源主频并没有影响。对于井间地震和声波测井等高频波动方程正演模拟, 随着频率的增大, 为了避免频散, 空间网格间距变小。但在相同空间网格间距条件下, 结论依然成立。

	Figure Option View Download New Window
	图3 不同震源主频的SPML吸收衰减特征

2.3 介质速度的影响

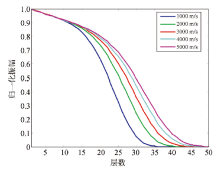
采用五个速度从1 000~5 000 m/s变化的均匀介质模型, 由于低速层的存在, 空间网格间距设为5 m, 由于空间网格变小, SPML层数设为50层, 模型大小1 000 m× 1 000 m, 震源为主频20 Hz的Ricker子波。图4为振幅归一化后, 不同速度的SPML吸收衰减特征。

通过图4可以发现, SPML吸收衰减特征与层速成反比, 速度越大, SPML衰减越缓慢。为了得到无边界反射干扰的波场快照和地震记录, 需要考虑高速层的SPML吸收衰减特征。

	Figure Option View Download New Window
	图4 不同速度的SPML吸收衰减特征

由此可见, SPML边界对不同波长子波的吸收衰减特征的差异主要体现在速度的区别, 而与子波主频无关。

2.4 空间网格间距的影响

地震勘探所面临的地质条件愈加复杂, 介质速度变化剧烈。为了保证计算的精度和稳定性, 更好地表征地质体的地震反射特征。针对不同地质条件, 采用不同空间网格间距进行数值模拟是有效途径。

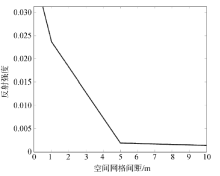
通过式(3)可知, 当SPML层数固定、空间网格间距变化时, 最大衰减项d_max与空间网格间距成反比。图5给出了30层SPML, 空间网格间距分别为0.5、1、5和10 m的数值反射波强度。

	Figure Option View Download New Window
	图5 不同空间网格间距的数值反射波强度

当空间网格间距减小时, 最大衰减项d_max增大, 从而导致数值反射波加强, 干扰地震记录。因此, 在不同空间网格间距的数值模拟中, SPML的最大衰减项d_max均应取较小的值, 才能有效控制数值反射波的强度, 获得无边界反射干扰的地震记录。

对于不同空间网格间距的SPML, 我们均采用空间网格间距为10 m时所对应的最大衰减项d_max。此时, 式(5)变为

$\begin{matrix} \frac{‖ u^{*} (x, t) ‖}{‖ u (x, t) ‖} = \exp [- \frac{H}{c} \frac{d_{\max}}{n + 1} {(\frac{x}{H})}^{n + 1}] 。 (6) \end{matrix}$

可见, 当最大衰减项d_max固定时, 相同SPML层数, 空间网格间距越小, 衰减效果越弱。

在1 000 m× 1 000 m的模型中, 分别以0.5、1、5和10 m四种空间网格间距进行数值模拟。介质速度为3 000 m/s, 震源为主频20 Hz的Ricker子波, SPML边界分别设置为600、300、60和30层。

通过图6可以看出, 为达到相同衰减效果, 不同空间网格间距数值模拟所需要的SPML厚度相同(图6a), 空间网格间距越小, 需要的SPML层数就越多(图6b)。这也就解释了在小尺度数值模拟中, SPML边界所需层数成倍增加的原因。

	Figure Option View Download New Window
	图6 不同空间网格间距的SPML吸收衰减特征

3 数值算例

3.1 相同层数SPML边界

采用Marmousi2模型验证所得结论的正确性, 模型长17 000 m、深3 500 m, 具有多个复杂构造和圈闭。分别以1.25、5和10 m空间网格间距进行数值模拟, 震源为主频20 Hz的Ricker子波, SPML边界均取50层, 得到5 500 ms的地震记录。

对比图7b、图7c和图7d可以看出, 相同层数SPML, 随着网格间距不断减小, 边界反射愈加严重 (图7d箭头指示处)。由于尺度越小, 模型越精细, 所以地震记录内容越丰富。图7c中, 右侧边界反射明显强于左侧, 这是由于模型右边存在高速层所致, 导致SPML边界的吸收衰减效果减弱, 边界反射增强。并且, 由于模型右侧高速层相对于左侧高速层埋藏较浅, 5 500 ms的地震记录只记录到模型右侧高速层的反射波, 导致记录右侧反射波旅行时小于左侧。

	Figure Option View Download New Window
	图7 Marmousi2模型地震记录

3.2 相同厚度SPML边界

其他参数不变, SPML边界分别取320层、80层和40层, 边界厚度均为400 m。采用2.4中的方法, 得到归一化振幅与层数和层厚的关系曲线。由图8可见, 2.4所得结论在复杂地质条件下依然成立, 验证了结论的正确性。

	Figure Option View Download New Window
	图8 Marmousi2模型中SPML边界的吸收衰减特征

4 结论

在分裂完全匹配层(SPML)边界衰减机制的基础上, 通过波动方程模拟, 进一步分析了影响SPML吸收衰减特征的因素, 并通过Marmousi2模型分析验证, 得到以下结论:为了得到无边界反射干扰的波场快照和地震记录, 在空间网格间距为10 m的情况下, SPML层设为20~30层较为理想; 在相同空间网格间距条件下, 震源主频对SPML吸收衰减特征并无影响; 在高速层中, SPML衰减较慢, 需要考虑高速层对SPML吸收衰减特征的影响; 不同波长子波的SPML吸收衰减特征差异主要体现在速度的区别, 与子波主频无关; 为达到相同衰减效果, 不同空间网格间距数值模拟需要相同厚度的SPML边界, SPML层数与空间网格间距成反比。

由此可见, 对复杂模型在不同尺度下的数值模拟, 需要选取适当的SPML边界参数, 才能获得较好的吸收衰减效果, 得到无边界反射干扰的波场快照和地震记录。文中具体分析了影响SPML边界的吸收衰减因素, 明确了对SPML边界衰减机制的认识。给出了复杂模型、不同尺度数值模拟中SPML参数的选取方法, 为地震数值模拟中SPML边界参数的定量选取奠定了基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708. [本文引用:1]
[2]	Berenger J. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. [本文引用:1]
[3]	Clayton R, Engquist B. Absorbing boundary conditions for wave-equation migration[J]. Geophysics, 1980, 45(5): 895-904. [本文引用:1]
[4]	郭念民, 吴国忱. 基于PML边界的变网格高阶有限差分声波方程逆时偏移[J]. 石油地球物理勘探, 2012, 47(2): 256-265. [本文引用:1]
[5]	孙林洁, 印兴耀. 基于PML边界条件的高倍可变网格有限差分数值模拟方法[J]. 地球物理学报, 2011, 54(6): 1614-1623. [本文引用:1]
[6]	张岩, 吴国忱. TTI介质qP波逆时偏移中伪横波噪声压制方法[J]. 地球物理学报, 2013, 56(6): 2065-2076. [本文引用:1]
[7]	印兴耀, 浦义涛, 梁锴, 等. VTI介质准P波旋转交错有限差分数值模拟[J]. CT理论与应用研究, 2014, 23(5): 771-783. [本文引用:1]
[8]	Hastings F D, Schneider J B, Broschat S L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061-3069. [本文引用:3]
[9]	Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. [本文引用:3]
[10]	Liu Q, Tao J. The perfectly matched layer for acoustic waves in absorptive media[J]. The Journal of the Acoustical Society of America, 1997, 102(4): 2072-2082. [本文引用:1]
[11]	Zeng Y, He J, Liu Q. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media[J]. Geophysics, 2001, 66(4): 1258-1266. [本文引用:1]
[12]	张鲁新, 符力耘, 裴正林. 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用[J]. 地球物理学报, 2010, 53(10): 2470-2483. [本文引用:2]
[13]	Pu Y T, Yin X Y, Cao D. The PML boundary of small-scale seismic modeling[J]. SEG Technical Program Expand ed Abstracts, 2014: 3493-3497. [本文引用:1]
[14]	王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003, 38(1): 31-34. [本文引用:1]
[15]	张剑锋, 徐义. 地震波数值模拟的非规则网格PML吸收边界[J]. 地球物理学报, 2008, 51(5): 1520-1526. [本文引用:1]

1985

0.0

... 衰减边界条件主要有Cerjan等^[1]提出的海绵边界和Berenger^[2]提出的完全匹配层(PML)边界,透射边界主要为Clayton等^[3]提出的傍轴近似边界 ...

1994

0.0

... 衰减边界条件主要有Cerjan等^[1]提出的海绵边界和Berenger^[2]提出的完全匹配层(PML)边界,透射边界主要为Clayton等^[3]提出的傍轴近似边界 ...

1980

0.0

... 衰减边界条件主要有Cerjan等^[1]提出的海绵边界和Berenger^[2]提出的完全匹配层(PML)边界,透射边界主要为Clayton等^[3]提出的傍轴近似边界 ...

2012

0.0

郭念民, 吴国忱. 基于PML边界的变网格高阶有限差分声波方程逆时偏移[J]. 石油地球物理勘探, 2012, 47(2): 256-265.

叠前逆时深度偏移采用全声波方程求解，不受介质横向速度变化和高陡倾角的影响，具有成像精度高、相位准确、实现回转波成像等优点。逆时偏移利用双程波动方程构造波场延拓算子，正向延拓时间域震源点波场，逆时反向外推时间域检波点波场，然后利用互相关成像条件实现成像，因此正演模拟技术是其成功与否的关键。当浅层为海水或者低速层时，常规的有限差分方法必须采用小网格才能有效压制频散，得到高质量的波场记录，从而保证成像精度。但是若对整个区域都用小网格和小的时间采样间隔进行波场计算，势必造成计算量的增加。本文给出了声波方程变网格算法的差分格式，推导了基于PML边界条件的变网格高阶有限差分方程，将可变网格和可变时间步长算法应用于逆时偏移的波场外推，既保证了波场外推计算的精度和最终逆时偏移的成像效果，同时又提高了计算效率，并通过数值算例试算和逆时偏移成像的应用，说明了该方法的有效性和可行性。

2011

0.0

孙林洁, 印兴耀. 基于PML边界条件的高倍可变网格有限差分数值模拟方法[J]. 地球物理学报, 2011, 54(6): 1614-1623.

Heterogeneous media is a kind of multi-scale media. The scale of the fracture reservoir could reach up to millimeter. Simulating a fractured carbonate model with finite-difference method is calling for the same scale of sample steps. A finite-difference method with high power of grid steps variation is presented here. Spatial and temporal sampling steps can be optimized according to material properties and model geometry. The ratio of grid steps could reach up to hundreds or more. We improve the method of numerical grid division in order to add more flexibility and efficiency to finite-difference method with grid variation. The numerical results support that the method can describe heterogeneous media in scale of millimeter accurately with efficiency, and the property made the method suitable for modeling cavity or fractured carbonate reservoirs.

非均匀介质一般为多尺度介质,对非均匀介质进行正演模拟需要多尺度的网格剖分.碳酸盐岩缝洞介质的尺度一般为厘米级甚至毫米级.使用有限差分方法对其进行精细模拟需要差分步长达到缝洞介质的尺度.为了提高有限差分数值模拟方法的精度和效率,使之可以应用于非均匀介质的正演模拟,本文推导了基于PML边界的空间和时间步长同时变化的高倍数可变网格差分格式,步长变化倍数可以达到百倍以上.并且在一般意义的变网格算法的基础上,改进了变网格算法的网格剖分方式,进一步减小了精细尺度模型数值模拟的内存消耗.数值试验表明,该方法可以精细描述毫米尺度的地质体,提高有限差分方法模拟精度,同时也节约了内存,提高了模拟效率.

2013

0.0

张岩, 吴国忱. TTI介质qP波逆时偏移中伪横波噪声压制方法[J]. 地球物理学报, 2013, 56(6): 2065-2076.

In the process of imaging subsurface complex structure media, in particular with salt flank and the area bellow it, compared to the method of traditional isotropic reverse-time migration and VTI reverse-time migration, TTI reverse-time migration can produce the best image, not only the continiuity of reflection is much better, but also the energy can be focused more intensely. The traditional anisotropic full elastic wave reverse-time migration clearly is more computer resources demanding and inefficient. Because the information of qP-wave is still playing the leading role in seismic exploration at present, the methods of choosing qP-wave equations in TTI reverse-time migration become pretty important. For improving the calculating efficient, the anisotropic elasto-dynamic equations of motions are often simplified to acoustic equations which only allow qP-wave propagate by seting the velocity of SV-wave equal to zero along the symmetry axis orientation. However, it can bring a low-speed and low-amplitude qSV-artifacts which will destroy the results of reverse-time migration greatly. Firstly, We build the PML controlling equations of qP wave equations. After that, combined with the auxiliary wavefield, in this paper we introduce a cost-effective method which suppresses pseudo SV-wave artifacts perfectly. Numerical examples are included to show the validity of the algorithm.

在对地下复杂构造介质,特别是盐丘侧翼及岩下区域进行成像时,相对于传统的各向同性逆时偏移和VTI逆时偏移,具有倾斜对称轴的TTI逆时偏移成像效果最优.不仅反射同相轴更加的连续,而且能量得到了更好的聚焦.传统的各向异性介质全弹性波RTM的计算量大且计算效率低.由于目前仍以纵波勘探为主,因此TTI逆时偏移qP波波动方程的选取显得尤为重要.为了提高计算效率,采用将沿着对称轴方向的横波速度设为零的方法,简化得到qP波波动方程.然而,这样会引入一种严重影响成像效果的低速度、低振幅的qSV波人为干扰.本文建立了qP波方程的完全匹配层控制方程,而后借助于辅助波场采用一种高效的压制伪横波噪声传播的方法,通过模型测试验证了该方法的有效性.

2014

0.0

印兴耀, 浦义涛, 梁锴, 等. VTI介质准P波旋转交错有限差分数值模拟[J]. CT理论与应用研究, 2014, 23(5): 771-783.

本文采用旋转交错网格差分格式对VTI(垂直对称轴的横向各向同性)介质准P波一阶应力-速度方程进行数值模拟。并在PML边界条件和稳定性条件下得出Marmousi等复杂模型的高精度波场快照和地震记录,分析了各向异性对地震波的影响。数值结果表明:旋转交错网格有限差分能获得高精度的地震模拟数据,PML边界有较好的吸收效果。

1996

0.0

... PML边界首先由Berenger提出,Hastings等^[8]推导了一阶速度#cod#x02014 ...

... 实验表明,当n=4时,具有较好的效果和稳定性^[8] ...

... 基于Hastings的研究成果^[8],进一步分析了震源主频、空间网格间距、介质速度等参数对SPML边界吸收衰减特征的影响 ...

2001

0.0

... 应力弹性波方程的PML边界,Collino等^[9]推导了分裂完全匹配层(SPML)边界的衰减机制,将其运用于各向异性非均匀介质数值模拟中 ...

... 笔者在前人研究的基础上(Collino^[9], 2001),进一步分析了SPML边界的衰减机制,地震数值模拟中震源主频、空间网格间距、介质速度等因素对SPML边界条件吸收衰减效果的影响 ...

... 1 方法原理计算区域的地震波垂直入射到SPML边界时、经过衰减的子波与无边界时、未衰减的子波振幅比为^[9,14]: ...

1997

0.0

... 并且,PML边界条件在黏弹性介质^[10]和双相介质^[11]的数值模拟中也得到成功运用 ...

2001

0.0

... 并且,PML边界条件在黏弹性介质^[10]和双相介质^[11]的数值模拟中也得到成功运用 ...

2010

0.0

张鲁新, 符力耘, 裴正林. 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用[J]. 地球物理学报, 2010, 53(10): 2470-2483.

Perfectly matched layer (PML) absorbing boundary has been widely used in seismic simulation. At grazing incidence and low frequency, the classical split PML (SPML) method and the traditional nonsplit PML (NPML) method suffer from large spurious reflections. An unsplit convolutional PML (CPML) not only fixes the disadvantages of conventional PML, but also needs less memory, computes efficiently and is easy to program. In this paper, this CPML absorbing boundary is imported to the rotated grid finite-difference method, in velocity-stress formulation, of poroelastic media. The numerical analysis of parameters in the PML absorbing boundary gives a set of optimum parameters. Numerical test shows that the CPML absorbing boundary gives a better result than the conventional PML absorbing boundary.

完全匹配层吸收边界在地震波模拟中已广泛使用,但常用的场分裂格式完全匹配层吸收边界(SPML)和传统的不分裂完全匹配层吸收边界(NPML)对极低频入射波或大角度入射波的边界吸收效果不好.一种无需分裂和显式卷积计算的完全匹配层吸收边界(CPML)不仅能够解决常规PML吸收边界的不足,而且具有存储量小、计算效率高、易于编程实现的特点.本文将这种完全匹配层(CPML)吸收边界引入到孔隙弹性介质速度-应力格式的旋转交错网格有限差分算法中,对完全匹配层吸收边界参数进行数值分析,得到一组优化的参数.孔隙弹性介质数值模拟结果表明这种不分裂卷积完全匹配层的吸收效果优于常规完全匹配层.

... PML边界分为分裂(SPML)和不分裂(NPML、CPML)两种形式,由于SPML边界相对简单、容易实现,目前的数值模拟中多数还是使用SPML边界^[12] ...

... 其中:x为到PML层内边界的距离,H为PML层厚,d_max为最大衰减值^[12] ...

2014

0.0

... 得出高速层SPML边界衰减较慢,小尺度数值模拟中边界网格成倍增加的结论^[13] ,理清了SPML边界中,地震波波长、边界厚度与吸收效果的关系 ...

2003

0.0

王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003, 38(1): 31-34.

Aimed at acoustic wave equation, the papergave absorbing boundary condition by using perfectly matched layer.The basic ideal of the methodis that absorbing layer is added on the boundary ofinteresting region, no reflection is produced whenwave propagates from boundary of studied regionto absorbing layer and wave attenuates exponendally with propagation distance.The paper alsogave the basic principle of perfectly matched layer,introduced the control equation of perfectlymatched layer for acoustic wave equation,and finally showed several satisfactory numerical modeling results.

本文针对声波方程,给出了完全匹配层吸收边界方法。其基本思想是在所研究区域的边界上引入吸收层,波由研究区域边界传到吸收层时不产生任何反射,在吸收层内按传播距离的指数规律衰减,不产生反射,从而达到吸收边界的效果。文中给出了完全匹配层方法的基本原理,导出了声波方程完全匹配层的控制方程,并给出了令人满意的数值模拟结果。

... 1 方法原理计算区域的地震波垂直入射到SPML边界时、经过衰减的子波与无边界时、未衰减的子波振幅比为^[9,14]: ...

2008

0.0

张剑锋, 徐义. 地震波数值模拟的非规则网格PML吸收边界[J]. 地球物理学报, 2008, 51(5): 1520-1526.

The perfectly matched layer (PML) absorbing boundary condition is incorporated into the acoustic grid method, thus resulting in an irregular-grid PML method. The proposed scheme is developed using the local coordinate system based PML splitting equations and integral approaches of the PML equations under a discretization of triangular grid cells. The irregular-grid PML method allows the artificial boundaries to be constructed with arbitrary geometries only if the interested zones are enclosed. We can take a semi-circle rather than a rectangle as the artificial boundary in simulating the 2-D half-space using the proposed scheme. This results in an over 20% reduction of the nodes in the numerical discretization. By using a smoothed artificial boundary, the irregular-grid PML method can also avoid the special treatments for the corners, which lead to complex computer implementations in the conventional PML method. Owing to that the local geometrical coefficients are computed and stored in a table in advance, no extra computational costs arise when we use the irregular-grid PML method rather than the conventional PML method. The 2-D acoustic cases are considered here.

以格子法为基础，以声波方程为例研究非规则网格PML(Perfectly Matched Layer)方法.本方法的核心是建立局部坐标系下的分裂方程和基于积分近似的微分方程弱形式.该非规则网格模拟方法允许在计算域内设置任意形状的人工边界.对于二维半空间问题，与采用矩形人工边界相比，采用半圆形人工边界可减少计算量20%以上.采用光滑的曲边界，不仅可减少计算区域，还可避免常规的PML吸收边界在吸收带角点区域的特殊处理.本方法事先计算和存储边界单元的局部几何参数，在计算的每一时间步查表调用这些参数，与常规的直边界PML方法相比，不增加任何计算量.

... 衰减项主要有三角函数形式^[15] 和指数形式 [2,4,5,812,14],由于指数形式最为常见,文中仅讨论指数形式的衰减项 ...