基于复值曲波变换的地震数据重建方法

引用本文

徐卫, 张华, 张落毅. 基于复值曲波变换的地震数据重建方法[J]. 物探与化探, 2016,40(4): 750-756.
XU Wei, ZHANG Hua, ZHANG Luo-Yi. A study of seismic data reconstruction based on complex-valued curvelet transform[J]. Geophysical and Geochemical Exploration, 2016,40(4): 750-756.
Doi:10.11720/wtyht.2016.4.18 复制到剪切板

Permissions

《物探与化探》编辑部所有

基于复值曲波变换的地震数据重建方法

徐卫^1,², 张华³, 张落毅³

1.中南大学地球科学与信息物理学院,湖南长沙 410083

2.山西省煤炭地质物探测绘院,山西晋中 030600

3.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌 344000

作者简介: 徐卫(1976-),男,硕士研究生,主要从事地球物理勘探工作。

收稿日期: 2015-07-22

基金: 国家青年科学基金项目(41304097)和江西省自然科学基金项目(20151BAB203044)联合资助

摘要

传统的地震数据采样必须遵循奈奎斯特采样定理,而野外数据采样可能由于地震道缺失或者勘探成本限制,不一定满足采样定理的要求,因此需要进行叠前数据重建,以满足后续处理的要求。为此,笔者提出一种基于复值曲波变换和凸集投影算法(POCS)的地震数据重建方法。首先引入凸集投影算法和能够刻画地震数据局部化特征的复值曲波变换,在重建过程中针对传统阈值参数收敛速度较慢的缺点,提出了指数平方根衰减规律的阈值参数,并采用硬阈值算子对二维地震数据进行重建,从而降低了迭代次数,提高了重建精度。通过理论数据的研究表明,该方法重建效果显著,最后将该技术应用于实际地震勘探资料,获得较好的应用效果。

关键词: 复值曲波变换; 阈值; 数据重建; 凸集投影; 随机采样

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)04-0750-07 doi: 10.11720/wtyht.2016.4.18

A study of seismic data reconstruction based on complex-valued curvelet transform

XU Wei^1,², ZHANG Hua³, ZHANG Luo-Yi³

1.School of Geosciences and Info-physics,Central South University,Changsha 410083,China

2.Geophysical Prospecting,Surveying and Mapping Institute,Shanxi Coal Geological Exploration,Jinzhong 030600,China

3.Fundamental Science on Radioactive Geology and Exploration Technology Laboratory,East China Institute of Technology,Nanchang 344000,China

Abstract

Traditional seismic data sampling must follow the Nyquist sampling theorem;nevertheless,the field data acquisition can't meet the sampling theorem due to missing traces or exploration cost limits,so we need to reconstruct prestack data to meet the requirements for subsequent processing.A seismic data reconstruction method based on the Projections Onto Convex Sets (POCS) algorithm and a complex-valued curvelet transform (CCT) has been introduced in the paper.Firstly,the Projections Onto Convex Sets (POCS) and complex-valued curvelet transform to characterize the local features of seismic data have been introduced.To tackle the disadvantage of slow convergence in traditional threshold parameter during the reconstruction process,the authors also propose an exponential square root decreased threshold and process 2-D seismic data reconstruction with the hard thresholding,which can reduce iterations and improve reconstruction efficiency.The case study of synthetic seismic data shows that the effect of this method is fairly good.The authors applied this technology in real seismic data and obtained a good result.

Keyword: complex-valued curvelet transform; threshold parameter; data reconstruction; Projection onto Convex Sets(POCS); random sampling

Show Figures

在野外数据采集过程中, 由于采集设备和经济成本的限制, 地震数据沿空间方向上通常进行不规则采样, 从而导致采集到的地震数据不规则、不完整, 出现空间假频 $\begin{matrix} ^{[14]} \end{matrix}$ , 这种稀疏分布的地震数据难以满足后续处理(例如速度分析、自由表面多次波消除、偏移归位等)的要求, 在这种情况下, 需要发展较好的叠前数据插值方法, 重建出缺失的地震道。另一方面, 如果有适当的重建方法, 可以降低野外采集成本, 提高施工效率 $\begin{matrix} ^{[58]} \end{matrix}$ 。

常用的数据重建方法主要有基于某种数学变换的插值技术, 例如Radon变换 $\begin{matrix} ^{[912]} \end{matrix}$ 、傅里叶变换^{[2, 13]}、Curvelet变换 $\begin{matrix} ^{[1419]} \end{matrix}$ 等。而数据重建方法也较多, 凸集投影算法由于参数设置简单且效果显著而被广泛应用 $\begin{matrix} ^{[2021]} \end{matrix}$ , 其主要思想就是在每次迭代过程中, 采用二维傅立叶变换将时间— 空间域数据变换到频率— 波数域, 然后设置一个阈值保留较大振幅的有用信号, 再对保留后的有用信号采用二维傅立叶反变换, 最后将原始不需要重建的地震道置换到二维傅立叶反变换后的数据中去, 通过多次迭代, 将缺失地震道重建出来。然而在以往文章中, 采用的是傅立叶变换作为稀疏基, 并不能很好地重建出数据的局部特征, 效果有限。刘国昌等^[22]采用曲波变换作为稀疏基, 相比于二维傅立叶变换, 该方法更能够重建非线性同相轴, 更加适合具有各向异性特征的地震波场, 但他没有对阈值参数选择作进一步研究。为此, 在前人研究的基础上, 对不同的阈值参数进行研究, 寻找最佳的阈值参数公式, 取得了满意的重建效果。

1 曲波变换

对地震数据f应用曲波变换会得到一系列曲波系数

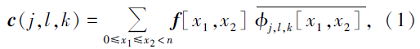
式中:ϕ 表示曲波变换, 系数c(j, l, k)分别表示曲波系数的尺度、方向和位置。对于复值曲波系数, 它是由两种不同的实值曲波变换函数的实部和虚部组成, 两种函数都具有相同的尺度、方位和位置, 但这两个函数彼此之间会有90° 相位差^[23]。实际上复值曲波变换函数算法几乎与实值曲波变换函数算法一样, 首先对信号进行实值曲波变换, 然后将具有相同尺度、方向和位置的实值曲波系数进行配对形成复值曲波系数, 实部和虚部都能表示信号的局部特征。根据Neelamani于2010年的研究^[24]得知:实值曲波变换所得到的曲波系数为实数, 曲波系数会产生一定的平移变化, 也即反射波位置的较小平移会导致实值曲波系数振幅的较大变化, 对信号损伤较大, 重建效果相对复值曲波较差。而复值曲波变换所得到的曲波系数用复数表示, 不会产生平移变化, 能有效地保护信号的主要特征, 重建后信噪比高, 但是运算时间是实值曲波变换的2倍, 为了得到较好的重建效果, 笔者采用复值曲波变换方法进行数据重建。

2 基于曲波变换和POCS算法

2.1 问题陈述

地震数据重建主要由随机缺失地震道记录通过线性算子的作用恢复出完整的地震数据。为此, 假设线性正演模型

$\begin{matrix} y_{obs} = Mf, (2) \end{matrix}$

其中:y_obs∈ Rⁿ代表随机缺失的地震数据; f∈ R^N, 且N≥ n, 表示待重建的完整地震数据; M∈ R^{n× N}为采样算子, 其元素0和1分别表示缺失道和已知道, 假设f在曲波域C中的稀疏表示是系数x, 则式(2)可以写成

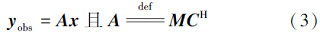
这里上标H代表共轭转置矩阵, 当从随机缺失的地震数据y_obs中重建出无假频数据f时, 由于x是稀疏的, 从而使得该欠定方程有解。

2.2 POCS重建算法

从以上分析可知, 数据重建的关键技术就是通过合适的数据重建方法来求解上述欠定问题 $\begin{matrix} ^{[2526]} \end{matrix}$ , 文中引入凸集投影算法进行求解, 重建的步骤如下:

1)选择合适的阈值参数λ _i(i=1, 2, …, N, 其中N为迭代次数), 给定一个初值y₀=y_obs, 即输入随机缺失的地震数据。

2)将随机缺失的地震数据y_i-₁作曲波变换x_i-₁=Cy_i-₁, 用λ _i作为阈值去除小于λ _i的值, 即x_i= $\begin{matrix} T_{λ_{i}} \end{matrix}$ Cx_i-₁, 下标i表示第i次迭代; $\begin{matrix} T_{λ_{i}} \end{matrix}$ 表示阈值算子。

3)将x_i作反曲波变换

$\begin{matrix} y_{i} = C^{H} x_{i}, (4) \end{matrix}$

然后将不完整地震数据y的未缺失地震数据填充到y_i上, 即

$\begin{matrix} y_{i} = (I - M) y_{i} + My, (5) \end{matrix}$

然后将得到的y_i代入步骤(2), 重新进行迭代, 直到运行N次迭代, 当精度满足要求时, 再对迭代N次后的x_n作逆曲波变换即可得到最终的重建结果。

2.3 阈值参数选取

由以上的重建步骤可知, 阈值参数的选取工作尤为重要。在POCS算法迭代过程中, 其阈值参数值一般从大到小进行变化, 即阈值参数λ _i满足:

$\begin{matrix} ‖ Cy ‖_{\infty} = λ_{1} > λ_{2} > \dots > ε, (6) \end{matrix}$

式中:ε 为接近零的小值, 由噪声能量决定, 不同地震数据ε 值有所差别。最早的研究中主要采用线性变化递减的阈值参数, 该阈值参数λ _i可由

$\begin{matrix} λ_{i} = λ_{\max} - \frac{(λ_{\max} - ε)}{N - 1} (i - 1) (7) \end{matrix}$

确定。式中:λ _max为|Cy|的最大值, 即稀疏变换系数绝对值的最大值。

后来有的学者又提出按e^-x(0≤ x≤ 1)指数规律衰减的阈值参数^[13], 该阈值参数为:

$\begin{matrix} λ_{i} = λ_{\max} \cdot e^{\frac{(i - 1) [\ln (ε) - \ln (λ_{\max})]}{N - 1}}, (8) \end{matrix}$

尽管该阈值参数收敛较快, 但仍然满足不了海量数据的处理。为此, 结合复值曲波变换, 选用按 $\begin{matrix} e^{- \sqrt[]{x}} \end{matrix}$ (0≤ x≤ 1)指数平方根规律衰减的阈值参数, 在保证精度的前提下, 使得收敛速度更快, 节省部分计算时间, 该阈值参数公式为:

$\begin{matrix} λ_{i} = λ_{\max} \cdot \exp \{[\ln (ε) - \ln (λ_{\max})] \sqrt[]{\frac{i - 1}{N - 1}}\} 。 (9) \end{matrix}$

3 理论模型

为了分析基于曲波变换和POCS算法重建的本质, 首先定义信噪比公式

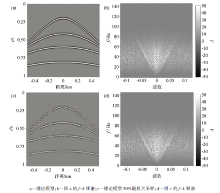
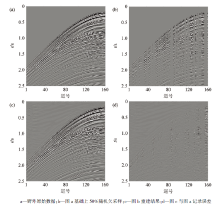
$\begin{matrix} R_{SN} = 20 \lg (‖ x_{0} ‖_{2} / ‖ x - x_{0} ‖_{2}), \end{matrix}$

其中:x₀表示原始数据模型, x表示重建结果, 信噪比越高, 代表重建结果与模型数据越接近, 重建效果越理想。图1a为采用40 Hz雷克子波合成的256道二维地震记录, 道距为4 m, 每道1 024个采样点, 采样间隔为1 ms, 数据合成时每一层反射波能量有所差异。图1b为原始地震记录的二维频谱。图1c为对理论模型50%欠采样后的地震剖面。图1d为图1c的f-k频谱, 从中可以看出由于采用了随机欠采样, 从而将由规则欠采样所引起的规则干扰转为不相干的随机噪声, 然后再采用合适的重建方法进行有效波信号提取, 恢复缺失地震道信息。为此, 拟通过复值曲波变换和POCS算法进行重建, 采用硬阈值算子进行处理, 以便恢复出缺失的地震道。

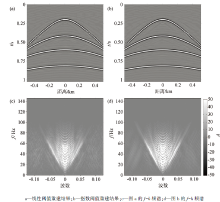
	Figure Option View Download New Window
	图1 原始模型采样及频谱

图2为采用线性阈值和指数阈值参数重建的结果及其f-k频谱, 重建后的信噪比分别为 11.07 dB和14.29 dB。图3为文中所提出的阈值参数重建结果及其f-k频谱, 重建后信噪比为14.94 dB, 其中迭代次数都为30次。从以上结果可以看出, 3种阈值参数重建效果都较好, 但是相比之下, 指数平方根阈值参数重建误差较少, 而且计算效率也更快。同时注意到, 由于随机欠采样完全随机, 地震道连续缺失且同相轴弯曲较大的有效波信号的恢复效果不好, 因此需要发展高维地震数据重建方法, 从另外一个空间方向进行信息弥补。

	Figure Option View Download New Window
	图2 不同阈值参数重建结果及频谱

	Figure Option View Download New Window
	图3 本文阈值重建结果(左)及其频谱(右)

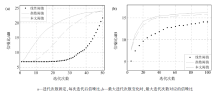
为了更详细地了解3种阈值参数重建后效果及其运算时间大小的关系, 仍然对理论模型进行50%随机欠采样后的数据进行重建。图4a表示最大迭代次数为50次时, 不同迭代次数与不同阈值参数重建后信噪比关系曲线, 可以看出每次迭代过程中阈值参数重建后信噪比最高, 其次是指数阈值参数, 最后才是线性阈值。图4b为最大迭代次数从5~100次变化, 计算出的每次最大迭代次数与重建后信噪比关系曲线。可以看出, 要想获得信噪比为14 dB的重建结果, 线性阈值需迭代93次左右, 指数阈值需迭代29次左右, 而笔者提出的阈值参数只需迭代18次左右, 可以节省一定的计算时间。为了再次说明指数阈值参数优势, 选用最大迭代次数分别为25、50、75、100、125、150时, 取得相同信噪比(R_SN=11 dB)时所对应的迭代次数表(表1), 可见每次都是阈值参数迭代次数最少。总体而言, 3种阈值参数重建后的信噪比都随迭代次数的增大而增加, 但在相同的精度下, 迭代次数太多会浪费计算时间, 从这方面来讲, 文中提取的阈值参数公式具有较大优势。而对于指数阈值和本文阈值参数, 从图4b可以看出, 当迭代次数大于30次后, 信噪比增加量随迭代次数增加相对较少, 并且当迭代次数超过60次以上时, 信噪比几乎不会再增加了, 因此从节省计算时间角度来看, 并不是迭代次数越多越好。文中采用30次迭代。

	Figure Option View Download New Window
	图4 不同方法重建信噪比曲线

表1 相同信噪比下3种阈值参数迭代次数比较(R_SN=11 dB)

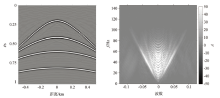
由于原始的地震数据在一定程度上都含有噪声, 所以需要检验在本文阈值参数下基于曲波变换和POCS重建算法的抗噪能力。为此, 在理论模型(图1a)中加入一定比例的随机噪声, 如果5a所示, 然后进行抗噪模拟实验, 图5b为50%一维随机欠采样示意, 图5c为在随机欠采样下采用本文方法的重建结果, 重建后信噪比5.13 dB, 图5d为重建前后的误差。通过对比可知, 含噪缺失地震道的全部信息都得到了较好的恢复, 且重建前后的有效信息几乎没有损失, 表明信号恢复效果较好, 从而也得出基于文中所提出的POCS算法和按指数平方根规律衰减的阈值参数在地震数据重建中, 具有良好的抗噪能力, 完全能够处理实际资料。

	Figure Option View Download New Window
	图5 50%地震道缺失的含噪地震数据及其重建结果

4 实际应用

图6a为野外某地区二维地震资料, 该数据道距25 m, 采样率4 ms, 180道接收, 由于时间采样长度为6 s, 为了节省处理时间, 截取了中间2.8 s进行处理。图6b为对理想采样记录进行50%一维随机欠采样, 然后采用本文方法对其进行重建, 重建后结果如图6c所示, 其信噪比为6.19 dB, 图6d为其误差剖面。从中可以看出, 在欠采样50%的情况下, 本文方法重建效果较好, 局部细节信息得到了较好的恢复, 弱能量有效波也得到较好的重建, 重建后同相轴几乎与原始地震记录一样, 能够满足后续其它处理的要求。图7分别表示原始地震数据、50%随机欠采样数据和重建后地震记录的f-k频谱, 从中也可以看出, 本文方法重建后f-k谱与真实频谱最为接近, 有效波能量损伤最小, 效果显著。

	Figure Option View Download New Window
	图6 50%地震道缺失的野外数据重建过程

	Figure Option View Download New Window
	图7 f-k频谱

5 结论

从以上研究可知, 传统的基于实值曲波变换和POCS算法的重建方法效果有限, 并且到达同样的重建精度时, 传统的阈值参数所需计算时间较多。而本文采用复值曲波变换和POCS算法进行数据重建, 提出采用按 $\begin{matrix} e^{- \sqrt[]{x}} \end{matrix}$ (0≤ x≤ 1)衰减规律的阈值参数, 最终构建出了基于复值曲波变换的地震数据重建技术。通过对比分析, 表明该方法具有参数设置简单、用时少、精度高等特点, 能够克服以往基于曲波变换重建方法的不足。

从文中的重建结果可以看出, 使用复值曲波变换作为稀疏基后, 数据重建效果具有明显的改善, 但与傅立叶变换相比, 运算时间增加近8倍, 特别是随着数据重建空间维数的增加, 所花费的计算时间更多, 从而使得在处理大量地震数据时受到一定限制, 因此也需要发展其他有效的快速算法, 在确保重建精度的同时减少运算时间, 以达到工业化生产的需要。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Herrmann F J. Rand omized sampling and sparsity: Getting more information from fewer samples[J]. Geophysics, 2010, 75(6): 173-187. [本文引用:1]
[2]	Trad D O. Five-dimensional interpolation: Recovering from acquisition constraints[J]. Geophysics, 2009, 74(6): 123-132. [本文引用:1]
[3]	Gao J, Sacchi M, Chen X H. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions[J]. Geophysics, 2013, 78(2): 21-30. [本文引用:1]
[4]	路交通, 曹思远, 董建华, 等. 基于稀疏变换的地震数据重构方法[J]. 物探与化探, 2013, 37(1): 175-179. [本文引用:1]
[5]	黄小刚, 王一博, 刘伊克, 等. 半径—斜率域加权反假频地震数据重建[J]. 地球物理学报, 2014, 57(7): 2278-2290. [本文引用:1]
[6]	张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5): 1637-1649. [本文引用:1]
[7]	Trad D, Ulryeh T, Sacchi M. Latest view of sparse radon transform[J]. Geophysics, 2003, 68(1): 386-399. [本文引用:1]
[8]	石颖, 柯璇, 王维红. 一种加权抛物Radon变换地震波场重建方法[J]. 物探与化探, 2012, 36(5): 846-850. [本文引用:1]
[9]	张振波, 轩义华. 高分辨率抛物线拉冬变换多次波压制技术[J]. 物探与化探, 2014, 38(5): 981-988. [本文引用:1]
[10]	唐欢欢, 毛伟建. 3D高阶抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2014, 57(9): 2918-2927. [本文引用:1]
[11]	Wang J F, Ng M, Perz M. Seismic data interpolation by greedy local Radon transform[J]. Geophysics, 2010, 75(6): 225-234. [本文引用:1]
[12]	薛亚茹, 唐欢欢, 陈小宏. 高阶高分辨率Radon变换地震数据重建方法[J]. 石油地球物理勘探, 201, 49(1): 95-101. [本文引用:1]
[13]	Jin S. 5D seismic data regularization by a damped least-norm Fourier inversion[J]. Geophysics, 2010, 75(6): 103-111. [本文引用:2]
[14]	Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. [本文引用:1]
[15]	白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. [本文引用:1]
[16]	冯飞, 王德利, 张亚红, 等. 结合曲波变换的焦点变换在地震数据去噪和插值中的应用[J]. 物探与化探, 2013, 37(3): 480-487. [本文引用:1]
[17]	薛永安, 王勇, 李红彩, 等. 改进的曲波变换及全变差联合去噪技术[J]. 物探与化探, 2014, 38(1): 81-86. [本文引用:1]
[18]	张广智, 郑静静, 印兴耀, 等. 基于Curvelet变换的角度流体因子提取技术[J]. 物探与化探, 2011, 35(4): 505-510. [本文引用:1]
[19]	张华, 陈小宏, 贺宗斌. 基于频率域复值曲波变换的三维地震数据重建[C]//北京: 中国地球科学联合学术年会, 2014: 1114-1118. [本文引用:1]
[20]	Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. [本文引用:1]
[21]	Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. [本文引用:1]
[22]	刘国昌, 陈小宏, 郭志峰, 等. 基于curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237-245. [本文引用:1]
[23]	Cand ès E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms[J]. SIAM Multiscale Modeling and Simulation, 2006, 5(1): 861-899. [本文引用:1]
[24]	Neelamani R, Baumstein A, Ross W S. Adaptive subtraction using complex-valued curvelet transforms[J]. Geophysics, 2010, 75(4): 51-60. [本文引用:1]
[25]	王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重建[J]. 石油地球物理勘探, 2015, 50(1): 20-28. [本文引用:1]
[26]	Zhang H, Chen X H, Li H X. 3D seismic data reconstruction based on complex-valued curvelet transform in frequency domain[J]. Journal of Applied Geophysics, 2015, 113(6): 64-73. [本文引用:1]

2010

0.0

2009

0.0

... 常用的数据重建方法主要有基于某种数学变换的插值技术,例如Radon变换 912、傅里叶变换^[2,13]、Curvelet变换 1419等 ...

2013

0.0

2013

0.0

路交通, 曹思远, 董建华, 等. 基于稀疏变换的地震数据重构方法[J]. 物探与化探, 2013, 37(1): 175-179.

The seismic data recovery from data with missing traces plays an important role in the later stage seismic processing.The authors studied the sparse transform (F-K transform and Curvelet transform) and popular compressed sensing theory,and then combined the two methods together to build the seismic data recovery model which is based on sparse transform.The F-K transform changes the seismic data from the t-x (time-space) domain into the f-k (frequency-wavenumber) domain.Because of the favorable directionality and locality and multidimensionality,the curvelet transform can represent the seismic data in a more compressible way.On the basis of the recovery model,the missed seismic data are recovered by the two sparse transforms and the recovery results are compared and analyzed.The recovery results prove that the Curvelet transform recovery can get the better reconstruction effect than the F-K transform.Finally the Marmousi2 model and practical seismic data are processed,and the result shows that the seismic data recovery model is correct and effective.

缺失地震数据重构恢复是后期地震资料处理取得良好效果的前提。笔者通过研究稀疏变换(F-K变换、Curvelet变换)与最近流行的压缩感知理论,将两者结合起来,建立基于稀疏变换的地震数据重构模型。F-K变换是将地震数据由时间—空间域变换到稀疏域频率—波数域,Curvelet变换由于其良好的方向性、局部性以及各向异性,能够将地震数据进行更优的稀疏表达。基于重构模型,分别采用这两种稀疏变换对地震数据进行重构,并且比较两者的重构效果,证实Curvelet变换重构效果优于F-K变换。最终通过Marmousi 2模型以及实际地震资料处理分析,证明该重构模型的正确性和有效性。

2014

0.0

黄小刚, 王一博, 刘伊克, 等. 半径—斜率域加权反假频地震数据重建[J]. 地球物理学报, 2014, 57(7): 2278-2290.

In order to reduce the influence of the missing seismic traces on the follow-up seismic processes, seismic data reconstruction is required. To solve the problem of anti-alias seismic data reconstruction, some research about this was done and a new method called weighted anti-alias seismic data reconstruction in R-P (radius-slope) domain is proposed. The F-K (frequency-wave number) spectra are transformed to the R-P domain and a weighting function is designed. During every iteration process of the reconstruction, the R-P spectra are modified by the weighting function. By testing with synthetic and field data, the capacity of anti-alias reconstruction of this method is proved.

[Huang Xiao-Gang; Wang Yi-Bo; Liu Yi-Ke; Chang Xu] Chinese Acad Sci, Inst Geol & Geophys, Key Lab Engn Geomech, Beijing 100029, Peoples R China.;[Huang Xiao-Gang] Univ Chinese Acad Sci, Beijing 100049, Peoples R China.

为减小地震数据缺失给地震后续处理工作带来的影响，需要对地震数据进行插值重建.针对反假频插值重建这个难点问题，进行了相关研究，并由此提出了一种改进的 R-P （半径-斜率）域加权反假频地震数据插值重建方法.该方法将 F-K （频率-波数）谱变换到 R-P 域，在 R-P 域设计一个权函数并将其作用于每次的迭代插值过程.通过模型数据和实际数据的测试，证明了该方法具有较好的反假频插值重建能力.

2013

0.0

张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5): 1637-1649.

Traditional seismic data sampling must follow the Nyquist sampling theorem, while the field data acquisition can't meet the sampling theorem due to missing traces or exploration cost limit, so there exits data reconstruction problem. In this paper, based on the theory of compressed sensing, we render coherent aliases of regular under-sampling into harmless incoherent random noise using the random under-sampling, effectively turning the reconstruction problem into a much simpler de-noising problem. We introduce the Projections Onto Convex Sets (POCS) algorithm during the process of reconstruction, choosing the square root exponentially decreased threshold, constructing a curvelet-based recovery strategy of 3D seismic data. At the same time, aiming at the deficiency of simple random under-sampling, we introduce the jittered under-sampling, it shares the benefits of random sampling and controls the maximum gap size. Experiments show that reconstruction effect based on curvelet is better than FFT transform and jittered under-sampling is better than random under-sampling. At last, we apply this technology into practical seismic data and obtain a good application.

传统的地震勘探数据采样必须遵循奈奎斯特采样定理,而野外数据采样可能由于地震道缺失或者勘探成本限制,不一定满足采样定理要求,因此存在数据重建问题.本文基于压缩感知理论,利用随机欠采样方法将传统规则欠采样所带来的互相干假频转化成较低幅度的不相干噪声,从而将数据重建问题转为更简单的去噪问题.在数据重建过程中引入凸集投影算法(POCS),提出采用 e -√ x (0≤ x ≤1)衰减规律的阈值参数,构建基于曲波变换三维地震数据重建技术.同时针对随机采样的不足,引入jitter采样方式,在保持随机采样优点的同时控制采样间隔.数值试验表明,基于曲波变换的重建效果优于傅里叶变换,jitter欠采样的重建效果优于随机欠采样,最后将该技术应用于实际地震勘探资料,获得较好的应用效果.

2003

0.0

2012

0.0

石颖, 柯璇, 王维红. 一种加权抛物Radon变换地震波场重建方法[J]. 物探与化探, 2012, 36(5): 846-850.

A weighted parabolic Radon transform approach is proposed based on the basic principle and computation method of conventional band-limited forward and inverse parabolic radon transform.The proposed algorithm is applied to prestack seismic wavefield restoration and reconstruction,such as the missing offset interpolation and anti-alias resampling in the offset direction;The weight coefficient is determined by seismic data in x-τ domain,i.e.,the weight coefficient varies in different iteration processes.For the seismic data from uniform sampling,this paper gives the reconstruction result of missing near offset extrapolation and resampling for anti-alias seismic data.The test results demonstrate that the presented weighted parabolic radon transform is effective for seismic wavefield reconstruction,with the characteristics of robustness,high precision and high efficiency.

基于带限正反抛物Radon变换的基本原理和计算方法,笔者给出了一种加权抛物Radon变换(PRT)算法,该方法可应用于叠前地震波场恢复和重建,如缺失偏移距地震数据的插值外推和反假频重采样,其权系数完全由数据域来确定,也就是说在迭代计算过程中,该权系数也在变化。对于均匀采样的地震数据,笔者给出了近偏移距外推和波场的反假频重采样的计算结果,试算表明笔者给出的加权PRT方法可有效地应用于地震波场重建中,并具有算法稳健、计算精度高和效率高的特点。

2014

0.0

张振波, 轩义华. 高分辨率抛物线拉冬变换多次波压制技术[J]. 物探与化探, 2014, 38(5): 981-988.

Conventional parabolic radon transform method cannot attenuate the multiples ideally and causes spatial alias for the short spread and sparse sampling seismic data. After analyzing the papers by Sacchi, Mauricio, Todd Mojesky and some other researchers. on multiples attenuation by using parabolic radon transform method, this paper describes the theory of high resolution parabolic radon transform method. The result shows that the high resolution parabolic radon transform method can efficiently and effectively realize spatial anti-alias multiples suppression after the new method is applied to the model data and real seismic data respectively; meanwhile, this method can overcome the limitation of insufficient samples and short offset.

对于孔径过小，采样不充分的地震数据，抛物线拉冬变换的多次波压制效果不理想，且存在空间假频问题。综合Sacchi、Mauricio、Todd Mojesky等对抛物线拉冬变换压制多次波的分析，阐明了高分辨率抛物线拉冬变换原理。通过理论模型试验和实际地震数据的分析证明，高分辨率抛物线拉冬变换可以突破离散采样和有限孔径的限制，实现对地震数据中的多次波及空间假频的快速、有效压制。

2014

0.0

唐欢欢, 毛伟建. 3D高阶抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2014, 57(9): 2918-2927.

3D high-order parabolic Radon transform (HOPRT) method for amplitude preserving reconstruction is proposed on the basis of the traditional 3D parabolic Radon transform and orthogonal polynomial fitting techniques. The information on the amplitude and its gradient and curvature of the AVO data are taken into account in the 3D parabolic Radon transform, which makes the proposed method have higher accuracy for AVO data. We present a workflow for seismic data reconstruction with amplitude preserved by the method of HOPRT. The results of the synthetic model and the field data demonstrate the effectiveness of the method.

本文结合传统3D抛物Radon变换（PRT）和AVO数据正交多项式拟合，给出了3D高阶抛物Radon变换方法（HOPRT）.该变换增加了描述AVO数据变化的梯度信息和曲率信息，拓展了传统3D抛物Radon变换方法，使其在具有AVO特征的数据重建中具有更高的准确度，从而提高AVO分析的可靠性.文中给出了3D高阶抛物Radon变换进行地震数据保幅重建的流程.理论模型和实际地震资料的重建结果显示了本文方法的优点.

2010

0.0

薛亚茹, 唐欢欢, 陈小宏. 高阶高分辨率Radon变换地震数据重建方法[J]. 石油地球物理勘探, 201, 49(1): 95-101.

Missing seismic data will affect seismic data processing and interpretation. Considering the reflection wave amplitude lateral continuity along events, we propose a high order high resolution Radon transform for seismic data reconstruction. Radon transform is only summation along events, and our method incorporates it with orthogonal polynomial transform and gets the gradient and curvature information of events. The high order high resolution Radon transform takes advantage of both velocity distinction of Radon transform and preserves AVO information of orthogonal polynomial transform. Tests on model data and real seismic data show that this method can achieve anti-aliasing, data reconstruction, and AVO information preservation.

地震数据缺失会影响处理和解释结果。本文基于Radon变换地震数据重建并结合地震波同相轴横向连续性，提出高阶高分辨率Radon变换地震数据重建方法。该方法将正交多项式变换和Radon变换结合，通过正交多项式变换拟合地震波振幅随炮检距变化特性，改进了传统Radon变换只考虑地震道叠加特性的缺陷，增加了振幅变化的斜率和曲率信息，保留了地震波AVO特性，有利于地震波振幅信息在横向变化情况下缺失地震数据的重建。理论模型和实际数据处理结果表明，该方法可以克服空间假频，实现缺失道数据重建，并保留振幅AVO信息。

2010

0.0

... 常用的数据重建方法主要有基于某种数学变换的插值技术,例如Radon变换 912、傅里叶变换^[2,13]、Curvelet变换 1419等 ...

... 1)指数规律衰减的阈值参数^[13],该阈值参数为: ...

2008

0.0

2014

0.0

白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945.

由于野外采集环境的限制,常常无法采集得到完整规则的野外地震数据,为了后续地震处理、解释工作的顺利进行,地震数据重建工作被广泛的研究.自压缩感知理论的提出,相继出现了基于该理论的多种迭代阈值方法,如CRSI方法(Curvelet Recovery by Sparsity promoting Inversion method)、Bregman迭代阈值算法(the linearized Bregman method)等.CSRI方法利用地震波形在Curvelet的稀疏特性,通过一种基于最速下降的迭代算法在Curvelet变换域恢复出高信噪比地震数据,该迭代算法稳定,收敛,但其收敛速度慢.Bregrnan迭代阈值法与CRSI最大区别在于每次迭代时把上一次恢复结果中的阈值前所有能量都保留到本次恢复结果中,从而加快了收敛速度,但随着迭代的进行重构数据中噪声干扰越来越严重,导致最终恢复出的数据信噪比低.综合两种经典方法的优缺点,本文构造了一种新的联合迭代算法框架,在每次迭代中将CRSI和Bregman的恢复量加权并同时加回本次迭代结果中,从而加快了迭代初期的收敛速度,又避免了迭代后期噪声干扰的影响.合成数据和实际数据试算结果表明,我们提出的新方法不仅迭代快速收敛稳定,且能得到高信噪比的重建结果.

2013

0.0

2014

0.0

2011

0.0

2014

0.0

2006

0.0

2010

0.0

2011

0.0

... 刘国昌等^[22]采用曲波变换作为稀疏基,相比于二维傅立叶变换,该方法更能够重建非线性同相轴,更加适合具有各向异性特征的地震波场,但他没有对阈值参数选择作进一步研究 ...

2006

0.0

... 相位差^[23] ...

2010

0.0

... 根据Neelamani于2010年的研究^[24]得知:实值曲波变换所得到的曲波系数为实数,曲波系数会产生一定的平移变化,也即反射波位置的较小平移会导致实值曲波系数振幅的较大变化,对信号损伤较大,重建效果相对复值曲波较差 ...

2015

0.0

2015

0.0