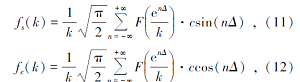引用本文
李锋平, 杨海燕, 邓居智, 汤洪志, 刘旭华, 赵海娇. TEM正演响应计算的几种频-时域转换方法对比[J]. 物探与化探, 2016,40(4): 743-749.
LI Feng-Ping, YANG Hai-Yan, DENG Ju-Zhi, TANG Hong-Zhi, LIU Xu-Hua, ZHAO Hai-Jiao. Comparison of several frequency-time transformation methods for TEM forward modeling[J]. Geophysical and Geochemical Exploration, 2016,40(4): 743-749.
Doi:10.11720/wtyht.2016.4.17  
Permissions
Copyright©2016, 《物探与化探》编辑部
《物探与化探》编辑部 所有
TEM正演响应计算的几种频-时域转换方法对比
李锋平, 杨海燕, 邓居智, 汤洪志, 刘旭华, 赵海娇
东华理工大学 放射性地质与勘探技术国防重点学科实验室,江西 南昌 330013
通讯作者: 杨海燕(1980-),男,博士,副教授。2009年博士毕业于中国矿业大学地球探测与信息技术专业,主要从事电磁法勘探方面的理论与应用研究。E-mail:genious_yang@126.com

作者简介: 李锋平(1989-),男,江西井冈山人,汉族,在读硕士研究生,研究方向为电磁法勘探理论与应用。E-mail: geophysics_Lee@163.com

收稿日期: 2016-01-12
基金: 江西省自然科学基金项目(20151BAB203045); 江西省教育厅科学技术研究项目(GJJ14487); 放射性地质与勘探技术国防重点学科实验室开放基金(RGET1308)和国家自然科学基金项目(41564001, 41164003, 41264004, 41174107)联合资助
摘要

在瞬变电磁的一维正演响应模拟中,常用的方法是先在频率域中求解,之后将结果转换到时间域。但该方法在晚期的计算精度通常不高,因此,使用5种频-时域转换方法(正、余弦变换的数值滤波算法,G-S逆拉普拉斯算法、正、余弦变换的折线逼近法)进行了计算,与解析解对比,得出余弦变换的数值滤波算法在晚期计算中精度最高的结论,并对这五种转换方法产生误差问题的原因进行了讨论和分析。本研究有利于瞬变电磁一维正演响应的高精度计算,使其在多维计算中得到更好的应用。

关键词: 瞬变电磁; 频李凤平-时域转换; 数值滤波; G-S逆拉普拉斯算法; 折线逼近
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)04-0743-07 doi: 10.11720/wtyht.2016.4.17
Comparison of several frequency-time transformation methods for TEM forward modeling
LI Feng-Ping, YANG Hai-Yan, DENG Ju-Zhi, TANG Hong-Zhi, LIU Xu-Hua, ZHAO Hai-Jiao
Fundamental Science on Radioactive Geology and Exploration Technology Laboratory,East China University of Technology,Nanchang 330013,China
Abstract

In the forward modeling of transient electromagnetic response, the commonly used method is to calculate the response in the frequency domain, and then the results were converted into the time domain. In this paper, five frequency-time conversion methods (Digital filtering algorithms of sine and cosine transform, G-S inverse Laplace algorithm, polygonal approximations method of sine and cosine transform) were used to conduct calculation. it is concluded that the digital filtering method based on cosine transform has the highest computing precision among these five methods, as shown by the comparison with the analytical algorithm, and the reasons of the error caused by these five kinds of conversion methods were discussed and analyzed, which is beneficial to the high precision calculation of one-dimensional forward modeling of transient electromagnetic response, so that these methods can be better applied to the calculation of multi-dimensional frequency-time conversion.

Keyword: transient electromagnetic; frequency-time conversion; digital filtering; G-S inverse Laplace algorithm; polygonal approximations

瞬变电磁法正演响应的计算一般都是先求得频率域的解, 然后由频率域转换到时间域得到瞬态解 然后由频率域转换到时间域得到瞬态解[1-5]。目前, 可用于频 时域转换的方法较多, 且各具特色。傅立叶变换是最早应用于其中的方法, 但傅立叶变换过程中要求频率的采样点数必须满足采样定理, 这样频率采样点会增多, 从而造成计算量加大, 计算速度减慢[6]。Anderson于1974年应用改进的离散傅立叶变换对任意层状地电断面的瞬变电磁测深响应的正演计算进行了研究[7]; Guptasarma在1982年提出用于计算时间域激电响应的线性滤波算法, 把频率域中如Cole-Cole这些包含复频变量分数指数的阻抗模型的电压响应转换到阶跃电流激励下时间域的电压响应; 另外, Anderson提出滞后褶积快速滤波方法; Knight和Raiche在1982年提出Gaver-Stehfest算法用于电磁场的时频转换[10]; 长谷川健对电偶源发射由磁场定义的瞬变测深视电阻率响应进行了正演计算[11]; Newman于1986年提出延迟谱法用于瞬变电磁响应的计算[12]; 考夫曼 A.A.和凯勒 G.V.在1987年提出余弦变换用于瞬变电磁场响应计算的频 -时域转换, 余弦变换有多种算法, 比如费龙算法、折线逼近算法和数值滤波算法 -。国内长期致力于研究瞬变电磁法的专家朴化荣教授对Gaver-Stehfest进行了改进, 提出Gaver-Stehfest逆拉普拉斯算法[15]; 陈乐寿、王光锷于1991年用数字滤波方法计算了瞬变电磁的响应[16]; 李吉松、朴化荣对考夫曼 A.A.和凯勒 G.V.提出的余弦变换算法进行了适当修改, 取得了较好计算效果[17]; 罗延钟、昌彦君提出新的G-S变换算法, 提高了电磁场瞬变响应的计算速度[18]; 王华军基于贝赛尔函数与正余弦函数之间的关系和成熟的快速汉克尔变换理论, 导出了正、余弦变换的数值滤波算法[19]; 陈入云、向淑晃在最速下降法的基础上, 提出了一种正余弦变换的改进高效算法[20]; 徐振平提出基于数值滤波的逆Laplace变换算法进行瞬变电磁正演响应的计算, 得到了大时间范围内的收敛解[21]。

Gaver-Stehfest算法的精度与计算机环境字长密切相关, 字长越大精度越高, 因此该算法对计算机硬件和软件要求较高 2223; 使用折线逼近算法时, 积分步长难以控制, 需要采用误差控制步长[24]; 在使用数值滤波计算时常用到高振荡积分形式的正、余弦变换, 用经典积分方法如高斯积分法去求解不适用, Levin型方法、广义积分方法、数值最快下降法、费龙算法都存在处理过程复杂、计算精度满足不了要求的缺陷。因此, 高振荡问题的理论与计算被公认为是科学计算领域最具挑战性研究领域之一[25]。

为此, 笔者针对中心回线装置, 在均匀半空间情况下, 使用多种频 -时域转换方法(正、余弦变换的数值滤波算法, G-S逆拉普拉斯算法, 正、余弦变换的折线逼近法)计算均匀大地表面的感应电压值, 然后将计算结果与均匀半空间的解析解进行了对比分析, 优选算法, 力求对其做出一个全面细致的归纳总结, 从而使其在瞬变电磁多维正演计算中得到更好的应用。

1 几种频-时域转换方法的简介

1.1 G-S逆拉普拉斯算法

Gaver-Stehfest逆拉普拉斯算法的主要思想即利用δ 函数的基本积分性质, 让变换函数本身和它跟δ 函数乘积的积分联系在一起, 然后选择恰当的δ 函数使得积分形式转换为和变换函数的拉普拉斯变换相关的形式。这样就可利用熟悉的拉普拉斯变换式求取原函数, 从而达到逆变换的目的[26]。

1982年, Knight及Raiche 首先提出了Gaver-Stehfest 算法。朴化荣教授随后提出了Gaver-Stehfest 逆拉普拉斯算法, 其计算表达式为[27]

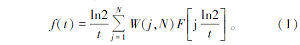
在阶跃电流激励的情况下, 中心回线装置感应电动势的计算表达式为[28]

V(t)=2πC1∫0∞Re[Hz(ω)]cos(ωT)dω。(2)

中心回线装置情况下, 二次场磁场分量对时间的导数的可以表示为[29]

∂H(t)∂t=-2π∫-∞∞ImHz(ω)sin(ωt)dω, (3)

因此, 根据法拉第感应定律, 中心回线装置感应电动势的计算表达式还可表述为

V(t)=2πC1∫0∞Im[Hz(ω)]sin(ωT)dω。(4)

对式(2)进行Gaver-Stehfest 逆拉普拉斯变换, 可以得到感应电动势V(t)的表达式

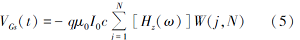
式中:j=1, 2, 3, …; N是抽样点的位置; q是有效接收面积; c=ln2/t, 是采样间隔; W(j, N)是Gaver-Stehfest变换的系数。

1.2 正、余弦变换的折线逼近法

折线逼近法的思想是把足够光滑的F(ω )函数曲线分成N段(N的大小取决于函数F(ω )的分布形态和计算精度), 并在每个段内用折线去进行逼近F(ω )。若函数F(ω )的曲线愈是光滑, 分段越是细致, 其逼近误差即可达到足够小[30]。

根据前面所述原理, 其数值计算表达式分别为[31]

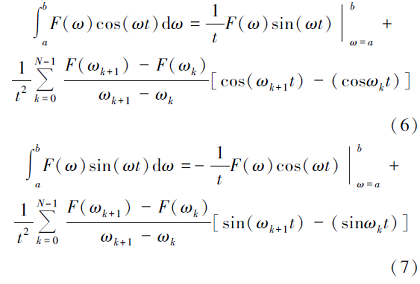
其中, a和b为积分的上、下限, ω 为采样角频率, t为采样时间。则中心回线装置的感应电动势的正、余弦折线逼近的计算近似表达式分别为:

正弦变换的折线逼近形式

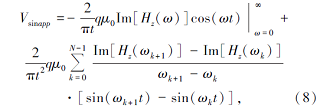
余弦变换的折线逼近形式

其中:N将积分区间分成N段, N的大小要考虑Re[Hz(ω )]和Im[Hz(ω )]的分布形态和计算精度; q为线圈有效接收面积。

1.3 正、余弦变换的数值滤波算法

根据贝塞尔函数与正余弦函数之间存在的如下关系[32]:

J-1/2(z)=2πzcos(z), J12(z)=2πzsin(z)(10)

带正、余弦的积分式可转化为求解贝塞尔函数积分式, 运用成熟的快速汉克尔变换理论, 得到正、余弦变换的数值滤波算法[19]

其中:采样间隔Δ =ln(10)/20, csin(nΔ )、ccos(nΔ )分别为正、余弦变换的数值滤波系数。

中心回线装置情况下, 在阶跃电流激励情况下, 经推导可得其感应电动势的计算表达式为:

正弦积分形式

Vsin(t)=-2qμ0π∫0∞Im[H(ω)]sin(ωt)dω, (13)

余弦积分形式

Vcos(t)=2qμ0π∫0∞Re[H(ω)]cos(ωt)dω, (14)

其中:q为有效接收面积, 计算时采用王华军给出的250点正、余弦变换滤波系数。

2 精度验证及误差分析

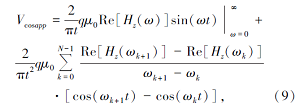
根据美国地球物理学家P.Raab和F.Frisehknecht推出的均匀半空间中心回线装置的感应电压的解析表达式[28]

V(t)=qIπ32ρL3[3Φ(z)-(3z+2z3)Φ˙(z)]u(t), (15)

式中:z= 2πL/τ ; τ = 2πρ×107; L是发射线圈边长; q是接收线圈的有效面积; I是激发电流; ρ 是大地电阻率; Φ (z)称为余误差函数; Φ˙(z)=(2/ π)exp(-z2); u(t)=1。用式(15)来验证上一节的数值算法的精度。

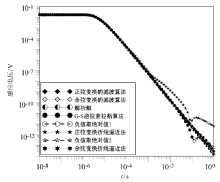
令发射回线边长为100 m, 接收面积为1 m2, 置于电阻率为100 Ω · m的均匀大地表面上, 供电电流为 1 A, 在t=0时切断, 得到解析解和以上5种频 时域转换数值算法的计算结果(图1), 采样时间段为1.0E-08~1s。计算了5种转换算法相对于解析解的相对误差(图2, 图3), 图中相对误差由100%× (V数值解-V解析解)/V解析解计算得到。另外, 还计算了半空间下5种转换方法的计算结果相对于解析解的平均相对误差(表1), 表中△ 1、△ 2、△ 3、△ 4、△ 5分别为正弦变换的滤波算法、余弦变换的滤波算法、G-S逆拉普拉斯算法、正弦变换的折线逼近法、余弦变换折线逼近法的平均相对误差, 平均相对误差由(所有采样时刻点的相对误差之和)/(采样时刻点个数)计算得到。

图1 5种时-频转换算法计算的感应电压曲线

图2 4种时-频转换算法计算的感应电压相对误差曲线

图3 正弦变换的折线逼近法计算的感应电压相对误差曲线

表1 半空间下5种算法计算结果的平均相对误差 %

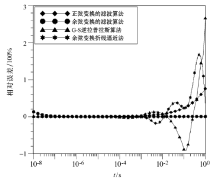
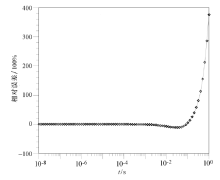
从图1可以看出, 除了正弦变换的折线逼近法, 其余四种转换方法的计算结果曲线和解析解的曲线都比较吻合, 同时, G-S逆拉普拉斯算法和正弦变换的折线逼近法的计算结果晚期部分出现了负值现象(如图中所示的负值取绝对值1和负值取绝对值2曲线, 结果为负数, 取绝对值后呈现在图上。), 而其余方法则没有这种情况。从图2和图3以及表1可以看出, 除余弦变换的滤波算法在早期高频段(106~108 Hz)出现了一定相对误差, 其余方法都有很高的转换精度, 但瞬变电磁法实际观测的采样时间范围一般在n× (10-3~102) ms, 所以这个影响可以忽略; 另外, 从以上图表不难看出, 正弦变换的折线逼近法的相对误差是最大的, 特别是在晚期时段, 最高达到了接近380× 100%的相对误差, 而余弦变换的滤波算法的转换精度在10-6~1 s时间段是最好的, 相对误差接近零, 和解析解曲线基本吻合, 在10-8~1 s或是10-6~1 s时间段的平均相对误差也分别只有0.83%和 0.08%, G-S逆拉普拉斯算法、正弦变换的滤波算法、余弦变换的折线逼近法依序次之。

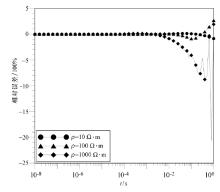
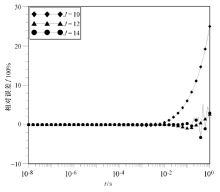
下面对5种准换方法产生误差问题的原因进行讨论。对于G-S逆拉普拉斯算法, 其要求双精度运算, 李建慧等认为G-S算法的精度与滤波系数J的取值、计算机字长有关。计算机字长越大, J的取值相应变大, G-S算法的精度就会越高[34]。通过试算, 发现其计算精度还与大地电阻率值有关, 图4为在滤波系数值J相同的情况下, 大地电阻率分别为10、100、1 000 Ω · m时, G-S逆拉普拉斯算法计算的感应电压相比于解析解的相对误差曲线, 从图中可以看出, 随着大地电阻率值的增大, 其相对误差也相应增大; 另外, 图5为在滤波系数值J不同的情况下, G-S逆拉普拉斯算法计算的感应电压相比于解析解的相对误差曲线, J的取值分别为10、12、14, 当J=12时, 其计算结果的相对误差相对较小。因此, 在实际运用中应根据所用计算机的有效字长选取最适合的滤波系数。

图4 不同电阻率G-S逆拉普拉斯算法计算的感应电压相对误差曲线

图5 不同滤波系数G-S逆拉普拉斯算法计算的感应电压相对误差曲线

从式(6)和式(7)可以看出, 正、余弦变换的折线逼近法中含有sin(ω t)和cos(ω t)项, 当角频率ω 和采样时间t比较大时, sin(ω t)和cos(ω t)会强烈震荡(如图6所示, 其中ω =105), 这样, 就需要将F(ω )函数曲线分成更多的段来逼近原函数, 分段越多, 其计算精度越高。但是这种分段还取决于F(ω )函数的分布形态, 不是很好确定。在瞬变电磁中, 分段越多, 意味着采样时刻点个数的增多, 其个数可能超过几千甚至几万个。从图7可以看出, 对于正弦变换的折线逼近法, 随着分段数N的增大, 其相对误差并没有太大变化, 尤其是在10-1 s后, 其差别不是很大; 而对于余弦变换的折线逼近法, N从200增大到6 000时, 其整体相对误差的改变还是很可观的, 但当N从6 000增大到 50 000时, 在10-1s后, 其相对误差也没有太大的变化。由于这两种方法需要的采样点数都相对比较大, 在实际运用中不可取。

图6 高震荡函数sin(ω t)和cos(ω t)的曲线

图7 N不同时正、余弦变换的折线逼近法计算的感应电压相对误差曲线

正、余弦变换的滤波算法都是基于正、余弦变换是汉克尔变换的特例, 运用成熟的汉克尔变换理论推导而得, 从理论上讲, 两者都是等效的, 但两者的转换结果却相差很大, 特别是在低频晚期段, 余弦变换的滤波算法精度很高, 而在高频段出现了一定的相对误差, 正弦变换的滤波算法则反之。原因是在频域到时域的转换时, 正弦变换的滤波算法计算(公式(13))采用的核函数是垂直磁场的虚分量, 即ImHz(ω ), 此核函数在早期高频段(108~106 Hz)函数曲线比较光滑, 斜率变化不大(如图8a所示, 图中虚线为负数取绝对值后的数), 所以, 在早期高频段, 计算精度比较理想; 但随着频率的减小, 在(106~1 Hz)频段, 曲线斜率迅速增大(如图8b所示, 图中虚线为负数取绝对值后的数), 虽然函数曲线依然光滑, 但因是负数, 所以导致计算结果会缓慢大于解析解, 因而在晚期低频段出现了较大的相对误差。反观余弦变换的滤波算法(公式(14)), 采用的核函数是垂直磁场的实分量, 即ReHz(ω ), 此核函数在早期高频段(108~106 Hz)出现了正负交替剧烈震荡的现象(如图8a所示), 随着频率的继续减小, 在(106~1 Hz)频段其曲线变得很光滑(如图8b所示), 104 Hz之后函数曲线的斜率几乎趋于零, 其值不再发生变化。因此, 余弦变换的滤波算法的计算结果在晚期低频段精度很高, 且瞬变电磁法实际观测的采样时间范围一般在n× (10-3~102) ms, 在这个范围内余弦变换的滤波算法的相对误差近乎为零, 所以在高频段出现的相对误差不会影响实际观测。

图8 发射回线中心处垂直磁场(Hz(ω ))随频率变化曲线

3 结论和建议

1) 正弦变换的数值滤波算法由于核函数 Im(Hz(ω ))的性质, 在早期高频段的计算有优势, 精度较高, 但是在晚期低频段计算结果出现了一定的相对误差, 转换精度不是很理想。

2) 余弦变换的数值滤波算法的转换精度在瞬变电磁法实际的采样时间范围内明显高于其它四种方法, 可以满足对转换精度的要求。

3) G-S逆拉普拉斯算法转换精度与滤波系数J的取值、计算机字长、大地电阻率等有关, 但其计算精度总体上来说较好, 仅次于余弦变换的数值滤波算法, 且计算速度非常快, 在实际运用中比较有优势。

4) 正弦变换的折线逼近法在晚期低频段的计算结果相对误差非常大, 且加大采样频点数其转换精度提升得不是很明显, 其计算速度也较慢, 不适合在实际应用中使用。

5) 余弦变换的折线逼近法在晚期低频段的计算结果相对误差明显小于正弦变换的折线逼近法的计算结果, 虽然加大采样频点数其转换精度提升的比较大, 但增加了运算时间, 也不适合在实际运用中使用。

在瞬变电磁一维正演响应计算时, 首先必须确保频率域的计算结果有足够的精度, 然后在此基础上采用更高计算精度, 效率更好的频 时域转换方法, 从目前来看, 余弦变换的数值滤波算法和G-S逆拉普拉斯算法都是比较好的选择。因此, 在进行瞬变电磁法多维正演模拟时, 利用数值方法计算出频率域电磁响应后, 可使用余弦变换的数值滤波算法或G-S逆拉普拉斯算法获得时间域电磁响应, 并根据各算法的特点, 使其在多维问题的正演计算中得到更好的应用。

The authors have declared that no competing interests exist.

参考文献
[1] Misac N. Nabighian. Quasi-static transient response of a conducting half-space: An approximate representation[J]. Geophysics, 1979, 44(9): 1700-1705. [本文引用:1]
[2] Ali Moradi Tehrani. Quasi-analytcal method for frequency-to-time conversion in CSEM applications[J]. Geophysics, 2012, 77(5): 357-363, doi: DOI:10.1190/GEO2011-0432.1. [本文引用:1]
[3] 李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002. [本文引用:1]
[4] 薛国强, 李貅, 底青云. 瞬变电磁法理论与应用研究进展[J]. 地球物理学进展, 2007, 22(4): 1195-1200. [本文引用:1]
[5] 薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 2008, 23(4): 1165-1172. [本文引用:1]
[6] 昌彦君, 张桂青. 电磁场从频率域转换到时间域的几种算法比较[J]. 物探化探计算技术, 1995, 17(3): 25-29. [本文引用:1]
[7] 陈向斌, 胡社荣, 张超. 瞬变电磁场响应计算的频-时域转换方法综述[J]. 工程地球物理学报, 2008, 5(2): 242-246. [本文引用:1]
[8] Guptasarma D. Computation of the time-domain response of a polarizable ground[J]. Geophysics, 1982, 47(11): 1574-1576, doi: DOI:10.1190/1.1441307. [本文引用:1]
[9] 阮百尧. Guptasarma算法在瞬变电磁正演计算中的应用[J]. 桂林工学院学报, 1996, 16(2): 167-170. [本文引用:1]
[10] Knight J H, Raichei A P. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method[J]. Geophysics, 1982, 47(1): 47-50. [本文引用:1]
[11] 长谷川健. 水平电气双极子によろ层状大地のスチツア应答と见挂导电率について[J]. 物理探查, 1985, 38(3): 21-31. [本文引用:1]
[12] Newman G A, Hohmann G W, Anderson W L. Transient electromagnetic response of three-dimensional body in a layered earth[J]. Geophysics, 1986, 51(8): 1680-1626. [本文引用:1]
[13] Kaufman A A, Keller G V. Frequency and transient sounding(in chinese)[M]. Beijing: Ecological Publishing House, 1987. [本文引用:1]
[14] 李建慧, 朱自强, 曾思红, 等. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 2012, 27(4): 1393-1400. doi: DOI:10.6038/j.issn.1004-2903.2012.04.013. [本文引用:1]
[15] 朴化荣. 电磁测深法原理[M]. 地质出版社, 1990. [本文引用:1]
[16] 陈乐寿, 王光锷. 构造电法勘探[M]. 武汉: 中国地质大学出版社, 1991, 1-203. [本文引用:1]
[17] 李吉松, 朴化荣. 电偶源瞬变测深一维正演及视电阻率响应研究[J]. 物探化探计算技术, 1993, 15(2): 108-116. [本文引用:1]
[18] 罗延钟, 昌彦君. G-S变换的快速算法[J]. 地球物理学报, 2000, 43(5): 684-690. [本文引用:1]
[19] 王华军. 正余弦变换的数值滤波算法[J]. 工程地球物理学报, 2004, 1(4): 329-333. [本文引用:2]
[20] 陈入云, 向淑晃. 一种正余弦变换的改进高效算法[J]. 工程地球物理学报, 2008, 5(4): 416-419. [本文引用:1]
[21] 徐振平, 胡文宝. 一种高精度瞬变电磁响应正演的数值滤波算法[J]. 石油物探, 2011, 50(03): 213-219. [本文引用:1]
[22] Raiche A P. Transient electromagnetic field computations for polygonal loops on layered earth[J]. Geophysics, 1987, 526: 785-793. [本文引用:1]
[23] Villinger H. Solving cylindrical geothermal problems using Gaver-Stehfest inverse Laplace transform[J]. Geophysics, 1985, 50(10): 1581-1587. [本文引用:1]
[24] 考夫曼A A, 凯勒 G V. 频率域和时间域电磁测深[M]. 北京: 地质出版社, 1987. [本文引用:1]
[25] 向淑晃. 一些高振荡积分、高振荡积分方程的高性能计算[J]. 中国科学: 数学, 2012, 42(7): 651-670, doi: DOI:10.3969/j.issn.1000-1441.2011.03.001. [本文引用:1]
[26] 朴化荣, 殷长春. 利用G-S逆拉氏变换法计算瞬变测深正演问题[J]. 物探化探计算技术, 1987, 9(4): 297-302. [本文引用:1]
[27] 罗回国. 瞬变电磁大定源回线一维正演模拟研究[D]. 北京: 中国地质大学, 2012. [本文引用:1]
[28] 牛之琏. 时间域电磁法原理[M]. 长沙: 中南大学出版社, 2007. [本文引用:2]
[29] 郭嵩巍. 中心回线瞬变电磁一维正反演算法研究[D]. 成都: 成都理工大学, 2010. [本文引用:1]
[30] 唐宝山. 瞬变电磁法中心回线装置一维正反演研究[D]. 北京: 中国地质大学, 2008. [本文引用:1]
[31] 华军, 蒋延生, 汪文秉. 双重贝塞尔函数积分的数值计算[J]. 煤田地质与勘探, 2001, 29(3): 58-61. [本文引用:1]
[32] Johansen H K, Sorensen K. Fast Hankel transforms[J]. Geophysical Prospecting, 1979, 27: 876-901. [本文引用:1]
[33] 李星. 瞬变电磁响应正反演及其特殊问题研究[D]. 成都: 成都理工大学, 2013. [本文引用:1]
[34] 李建慧, 朱自强, 刘树才, 等. 基于Gaver-Stehfest算法的矩形发射回线激发的瞬变电磁场[J]. 石油地球物理勘探, 2011, 46(3): 489-492. [本文引用:1]