引用本文
马振元, 杜文凤, 卢勇旭, 林朋. 基于最小平方滤波的面波压制方法[J]. 物探与化探, 2016,40(3): 561-567.
MA Zhen-Yuan, DU Wen-Feng, LU Yong-Xu, LIN Peng. A method based on least-squares filter of seismic ground-roll suppression[J]. Geophysical and Geochemical Exploration, 2016,40(3): 561-567.
Doi:10.11720/wtyht.2016.3.19  
Permissions
Copyright©2016, 《物探与化探》编辑部
《物探与化探》编辑部 所有
基于最小平方滤波的面波压制方法
马振元1,2, 杜文凤1, 卢勇旭1, 林朋1,2
1. 中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083
2. 中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083

作者简介: 马振元(1990-),男,在读硕士研究生,研究方向为地震数据处理。

收稿日期: 2015-08-07
基金: 国家自然基金煤炭联合项目(U1261203); 国家重大科学仪器设备开发专项(2012YQ030126)
摘要

在地震勘探中,强振幅、低频率的面波对于后续地震资料的处理和解释会产生重要影响。基于最小平方滤波的面波压制方法是一种新的面波压制方法,它与一般的频率域滤波方法不同。该方法的主要原理是利用扫描信号与滤波因子的褶积来预测面波,其中滤波因子的求取需要建立一个目标泛函。当目标泛函取得最小值时可从地震数据中求取滤波因子进而预测出面波,再将预测出的面波作为输入进行第二次面波预测,从地震记录中减去提取的面波,就得到去除面波后的地震数据。采用非线性的扫描信号提取面波,并对扫描信号起止频率进行了分析;通过对合成地震记录与煤田实际地震资料的处理,充分证明该方法能有效地压制面波。

关键词: 面波压制; 扫描信号; 滤波因子; 褶积; 最小平方滤波
中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)03-0561-07 doi: 10.11720/wtyht.2016.3.19
A method based on least-squares filter of seismic ground-roll suppression
MA Zhen-Yuan1,2, DU Wen-Feng1, LU Yong-Xu1, LIN Peng1,2
1. State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology(Beijing),Beijing 100083,China
2.College of Geosciences and Surveying Engineering, China University of Mining and Technology(Beijing),Beijing 100083,China
Abstract

In land seismic survey, the seismic data are mostly contaminated by ground-roll, which reduces the signal-to-noise ratio and impacts the quality of the seismic data seriously. The least-squares filter is a new means to suppress ground-roll, which is different from normal domain filter. The main principle of the method is the utilization of the convolution of scanning signal and filtering factor to predict ground-roll. It is necessary to construct the objective function to calculate the filter factor. The objective function is the least-squares error of seismic data and ground-roll. In that way, the targeting functionally obtained minimum can calculate filter factors from seismic data. The last step is to continue the second ground-roll suppression by making the extracted ground-roll as the input, which can get the seismic data and wipe out the ground-roll. In this paper, nonlinear sweep signal was used to extract ground-roll, and the sweep signal's beginning-ending frequency was analyzed. The results prove that the proposed method can effectively suppress the surface wave through synthesis of field data.

Keyword: ground-roll suppression; sweep signal; filter factor; convolution; least-squares filter

面波是地震勘探中的一种规则干扰波, 会大大降低地震资料的信噪比影响地震勘探精度。压制面波提高地震资料的信噪比, 对于后续地震资料的解释具有重要意义。根据面波的特性, 人们已经提出了许多压制面波的方法, 如高通滤波、F-K滤波[1]、f-x域去噪[2]、小波变换 36、Curvelet变换 78、S变换 912等。这些方法在压制面波方面都取得了一定的效果, 但也有其局限性。如高通滤波在压制面波时会严重损伤低频的有效信号; F-K滤波只适用于地层倾角平缓的情况, 对于复杂地区的面波压制效果不理想, 且容易产生假频或者混波现象; 由于面波呈现扫帚状, 小波变换在做面波线性时移时不能有效地对齐, 也不能很好地去除面波; S变换继承和发展了短时傅里叶变换和小波变换的思想, 能灵活地选择去除面波的时窗, 但它忽略了道与道之间的相关性而且针对多炮多道记录达不到预期的效果[13]。基于最小平方滤波的面波压制方法能够有效地压制面波而且对于有效波的损伤较小, 并在煤田地震资料测试中取得了较好的效果。

1 原理

基于最小平方滤波的面波压制方法的思想是先设计一个扫描信号, 然后与从地震数据中提取的滤波因子进行褶积运算来预测面波, 再从地震数据中去除预测出的面波, 达到压制面波的目的。滤波因子的求取是该方法的关键, 而求取滤波因子需要建立一个目标泛函F, 该目标函数是预测出的面波N与地震数据Z的误差能量。当F取得最小值时, 面波就能得到完全压制, 就可从地震数据中求出滤波因子进而预测出地震面波, 实现面波压制。

地震数据可看成由有效波与噪声两部分组成:

Zt=xt+nt, 　t=0, …, T1

其中:Zt为地震数据, xt为反射波, nt为噪声(这里特指面波)。

利用维纳滤波器设计一个面波信号来代替噪声nt。首先定义一个频率随时间变化的扫描信号[14]

st=sin[2πF(t)t]0≤t≤T0t< 0, t> T2

式中F(t)是确定扫描信号特性的函数, 最为常用的有线性和非线性两种:

F(t)=fb+fe-fb2Tt, (3)F(t)=fb+fe-fb2T)NtN。(4)

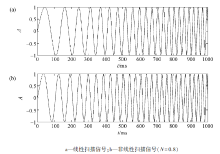
式(3)对应线性扫描信号, 式(4)对应非线性扫描信号; N是一个重要的参数, 它对扫描信号的特性有重要影响; fb为扫描信号的起始频率, fe为扫描信号的终止频率。扫描信号的波形图见图1。图1中两种类型的扫描信号采用的起止频率相同, 起始频率为5 Hz, 终止频率为45 Hz, 非线性扫描信号的N为0.8。

图1 扫描信号

然后设定一个滤波因子fτ , 将滤波因子与扫描信号进行褶积运算就可以将扫描信号转化为要求取的噪声信号nt, 即面波。滤波因子与扫描信号褶积运算前应先调整扫描信号的振幅和相位, 使其尽量和面波的相位、振幅相匹配。

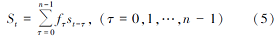
St是通过褶积运算得到的噪声, n为滤波因子的个数。滤波因子需要从地震数据中提取, 求取滤波因子fτ 就需要定义一个最小平方误差函数L:

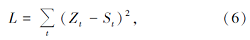
当L取得最小值时就可得到最佳滤波因子, 进而可以预测出精确的面波。将式(5)代入式(6)式得

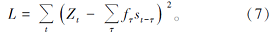
对L求导并令导数为零, 展开并化简得

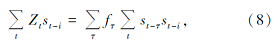
将其简化可得到

式(9)中, C为地震数据与扫描信号的互相关, R为扫描信号的自相关, 式(9)可写成矩阵形式

R0R1…Rn-1R1R0…R0⋮⋱⋮Rn-1Rn-2…R0f1f1⋮fn-1=C0C1⋮Cn-110

上式中矩阵R称为Toeplitz矩阵[15], 式(10)为Toeplitz方程组的矩阵形式。利用Levinson递推算法求解式(10)即可得到滤波因子fτ 。

将fτ 代入式(5)即可预测出面波St。最后将得到的St从地震数据中减去就得到有效反射波的数据yt:

yt=Zt-St。(12)

以上过程称为第一次面波压制。此时得到的地震数据虽然压制了大部分的面波, 但是有效波也有损伤。为了减少有效波的损伤, 以St作为原始的地震记录, 再次按照以上的流程操作进行第二次面波压制。此时获得提取的面波为Stt, 令Stt与St做差得到第一次面波压制损伤的有效反射波dt。最后就可得到最终的面波压制后的数据

Yt=yt+dt。(13)

在进行面波压制前一个重要步骤就是对地震数据进行振幅谱分析, 给定一个面波与反射波的频率参考范围, 便于确定扫描信号的起止频率。该方法进行面波压制时需要逐道进行操作。

2 理论模型测试

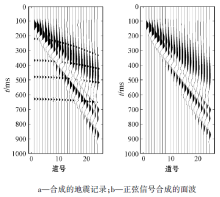
图2a是合成的单炮地震记录, 共24道接收, 时长为1 s。合成的地震记录中只包含有效反射波和面波, 地震子波采用主频为35~40 Hz的雷克子波, 面波的频率为5~15 Hz(见图2b)。从合成的地震记录中可以看到有效反射波被低频的面波所淹没。

图2 合成地震记录

2.1 面波压制效果

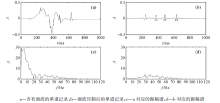
对模型处理采用非线性扫描信号, 起始频率为5 Hz, 终止频率为45 Hz, 参数N为0.8。利用基于最小平方滤波的面波压制方法对每一道地震记录进行处理, 提取滤波因子进而与扫描信号进行褶积运算提取面波。对合成的地震记录进行单道振幅谱分析, 图3a和3b分别为合成地震记录第十道处理前后的波形, 图3c、d分别为图3a、b对应的振幅谱; 从单道分析中可以看出低频的面波得到有效压制。对整个合成记录进行两次面波压制的效果见图4, 可以看出第二次面波压制的效果明显比第一次的效果好。前后两次的面波压制, 所采用扫描信号的起止频率不同, 相对于图4b而言, 图4c的同相轴质量得到明显的改善, 同时面波也得到有效的压制。说明采用不同的起止频率会对压制效果产生较大的影响。面波压制前后单道地震记录的有效波对比见图5, 从中可以看出该方法对有效波的损伤较小, 主要是由子波旁瓣引起的误差。

图3 单道振幅谱分析

图4 采用非线性扫描信号的面波压制效果

图5 处理前后有效反射波对比

2.2 扫描信号起止频率对面波压制效果的影响

由于扫描信号的起止频率是面波压制效果的重要影响因素, 如何合理地选取扫描信号的起止频率就成为关键问题, 这里以非线性的扫描信号为例进行研究。

1)起始频率fb。图6中a、b、c、d采用的起始频率分别为1、6、14、20 Hz, 终止频率采用固定的40 Hz。从图6a中可知采用起始频率较低时容易产生假频; 而随着起始频率的升高, 面波不能得到完全压制, 且面波压制的效果越来越差; 在起始频率取值为6~14 Hz时面波压制效果比较理想, 而且这一频率范围与面波频率范围相近。

2)终止频率fe。图7中a、b、c、d采用的终止频率分别为15、30、45、60 Hz。在起始频率为固定的7 Hz的情况下, 终止频率较低时会产生大量假频(图7a); 采用的频率较高时会对有效反射波造成损伤, 且频率越高有效反射波的损伤越大, 造成反射波同相轴模糊(图7d), 会降低地震数据的信噪比和分辨率; 终止频率的取值在30~45 Hz时面波得到了有效的压制, 而且这一频率范围与合成地震记录的有效反射波频率相近。

图6 起始频率的影响

图7 终止频率的影响

综上可知, 采用不同的起止频率, 面波压制的效果会产生较大差异, 因此起止频率的选择十分重要, 它除了与采样频率有关, 还与扫描信号的特性函数F(t)有关。从以上测试可得到:在采用非线性扫描信号的情况下, 起始频率与面波的频率相近且终止频率与有效反射波的频率相近时, 面波压制的效果最好。

3 实际资料测试

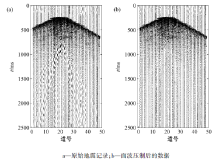
采用某煤田三维地震勘探的野外地震记录对该方法进行测试。野外地震记录的采样时长为 2 500 ms, 道间距为25 m。该地区的煤层埋藏较深, 在地震记录中位于750~800 ms之间。从图8a中可见煤层反射波受到面波的严重干扰, 这大大降低了地震资料的信噪比。对于实际地震资料测试, 首先采用扫描信号从地震数据中求取滤波因子, 让滤波因子与扫描信号进行褶积提取面波, 再进行第二次面波压制。用本文的方法对该煤田资料处理后的结果见图8b, 可以看出面波得到有效压制。

图8 野外实际地震资料面波压制

图9 提取的面波

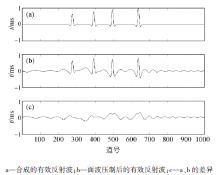
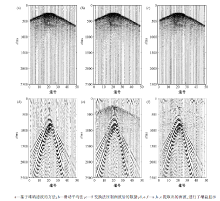
对实际地震记录进行频谱分析, 获取面波的大致频率范围。对实际地震数据进行面波压制采用的是非线性的扫描信号, 且扫描信号未加窗函数。扫描信号特性函数F(t)中参数N取值为0.7, 第一次提取面波时的起始频率采用5 Hz, 终止频率采用40 Hz。第二次采用的起始频率采用5 Hz, 终止频率采用30 Hz。经过两次面波压制分别提取的面波见图9, 第一次面波压制所提取的面波中包含了部分有效波, 并且产生了假频(图9a矩形框内); 第二次面波压制所提取的面波中基本上不再含有有效反射波, 而且第一次产生的假频也得到去除。第二次面波压制后, 会把损伤的有效反射波进行还原, 两次提取面波的差异为第一次面波压制时所损伤的有效反射波(图9c)。这说明了该方法在实际地震资料中能够有效地压制面波。

图10为采用不同方法的面波压制效果对比。可以看出本文的方法(对应于图10a、d)在压制面波和保护有效反射波方面具有明显的优越性, 而滑动平均方法(对应于图10b、e)和S变换方法(对应于图10c、f)虽然能有效地压制面波, 但在保护有效波方面有些不足。

图10 不同方法效果对比

4 结论

1) 扫描信号的起止频率对于面波压制的效果会产生很大的影响, 采用非线性扫描信号的情况下, 起始频率的取值与面波频率相近且终止频率的取值与有效反射波的频率相近时面波的压制效果最好。

2) 采用基于最小平方滤波的面波压制方法只进行一次面波压制的效果不理想, 会造成有效反射波损伤。经过两次面波压制能很好的将损伤的有效反射波恢复且将第一次面波压制中产生的假频去除。

3) 相比于其它面波压制方法, 基于最小平方滤波的面波压制方法能有效地压制面波且基本不损伤有效反射波, 具有较高的“ 保幅性” 。但是面波与有效波的频率相近的情况下, 该方法压制面波的效果就不太理想, 有待进一步改进。

The authors have declared that no competing interests exist.

参考文献
[1] 万光南. f-k滤波在压制面波噪声中的应用[J]. 中州煤炭, 2014, 2: 99-101. [本文引用:1]
[2] Ma Y Y, Li G F, Wang Y J, et al. Rand om noise attenuation by f-x spatial projection-based complex empirical mode decomposition predictive filtering[J]. Applied Geophysics, 2015, 12(1): 47-54. [本文引用:1]
[3] 曾祥堃, 乔宝平, 刘依谋, 等. 基于小波变换的自适应面波压制方法[J]. 北京大学学报: 自然科学版, 2015, 51(5): 837-842. [本文引用:1]
[4] 王超, 沈斐敏. 小波变换在探地雷达弱信号去噪中的研究[J]. 物探与化探, 2015, 39(2): 421-424. [本文引用:1]
[5] 林丹丹, 熊章强, 张大洲. 基于多模式分离的S变换与小波变换提取面波频散曲线对比分析[J]. 物探与化探, 2014, 38(3): 544-551. [本文引用:1]
[6] 陈文超, 高静怀, 包乾宗. 基于连续小波变换的自适应面波压制方法[J]. 地球物理学报, 2009, 52(11): 2854-2861. [本文引用:1]
[7] 董烈乾, 李振春, 王德营, 等. 第二代Curvelet变换压制面波方法[J]. 石油地球物理勘探, 2011, 46(6): 897-904. [本文引用:1]
[8] 韩佳君. Curvelet变换组合法压制地震随机噪声研究[D]. 长春: 吉林大学, 2010. [本文引用:1]
[9] 胡昊, 童思友, 龙江平. 基于GPU的时间S变换对面波的压制[J]. 地球物理学进展, 2014, 29(6): 2649-2656. [本文引用:1]
[10] 张大洲, 练小聪, 杨威, 等. 基于多模式分离的S变换瑞雷波频散曲线提取[J]. 中南大学学报: 自然科学版, 2015, 46(8): 2950-2956. [本文引用:1]
[11] 周竹生, 刘冰. 基于含可变因子S变换的面波压制技术[J]. 物探化探计算技术, 2013, 35(5): 555-560. [本文引用:1]
[12] 马见青, 李庆春, 王美丁. 广义S变换在地震勘探中的研究进展[J]. 物探与化探, 2011, 35(2): 265-269. [本文引用:1]
[13] 万学娟. 非理想条件下地震面波的性质及压制方法研究[D]. 青岛: 中国石油大学(华东), 2009. [本文引用:1]
[14] 郑恭明, 张海, 雷雪梅, 等. 基于片上可编程系统的可控震源扫描信号研究与设计[J]. 物探与化探, 2012, 36(3): 490-495. [本文引用:1]
[15] 梅金顺, 王润秋. Toeplitz矩阵循环延拓后的特征值数值分析[J]. 地球物理学进展, 2013, 28(1): 265-269. [本文引用:1]