引用本文
刘世宝, 陈鑫, 国显正, 王会敏, 郑有业, 许荣科, 王红军. 分形(多重分形)在区域化探数据处理中的应用——以柴北缘荒漠戈壁景观区为例[J]. 物探与化探, 2016,40(3): 550-556.
LIU Shi-Bao, CHEN Xin, GUO Xian-Zheng, WANG Hui-Min, ZHENG You-Ye, XU Rong-Ke, WANG Hong-Jun. Fractal/multifractal modeling of geochemical exploration data in desert landscape area of Qaidam Basin[J]. Geophysical and Geochemical Exploration, 2016,40(3): 550-556.
Doi:10.11720/wtyht.2016.3.17  
Permissions
Copyright©2016, 《物探与化探》编辑部
《物探与化探》编辑部 所有
分形(多重分形)在区域化探数据处理中的应用——以柴北缘荒漠戈壁景观区为例
刘世宝1, 陈鑫2, 国显正3, 王会敏2, 郑有业2,3, 许荣科3, 王红军2
1.青海省地质调查局,青海 西宁 810001
2.中国地质大学(武汉) 资源学院,湖北 武汉 430074
3.中国地质大学(武汉) 地质调查研究院,湖北 武汉 430074
通讯作者: 郑有业(1962-),男,教授,博士生导师,主要从事基础地质、成矿规律及矿产勘查评价工作。E-mail:zhyouye@163.com

作者简介: 刘世宝(1965-),男,高级工程师,主要从事地质矿产勘查工作。E-mail: 843594591@qq.com

收稿日期: 2015-05-07
基金: 中国地质调查局项目(1212011121204)
摘要

通过搜集柴北缘1∶20万区域地球化学数据,运用分形(多重分形)方法来确定荒漠戈壁景观区受风成沙影响的地球化学异常特征,并利用C-A和S-A模型分别探讨了景观地区Au的地球化学异常特征。研究表明,C-A模型在确定异常下限时有优势,但也存在局限性;S-A模型能够很好地排除背景场和干扰因素,缩小异常面积,突出弱小异常。基于该方法提取的异常元素区域能够较好地识别出绝大多数已知矿床,同时指示了值得作进一步异常查证的空白成矿元素异常区域,为勘查工作提供参考,值得开展下一步的找矿工作。

关键词: 分形(多重分形); 荒漠戈壁景观区; 地球化学异常; 成矿元素; 异常区域
中图分类号:P632 文献标志码:A 文章编号:1000-8918(2016)03-0550-07 doi: 10.11720/wtyht.2016.3.17
Fractal/multifractal modeling of geochemical exploration data in desert landscape area of Qaidam Basin
LIU Shi-Bao1, CHEN Xin2, GUO Xian-Zheng3, WANG Hui-Min2, ZHENG You-Ye2,3, XU Rong-Ke3, WANG Hong-Jun2
1. Qinghai Geological Survey, Xining 810001,China
2. Faculty of Earth Resources, China University of Geosciences, Wuhan 430074, China
3. Institute of Geological Survey, China University of Geosciences, Wuhan 430074,China
Abstract

On the basis of previous work, the authors collected 1∶200 000 regional geochemical data along the northern margin of Qaidam Basin,used fractal (multifractal) method to determine geochemical anomaly characteristics in Gobi desert area of eolian sand, and adopted the C-A and S-A model to investigate the characteristics of geochemical anomaly of Au element influenced by eolian sand in the Gobi desert area. The results show that C-A model has advantages in determining the threshold but still has some limitations. S-A model can well eliminate the background field and interference factors, reduce the area of anomaly, and can make prominent the small weak anomaly. The method of extracting the region of anomalous elements can be used to identify the vast majority of known ore deposits and indicate the further anomal anomaly area of ore-forming elements based on the geochemical data, thus providing a reference for further exploration.

Keyword: fractal (multifractal); Gobi desert landscape area; geochemical anomaly characteristics; metallogenic elements; anomaly region

中图分类号: P632 文献标识码: A 文章编号: 1000-8918(2016)03-0550-07

分形(多重分形)模型在勘查地球化学领域是一个很有吸引力的研究课题, 对识别和确定地球化学异常是一个强有力的工具 16。为了更好地对地球化学异常进行圈定、筛选、评价和靶区验证工作, 成秋明等提出的利用分形与多重分形技术进行元素地球化学分析, 逐渐成为目前研究地球化学规律的重要途径[7, 8]。许多学者也应用分形(多重分形)模型来研究地球化学数据, 并对其进行了有意义的探讨 924。申维应用分形求和法来确定地球化学数据分组界限, 有效确定了澳大利亚新南威尔士东北地区水系沉积物中Cu的异常下限[25]; 谢淑云等分别将C-A分形模型和抛物线分形方法应用于西藏东部某矿区外围水系沉积物地球化学异常的圈定与成矿潜力评价中[26]; Peyman Afzal等将S-A多重分形方法应用于伊朗中部Kahang斑岩型Cu-Mo矿成矿地区, 其结果指出S-A法在化探与矿产勘查工作中具有好的应用潜力[27]; 夏庆霖等在外蒙古的草原覆盖区使用C-A和S-A模型研究地球化学异常, 认为S-A模型在草原覆盖区能够很好地确定异常, 但是其产生的边缘效应值得注意[28]; 左仁广等在南方植被覆盖区使用S-A模型研究福建的水系沉积物样品, 确定了热液型Pb、Zn、Au、Cu多金属地球化学异常[4], 并在中国北部盖层很厚的草原覆盖区潮不冷铁矿进行了实验, 发现C-A模型在寻找弱的地球化学信息时有一定的局限性, S-A模型能够增强盖层很厚的草原覆盖区低地球化学背景中的小弱异常 2931。

笔者以受风成沙严重影响的戈壁荒漠景观— — 柴北缘地区为例, 研究区域地球化学数据特征, 通过分形(多重分形)模型探讨荒漠戈壁地区地球化学异常的识别。与常规化探处理方法结果显示不同, 分形(多重分形)方法圈定的异常与已知矿点(矿化点)基本重合, 具有重要的理论意义和找矿意义, 同时指示了值得作进一步异常查证的空白成矿元素异常区域。

1 研究区概况

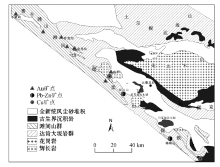
研究区位于赛什腾— 绿梁山— 锡铁山形成的柴北缘缝合带, 以北位于欧龙布鲁克微陆块, 以南为柴达木陆块[32] (图1)。研究区出露的地层主要为滩间山群、达肯大坂岩群和中新生界地层[33]。滩间山群为一套以基性、中基性为主的火山岩, 并有沉积碎屑岩, 偶见大理岩建造; 达肯大坂岩群主要为一套变质程度较浅的变质岩, 可分为斜长角闪岩组和变质碎屑岩组; 少量的鱼卡河沿群主要为一套经历榴辉岩相变质的超高压变质岩[34]; 中新生界地层主要为城墙沟组、油砂沟组和第四系沉积物。区内岩浆岩发育, 从古生代到中生代岩浆活动频繁, 东部有大面积的花岗岩出露。研究区内矿床比较发育, 在古元古界达肯达坂岩群中有与混合岩化作用有关的白云母、绿柱石等伟晶岩型矿床, 海相火山岩型铁矿在寒武— 奥陶系的不同层位中产出, 酸性火山岩建造相对发育的地段有利于多金属、金和钴等矿床的形成。例如已发现的著名锡铁山铅锌矿, 石炭系为陆棚浅海相夹滨海相的碎屑岩和碳酸盐岩沉积, 生成滨海相煤层, 陆相侏罗纪河湖— 湖沼型沉积盆地广泛分布, 其中的早、中侏罗世是湖沼发育时期, 普遍沉积了含煤碎屑岩地层、工业煤层以及钾盐类等矿床。

图1 柴北缘区域地质简要(据参考文献[35]修改)

2 区域地球化学特征

对柴北缘地区1∶ 20万区域化探数据进行统计, 得到化探数据3 335个。野外按4 km× 4 km布设测网, 采样面积约6.69万km2。柴北缘地区荒漠化严重, 少量受风成沙影响严重的地段没有进行采样。对区域元素数据进行统计分析, 可以看出(表1), 研究区主成矿元素变异系数基本都大于1, 只有Co、Hg接近1, 说明该地区元素地球化学活动性很强, 区域分布很不均匀。Ni、Cr、Co富集系数相对较高, 可能与滩间山群的超基性、基性火山岩密切相关。与造山型和块状硫化物矿床相关的主成矿元素Au、Zn、Cu、Pb的富集系数反而低于地壳丰度, 说明这些元素很可能出现了局部富集的情况。

表1 柴北缘地区地球化学元素统计特征值

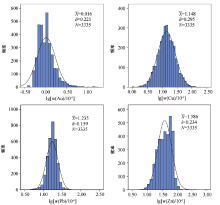
为了更好地验证研究区主成矿元素特征, 对主成矿元素的频率分布进行统计(图2)。Au、Zn、Cu、Pb呈近似正态分布, 其中Cu正态分布效果最好, Pb、Zn左偏, Au右偏, 说明主成矿元素在空间分布上并不完全服从中心极限定理, 元素的分散富集在空间上有一定的奇异性[36]。在对原始数据作对数变换后, 经过3次特高值和特低值剔除替换, 使得数据基本服从对数正态分布, 并计算出各地球化学参数数值。根据T=X+kS计算异常下限, 其中X为平均值, S为标准方差[37]。本次K取值为2, 结合区域地球化学特征对异常下限进行了微调, 计算得到Au的异常下限为2.2× 10-9, 取值为2.00× 10-9; Cu异常下限为53.7× 10-6, 取值为50.00× 10-6; Pb异常下限为27.72× 10-6, 取值为27× 10-6; Zn异常下限79.56× 10-6, 取值为79× 10-6。使用MapGIS 6.7软件对数据进行网格化, 网格间距为10 km, 得到Zn、Cu、Pb、Au的含量等值线图(图3)。研究区已经发现的金属矿床主要位于滩间山群, 其中滩间山金矿、锡铁山铅锌矿等大型矿床都产在与火山岩相关的滩间山群中(图1), 元素异常高值都是沿着柴北缘缝合带呈线性分布。在东部大面积花岗岩出露的地区出现了强烈的Zn、Cu、Pb、Au负异常。

图2 柴北缘地区部分元素地球化学数据正态分布

图3 柴北缘地区Au、Cu、Pb、Zn地球化学分布

3 分形模型的应用与探讨
3.1 C-A模型

为了更好地研究荒漠戈壁景观区元素地球化学行为, 采用分形(C-A)和多重分形(S-A)的方法, 对该地区的Au地球化学异常进行圈定, 探讨不同方法的应用效果。

成秋明教授在1994提出了C-A模型[1, 25, 39, 40], 开创了分形领域里处理化探数据的先河[41], 该方法也成为了在确定异常下限中比较有效的方法。模型中, c代表元素含量大小的度量, A 代表元素含量频率的度量。以此为基础提出了“ 含量— 面积” 方法, 用面积代替频率, 使频率有了空间位置, 从而使分形更好地服务于预测。具体含义是:地球化学元素含量密度高于c时的面积A与c服从幂指数关系, 即A与c服从分形关系[6]。C-A模型可以度量密度与面积的各向异性, 因此不同斜率线段所对应的分界值就可以作为区分背景和异常的临界值。C-A模型可以表示为[42]:

A≧c)=kc-D,

两边以10为底取对数得:lgA(≧ c)=lgk-Dlgc。

式中A(≧ c)表示元素含量大于c的区域面积; D 为分维数, 反映的是A随c变化的规律; k为比例常数。该模型定量刻划了地球化学元素分布的变化程度。lgA(≧ c)和lgc服从一次函数, 分维数(斜率)D的估计量可以用最小二乘法求出, 采用分段拟合[43]。

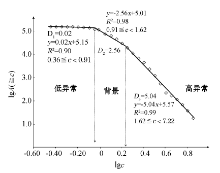
对柴北缘地区的Au数据在MapGIS 6.7软件数字地面模型子系统中使用克里格进行网格化处理[44], 对其含量和面积在MapGIS 6.7空间分析中进行统计, 可以看出, Au含量在一定浓度区间段内服从分形分布, 使用最小二乘法可以分为三段(图4), 每段的R2都不小于0.90。通过回归性检验, 左边弱异常回归方程为y=-0.02x+5.15(0.36≦ c< 0.91), 分位数D1=0.02; 中间背景回归方程为y=-2.56x+5.01(0.91≦ c< 1.62), 分位数D2=2.56; 右边强异常回归方程为y=-5.04x+5.57(1.62≦ c< 7.22), 分位数D3=5.04。通过联立右边强异常回归方程和中间背景回归方程, 可以得出异常对数值为0.21, 真值为1.62× 10-9, 小于常规地球化学方法得到的异常下限值2.20× 10-9。存在差别的原因可能是传统方法确定的异常下限对特高值进行了剔除, 存在很大的人为因素, 而C-A模型不要求对数据进行任何处理。由此得出了对应的Au异常图(图5a), 已发现的矿(化)点都在异常范围之内。

图4 柴北缘Au的C-A模型(lg A(≧ c)-lgc)双对数

图5 C-A模型、S-A模型下Au异常分布及成矿远景预测

但该方法也存在不足:在确定异常下限时存在局限性, 统一异常下限, 将背景当成平面来处理, 与常规地球化学处理方法相比不占优势, 虽然与已知矿(化)点相吻合, 但是异常面积大, 给异常筛选、评价和靶区验证工作带来困难。

3.2 S-A模型

进一步将 C-A 模型推广到频率域, 成秋明建立了多重分形场的“ 能谱密度— 面积” 分形模型[7, 31, 41, 43, 45]。物化探异常不仅可以具有形式的多样性(如异常强度、大小范围、不同背景等), 而且在频率域中具有与背景场表现不同的自相似性。这种自相似性可以由幂率模型所刻画[46]:

A(S≧s)=KS-2d/s, 取对数得lnA(S≧s)=lnK-2d/slnS。

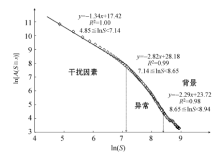
其中, A(S≧ s)表示能谱密度S大于某一值s的区域面积, 2d/s为指数。不论化探异常的强度、形态以及所处的背景是否相同, 如果它们具有内在的相似性, 在能谱密度空间中就可能呈现广义自相似性, 而且与背景场所表现的自相似性是不同的, 随着S值的增高, A总是相应的减小。该方法主要是基于成秋明等开发的GeoDAS上进行[47], 使用多重反距离插值方法(MIDW)得到研究区Au栅格图像[28]; 使用正傅里叶变换将空间栅格数据从空间域转化到频谱域, 对能谱密度(S)和大于该密度的面积进行双对数处理, 使用最小二乘法拟合出了三段方程(图6), 每段R2都大于0.98, 拟合效果非常显著。GeoDAS中共有三种滤波器, 即异常滤波器(GA)、背景滤波器(GB)和带通滤波器(GC)[22]。这种滤波技术可以去掉其他的干扰因素, 保留想要得到的其他因素[31]。从图6拟合的双对数曲线中可以看出, 最左边的线(y=-1.34x+17.42, 4.85≦ lnS< 7.14)代表干扰因素, 中间的线(y=-2.82x+28.18, 7.14≦ lnS< 8.65)代表异常, 最右边的线(y=-2.29x+23.72, 8.65≦ lnS< 8.94)代表背景值[2, 28]。

图6 柴北缘Au的S-A模型双对数

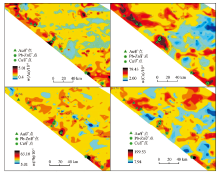
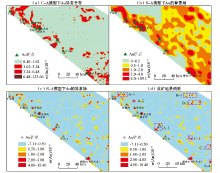
使用负傅里叶变换函数把频率域的分量重新转换到空间域中, 得到对应的背景图(图5b)和异常图(图5c)。从图中可以看出, 该方法能够克服高背景的影响, 从高背景中提取地球化学的致矿异常, 大柴旦滩间山青龙沟(大型)、大柴旦镇细金沟(小型)金矿都在异常图中处于高异常位置, 异常面积范围明显小于常规方法和C-A模型圈出的异常, 能够更好地进行异常的筛选和查证工作。大柴旦红柳沟、冷湖镇千枚岭等两个小型金矿在常规方法(X+2S)确定的异常图中几乎无异常, 但在S-A分解的异常图能够看到矿床位于异常中心的边缘地带, 具有很好的指示意义。从背景图中可以看出, Au的高背景地段主要分布在滩间山群和土尔根大坂山以北的地区, 这两个地区Au相对富集, 金矿形成的可能性明显高于其他地段。

4 异常远景区预测

基于S-A模型下的Au异常, 对研究区的成矿远景区进行圈定(图5d)。根据已知的矿床、矿点主要特征, Au矿点均分布在滩间山群, 其地层中金的背景值高, 成矿可能性最大, 在其周边圈定了4个A类成矿远景区:A-1、A-2、A-3、A-4, 笔者已经在A-3等地的异常中心发现了金矿化线索, 目前正在开展工作。达肯大坂岩群以北划分出B-1、B-2两个远景区, C-A模型和S-A模型下的异常都很显著, 但是该地区的找矿工作目前尚未取得很大突破, C-A模型下圈定的异常面积大, 很难进行异常查证, 而S-A模型能够很好地缩小异常靶区, 在该模型下圈定的B-1、B-2远景区有很大的成矿空间。C-1、C-2异常主要分布在达肯大坂岩群, 但是该区域离大岩体较近, 可能会受到岩体等的影响, 成矿可能性弱于B-1、B-2, 但其异常面积小, 值得开展异常查证工作。

5 讨论与结论

1)传统方法确定的Au异常下限为2.2× 10-9, 使用C-A模型确定的Au异常下限为1.62× 10-9, 存在差别的原因可能是传统方法对数据特高值进行了剔除, 存在很大的人为因素, 而C-A(含量— 面积)模型不要求对数据进行任何处理。

2)C-A模型虽然与已知矿(化)点吻合较好, 但是其圈定的异常面积大, 不利于对地球化学异常进行筛选和评价。

3)S-A(频率— 面积)模型在确定地球化学异常中有很大的优势, 背景场能够很好地发现含矿地层, 容易对地球化学数据进行分区处理; 异常场能够很好地排除背景场和干扰因素; 高异常场中能够缩小异常面积, 突出小弱异常, 在该地区有很好的应用效果, 能够为西北荒漠地区找矿工作提供参考。

4)基于S-A模型下的Au异常, 圈定了4个A类, 2个B类, 2个C类成矿远景区, 并且对A-3异常中心进行查证工作, 发现了金矿化点, 取得了较好的应用效果。

The authors have declared that no competing interests exist.

参考文献
[1] Cheng Q, Agterberg F P, Ballantyne S B. The separation of geochemical anomalies from background by fractal methods[J]. Journal of Geochemical Exploration, 1994, 51(2): 109-130. [本文引用:1]
[2] Zuo R. Identification of geochemical anomalies associated with mineralization in the Fanshan district, Fujian, China[J]. Journal of Geochemical Exploration, 2014, 139(1): 170-176. [本文引用:1]
[3] Nouri R. Correlation between Cu mineralization and major faults using multifractal modelling in the Tarom area (NW Iran)[J]. Geologica Carpathica, 2013, 64(5): 409-416. [本文引用:1]
[4] Zhao J, Chen S, Zuo R. Identifying geochemical anomalies associated with Au-Cu mineralization using multifractal and artificial neural network models in the Ningqiang district, Shaanxi, China[J]. Journal of Geochemical Exploration, 2015, 164: 54-64. [本文引用:1]
[5] Cheng Q, Xu Y, Grunsky E. Integrated Spatial and Spectrum Method for Geochemical Anomaly Separation[J]. Natural Resources Research, 2000, 9(1): 43-52. [本文引用:1]
[6] 张立. 基于核主成分分析和多重分形的地球化学综合异常信息提取[D]. 成都: 成都理工大学, 2014. [本文引用:1]
[7] Zuo R, Carranza E J M, Cheng Q. Fractal/multifractal modelling of geochemical exploration data[J]. Journal of Geochemical Exploration, 2012, 122(1): 1-3. [本文引用:2]
[8] Zuo R, Xia Q, Zhang D. A comparison study of the C-A and S-A models with singularity analysis to identify geochemical anomalies in covered areas[J]. Applied Geochemistry, 2013, 33(6): 165-172. [本文引用:1]
[9] 陈永清, 张生元, 夏庆霖, 等. 应用多重分形滤波技术提取致矿地球化学异常: 以西南“三江”南段Cu、Zn致矿异常提取为例[J]. 地球科学, 2006, 31(6): :861-866. [本文引用:1]
[10] 成秋明. 应用复杂性—非线性理论开展成矿预测——奇异性理论—广义自相似性—分形谱系多重分形理论与应用[C]//第八届全国矿床会议, 2006: 463-466. [本文引用:1]
[11] 申维. 分形不变分布及其在山东地区金矿床中的应用[J]. 地学前缘, 2008, 15(4): 65-70. [本文引用:1]
[12] 谢淑云, 鲍征宇. 多重分形与地球化学元素的分布规律[J]. 地质地球化学, 2003, 31(3): 97-102. [本文引用:1]
[13] 成秋明. 多维分形理论和地球化学元素分布规律[J]. 地球科学: 中国地质大学学报, 2000, 25(3): 311-318. [本文引用:1]
[14] 李晓晖, 袁峰, 贾蔡, 等. 基于多维分形模型与指示克里格方法的地球化学异常识别研究[J]. 地理与地理信息科学, 2011, 27(6): 23-27. [本文引用:1]
[15] Zuo R. Identification of weak geochemical anomalies using robust neighborhood statistics coupled with GIS in covered areas[J]. Journal of Geochemical Exploration, 2014, 136(1): 93-101. [本文引用:1]
[16] Zuo R, Wang J, Chen G, et al. Identification of weak anomalies: A multifractal perspective[J]. Journal of Geochemical Exploration, 2014, 154: 12-24. [本文引用:1]
[17] Zuo R. Identifying geochemical anomalies associated with Cu and Pb-Zn skarn mineralization using principal component analysis and spectrum-area fractal modeling in the Gangdese Belt, Tibet (China)[J]. Fuel & Energy Abstracts, 2011, 111(1): 13-22. [本文引用:1]
[18] 白晓宇, 袁峰, 周涛发, 等. 多重分形方法识别铜陵矿区土壤中Cd的地球化学异常[J]. 矿物岩石地球化学通报, 2008, 27(3): 306310 [本文引用:1]
[19] 柯贤忠, 谢淑云, 高顺宝, 等. 西藏班戈地区化探数据的多重分形特征及其成矿意义[J]. 地质科技情报, 2015, 34(1): 148-153. [本文引用:1]
[20] 陈建国, 王仁铎, 陈永清. 利用分形统计学提取化探数据中的隐蔽信息并圈定地球化学异常[J]. 地球科学: 中国地质大学学报, 1998, 23(2): 175-178. [本文引用:1]
[21] 成秋明, 赵鹏大, 陈建国, 等. 奇异性理论在个旧锡铜矿产资源预测中的应用: 成矿弱信息提取和复合信息分解[J]. 地球科学: 中国地质大学学报, 2009, 34(2): 232-242. [本文引用:1]
[22] 成秋明. 非线性成矿预测理论: 多重分形奇异性广义自相似性分形谱系模型与方法[J]. 地球科学: 中国地质大学学报, 2006, 31(3): 337348. [本文引用:1]
[23] 毛华海, 张哲儒. 分形理论与成矿作用[J]. 地学前缘, 2000, 7(1): 195-204. [本文引用:1]
[24] Asadi H H, Kianpouryan S, Lu Y, et al. Exploratory data analysis and C-A fractal model applied in mapping multi-element soil anomalies for drilling: A case study from the Sari Gunay epithermal gold deposit, NW Iran[J]. Journal of Geochemical Exploration, 2014, 145: 233-241. [本文引用:1]
[25] 张磊, 申维. 分形方法在澳大利亚新南威尔士地区地球化学异常下限确定中的应用[J]. 地质通报, 2009, 28(2): 245-249. [本文引用:2]
[26] Ke X, Xie S, Zheng Y, et al. Multifractal analysis of geochemical stream sediment data in Bange Region, northern Tibet[J]. Journal of Earth Science, 2015, 26(3): 317-327. [本文引用:1]
[27] Afzal P, Harati H, Fadakar Alghaland is Y, et al. Application of spectrum-area fractal model to identify of geochemical anomalies based on soil data in Kahang porphyry-type Cu deposit, Iran[J]. Chemie der Erde-Geochemistry, 2013, 73(4): 533-543. [本文引用:1]
[28] Zuo R, Xia Q, Zhang D. A comparison study of the C-A and S-A models with singularity analysis to identify geochemical anomalies in covered areas[J]. Applied Geochemistry, 2013, 33(6): 165-172. [本文引用:3]
[29] Zuo R, Cheng Q, Xia Q. Application of fractal models to characterization of vertical distribution of geochemical element concentration[J]. Journal of Geochemical Exploration, 2009, 102(1): 37-43. [本文引用:1]
[30] Zuo R, Cheng Q, Agterberg F P, et al. Application of singularity mapping technique to identify local anomalies using stream sediment geochemical data, a case study from Gangdese, Tibet, western China[J]. Journal of Geochemical Exploration, 2009, 101(3): 225-235. [本文引用:1]
[31] Zuo R. Decomposing of mixed pattern of arsenic using fractal model in Gangdese belt, Tibet, China[J]. Applied Geochemistry, 2011, 26(3): S271-S273. [本文引用:2]
[32] 查显锋, 辜平阳, 计文化, 等. 欧龙布鲁克地块西段达肯大坂岩群物质组成及变形特征研究[J]. 地质科学, 2013, 48(4): 1103-1114. [本文引用:1]
[33] 陈鑫, 郑有业, 许荣科, 等. 柴北缘超高压变质带折返过程对金红石成矿的制约: 来自鱼卡和铁石观西地区石榴石成分环带的证据[J]. 地球科学与环境学报, 2016, 38(2): 143-159. [本文引用:1]
[34] 陈鑫, 许荣科, 郑有业, 等. 青海柴北缘UHP变质带铁石观西榴辉岩峰期温度的确定及其地质意义[J]. 地质通报, 2015, 34(12): 2292-2301. [本文引用:1]
[35] 张雪亭. 青海省大地构造格架研究[D]. 北京: 中国地质大学, 2006. [本文引用:1]
[36] Cheng Q. Non-linear theory and power-law models for?Information integration and mineral resources quantitative assessments[J]. Mathematical Geosciences, 2008, 40(5): 503-532. [本文引用:1]
[37] 蒋敬业. 应用地球化学[M]. 武汉: 中国地质大学出版社有限责任公司, 2013. [本文引用:1]
[38] 黎彤. 中国陆壳及其沉积层和上陆壳的化学元素丰度[J]. 地球化学, 1994(2): 140-145. [本文引用:1]
[39] 姜振宁. 地球化学数据处理方法比较[D]. 石家庄: 石家庄经济学院, 2012. [本文引用:1]
[40] 赵江南, 陈守余, 左仁广. 个旧锡多金属矿集区高松矿田矿化元素局部富集的奇异性特征[J]. 吉林大学学报: 地球科学版, 2012(S1): 216-223. [本文引用:1]
[41] Zuo R. Exploring the effects of cell size in geochemical mapping[J]. Journal of Geochemical Exploration, 2012, 112(1): 357-367. [本文引用:2]
[42] 成秋明, 张生元, 左仁广, 等. 多重分形滤波方法和地球化学信息提取技术研究与进展[J]. 地学前缘, 2009, 16(2): 185-198. [本文引用:1]
[43] 陈永清, 张生元, 夏庆霖, 等. 应用多重分形滤波技术提取致矿地球化学异常: 以西南“三江”南段Cu、Zn致矿异常提取为例[J]. 地球科学: 中国地质大学学报, 2006, 31(6): 861-866. [本文引用:2]
[44] 李随民, 姚书振. 基于MAPGIS的分形方法确定化探异常[J]. 地球学报, 2005, 26(2): 187-190. [本文引用:1]
[45] Zuo R, Agterberg F P, Cheng Q, et al. Fractal characterization of the spatial distribution of geological point processes[J]. International Journal of Applied Earth Observation and Geoinformation, 2009, 11(6): 394402. [本文引用:1]
[46] Singer D A, Kouda R. Some simple guides to finding useful information in exploration geochemical data[J]. Natural Resources Research, 2001, 10(2): 137-147. [本文引用:1]
[47] Cheng Q. GeoData analysis system (GeoDAS) for mineral exploration: unpublished User‘s guide and exercise manual[C]//Material for the Training Workshop on GeoDAS, York University, 2000. [本文引用:1]