GRNN与LS-SVM方法在计算煤质工业组分中的应用

引用本文

周大鹏, 王祝文, 李晓春. GRNN与LS-SVM方法在计算煤质工业组分中的应用[J]. 物探与化探, 2016,40(1): 88-92.
ZHOU Da-Peng, WANG Zhu-Wen, LI Xiao-Chun. The application of GRNN and LS-SVM to coal properties calculation[J]. Geophysical and Geochemical Exploration, 2016,40(1): 88-92.
Doi:10.11720/wtyht.2016.1.16 复制到剪切板

Permissions

GRNN与LS-SVM方法在计算煤质工业组分中的应用

周大鹏¹, 王祝文¹, 李晓春²

1. 吉林大学地球探测科学与技术学院,吉林长春 130026

2. 内蒙古自治区煤田地质局,内蒙古呼和浩特 010000

通讯作者:王祝文(1961-),男,教授,博士生导师,主要从事地球物理测井新方法新技术以及复杂岩性的地球物理测井解释和评价、核地球物理、辐射与环境评价等方面的教学和科研工作。E-mail:wangzw@jlu.edu.cn

作者简介: 周大鹏(1992-),男,硕士研究生,研究方向为地球物理测井。

收稿日期: 2015-05-25

基金: 国家高技术研究发展计划(“863”计划)项目(2014AA06A609)

摘要

在煤炭开发过程中,对煤质的评价尤为重要。依靠实验室分析来确定煤质的工业组分效率比较低,成本也比较高,因此通过建立其与测井参数之间的关系来进行各组分的计算。选取自然伽马、双收时差、密度以及三侧向电阻率这四个测井参数为输入的特征参数,煤质的水分、灰分、挥发分以及固定碳的含量作为输出结果,利用在某煤田挑选的73层测井数据当作训练样本,构建了基于广义回归神经网络(GRNN)以及最小二乘支持向量机(LS-SVM)的计算模型,从而建立了测井参数与各工业组分之间的关系。对19层的测试数据进行了检验,结果表明这两种方法均能应用于实际的生产之中;相比之下,广义回归神经网络能更准确地计算出各组分的含量,其平均平方误差均在1%以下。

关键词: GRNN; LS-SVM; 煤田测井; 煤质工业组分; 自然伽马; 双收时差; 三侧向电阻率

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)01-0088-05 doi: 10.11720/wtyht.2016.1.16

The application of GRNN and LS-SVM to coal properties calculation

ZHOU Da-Peng¹, WANG Zhu-Wen¹, LI Xiao-Chun²

1. College of Geoexploration Science and Technology, Jilin University, Changchun 130026,China

2. Coal Geological Bureau of Inner Mongolia, Hohhot 010000, China

Abstract

As one of the most pivotal resources, coal cannot be replaced. The evaluation of coal properties plays an essential role in the development. The calculation of coal properties based on laboratory analysis is inefficient and expensive. In this paper, the authors have resolved this problem by establishing the relationship between logging parameters and coal properties. Natural gamma, time difference, density and three-lateral resistivity are treated as input, and values of moisture, ash, volatile matter and fixed carbon are chosen as output. By using 73-layer logging data to train, the authors constructed a model based on GRNN and LS-SVM to calculate coal qualities. Through testing 19-layer data, the authors have reached the conclusion that these two methods can be well used in practice. The GRNN can calculate the content of moisture, ash, volatile matter and fixed carbon more accurately than LS-SVM, with its mean square error lower than 1%.

Keyword: GRNN; LS-SVM; coalfield logging; coal qualities; natural gamma; time difference; three-lateral resistivity

Show Figures

虽然目前我国的能源结构已经有了很大的改善, 但煤炭作为国民经济发展的重要资源, 仍然有着举足轻重的作用, 各领域对煤炭资源的消耗量仍然很大, 只有做好资源开采和高效利用才能更好发挥煤炭资源的作用。在煤炭资源开发过程中, 煤质的工业评价是很重要的一个方面^[1]。目前, 煤质工业参数求取主要依靠取心分析, 这种方法工作效率低, 代价昂贵, 并且只能得到特定煤层的总体特征, 而不能进行煤层内部精细解释。建立测井参数与工业组分之间的关系可以很好地解决这一问题。

近来, 煤田测井无论是在仪器装备还是数据处理技术方面都得到了长足发展, 多年的测井工作实践证明煤质的工业组分与测井参数之间有着一定的关系^{[2, 3]}。但是常规解释模型的建立需要很多的假设条件, 并且解释模型的使用还受很多其他因素的限制。神经网络等学习算法适合解决存在某种潜在联系但又无法确切表达的问题, 在油气藏测井评价中已经得到广泛应用^{[4, 5, 6, 7]}。笔者借鉴油气藏中的测井评价方法, 探讨GRNN神经网络和LS-SVM在煤质工业分析中的应用。

1 GRNN神经网络概述

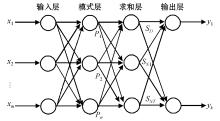
广义回归神经网络(Generalized Regression Neutral NetWork, GRNN)是美国学者Donald F. Specht 在1991年提出的一种径向基神经网络, 具有很强的非线性映射能力、高度的鲁棒性以及柔性网络结构, 适于解决非线性问题^[8]。GRNN与一般的网络相比有更好的逼近能力和更快的学习速度, 最后收敛于积聚样本量较多的回归面, 并且当样本数据比较少时, 预测效果也很好。在结构上, GRNN由四层组成, 如图1所示, 分别为输入层、模式层、求和层和输出层^[9]。对应网络输入X=[x₁, x₂, …, x_m]^T, 其输出为Y=[y₁, y₂, …, y_k]^T。

	Figure Option View Download New Window
	图1 广义回归网络结构

1) 输入层:各神经元是简单的分布单元, 输入层神经元的数目等于输入向量的维数, 直接将输入传递给模式层。

2) 模式层:模式层神经元的数目与样本的数目n一致, 各个神经元对应不同的样本, 神经元传递函数为

$\begin{matrix} P_{i} = \exp [- \frac{(X - X_{i})^{T} (X - X_{i})}{2 σ^{2}}] i = 1, 2, \dots, n 。 \end{matrix}$ (1)

神经元i的输出为输入变量与其对应样本之间Euclid距离平方的指数形式。其中X为输入变量; X_i为第i个神经元对应的学习样本。

3) 求和层:这种求和方法可以分为两类。一类为

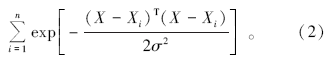
其对模式层所有神经元的输出进行算数求和, 模式层与神经元的连接权值为1, 其传递函数为

另一类计算公式为

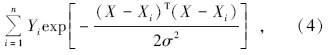
对模式层的神经元进行加权求和, 模式层中第i个神经元与求和层中第j个神经元之间的连接权值为第i个输出样本Y_i中的第j个元素, 传递函数为

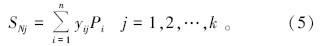
4) 输出层:输出层中神经元的个数等于输出向量的维数。其将求和层的输出相除, 神经元j的输出为计算结果的第j个元素^{[10, 11]}。

$\begin{matrix} y_{j} = \frac{S_{Nj}}{S_{D}} j = 1, 2, \dots, k 。 \end{matrix}$ (6)

2 LS-SVM回归基本原理

支持向量机(SVM)在机器学习领域已经建立了比较完整的理论体系, 其理论基础是统计学习理论, 本质上是结构风险最小化的近似实现。对于一个给定的训练集合, 利用非线性映射把样本映射到高维特征空间。在特征空间中构造决策函数。这样原空间的非线性函数就转换成了特征空间中的线性函数^{[12, 13]}。

最小二乘支持向量机(LS-SVM)是标准支持向量机(SVM)的一种扩展形式, 与传统的支持向量机相比, 最小二乘支持向量机的损失函数采用误差的二范数, 并利用等式约束代替标准支持向量机的不等式约束, 从而将二次规划问题转化为线性方程组求解问题。降低了计算的复杂性, 从而提高了求解速度, 在很短的时间里已广泛用于许多领域^{[14, 15, 16]}。

对于有k个样本的训练集合(X_i, y_i), X_i∈ R^d, y∈ R, i=1, 2, …, k; 根据LS-SVM理论, 应用公式

$\begin{matrix} y (X) = ω^{T} φ (X) + b \end{matrix}$ (7)

在特征空间中对样本空间的非线性函数进行估计。其中:φ (X)是到高维空间的映射, ω 是权系数, b是偏差。当损失函数为误差的二范数时, ω 和b的确定转变成求解优化问题:

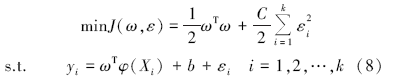
式中, ω 对应模型的泛化能力, C为惩罚因子, 控制模型的精度。

用拉格朗日法求解本优化问题

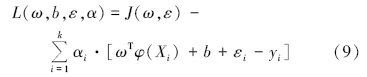
其中α 为Lagrange乘子, 根据优化条件可得

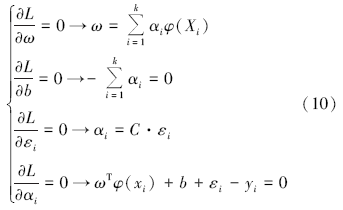
定义核函数K(X_i, X_j)=φ (X_i)· φ (X_j), 优化问题转化成求下面的线性方程组:

$\begin{matrix} [\begin{matrix} 0 & {I^{T}}_{d} \\ I_{d} & K + \frac{I_{d}}{C} \end{matrix}] [\begin{matrix} b \\ α \end{matrix}] = [\begin{matrix} 0 \\ y \end{matrix}] \end{matrix}$ (11)

式中:I_d是单位矩阵, I_d=(1, 1, …, 1)^T。则式(7)变为

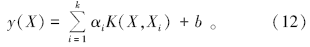
由此可知, 只要确定了核函数与惩罚因子, 就可以得到想要的向量机模型。

3 应用实例

在某煤田挑选了15口详查井的综合测井解释资料, 从中任意选出了有实验室分析的92层特征煤层, 其中73层的数据作为训练样本, 剩余的19层作为检验, 选择自然伽马、双收时差、密度以及三侧向电阻率这四个测井参数作为输入的特征参数, 水分、灰分、挥发分以及固定碳的含量这四个比较重要的工业分析指标为输出结果。利用MATLAB软件编程, 分别对上述两种方法的有效性进行了验证, 并对其结果进行了对比分析。

3.1 数据预处理

由于各个测井参数具有不同的物理意义, 其量纲和数量级有很大差别, 因此, 在进行计算前需对原始的数据进行归一化处理。处理公式为

$\begin{matrix} x_{g} = (x - x_{\min} \frac{)}{(} x_{\max} - x_{\min}), \end{matrix}$ (13)

式中:x_g为归一化后的数据, x为原始的测量数据, x_max、x_min分别为设定的最大值和最小值。经过处理后, 不同量纲的测井数据会在一个相同的数值范围内, 这样有利于提高计算的准确性。

3.2 GRNN网络与LS-SVM的实现

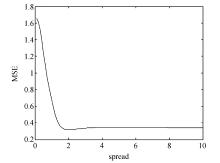
GRNN神经网络人为需要调节的参数比较少, 只有一个spread值需要调解。利用交叉验证的方法确定了网络最终的输入样本以及spread值。当spread值为2的时候, 网络的计算结果最为准确, 交叉验证的最小平均平方误差为0.32。

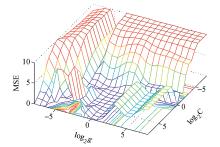
选用高斯径向基(RBF)函数作为LS-SVM的核函数, 在交叉验证中使用网格搜索方法确定了核参数与惩罚因子。当核参数(g)为0.19, 惩罚因子(c)为1.7时, 交叉验证的最小平均平方误差为0.47, 拟合效果最好。图2、图3示意了两种方法参数的选取, 表1给出了部分样本的训练误差。

	Figure Option View Download New Window
	图2 GRNN参数的选取

	Figure Option View Download New Window
	图3 LS-SVM 参数的选取

表1 73层训练样本的训练误差%

3.3 计算结果分析

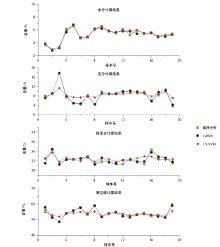
分别利用训练好的GRNN网络和LS-SVM对选取的19层数据进行计算, 结果见图4。可以看出:与LS-SVM相比, GRNN网络的计算结果更加准确, 水分、灰分、挥发分以及固定碳的平均平方误差均在1%以下(表2)。

	Figure Option View Download New Window
	图4 不同计算模型的输出结果

表2 GRNN与LS-SVM的平均平方误差%

由于GRNN网络计算的本质实际是观测样本的加权平均, 而其中权重为测试数据与样本之间的距离平方指数, 所以, 这四种组分的累加和会一直保持100%, 累加和的误差为0%, 符合常规的煤质解释模型。在LS-SVM计算模型中, 水分、灰分、挥发分以及固定碳这四种工业组分是分别进行拟合计算的, 所以计算的结果可能并不满足累加和为100%。但在对水分含量的计算上, LS-SVM的计算结果要优于GRNN神经网络。

4 结论

构建了基于GRNN神经网络和LS-SVM算法的计算模型, 实例分析表明, 这两种方法均能很好地应用在计算煤质工业组分方面。通过建立这种测井参数与工业组分之间的关系, 在不进行取样的情况下也能对煤层的组分进行分析。这两种方法中, GRNN网络的整体计算精度要高于LS-SVM。在算法进行学习的过程中, 有关参数的选取至关重要, 如何能快速、准确的确定出所选网络的计算参数是下一步的研究重点。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	曹炜. 煤田地质勘探中的煤质工作分析[J]. 科技与企业, 2014(10): 149. [本文引用:1]
[2]	周晓翠. 地球物理测井煤质分析[J]. 河北地质学院学报, 1986, 9(3-4): 401-412. [本文引用:1]
[3]	李大庆. 应用回归分析进行原煤灰分预测[J]. 物探与化探, 1989, 13(2): 116-122. [本文引用:1]
[4]	侯俊胜, 王颖. 神经网络方法在煤层气测井资料解释中的应用[J]. 地质与勘探, 1999, 35(3): 41-44. [本文引用:1]
[5]	孙致学, 姚军, 孙治雷, 等. 基于神经网络的聚类分析在储层流动单元划分中的应用[J]. 物探与化探, 2011, 35(3): 349-353. [本文引用:1]
[6]	吴东平, 岳晓燕, 吴春萍. 神经网络技术在煤层气测井评价中的应用[J]. 断块油气田, 2000, 7(5): 48-49. [本文引用:1]
[7]	戴黎明, 陈永良, 刘鑫, 等. 基于RBF神经网络的矿产资源潜力预测模型[J]. 物探与化探, 2011, 35(1): 103-108. [本文引用:1]
[8]	Specht D F. A general regression neural network[J]. IEEE Trans Neutral Networks, 1991, 2(6): 568-576. [本文引用:1]
[9]	金帅军. 基于GRNN 神经网络的农作物虫害量预测系统设计[D]. 呼和浩特: 内蒙古工业大学, 2013. [本文引用:1]
[10]	王小川, 史峰, 郁磊, 等. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. [本文引用:1]
[11]	钱光兴, 崔东文. RBF与GRNN神经网络模型在城市需水预测中的应用[J]. 水资源与水工程学报, 2012, 23(5): 148-152. [本文引用:1]
[12]	Vapnik V N. An Overview of Statistic Learning Theory[J]. IEEE Trans Neural, 1999, 10(5): 989-999. [本文引用:1]
[13]	Suykens J A K, Vand ewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, (9): 293-300. [本文引用:1]
[14]	阎威武, 朱宏栋, 邵惠鹤. 基于最小二乘支持向量机的软测量建模[J]. 系统仿真学报, 2003, 15(10): 1494-1496. [本文引用:1]
[15]	孙宗海, 孙优贤. 用于回归估计的最小二乘支持向量机[J]. 系统工程理论与实践, 2004, 24(7): 94-97. [本文引用:1]
[16]	牟丹, 王祝文, 黄玉龙, 等. 基于最小二乘支持向量机测井识别火成岩类型: 以辽河盆地中基性火山岩为例[J]. 吉林大学学报: 地球科学版, 2015, 45(2): 639-648. [本文引用:1]
[17]	张应文, 王亮, 王班友, 等. 煤田测井中煤层的定性及定厚解释技术应用[J]. 物探与化探, 2008, 32(1): 49-52. [本文引用:1]
[18]	董红, 侯俊胜, 李能根, 等. 煤层煤质和含气量的测井评价方法及其应用[J]. 物探与化探, 2001, 25(2): 138-143. [本文引用:1]

2014

0.0

... 在煤炭资源开发过程中,煤质的工业评价是很重要的一个方面^[1] ...

1986

0.0

... 近来,煤田测井无论是在仪器装备还是数据处理技术方面都得到了长足发展,多年的测井工作实践证明煤质的工业组分与测井参数之间有着一定的关系^[2,3] ...

1989

0.0

1999

0.0

... 神经网络等学习算法适合解决存在某种潜在联系但又无法确切表达的问题,在油气藏测井评价中已经得到广泛应用^[4,5,6,7] ...

2011

0.0

... 神经网络等学习算法适合解决存在某种潜在联系但又无法确切表达的问题,在油气藏测井评价中已经得到广泛应用^[4,5,6,7] ...

2000

0.0

... 神经网络等学习算法适合解决存在某种潜在联系但又无法确切表达的问题,在油气藏测井评价中已经得到广泛应用^[4,5,6,7] ...

2011

0.0

... 神经网络等学习算法适合解决存在某种潜在联系但又无法确切表达的问题,在油气藏测井评价中已经得到广泛应用^[4,5,6,7] ...

1991

0.0

... Specht 在1991年提出的一种径向基神经网络,具有很强的非线性映射能力、高度的鲁棒性以及柔性网络结构,适于解决非线性问题^[8] ...

2013

0.0

... 在结构上,GRNN由四层组成,如图1所示,分别为输入层、模式层、求和层和输出层^[9] ...

2013

0.0

... 其将求和层的输出相除,神经元j的输出为计算结果的第j个元素^[10,11] ...

2012

0.0

... 其将求和层的输出相除,神经元j的输出为计算结果的第j个元素^[10,11] ...

1999

0.0

... 这样原空间的非线性函数就转换成了特征空间中的线性函数^[12,13] ...

1999

0.0

... 这样原空间的非线性函数就转换成了特征空间中的线性函数^[12,13] ...

2003

0.0

阎威武, 朱宏栋, 邵惠鹤. 基于最小二乘支持向量机的软测量建模[J]. 系统仿真学报, 2003, 15(10): 1494-1496.

软测量技术在工业过程控制中得到了广泛的应用,对保证产品质量和安全生产有很重要的作用.软测量技术的核心问题是建立优良的软测量数学模型.支持向量机是近几年发展起来的机器学习的新方法,它较好地解决了小样本、非线性、高维数、局部极小点等实际问题.本文研究了基于最小二乘支持向量机的软测量建模方法,并用交叉验证的方法进行支持向量机参数选择.将基于最小二乘支持向量机的软测量模型应用于轻柴油凝固点的预估.结果表明最小二乘支持向量机是软测量建模的一种非常有效的方法.

... 降低了计算的复杂性,从而提高了求解速度,在很短的时间里已广泛用于许多领域^[14,15,16] ...

2004

0.0

孙宗海, 孙优贤. 用于回归估计的最小二乘支持向量机[J]. 系统工程理论与实践, 2004, 24(7): 94-97.

Least square generalized support vector machines (LS__GSVMs) are applied to regression estimation. LS__GSVMs' kernel functions have no or few limits when they are compared with standard support vector machines (SVMs). We give a presentation of quadratic programming (QP) problem for the LS__GSVMs. In order to solve the QP problem, we apply the combination of the gradient projection and successive overrelaxation (SOR) based on the matrix splitting. That is, we train the LS__GSVMs with above algorithm. Because...

提出了一种用于回归估计的最小二乘广义支持向量机.这种最小二乘广义支持向量机的核函数同标准的支持向量机相比没有或者只有很少的限制.将这种用于回归估计的最小二乘广义支持向量机表示成标准的二次规划(QP)问题,采用基于矩阵分裂的超松弛法同投影梯度法相结合的算法来解这一QP问题.根据超松弛法的特点,这一算法可以处理大量数据的情形.

... 降低了计算的复杂性,从而提高了求解速度,在很短的时间里已广泛用于许多领域^[14,15,16] ...

2015

0.0

牟丹, 王祝文, 黄玉龙, 等. 基于最小二乘支持向量机测井识别火成岩类型: 以辽河盆地中基性火山岩为例[J]. 吉林大学学报: 地球科学版, 2015, 45(2): 639-648.

Least squares support vector machine (LS-SVM) is a pattern recognition method developed from the statistical learning theory. Compared with the traditional statistics, LS-SVM can effectively resolve the problems of the finite of samples,non-linearity and high-dimension, and it can achieve accurate prediction. The essence of lithology identification is for classification. We take the advantage of the classification by LS-SVM: at first, the sample space is established by using the conventional logging curves of GR、CNL、DEN、AC、R LLD ; and then, the classifier of LS-SVM is optimized by searching optimal parameters using the simulated annealing algorithm and cross validation method; finally, the model of LS-SVM lithology identification is determined. Through the description of core section and the analysis of core/cuttings, 2 520 samples from the 315 m section of the 40 wells are taken as training samples in Liaohe basin, for establishing the standard of lithology identification. 110 928 logging data from 13 866 m section of the 8 wells are taken as the predicting samples. 8 types of volcanic rocks have been identified such as vesicular basalt,compact basalt,trachyte, et al. In comparison with the 316 samples from 8 wells,the corresponding identification rate is 75.2%. The accuracy and velocity of the LS-SVM lithology identification is improved distinctly compared with other well logging methods.

最小二乘支持向量机是在统计学习理论基础上发展起来的模式识别方法。与传统统计学相比,它能有效解决有限样本、非线性、高维数模型的建立问题,而且建立的模型具有很好的预测性能。岩性识别本质是解决分类问题,本文基于最小二乘支持向量机解决分类问题的优势,首先用 GR、CNL、DEN、AC、R LLD 等常规测井曲线数据建立样本空间;然后通过耦合模拟退火和交叉验证的方法寻找最佳参数,优化最小二乘支持向量机分类器;最后建立了最小二乘支持向量机岩性识别模型。通过取心段岩心描述和岩心/岩屑薄片鉴定,确定辽河盆地40口井315 m井段2 520个岩性样品作为训练样本,建立岩性识别标准。对8口井13 866 m井段110 928个火山岩数据采样点进行测井识别,可识别致密玄武岩、气孔玄武岩、粗面岩等8种主要火山岩类型。识别结果与8口测试井中316个有取心段岩心描述和岩心/岩屑薄片的精确岩矿定名对比,符合率达到75.2%,与以往测井识别复杂火山岩岩性相比,在识别准确率和效率上都有明显提高。

... 降低了计算的复杂性,从而提高了求解速度,在很短的时间里已广泛用于许多领域^[14,15,16] ...

2008

0.0

张应文, 王亮, 王班友, 等. 煤田测井中煤层的定性及定厚解释技术应用[J]. 物探与化探, 2008, 32(1): 49-52.

Three or more than three effective coalfield logging physical character parameters from the observational drill holes were used to analyze and compare anomalous characteristics of all curves for the purpose of detecting prominent features of coal seams and wall rocks and making qualitative interpretation of the bed of interest. The thickness-determining interpretation utilizes emphatically typical characteristic values of apparent resistivity and artificial radioactive curve anomalies to determine the depth, thickness and structure of the coal seam. The morphological feature, index horizon and correction method of the curve anomalies of various physical character parameters are sometimes also used to study individual coal seams.

选择使用观测钻孔内3种(含3种)以上有效的煤田测井物性参数,分析和对比所有曲线表现的异常特征,从中发现煤层与围岩的突出特性,达到对目的层的定性解释,而定厚解释是重点利用视电阻率和 γ-γ 曲线异常的典型特征值,确定煤层的深度、厚度和结构,有时还利用诸物性参数曲线异常的形态特征、标志层、对比方法,对个别煤层进行定位定论。

2001

0.0

董红, 侯俊胜, 李能根, 等. 煤层煤质和含气量的测井评价方法及其应用[J]. 物探与化探, 2001, 25(2): 138-143.

In the light of geological characteristics and statistical as well as logging data of the coalbed in the eastern depression of Liaohe Oilfield, the authors used regression to make industrial analysis of coalbeds and coal ranks. Through the analysis of coalbed gas characteristics and the utilization of Langmuir's equation, sorption isotherm and neutron background value of coalbed gas, the formulae for calculating coalbed methane content were deduced. The techniques were proved to be effective by the practical well log data from the eastern depression in Liaohe Oilfield.

根据辽河油田东部凹陷煤储层的地质特征以及实际煤岩芯分析资料和测井资料,利用回归分析方法得出了计算煤层各组分含量和煤阶的方法;通过分析煤层气特征,利用兰氏方程、吸附等温线和煤层气层中子背景值导出了煤层含气量的计算公式,并通过辽河油田东部凹陷实际煤储层测井资料的处理解释验证了方法的有效性。