根据双相介质地震波传播理论^[2], 可得到饱和流体孔隙介质运动方程^[11]

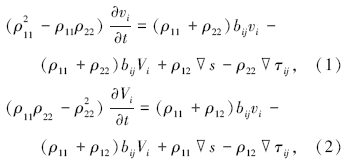
其中:i、j表示x、y、z三个不同方向分量, b_ij表示耗散系数, τ _ij为固相应力分量, s为作用在流体上的有效应力, v=(υ _x, υ _y, υ _z)^T为介质固体骨架速度矢量, V=(V_x, V_y, V_z)^T为介质流体速度矢量。令ϕ 为孔隙度, ρ ₁₁和ρ ₂₂分别表示单位体积内固体骨架和流体部分的有效质量, ρ ₁₂为流体相对固体骨架运动时的视质量^[12]。三者与固相密度ρ _s和流相密度ρ _f之间满足^[2]

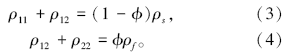
由饱和流体孔隙介质传播理论, 易得双相各向同性介质二维三分量一阶速度— 应力表达式。令Q_i表示固体骨架和流体空隙之间体积变化的耦合参数, R表示描述流体的弹性参数, 即将一定体积流体注入孔隙介质体积元, 保持总体积不变, 在流体上施加的一种力的度量^[12]。对于双相各向同性介质, 固相部分速度与应力之间的关系为

∂τxx∂x+∂τxz∂z∂τxz∂x+∂τzz∂z=∂∂t(ρ11υx+ρ12Vx)∂∂t(ρ11υz+ρ12Vz)+b1100b33∂∂t(υx-Vx)∂∂t(υz-Vz)。(5)

由广义达西定律可得Biot介质流相部分速度和应力关系式

∂s∂x∂s∂z=∂∂t(ρ12υx+ρ22Vx)∂∂t(ρ12υz+ρ22Vz)-b1100b33∂∂t(υx-Vx)∂∂t(υz-Vz)。(6)

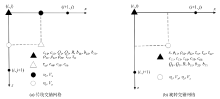
交错网格有限差分技术是一种有效的地震波正演模拟方法。传统交错网格是将网格剖分成整网格点和半网格点, 在相邻的两个时间层上的网格点处分别定义速度和应力分量, 并且在空间分布上相邻的两个时间层上的物理量恰好交错半个网格, 导数值在半网格点处计算, 以实现时间和空间的交错^[13]。由于速度和应力的相对关系, 对于不同的介质模型, 在计算过程中需要对部分场量和模型参数进行插值, 增加了计算误差, 降低了计算精度。网格定义、波场分量及弹性参数位置如图1a所示。

旋转交错网格由传统交错网格发展而来, 通过旋转对网格进行了重新划分和定义。与传统交错网格相比, 不同之处在于, 在同一网格点处仅定义同一物理量(速度、应力), 通过计算沿网格对角线物理量的差分来计算微分, 由于速度分量和应力分量分别定义在整网格点和半网格点上, 避免了部分场量和模型参数的插值^[14], 降低了计算误差, 提高了计算精度^{[15, 16]}。网格定义、波场分量及弹性参数位置如图1b^[17]。

图1

	Figure Option ViewDownloadNew Window
	图1 交错网格示意

稳定性问题是地球物理学研究中所必须解决的难题, 直接关系到数值模拟方法的成败。对于传统交错网格有限差分技术, 在相等步长的情况下, 时间域二阶、空间2M阶的稳定性条件满足

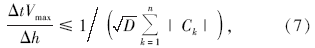
其中:Δ t是时间步长, D是空间维数, Δ h为空间步长, V_max为最大相速度, C_k是空间差分系数。

对于旋转交错网格有限差分技术, Saenger^[14]在Neumann稳定性条件下, 给出了在空间步长相等时, 时间域二阶、空间2M阶的稳定性条件为

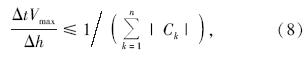
其参数意义同式(7)。

通过对比两种交错网格的稳定性条件可知, 相较于传统交错网格, 旋转交错网格有明显的优点, 在理论上有更宽松的稳定性条件。

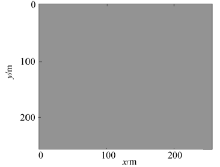
为观察旋转交错网格有限差分技术在双相各向同性介质中的模拟效果, 采用均匀各向同性介质为背景, 模型大小为256 m× 256 m, 网格间距1 m, 采样间隔0.1 ms, 震源采用Ricker子波, 位于模型中间位置, 加载于固相正应力处。模型如图2所示。取t=40 ms时的波场快照, 使用传统和旋转交错网格有限差分技术所得波场快照如图3、4所示。

图2

	Figure Option ViewDownloadNew Window
	图2 均匀双相各向同性介质模型

图3

	Figure Option ViewDownloadNew Window
	图3 均匀双相各向同性介质传统交错网格数值模拟波场快照

图4

	Figure Option ViewDownloadNew Window
	图4 均匀双相各向同性介质旋转交错网格波场快照

结合图3和图4可知, 使用传统和旋转交错网格有限差分技术对均匀双相各向同性介质模拟时, 均可以得到清晰的波场快照, 均匀双相介质中存在的快纵波、慢纵波和快横波都清晰可见, 波场特征十分明显, 波场分布符合地震波传播规律。说明了旋转交错网格有限差分技术可以较好地模拟地震波在均匀双相介质中的传播规律, 是一种有效的地震波场模拟方法。

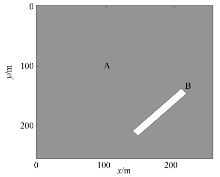
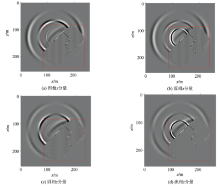
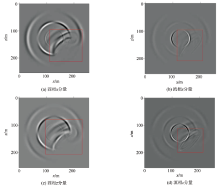
为进一步验证传统和旋转交错网格有限差分技术在双相各向同性介质模拟中的差异, 以非均匀双相各向同性介质为背景, 模型分为A、B两个区域, B是一密度和速度极小的地质异常区块, 其参数与均匀情况下相同。模型如图5所示。对非均匀双相各向同性介质分别使用传统交错网格技术和旋转交错网格技术进行波场模拟, 取t=40 ms时的波场快照进行对比, 所得波场快照如图6、7所示。

图5

	Figure Option ViewDownloadNew Window
	图5 非均匀双相各向同性介质模型

图6

	Figure Option ViewDownloadNew Window
	图6 非均匀双相各向同性介质传统交错网格数值模拟波场快照

图7

	Figure Option ViewDownloadNew Window
	图7 非均匀双相各向同性介质旋转交错网格波场快照

从图6可知, 当使用传统交错网格有限差分技术对双相介质进行波场模拟时, 除地质异常体外, 波场均可以正常传播, 符合双相介质波动理论, 而在地质异常体附近, 由于波场分量和模型参数的插值, 导致波场出现了振幅异常现象, 不能正确表示波场传播情况; 从图7可以观察到, 使用旋转交错网格有限差分技术模拟时, 波场传播均符合双相介质地震波传播规律, 在地质异常体附近有反射波和绕射波产生, 可以正确表示波场在双相介质中的传播。