引用本文
李午阳, 张健, 林巍. 基于CUDA的GPU并行优化重力三维反演[J]. 物探与化探, 2016,40(1): 179-184.
LI Wu-Yang, ZHANG Jian, LIN Wei. Regularized inversion of 3D gravity data:a new GPU parallelized method based on CUDA[J]. Geophysical and Geochemical Exploration, 2016,40(1): 179-184.
Doi:10.11720/wtyht.2016.1.32  
Permissions
Copyright©2016, 物探与化探编辑部
© 《物探与化探》编辑部
基于CUDA的GPU并行优化重力三维反演
李午阳1,2, 张健1,2, 林巍3
1.中国科学院大学 地球科学学院,北京 100049
2.中国科学院 计算与地球动力学实验室,北京 100049
3.犹他大学 地质与地球物理系,美国 盐湖城 84112

作者简介: 李午阳(1990-),男,现为中国科学院大学在读博士生,主要研究方向为非震地球物理正反演。

收稿日期: 2015-11-07
基金: 国家自然科学基金项目(41574074、41430319)
摘要

笔者介绍了一种在PGI Fortran平台上开发的重力三维GPU并行反演算法。该方法采用重加权正则化共轭梯度算法(Re-Weight Regularized Conjugate Gradient),可以在具有NVIDIA显卡的个人计算机上使用CUDA进行并行计算,无需借助工作站即可实现几十至上百倍的计算加速,提供稳定可信的反演结果。并对可视化操作系统进行了优化,实现了在高端计算机系统上亿网格点的反演计算,同时在中、低端计算机也可以实现加速。模型计算结果表明,该算法是一种高效且可靠的重力三维反演并行方法。

关键词: 重力; 三维反演; CUDA; GPU; 并行计算; 共轭梯度法
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2016)01-0179-06 doi: 10.11720/wtyht.2016.1.32
Regularized inversion of 3D gravity data:a new GPU parallelized method based on CUDA
LI Wu-Yang1,2, ZHANG Jian1,2, LIN Wei3
1.College of Earth Science,University of Chinese Academy of Sciences,Beijing 100049
2.Key Laboratory of Computational Geodynamics,Chinese Academy of Sciences,Beijing 100049
3.Department of Geology and Geophysics,University of Utah,Salt Lake City 84112
Abstract

We introduce a new 3D parallelgravity inversion method based on CUDA GPU in PGI Fortran,which could be used in PCs and Laptops with NVDIA graphic cards to accelerate iteration speed for Re-Weight Regularized Conjugate Gradient method up to hundreds times.Storage and threads optimization was made for visual OS, leading a more than 0.1 billion cell's number for inversion in PCs.The result of model study shows that this method is an efficient and believable parallel computing algorithm.

Keyword: gravity; 3D inversion; GPU; CUDA; parallel computing; RCG method

重力勘探由于其成本较低、施工方法方便等, 被广泛应用于大尺度的地质异常体勘查、大范围找矿普查、以及小比例尺密度三维地质建模等工作中。目前常用的反演方法有两种, 2.5维联合3维界面反演[1, 2]和三维物性反演。通过对地下介质进行三维网格剖分, 反演每个网格单元的物性, 从而得到地质异常体的物性分布与形态特征[3]。

对于复杂结构目标体的三维反演, 由于受到数据计算与存储量的限制, 主要采用的是三维物性反演。即便如此, 重力场计算的三维正演模拟和反演中依旧面临着很大的数据处理量, 使用传统的线性反演, 往往数百万个网格点的计算就会超过个人计算机的内存处理范围。由于计算机内存与CPU计算效率的瓶颈, 很大程度上限制了数据处理解释工作的品质。为了解决这个问题, 近十几年来, 并行计算成为了主流的研究方向。Chen等[4, 5]采用了基于C语言的CUDA代码实现了重力的三维正演成像; 林巍等[6]利用GPU遗传算法实现了海洋重力三维反演; Cuma等[7, 8]实现了基于CPU的OpenMP算法加速与基于GPU的OpenACC算法加速, 提供了在服务器等高性能计算机集群上实现重力反演计算的方法。从硬件结构上来看, 相较于目前仅有数个、数十个核的CPU, 拥有数百甚至数千个核的GPU在处理大数据量的简单运算, 如重力反演大矩阵运算上, 有着天然的优势。

笔者在PGI Fortran平台上采用传统Fortran语言与CUDA语言混编, 将重加权正则化共轭梯度(Re-weighting Regularized Conjugate Gradient, RRCG)三维重力场反演算法进行重组, 使其可以在个人台式计算机与笔记本计算机上使用GPU进行并行计算, 正则化的使用使反演结果稳定可信、具有物理意义; 放弃存储敏感度矩阵A, 从而使得计算效率与数据处理量同时得到提高; 引入了线程多次调用与敏感度范围(footprint)搜索, 实现了存储扩容与反演加速。为了验证程序的正确性, 我们采用相同算法的MATLAB传统代码进行了比对测试。该方法可以有效的在个人计算机上解决上亿网格点的反演计算问题, 为解决大数据量的三维重力反演提供了新的方法思路。

1 正演与反演
1.1 正演算法

虽然对于重力分量体积分的解析解是可以直接求取的, 但为考虑并行计算的效率, 笔者仍采用常用的离散化单点积分:将地下介质划分成均匀的立方体网格, 并假设网格内部密度均匀统一, 经过网格离散化以后, 在重力测量中常用的垂直分量计算公式可以表示为

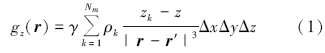
离散形式。其中:γ 表示万有引力常数; Nm表示立方体网格总数; k表示网格点编号; 矢量r'= (x', y', z'), r=(x, y, z)分别表示观测点和源网格中心点的位置; z和z'分别表示观测点和源中心点在垂直方向上的位置; Δ x, Δ y, Δ z分别表示划分立方体网格沿相对坐标轴三个方向的长度; ρ 表示立方体网格的密度。

在这种条件下, 求观测点重力异常值的过程可以看成是一个线性算子A与密度分布矢量m之间的运算

d=Am, (2)

其中:d表示为一个长度为Ndata的观测点空间分布矢量, m表示为一个长度为Mcell的空间密度分布矢量, A表示重力垂直分量的线性算子, 在这样的线性问题下, A也是反演问题中的敏感度矩阵。

1.2 反演算法

考虑到并行计算速度, 笔者在反演中采用的是重加权的正则化共轭梯度(RRCG)算法, Tikhonov正则化的引入, 可以压制由于数据噪声与多解性引起的反演结果不稳定与物理意义不明确 [9, 10], 而不同的加权因子可以在平滑解与有明显边界的解之间进行平衡, 重加权(Re-weighting)可以在迭代过程中动态调整正则化因子α 的范围, 可以在保证数据品质的前提下加快收敛速度。笔者仅介绍与并行计算相关的算法流程, 对于加权因子与正则化因子的选择与更新方式不再介绍, 可详见文献[9]。

RRCG反演算法求取的是参数泛函(Parameter Functional)的极小值, 其完整形式可以表示为

Pα(m)=(WdAm-Wdd)T(WdAm-Wdd)+α(WeWmm-WeWmmapr)T(WeWmm-WeWmmapr), (3)

其中:d为观测数据矢量; m为模型矢量; A为正演算子; mapr是先验模型矢量; α 是正则化参数, 用来平衡右式第一项误差泛函(misfit functional)与第二项稳定泛函(stabilizer functional); Wd、Wm分别是数据和模型加权矩阵, We是聚焦加权矩阵。在位场反演中, 不对观测数据加权, 即Wd为单位矩阵, 而Wm与We皆为对角阵, 针对不同问题有不同的调整方法。

共轭梯度法的是计算是用迭代计算替代求逆矩阵计算, 迭代计算的每一步的计算流程如下[11]

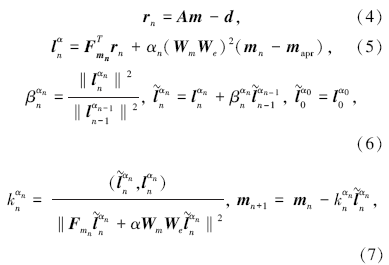
其中:rn表示剩余误差矢量; n表示迭代次数; ln表示梯度法迭代方向矢量, l˙n表示共轭梯度法迭代方向矢量; F表示Frechet导数矩阵; 在线性反演问题中F=A; kn表示每一次迭代的迭代步长; α n是每一步迭代的正则化参数。

传统的串行RRCG反演中需要计算、存储敏感度矩阵A并反复读取, 顺序计算每一个迭代步骤, 直到迭代满足次数条件或误差条件从而停止。A矩阵是一个与数据及模型尺度相乘有关的大矩阵, 在大型三维反演中存储和读取耗时且困难, 成为限制常规RRCG线性反演的重要因素。

2 GPU算法设计
2.1 GPU与CUDA

GPU(Graphics Processing Unit), 即图形处理单元, 计算方式高度并行, 计算能力强大, 被早期的科研工作者用于提高通用计算的计算速度。而近十年来, 由于CUDA的出现, 才使得GPU成为一种不需要掌握图形计算基础就可以使用的通用并行计算工具[12]。CUDA(Compute Unified Device Architecture)是由NVIDIA提供的通用GPU编程语言架构, 目前可以支持在C、Fortran、Matlab等多种语言平台下使用CUDA语句调用GPU计算单元进行并行计算。

CUDA是最适合应用在位场线性三维反演中的并行计算手段之一。首先, 采用RRCG反演方法, 其流程是用迭代算法, 每个计算步骤都可以简化为相互独立的矩阵与矢量进行简单运算, 为并行计算提供了条件; 其次, 与传统的CPU串行或并行相比, GPU的计算核心数量有绝对领先的优势, 相较于目前高端个人计算机拥有的16个或32个计算核心, 个人显卡即可拥有400~600个, 甚至最高超过2000个GPU计算核心; 最后, 相比于最近发布的另一种GPU计算标准OpenACC, 虽然CUDA需要更多的对计算过程的控制和分配, 即更多的对于常规反演代码的改编, 但同时留有更多对显存地控制和深度开发的余地。

与此同时, 在拥有良好的算法结构与计算控制的情况下, 与OpenACC相比, CUDA的计算效率可以最多提高一倍以上[13]。因此, 笔者采用了基于PGI Fortran的CUDA作为并行算法的开发平台。

2.2 RRCG反演的并行设计

RRCG反演迭代流程中的每一步计算结果皆为标量或矢量而非矩阵, 在实际运算中, 标量与矢量相互间的运算速度非常快, 可交由CPU计算, 而需要并行的部分是与敏感度矩阵A及其转置有关的矩阵运算。可以按照计算方式将并行部分分为两类:数据尺度Ndata的并行, 即与A矩阵有关的矩阵运算, 计算结果为数据长度的矢量Ipar; 模型尺度Mcell的并行, 与A矩阵转置有关的矩阵运算, 计算结果为模型尺度Mcell的矢量Jpar。由此, 可以将迭代公式改写为

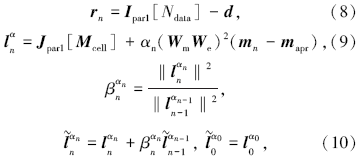
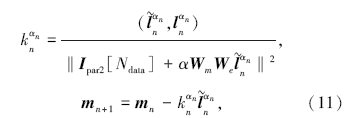
其中:矢量Ipar1、Ipar2与Jpar1分别代表了上文所述的两类并行化的矩阵运算的结果。

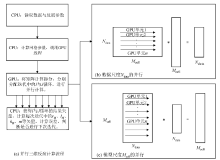
将矩阵与矢量的乘积运算拆分, 分配给GPU计算单元, 让每个单元独立进行网格体积、观测点距离等计算, 只输出结果矢量。通过这样的调整, 无需像传统方法一样预先将庞大的敏感度矩阵A存入系统内存, 大大降低了对系统内存的需求(图1b、1c); 且每次重新计算与A矩阵有关的矢量所消耗的时间要远远低于访问庞大矩阵所花费的时间, 提高了计算效率。对于无需并行的部分, 交由CPU进行串行计算, 迭代计算流程如图1a所示。

图1 并行化RRCG三维反演计算流程

2.3 计算效率

为验证并行计算的加速效率, 将并行代码与采用相同反演算法的常规串行代码进行计算时间比较, 比较代码的计算结果由犹他大学蔡红柱博士提供, 编程平台为MATLAB, 重力垂直分量模拟测量点5 000个。计算数据在同一台中端笔记本计算机上获得, 该机型拥有16Gb内存, CPU是拥有4核8线程的i7-4710, 主频率为2.50 GHz; 显卡为GeForce860 m, 拥有640个GPU计算单元与4 Gb显存, 使用其中的512个单元, 下文中所涉及的所有计算均采用相同配置。计算时间如表1所示。

表1 串行与并行代码RRCG反演单次迭代计算时间对比

从表中可以看出, 随着网格数量的增加, 传统串行方法中对敏感度矩阵A的计算与存储将会占用大量的计算时间与内存, 当网格数量达到100万以上时, 16 Gb的计算机内存已经不足以支持存储A矩阵。相反, 经过GPU并行的反演算法, 由于矩阵运算已经分配到GPU计算单元中, 只存储与A及其转置矩阵有关的矢量, 即矢量I与J, 从而克服了内存占用的瓶颈, 迭代计算时间也仅仅表现出随网格数量增加而近似线性增加的关系。

综上, 通过将重力三维反演直接并行化, 已经可以实现在相同整机配置水平下CPU计算性能的几十甚至几百倍的加速。然而由于GPU使用本身的原因, 单次迭代时间被限制在了5 s以内, 从而网格点数量被限制在了400万左右。将介绍两种优化计算的方法, 进一步提高计算网格上限与计算速度。

3 优化计算技术
3.1 线程多次调用

个人计算机常用的操作系统, 无论是Linux、Mac或windows, 都拥有可视化桌面(Visual Windows)功能, 当使用CUDA语言调用GPU线程进行工作时, 单次运算的时间如果超过5~15 s, 为保护可视化界面的正常功能, 并行计算将会被系统强制停止, 这种问题称之为“ 调用瓶颈” 。为此, 采取GPU线程多次调用技术, 尽可能的将GPU计算单元的单次时间使用压制在5 s以内。

具体做法是在CPU调用GPU线程之前, 将单个GPU核心的计算量以Mcell的整数倍进行切割, 减少GPU计算单元内部的loop循环大小, 从而减少单次计算时间。在计算Ipar矢量时, 由于每次调用仅计算每一个数据点的部分结果, 对计算结果进行累加即得到完整的迭代解。而计算Jpar矢量时, 则需要对每次调用的运算结果进行矢量拼接。

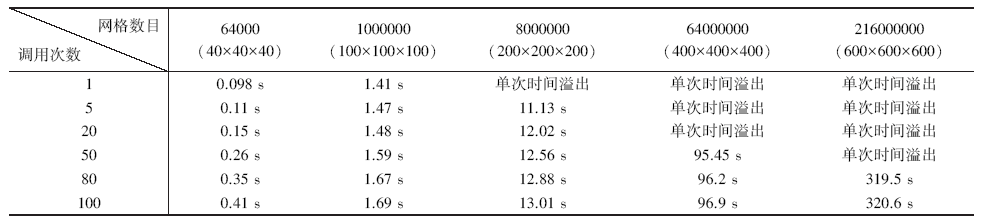
对多次调用优化后的代码进行了单次迭代时间测试, 结果如表2所示, 其中单次时间溢出表示单次线程计算时间超过调用瓶颈。结果表明, 多次调用线程可以克服GPU计算吞吐量与调用的瓶颈, 大大的增加计算网格的数量, 如不考虑时间成本, 可以提高到百亿级别; 计算时间与计算网格数量的大小呈明显线性关系, 而由于多次调用增加的CPU与GPU通讯时间的开销可以忽略不计; 同时可以预见的是, 该方法使得计算速度较差的低端图形处理器同样可以克服调用瓶颈, 达到扩大计算网格量的目的。

表2 不同网格数目与线程调用次数情况下的单次迭代时间对比
3.2 敏感范围搜索

采用的另一种优化技术是敏感度范围搜索, 这是一项目前在航空电磁、重力、重力梯度等反演中较为广泛使用的计算优化技术[7, 14, 15]。不同的地球物理场之间有着不同的影响范围, 对于单个观测点而言, 在某个范围外的异常体对其造成的影响几乎可以忽略, 这个范围就被称作为敏感范围, 即footprint。如重力垂直分量的反演中, 可以仅考虑约20 km范围以内的密度异常体对观测点的影响, 这对于上百公里尺度的航空重力反演而言, 可以很大幅度的减少计算量。笔者对于敏感范围搜索的主要创新在于, 在多次线程调用代码结构下实现了敏感范围搜索算法。

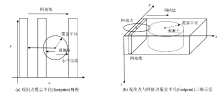
如图2所示, 在线程多次调用结构下, 每个GPU计算节点单次处理的网格数量由整个计算域变成了顺序排列的“ 网格墙” 。我们采用了一种圆柱形的敏感范围计算方法, 即只判定水平距离。当计算Ipar矢量时, 如果观测点的敏感度覆盖半径小于观测点到网格墙水平距离的最小值时, 则抛弃整堵“ 墙” , 进入下一次GPU调用。反之, 则计算每个网格点与观测点的水平距离, 判断其是否在计算覆盖半径以内(图2a)。当计算Jpar矢量时, 则计算其对覆盖半径内的所有观测点的影响(图2b)。

图2 线程多次调用结构下的GPU并行敏感范围搜索示意

综上, 多次调用线程的使用, 提高了并行算法的最大适用网格数。在此基础上引入的敏感范围搜索, 又进一步在面对大尺度的重力反演中, 成比例的减少迭代计算时间。

4 模型计算

为验证并行程序的正确性与有效性, 设计一个长、宽均为50 km, 深度30 km的反演区域, 区域中心安放了密度异常为Δ ρ =1 g/cm3, 长、宽、高分别为10km、 10 km与1 km的密度异常体薄板, x方向中轴截面如图3b中所示, 正演网格采用了x· y· z三方向100× 100× 60设计, 边长为500 m, 得到正演拟合等值面如图3a中所示。

图3 模型计算参数与结果

分别采用了50× 50× 30 与100× 100× 30的网格数量进行反演计算, 并50× 50× 30传统串行反演进行比对。为验证优化算法正确性, 并行代码中强行设置了分五次调用GPU线程, 并设置了20 km的敏感度范围, 而串行代码中使用常规RRCG方法。反演设定误差小于5%时停止迭代, 结果如图3中所示。同等网格条件下的并行计算反演结果与传统RRCG方法所得结果基本一致, 验证了上述优化算法代码的正确性。而在传统RRCG算法已经内存溢出的细网格条件下, 并行计算结果更真实的反映了异常体的形态与峰值, 体现了在大尺度重力计算中, 优化后的并行计算在反演精度上的优势。

5 结论与建议

1) 通过CUDA语言GPU的并行算法设计, 提高了RRCG反演计算的效率与计算容量; 采用优化算法进一步提高了海量三维网格处理的能力与计算速度。算法通过了模型计算比较, 结果正确可信。该方法为解决重力大型三维反演提供了一种思路。

2) 未来工作中可以将该方法推广到实际的大尺度海洋、航空重力反演中; 算法方面, 可以进一步开发磁法与重磁张量反演, 以及重磁联合反演和三维地质建模。

The authors have declared that no competing interests exist.

参考文献
[1] Lü Q, Qi G, Yan J. 3D geologic model of Shizishan ore field constrained by gravity and magnetic interactive modeling: A case history[J]. Geophysics, 2012, 78(1): B25-B35. [本文引用:1]
[2] Wang G, Zhang S, Yan C, et al. Mineral potential targeting and resource assessment based on 3D geological modeling in Luanchuan region, China[J]. Computers & Geosciences, 2011, 37(12): 1976-1988. [本文引用:1]
[3] 姚长利, 郝天珧. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2): 252-258. [本文引用:1]
[4] 陈召曦, 孟小红, 刘国峰, 等. 基于 GPU 的任意三维复杂形体重磁异常快速计算[J]. 物探与化探, 2012, 36(1): 117-121. [本文引用:1]
[5] Chen Z, Meng X, Guo L, et al. GICUDA: A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA[J]. Computers & Geosciences, 2012, 46: 119-128. [本文引用:1]
[6] 林巍, 张健, 李家彪. 南沙中业群礁地区中生代残留盆地 GPU 重力异常三维反演[J]. 热带海洋学报, 2013, 32(4): 36-42. [本文引用:1]
[7] Cuma M, Wilson G A, Zhdanov M S. Large-scale 3D inversion of potential field data[J]. Geophysical Prospecting, 2012, 60(6): 1186-1199. [本文引用:2]
[8] Cuma M, Zhdanov M S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs[J]. Computers & Geosciences, 2014, 62: 80-87. [本文引用:1]
[9] Zhdanov M S. New advances in regularized inversion of gravity and electromagnetic data[J]. Geophysical Prospecting, 2009, 57(4): 463-478. [本文引用:2]
[10] Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. [本文引用:1]
[11] Zhdanov M S. Geophysical inverse theory and regularization problems[M]. Elsevier, 2002. [本文引用:1]
[12] Cook S. CUDA programming: a developer's guide to parallel computing with GPUs[M]. Newnes, 2012. [本文引用:1]
[13] Hoshino T, Maruyama N, Matsuoka S, et al. CUDA vs openACC: Performance case studies with kernel benchmarks and a memory-bound CFD application[C]//Cluster, Cloud and Grid Computing (CCGrid), 2013 13th IEEE/ACM International Symposium on. IEEE, 2013: 136-143. [本文引用:1]
[14] Zhdanov M S, Smith R B, Gribenko A, et al. Three-dimensional inversion of large-scale EarthScopemagnetotelluric data based on the integral equation method: Geoelectrical imaging of the Yellowstone conductive mantle plume[J]. Geophysical Research Letters, 2011, 38(8): 1-7. [本文引用:1]
[15] Cox L H, Wilson G A, Zhdanov M S. 3D inversion of airborne electromagnetic data using a moving footprint[J]. Exploration Geophysics, 2010, 41(4): 250-259. [本文引用:1]