位场高阶导数的波数域迭代法

引用本文

王彦国, 张瑾. 位场高阶导数的波数域迭代法[J]. 物探与化探, 2016,40(1): 143-147.
WANG Yan-Guo, ZHANG Jin. The iterative method for higher-order derivative calculation of potential fields in wave number domain[J]. Geophysical and Geochemical Exploration, 2016,40(1): 143-147.
Doi:10.11720/wtyht.2016.1.25 复制到剪切板

Permissions

位场高阶导数的波数域迭代法

王彦国, 张瑾

东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌 330013

作者简介: 王彦国(1985-),男,讲师,主要从事位场数据处理方法技术研究。E-mail:wangyg8503@126.com

收稿日期: 2015-04-15

基金: 国防项目(科工局[2013]969号)及东华理工大学科研基金(DHBK2013213)联合资助

摘要

位场导数换算是位场数据处理和解释的基本方法,但其不稳性限制了高阶导数在实际资料处理中的应用。针对于此,提出了位场高阶导数的波数域迭代法。在导数算子中引入一个包含求导阶次和高阶导数算子本身相关的低通滤波器,然后通过迭代法进行逐次逼近,进而得到高阶导数波数域迭代法的递推公式;同时证明了该方法的收敛性,对比分析了迭代法与常规方法导数算子的滤波特性。在高阶导数的模型检验和实例应用中,迭代法与常规方法的对比分析结果表明,迭代法具有稳定性强和计算精度高的优点。

关键词: 高阶导数; 迭代法; 收敛性; 滤波特性; 稳定性

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)01-0143-05 doi: 10.11720/wtyht.2016.1.25

The iterative method for higher-order derivative calculation of potential fields in wave number domain

WANG Yan-Guo, ZHANG Jin

Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China Institute of Technology,Nanchang 330013,China

Abstract

Derivative calculation is a basic method used in data processing and interpretation of potential fields,but the instability of the result restricts the application of higher-order derivative in practical data.Thus,this paper proposes an iterative method for higher derivative calculation of potential fields to resolve the problem of instability.The authors added a lowpass filter which contained the derivative order number and derivative operator to the higher derivative operator,and used the iterative method to perform successive approximation.On such a basis,the authors deduced the recursive formula of the iterative method of higher-order derivative.In addition,the authors proved the convergence of the iterative method and made a comparative analysis on filtering characteristics of derivative operator by using different methods. In model test and application,the comparative analysis of the results of the iterative method and conventional method for higher-order derivative indicates that the iterative method has advantages of stronger stability and higher calculation accuracy.

Keyword: higher-order derivative; iterative method; convergence; filtering characteristic; stability

Show Figures

在位场数据处理中, 高阶导数具有重要的物理意义。它在不同形状地质体上有不同的特征, 有助于异常的划分和解释; 在一定程度上可以划分不同深度和大小异常源产生的叠加异常, 且导数的阶次越高, 这种分辨能力就越强^{[1, 2]}。同时导数换算也是位场数据处理和反演方法技术的核心运算, 如:重力归一化总梯度法^{[3, 4]}、欧拉反褶积法^{[5, 6]}、解析信号法^{[7, 8, 9]}, 位场数据导数换算结果的好坏直接关系到这些反演方法的应用效果。

目前, 位场数据的导数换算大多在空间域或波数域中进行。空间域主要有最小二乘法、拉格朗日插值法^[10]、样条函数插值法^[11]等方法, 但这类方法存在着计算精度低和计算速度慢的缺点。波数域主要采用Fourier变换^{[12, 13]}, 然而波数域中的导数响应因子本身具有高频放大作用, 尤其求导阶次越高, 数据因截断产生的吉布斯效应以及随机干扰的放大作用越强。为了压制高阶导数的不稳定性, 一般采取附加低通滤波器来达到压制高频干扰的目的^[14], 如向上延拓、维纳滤波、正则化滤波等。目前人们普遍认为:采用向上延拓一定高度的方法来压制导数换算中的高频成分最为方便和实用^[15]。而事实上, 向上延拓算子不仅压制了高频成分, 同时也对低频成分进行了消弱, 由此计算的导数值与实际的导数值存在着偏差。基于此, 在前人对迭代法的研究基础上^{[16, 17, 18]}, 结合高阶导数算子的滤波特性, 提出了位场高阶导数的波数域迭代法, 并对该方法进行了模型检验及实际应用。

1 波数域迭代法的基本原理及其收敛性证

明和滤波特性分析1.1 高阶导数迭代法的基本原理

在波数域中, 位场数据的x、y、z三方向任意阶导数波谱可以表示为

$\begin{matrix} S_{(m, p, q)} (u, v) = φ_{x}^{(m)} \cdot φ_{y}^{(p)} \cdot φ_{z}^{(q)} \cdot S (u, v), \end{matrix}$ (1)

其中:S₍_m_,_p_,_q₎(u, v)和S(u, v)分别为所求导数波谱和原始异常波谱; $\begin{matrix} φ_{x}^{(m)} \end{matrix}$ =(iu)^m、 $\begin{matrix} φ_{y}^{(p)} \end{matrix}$ =(iv)^p、 $\begin{matrix} φ_{z}^{(q)} \end{matrix}$ =( $\begin{matrix} \sqrt[]{u^{2} + v^{2}} \end{matrix}$ )^q分别为x方向m阶导数算子、y方向p阶导数算子和z方向q阶导数算子; u、v分别是x、y方向的波数。

由式(1)可知, 求导阶次l和理论导数算子φ ₍_m_,_p_,_q₎分别为

$\begin{matrix} l = m + p + q, φ_{(m, p, q)} = φ_{x}^{(m)} \cdot φ_{y}^{(p)} \cdot φ_{z}^{(q)} 。 \end{matrix}$ (2)

将φ ₍_m_,_p_,_q₎代入式(1)中, 则有

$\begin{matrix} S_{(m, p, q)} = φ_{(m, p, q)} \cdot S 。 \end{matrix}$ (3)

一般来说, 求导阶次l越大, 导数算子φ ₍_m_,_p_,_q₎引起的高频振荡越明显, 则需对高频成分压制越强; 且φ ₍_m_,_p_,_q₎对不同方向的频率放大作用不同, 为此在这里对S₍_m_,_p_,_q₎乘以一个包含求导阶次l和导数算子φ ₍_m_,_p_,_q₎相关的低通滤波器P, 即

$\begin{matrix} P (l, φ_{(m, p, q)}) = \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}, \end{matrix}$ (4)

其中:参数α ≥ 1, β > 0, (文中选取α =1, β =1), |φ ₍_m_,_p_,_q₎|是φ ₍_m_,_p_,_q₎的绝对值数值形式。那么经P滤波后的S₍_m_,_p_,_q₎近似值(在此称为一阶近似谱)可表示为

$\begin{matrix} S_{(m, p, q)}^{(1)} (u, v) = \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot S (u, v), \end{matrix}$ (5)

将 $\begin{matrix} S_{(m, p, q)}^{(1)} \end{matrix}$ 代入式(3)中, 得S的一阶近似值

$\begin{matrix} S^{(1)} (u, v) = \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot S (u, v), \end{matrix}$ (6)

再用S和S⁽¹⁾的差值对 $\begin{matrix} S_{(m, p, q)}^{(1)} \end{matrix}$ 进行校正, 得S₍_m_,_p_,_q₎的二阶近似值

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(2)} (u, v) = S_{(m, p, q)}^{(1)} (u, v) + \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot [S (u, v) - S^{(1)} (u, v)] 。 \end{matrix} \end{matrix}$ (7)

重复以上步骤, 得S₍_m_,_p_,_q₎的n阶近似值

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(n)} (u, v) = S_{(m, p, q)}^{(n - 1)} (u, v) + \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot [S (u, v) - S^{(n - 1)} (u, v)] 。 \end{matrix} \end{matrix}$ (8)

由式(3)可知

$\begin{matrix} \begin{matrix} \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot S^{(n - 1)} (u, v) = \\ \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot S_{(m, p, q)}^{(n - 1)} (u, v), \end{matrix} \end{matrix}$ (9)

代入式(8), 得

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(n)} (u, v) = [1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}] \cdot \\ S_{(m, p, q)}^{(n - 1)} (u, v) + \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} \cdot S (u, v) 。 \end{matrix} \end{matrix}$ (10)

令 $\begin{matrix} g_{(m, p, q)}^{(n)} \end{matrix}$ 、 $\begin{matrix} g_{(m, p, q)}^{(n - 1)} \end{matrix}$ 分别是第n、n-1次迭代得到的波谱 $\begin{matrix} S_{(m, p, q)}^{(n)} \end{matrix}$ 、 $\begin{matrix} S_{(m, p, q)}^{(n - 1)} \end{matrix}$ 的傅里叶反变换, ε 为给定的较小正实数。当迭代过程中满足max| $\begin{matrix} g_{(m, p, q)}^{(n)} \end{matrix}$ - $\begin{matrix} g_{(m, p, q)}^{(n - 1)} \end{matrix}$ |≤ ε 时终止迭代, 此时可认为所求导数g₍_m_,_p_,_q₎≈ $\begin{matrix} g_{(m, p, q)}^{(n)} \end{matrix}$ 。

1.2 收敛性证明

迭代法的正确与否直接取决于该方法是否收敛于理论解, 在此采用递推法及数学归纳法对递推公式(10)进行收敛性证明。

当n=1时, 见式(5);

当n=2时, 由式(5)和式(10)得

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(2)} (u, v) = [1 + 1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}] \cdot \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} S (u, v) 。 \end{matrix} \end{matrix}$ (11)

当n=3时, 由式(10)和式(11)得

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(3)} (u, v) = \{1 + 1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} + \\ {[1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}]}^{2}\} \cdot \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} S (u, v) 。 \end{matrix} \end{matrix}$ (12)

由公式(5)、(10)、(11)和(12), 利用数学归纳法很容易得到迭代通式(证明略)

$\begin{matrix} \begin{matrix} S_{(m, p, q)}^{(n)} (u, v) = \{1 + 1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} + \dots + \\ {[1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}]}^{n - 1}\} \cdot \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} S (u, v) 。 \end{matrix} \end{matrix}$ (13)

显然, 式(13)右边中括号内的式子为一等比数列, 其公比0≤ 1- $\begin{matrix} \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} \end{matrix}$ < 1, 因此 $\begin{matrix} S_{(m, p, q)}^{(n)} \end{matrix}$ 极限存在

$\begin{matrix} \begin{matrix} S_{(m, p, q)} (u, v) = \lim_{n \to \infty} S_{(m, p, q)}^{(n)} (u, v) = \\ \frac{1}{1 - [1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}]} \cdot \\ \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} S (u, v) = φ_{(m, p, q)} S (u, v) 。 \end{matrix} \end{matrix}$ (14)

上述收敛性证明过程表明, 在理论上利用本文提出的迭代法进行高阶导数换算是可以收敛到理论解的; 且由于迭代过程中的每一步事实上都是一次稳定的低通滤波处理, 这在理论上保证了迭代法的稳定性。

1.3 滤波特性分析

滤波器具有频率选择、滤除噪声和分离场的作用, 研究滤波器的滤波特性在频率域数据处理中具有重要的意义。为此, 我们在这里对理论导数算子φ ₍_m_,_p_,_q₎、本文迭代法的导数算子 $\begin{matrix} φ_{(m, p, q)}^{(n)} \end{matrix}$ 的滤波特性进行了对比分析。其中

$\begin{matrix} \begin{matrix} φ_{(m, p, q)}^{(n)} = \{1 + 1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}} + \dots + \\ {[1 - \frac{1}{(α + β | φ_{(m, p, q)} {|)}^{l}}]}^{n - 1}\} \frac{φ_{(m, p, q)}}{(α + β | φ_{(m, p, q)} {|)}^{l}} 。 \end{matrix} \end{matrix}$ (15)

图1给出了垂向一阶导数算子(m=p=0, q=1)和垂向二阶导数算子(m=p=0, q=2)迭代滤波响应特征曲线。图中可以看出:①理论导数算子φ ₍_m_,_p_,_q₎随着频率的增加急剧上升, 且导数阶次越高, 高频成分被放大的越强; ②迭代导数算子 $\begin{matrix} φ_{(m, p, q)}^{(n)} \end{matrix}$ 在低频段逼近φ ₍_m_,_p_,_q₎, 保证了低频有用信号得以较好的导数转换, 在高频段小于φ ₍_m_,_p_,_q₎, 从而使高频干扰的放大作用得以压制; ③随着迭代次数的增加, 迭代导数算子 $\begin{matrix} φ_{(m, p, q)}^{(n)} \end{matrix}$ 逐渐趋于φ ₍_m_,_p_,_q₎; ④当迭代次数不变时, 随着导数阶次的增加, $\begin{matrix} φ_{(m, p, q)}^{(n)} \end{matrix}$ 对高频成分的压制作用更为明显, 这保证了高阶导数计算的稳定性。

	Figure Option View Download New Window
	图1 迭代法滤波特性a— 垂向一阶导数; b— 垂向二阶导数

可知, 本文迭代法的导数响应算子在低频段能精确地逼近理论导数算子, 对高频成分则能有效压制, 因而方法在理论上具有保幅性和稳定性的优点。

2 模型检验

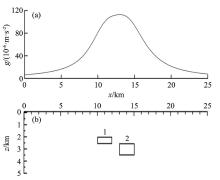
文中采用两个二度直立柱体的叠加异常进行数值检验。如图2b所示:模型体1长2 km, 上顶埋深2 km, 下底埋深2.5 km; 模型体2长2 km, 上顶埋深2.5 km, 下底埋深3.5 km; 两个模型体的剩余密度均为1.0 g/cm³。组合模型体产生的重力异常如图2a所示。

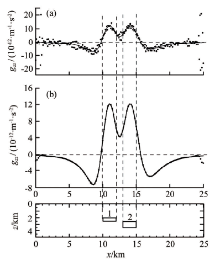
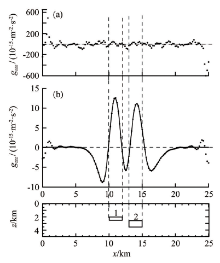
	Figure Option View Download New Window
	图2 模型重力异常及模型示意a— 模型体重力异常; b— 模型体示意

图3和图4是利用常规方法(直接FFT法)和迭代法得到的垂向二阶、三阶导数的对比结果。从图中可以看出:直接FFT法的导数值(图3a、4a)与理论值相比, 不仅存在明显的边界效应, 而且数据还存在着明显的波动性, 尤其垂向三阶导数(图4a)已无法识别出有效异常; 基于迭代法的导数换算得到的垂向二阶、三阶导数(图3b和图4b)与常规方法计算的导数(图3a和图4a)相比, 除了在边部有限数据产生吉布斯效应外, 其余数据点与理论值吻合较好。

上述模型检验结果表明, 直接FFT法的导数计算结果稳定性较差, 且导数阶次越高, 数据波动性越强, 而这也正是由于理论导数算子对高频成分的放大所引起的; 而迭代法不仅计算结果稳定性强, 且具有较强的保幅能力, 这也恰是迭代法的导数算子在低频段更能逼近理论导数因子而对高频成分更能有效压制的结果。

顺便指出的是, 随着异常导数阶次的增加, 其垂向导数异常的零值点与地质体边界位置的对应关系越好, 这种效果在图3和图4虚线所指示的地质体边界位置可以得到充分的说明。

	Figure Option View Download New Window
	图3 垂向二阶导数模型检验a— 直接FFT法; b— 迭代法

	Figure Option View Download New Window
	图4 垂向三阶导数模型检验a— 直接FFT法; b— 迭代法

3 实例应用

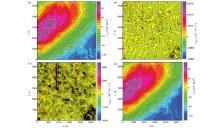
为了检验高阶导数迭代法对实际资料的处理效果, 在此选取东北地区某矿区的布格重力异常数据(图5a)进行垂向二阶导数处理。该地区重力数据共有109条测线, 每条测线111个测点, 网格间距大小为50 m× 50 m。

	Figure Option View Download New Window
	图5 实测重力异常的垂向二阶导数实验a— 原始重力异常; b— 直接FFT垂向二阶导数; c— 迭代法得到的垂向二阶导数; d— 图5c垂向二次积分得到的重力异常

从图5中可以看出, 直接FFT法得到的垂向二阶导数(图5b)结果稳定性极差, 基本不能反映出研究区异常的基本特征; 迭代法获得的垂向二阶导数(图5c)相对图5b不仅没有出现明显的振荡现象, 而且清晰地展示出了局部异常间的特征关系, 这则有利于研究区的异常定量解释及成矿远景预测。

为进一步验证迭代法得到的垂向二阶导数异常值的准确性, 对图5c利用FFT垂向积分算子进行二次积分, 得到的重力异常(图5d)与原始重力异常(图5a)除细微的局部异常(如图5a右下角)无法体现外, 异常的基本形态和幅值都获得了较大程度上的恢复。这表明位场高阶导数的波数域迭代法计算得到的导数异常结果不仅具有较好的稳定性, 而且具有较高的计算精度。

4 结论

文中从波数域的高阶导数响应因子的滤波特性出发, 结合迭代法逐步近似逼近的优点, 给出了解决位场高阶导数不稳定性的迭代算法, 同时证明了迭代法的收敛性和分析了迭代法的滤波特性。该方法可以利用迭代通式直接实现, 无需进行逐步迭代处理, 因此计算速度较快。同时方法原理简单, 易于实现, 有着较高的计算精度和较强的计算稳定性。该方法的提出, 为基于高阶导数的数字信号分析和欧拉反褶积等新兴方法提供了新的技术路线, 也为实际地质异常体的平面赋存状态及其边界位置精确确定等研究提供了新的思路。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Blakely R J. Potential theory in gravity and magnetic applications[M]. Cambridge University Press, 1995: 324-327. [本文引用:1]
[2]	骆燕, 李晓禄, 蔡文良, 等. 潮水地区航磁梯度初步分析[J]. 东华理工学院学报, 2007, 30(2): 164-170. [本文引用:1]
[3]	侯重初, 施志群. 实现重磁异常规格化总梯度的傅氏积分法[J]. 石油物探, 1986, 25(3): 75-86. [本文引用:1]
[4]	张凤旭, 孟令顺, 张凤琴, 等. 利用Hilbert变换计算重力归一化总梯度[J]. 地球物理学报, 2005, 48(3): 704-709. [本文引用:1]
[5]	Thompson D T. EUlDPH-A new technique for making computer assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47: 31-37. [本文引用:1]
[6]	Stavrev P, Reid A. Euler deconvolution of gravity anomalies from thick contact/fault structures with extended negative structural index[J]. Geophysics, 2010, 75(6): 151-158. [本文引用:1]
[7]	黄临平, 管志宁. 利用磁异常总梯度模确定磁源边界位置[J]. 华东地质学院学报, 1998, 21(2): 143-150. [本文引用:1]
[8]	张季生, 高锐, 李秋生, 等. 欧拉反褶积与解析信号相结合的位场反演方法[J]. 地球物理学报, 2011, 54(6): 1634-1641. [本文引用:1]
[9]	骆遥, 王明, 罗峰, 等. 重磁场二维希尔伯特变换——直接解析信号解释方法[J]. 地球物理学报, 2011, 54(7): 1912-1920. [本文引用:1]
[10]	刘保华, 张维冈, 孟恩. 重力异常垂向一阶导数的一种简便算法[J]. 青岛海洋大学学报, 1995, 25(2): 233-238. [本文引用:1]
[11]	汪炳柱. 用样条函数法求重力异常二阶垂向导数和向上延拓计算[J]. 石油地球物理勘探, 1996, 31(3): 415-422. [本文引用:1]
[12]	Lourenco J S, Morrison H F. Vector magnetic anomalies derived from measurements of single component of the field[J]. Geophysics, 1973, 38: 395-368. [本文引用:1]
[13]	Kevin L M, Juan H H. The complete gravity gradient tensor derived from the vertical component of gravity: A Fourier transform technique[J]. Journal of Applied Geophysics, 2001, 46: 159-l74. [本文引用:1]
[14]	姚长利, 管志宁, 黄卫宁. 位场转换的抽样分组法[J]. 石油地球物理勘探, 1997, 32(5): 696-702. [本文引用:1]
[15]	王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展[J]. 地球物理学进展, 2010, 25(1): 196-210. [本文引用:1]
[16]	Strakhov A V, Devitsyn V N. The reduction of observed values of a potential field to values at a constant level[J]. Akad. Nauk USSR Izv. Fizika Zemli (Physics of the Solid Earth), 1965, 4: 256-261. [本文引用:1]
[17]	徐世浙. 位场延拓的积分——迭代法[J]. 地球物理学报, 2006, 49(4): 1176-1182. [本文引用:1]
[18]	王彦国, 张凤旭, 王祝文, 等. 位场向下延拓的泰勒级数迭代法[J]. 石油地球物理勘探, 2011, 46(4): 657-662. [本文引用:1]

1995

0.0

... 在一定程度上可以划分不同深度和大小异常源产生的叠加异常,且导数的阶次越高,这种分辨能力就越强^[1,2] ...

2007

0.0

... 在一定程度上可以划分不同深度和大小异常源产生的叠加异常,且导数的阶次越高,这种分辨能力就越强^[1,2] ...

1986

0.0

... 同时导数换算也是位场数据处理和反演方法技术的核心运算,如:重力归一化总梯度法^[3,4]、欧拉反褶积法^[5,6]、解析信号法^[7,8,9],位场数据导数换算结果的好坏直接关系到这些反演方法的应用效果 ...

2005

0.0

1982

0.0

2010

0.0

1998

0.0

2011

0.0

2011

0.0

1995

0.0

... 空间域主要有最小二乘法、拉格朗日插值法^[10]、样条函数插值法^[11]等方法,但这类方法存在着计算精度低和计算速度慢的缺点 ...

1996

0.0

... 空间域主要有最小二乘法、拉格朗日插值法^[10]、样条函数插值法^[11]等方法,但这类方法存在着计算精度低和计算速度慢的缺点 ...

1973

0.0

... 波数域主要采用Fourier变换^[12,13],然而波数域中的导数响应因子本身具有高频放大作用,尤其求导阶次越高,数据因截断产生的吉布斯效应以及随机干扰的放大作用越强 ...

2001

0.0

1997

0.0

... 为了压制高阶导数的不稳定性,一般采取附加低通滤波器来达到压制高频干扰的目的^[14],如向上延拓、维纳滤波、正则化滤波等 ...

2010

0.0

... 目前人们普遍认为:采用向上延拓一定高度的方法来压制导数换算中的高频成分最为方便和实用^[15] ...

1965

0.0

... 基于此,在前人对迭代法的研究基础上^[16,17,18],结合高阶导数算子的滤波特性,提出了位场高阶导数的波数域迭代法,并对该方法进行了模型检验及实际应用 ...

2006

0.0

2011

0.0