稳定的二维TTI介质一阶qP波方程RSGFD数值模拟

引用本文

王小丹, 印兴耀, 杨富森. 稳定的二维TTI介质一阶qP波方程RSGFD数值模拟[J]. 物探与化探, 2016,40(1): 135-142.
WANG Xiao-Dan, YIN Xing-Yao, YANG Fu-Sen. RSGFD numerical simulation of stable 2D TTI first-order qP-wave equations[J]. Geophysical and Geochemical Exploration, 2016,40(1): 135-142.
Doi:10.11720/wtyht.2016.1.24 复制到剪切板

Permissions

稳定的二维TTI介质一阶qP波方程RSGFD数值模拟

王小丹, 印兴耀, 杨富森

中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

作者简介: 王小丹(1990-),女,硕士研究生,主要从事复杂介质地震波正、反演方面的研究工作。

收稿日期: 2015-02-09

基金: 国家自然科学基金(41204085); 国家重点基础研究发展计划(“973计划”)项目(2013CB228604)共同资助

摘要

相比于VTI介质qP波数值模拟方法,考虑倾角因素的TTI介质qP波数值模拟方法能够更加准确地描述各向异性介质中波场的传播特征。常规的声学近似方法往往会造成TTI介质中倾角急剧变化的区域出现数值不稳定,笔者首先引入一个各向异性控制参数,推导了稳定形式的TTI介质二阶qP波方程,保证qP波场的稳定传播;其次,通过引入波场的伪速度分量,推导了其等价的一阶应力—速度形式及相应的PML边界条件,并应用优化的旋转交错网格有限差分(RSGFD)方法实现了精确的数值模拟。数值结果表明:TTI介质一阶qP波方程能够稳定、有效地模拟qP波的运动学特征,利用优化的RSGFD方法可以得到精确的合成地震记录,同时可以相对地提高计算效率。

关键词: TTI介质; 一阶应力—速度; 数值模拟; 旋转交错网格有限差分; 控制参数; 稳定性; PML边界条件

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2016)01-0135-08 doi: 10.11720/wtyht.2016.1.24

RSGFD numerical simulation of stable 2D TTI first-order qP-wave equations

WANG Xiao-Dan, YIN Xing-Yao, YANG Fu-Sen

School of Geosciences,China University of Petroleum (East China),Qingdao 266580,China

Abstract

Compared with VTI qP-wave modeling,TTI qP-wave numerical simulation method which considers dip angle factor could be more accurate in describing the characteristics of wave-field propagation in real anisotropic media.Because of the rapid change of dip angle in TTI media,using the conventional acoustic approximated method may cause numerical instability.In this paper,the authors first derived the stable TTI second-order qP-wave equations by introducing an anisotropic control parameter to ensure the stability of qP-wave propagation.Then,the equivalent first-order stress-velocity forms were deduced through introducing the pseudo-velocity components of the wave-fields,and the corresponding PML boundary condition was given.Finally,the authors implemented accurate numerical simulation using the optimal rotated stagger-grid finite-difference (RSGFD) method.Numerical results demonstrate that TTI first-order qP-wave equations can describe the kinematics features of qP-wave effectively and stably,and the application of optimal RSGFD method can acquire accurate synthetic seismic recordings and enhance computational efficiency relatively.

Keyword: TTI media; first-order stress-velocity; numerical simulation; RSGFD; control parameter; stability; PML boundary condition

Show Figures

正演模拟是研究地震波场的形成机理以及传播规律的重要工具, 目前应用最广泛的是有限差分(FD)方法^{[1, 2, 3]}。研究表明, 地球介质广泛存在着各向异性, 对于盐丘侧翼等复杂地质构造, 基于VTI介质的数值模拟方法会带来运动学和动力学上的误差, 进而会影响成像结果的精度。实际地震勘探中仍以纵波资料为主, 因此, 研究TTI介质qP波方程及其数值模拟方法显得尤为重要。Alkhalifah^[4]从精确的VTI介质qP-qSV耦合频散关系出发, 利用声学假设近似, 推导了VTI介质四阶qP波方程。Zhang等^[5]从声学近似的VTI介质相速度出发, 将VTI介质qP波方程推广到TTI介质; Zhou等^[6]、Fletcher等^[7]基于声学近似的TTI介质频散关系, 分别推导了两种二阶耦合的TTI介质qP波方程。Fowler等^[8]于2010年给出了TI介质二阶耦合qP波方程的一般形式。

采用声学近似的各向异性介质qP波方程会产生一种固有的qSV人为干扰波(称为伪横波), 通过设置震源环的方法可以将其消除^[9]。同时, 在非均匀TTI介质中, 由于对称轴方向的急剧变化会造成波场传播的不稳定性现象。Fletcher等^[10]认为声学近似后的残余横波引起了数值不稳定, 因此引入一个非零的垂向剪切波速度来解决这一问题。Yoon等^[11]在对称轴急剧变化的区域, 令各向异性参数ε =δ , 以减弱数值不稳定性, 但这会修改介质参数, 从而导致较大误差。Zhang等^[12]通过引入自共轭旋转偏微分算子, 推导了稳定形式的TTI介质qP波方程, 但在数值离散过程中需要用特殊方法处理, 数值实现比较复杂。Zhan等^[13]推导了TTI介质近似解耦的qP波方程, 并在一定程度上解决了伪横波和不稳定性问题, 但其需要用伪谱法数值求解, 计算量大, 三维情况下不利于并行化实现。Chu等^[14]推导了TTI介质的近似纯qP波方程, 由于方程中含有四阶混合空间偏导数, 计算量大且复杂。程玖兵和康玮^[15]推导了动力学上qP波能量占优的TI介质伪纯模式qP波方程, 然而该方程计算量大和复杂各向异性介质条件下仍然存在横波干扰的问题不可忽略。

以上波动方程都是基于二阶或四阶偏微分算子, 采用常规矩形网格对二阶qP波方程进行差分离散时, 会引起较为严重的频散现象; 而利用交错网格有限差分(SGFD)技术可以有效减少数值频散, 提高计算精度^[16], 但其存在着对弹性模量进行插值处理的缺陷, 对于参数变化较大的非均匀各向异性介质, 会导致数值结果不准确。Gold等^[17]提出旋转交错网格有限差分(RSGFD)方法, 有效地克服了插值处理带来的误差问题, 但对于同样大小的网格单元, RSGFD法比常规SGFD需要更大的空间步长, 这往往会增加空间频散, Liu等^[18]基于模拟退火(SA)方法对有限差分系数进行优化, 提高了模拟精度。

为了解决声学近似带来的不稳定性问题和提高数值模拟精度, 笔者直接从TTI介质精确的qP-qSV波耦合频散关系出发, 通过引入一个各向异性控制参数, 推导了稳定的TTI介质二阶qP波方程。然后引入波场的伪速度分量, 推导了等价的一阶应力— 速度形式, 并给出了相应的PML边界控制方程。最后通过构造TTI介质一阶qP波方程的优化RSGFD格式, 实现TTI介质qP波场数值模拟, 得到了精确的合成地震记录。数值结果对比分析验证了方法的有效性和稳定性。

1 方法理论

1.1 稳定的二维TTI介质二阶qP波方程

从TTI介质Christoffel方程出发, 通过求解特征值问题, 可以得到qP、qSV、qSH三种不同的波型。对qSH波解耦后, 得到精确的TTI介质qP-qSV波耦合频散关系, 取其二维形式^[19]

$\begin{matrix} \begin{matrix} ω^{4} = [(v_{px}^{2} + v_{s 0}^{2}) h_{2} + (v_{p 0}^{2} + v_{s 0}^{2}) h_{1}] ω^{2} - v_{px}^{2} v_{s 0}^{2} h_{2}^{2} - \\ v_{px}^{2} v_{s 0}^{2} h_{1}^{2} + [v_{p 0}^{2} (v_{pn}^{2} - v_{px}^{2}) - v_{s 0}^{2} (v_{pn}^{2} + v_{px}^{2})] h_{1} h_{2}, \end{matrix} \end{matrix}$ (1)

式中:h₁= $\begin{matrix} k_{x}^{2} \end{matrix}$ sin²θ + $\begin{matrix} k_{z}^{2} \end{matrix}$ cos²θ +k_xk_zsin2θ ; h₂= $\begin{matrix} k_{x}^{2} \end{matrix}$ cos²θ + $\begin{matrix} k_{z}^{2} \end{matrix}$ sin²θ -k_xk_zsin2θ ; w是角频率; k_x, k_z是空间波数; θ 是对称轴倾角; v_p0、v_s0分别是沿对称面垂向的qP波和qSV波速度; v_p_x是对称面内的qP波速度, $\begin{matrix} v_{px}^{2} \end{matrix}$ = $\begin{matrix} v_{p 0}^{2} \end{matrix}$ (1+2ε ); v_p_n是qP波的NMO速度, $\begin{matrix} v_{pn}^{2} \end{matrix}$ = $\begin{matrix} v_{p 0}^{2} \end{matrix}$ (1+2δ ); ε 、δ 是Thomsen参数^[20]。

基于声学近似的TTI介质频散关系, Zhou等^[6]通过引入一个辅助函数q(ω , k_x, k_z), 推导了TTI介质二阶耦合qP波波动方程

$\begin{matrix} \{\begin{matrix} \partial^{2} p / \partial t^{2} = v_{pn}^{2} H_{2} (p + q) + v_{p 0}^{2} H_{1} p \\ \partial^{2} q / \partial t^{2} = (v_{px}^{2} - v_{pn}^{2}) H_{2} (p + q) \end{matrix} \end{matrix}$ (2)

式中:H₁=sin²θ ∂ ²/∂ x²+cos²θ ∂ ²/∂ z²+sin2θ ∂ ²/(∂ x∂ z); H₂=cos²θ ∂ ²/∂ x²+sin²θ ∂ ²/∂ z²-sin2θ ∂ ²/(∂ x∂ z)。

对于非均匀TTI介质, 用式(2)进行数值模拟时会导致波场传播在对称轴方向急剧变化区域出现不稳定现象。研究表明, 各向异性参数σ =(v_p0/v_s0)²(ε -δ )在很大程度上控制着qSV波的强度, 且其值大小不影响qP波的运动学和动力学特征^[19]。因此, 笔者引入各向异性控制参数σ 来保证qP波场的稳定传播, 同时有效地衰减伪横波能量。首先从精确的TTI介质频散关系式(1)出发, 引入包含各向异性参数σ 的辅助波场q(ω , k_x, k_z), 其满足

$\begin{matrix} \begin{matrix} q (x, k_{x}, k_{z}) = \\ \frac{(v_{px}^{2} - v_{pn}^{2}) h_{2} \times p (x, k_{x}, k_{z})}{2 σ ω^{2} + (v_{pn}^{2} - v_{px}^{2}) [h_{1} + (2 σ + 1) h_{2}]}, \end{matrix} \end{matrix}$ (3)

可以得到稳定形式的TTI介质二阶qP波方程

$\begin{matrix} \{\begin{matrix} \frac{\partial^{2} p}{\partial t^{2}} = v_{pn}^{2} H_{2} (p + q) + v_{p 0}^{2} H_{1} p - \frac{v_{px}^{2} - v_{pn}^{2}}{2 σ} H_{2} q \\ \frac{\partial^{2} q}{\partial t^{2}} = (v_{px}^{2} - v_{pn}^{2}) H_{2} (p + q) + \frac{v_{px}^{2} - v_{pn}^{2}}{2 σ} (H_{1} + H_{2}) q \end{matrix} \end{matrix}$ (4)

式中:p是伪应力场, q是为了简化计算而引入的辅助波场; H₁、H₂的定义同式(2)。若令σ =∞ , 即v_s₀=0时, 可得到声学近似的特殊情形, 即式(2)。

1.2 二维TTI介质一阶应力— 速度qP波方程

对于式(4)中的二阶偏微分方程, 采用常规矩形网格进行差分离散时, 会引起较为严重的频散现象, 同时其边界反射问题也难以有效解决, 因此可以研究等价的一阶应力— 速度形式波动方程。引入伪应力波场p和q的伪速度分量, 并沿着x、z方向进行分解, 令ρ ∂ u_p/∂ t=∂ p/∂ x; ρ ∂ ω _p/∂ t=∂ p/∂ z; ρ ∂ u_q/∂ t=∂ q/∂ x; ρ ∂ ω _q/∂ t=∂ q/∂ z。则式(4)可以转化为稳定的TTI介质一阶应力— 速度qP波方程

$\begin{matrix} \{\begin{matrix} \frac{\partial u_{p}}{\partial t} = \frac{1}{ρ} \frac{\partial p}{\partial x}, \frac{\partial ω_{p}}{\partial t} = \frac{1}{ρ} \frac{\partial p}{\partial z}, \\ \frac{\partial u_{q}}{\partial t} = \frac{1}{ρ} \frac{\partial q}{\partial x}, \frac{\partial ω_{q}}{\partial t} = \frac{1}{ρ} \frac{\partial q}{\partial z}, \\ \frac{\partial p}{\partial t} = ρ v_{pn}^{2} (T_{2} + G_{2}) + ρ v_{p 0}^{2} G_{1} + ρ \frac{v_{px}^{2} - v_{pn}^{2}}{2 σ} G_{2}, \\ \frac{\partial q}{\partial t} = ρ (v_{px}^{2} - v_{pn}^{2}) (T_{2} + G_{2}) + ρ \frac{v_{px}^{2} - v_{pn}^{2}}{2 σ} (T_{1} + G_{2}) 。 \end{matrix} \end{matrix}$ (5)

其中, 一阶偏微分算子T₁, T₂, G₁, G₂分别为

$\begin{matrix} \{\begin{matrix} T_{1} = si n^{2} θ \frac{\partial u_{q}}{\partial x} + co s^{2} θ \frac{\partial ω_{q}}{\partial z} + sinθcosθ (\frac{\partial u_{q}}{\partial z} + \frac{\partial ω_{q}}{\partial x}), \\ T_{2} = co s^{2} θ \frac{\partial u_{p}}{\partial x} + si n^{2} θ \frac{\partial ω_{p}}{\partial z} - sinθcosθ (\frac{\partial u_{p}}{\partial z} + \frac{\partial ω_{p}}{\partial x}), \\ G_{1} = si n^{2} θ \frac{\partial u_{p}}{\partial x} + co s^{2} θ \frac{\partial ω_{p}}{\partial z} + sinθcosθ (\frac{\partial u_{p}}{\partial z} + \frac{\partial ω_{p}}{\partial x}), \\ G_{2} = co s^{2} θ \frac{\partial u_{q}}{\partial x} + si n^{2} θ \frac{\partial ω_{q}}{\partial z} - sinθcosθ (\frac{\partial u_{p}}{\partial z} + \frac{\partial ω_{p}}{\partial x}) 。 \end{matrix} \end{matrix}$ (6)

式中:u_p、ω _p和u_q、ω _q分别表示波场p、q在x和z方向的伪速度分量。

当θ =0时, 式(5)退化为VTI介质情形。各向异性参数σ 控制着qSV波的波前形态, 且qSV波的振幅随着σ 值减小而减小^[19]。因此, 如果在整个计算区域选择一个足够小的恒定σ 值, 则能最大程度地衰减伪横波的干扰能量, 以此来保证qP波场的稳定传播。

2 数值实现

2.1 优化的旋转交错网格高阶有限差分格式

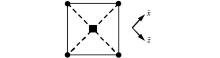
图1表示旋转交错网格的网格剖分示意, 物理分量和参数的具体分布位置如表1所示。各向异性

	Figure Option View Download New Window
	图1 RSGFD格式网格剖分示意

表1 RSGFD格式的参数分布位置

参数和倾角被定义在与应力相同的位置, 这样可以避免对其进行插值所带来的误差。

以方程(5)中波场p为例, 其关于坐标轴x和z方向的一阶空间偏导数的任意2N阶RSGFD算子可表示为^[17]

$\begin{matrix} \{\begin{matrix} \frac{\partial p (x, z, t)}{\partial x} = \frac{Δr}{2 Δx} [\frac{\partial p (x, z, t)}{\partial \dot{z}} + \frac{\partial p (x, z, t)}{\partial \dot{x}}], \\ \frac{\partial p (x, z, t)}{\partial z} = \frac{Δr}{2 Δz} [\frac{\partial p (x, z, t)}{\partial \dot{z}} - \frac{\partial p (x, z, t)}{\partial \dot{x}}] 。 \end{matrix} \end{matrix}$ (7)

其中:Δ x和Δ z分别是坐标轴x和z方向的空间步长; Δ r是对角线长度, Δ r= $\begin{matrix} \sqrt[]{{(Δ x)}^{2} + {(Δ z)}^{2}} \end{matrix}$ 。 $\begin{matrix} \frac{\partial}{\partial \tilde{x}} \end{matrix}$ 和 $\begin{matrix} \frac{\partial}{\partial \tilde{z}} \end{matrix}$ 分别表示沿对角线 $\begin{matrix} \tilde{x} \end{matrix}$ 和 $\begin{matrix} \tilde{z} \end{matrix}$ 方向的任意2N阶偏导数。设波场函数p(x, z, t)连续, 则有

$\begin{matrix} \{\begin{matrix} \frac{\partial p (x, z, t)}{\partial \dot{x}} = \frac{1}{Δr} \overset{N}{\sum_{n = 1}} C_{n}^{(N)} [p (x + \frac{2 n - 1}{2} Δx, z - \frac{2 n - 1}{2} Δz, t) - p (x - \frac{2 n - 1}{2} Δ x, z + \frac{2 n - 1}{2} Δz, t)], \\ \frac{\partial p (x, z, t)}{\partial \dot{z}} = \frac{1}{Δr} \overset{N}{\sum_{n = 1}} C_{n}^{(N)} [p (x + \frac{2 n - 1}{2} Δx, z + \frac{2 n - 1}{2} Δz, t) - p (x - \frac{2 n - 1}{2} Δx, z - \frac{2 n - 1}{2} Δz, t)] 。 \end{matrix} \end{matrix}$ (8)

式中: $\begin{matrix} C_{n}^{(N)} \end{matrix}$ 为一阶空间偏导算子的差分系数, 通常的求解方法是Taylor级数展开法。笔者基于模拟退火(SA)来优化RSGFD方法的差分系数, 以提高数值模拟的精度^[18]。将优化的差分系数代入式(8)中, 并联合式(7)和式(8), 则可得到任意2N阶精度的优化RSGFD格式。以式(5)中伪应力场p及其伪速度分量u_p和ω _p为例, 给出TTI介质一阶qP波方程的优化RSGFD格式

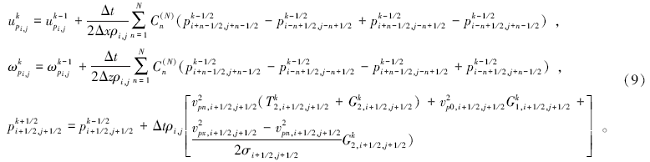
其中:i, j分别为空间离散点序号; k为时间离散点序号; Δ t为时间步长; 2N是差分阶数, $\begin{matrix} C_{n}^{(N)} \end{matrix}$ (n= 1, 2, …, N)为优化的差分系数。同理, 可以导出k时刻G₁, G₂, T₂的差分格式。

2.2 完全匹配层(PML)边界条件

为保证满意的边界吸收效果, 引入PML边界条件^[21], 依据PML的方程分裂思路, 导出适用于方程(5)的时间域完全匹配层控制方程

$\begin{matrix} \begin{matrix} \frac{\partial u_{p}}{\partial t} + d (x) u_{p} = \frac{1}{ρ} \frac{\partial p}{\partial x}; \frac{\partial ω_{p}}{\partial t} + d (z) ω_{p} = \frac{1}{ρ} \frac{\partial p}{\partial z}; p = p_{x} + p_{z}; \\ \frac{\partial p_{x}}{\partial t} + d (x) p_{x} = ρ v_{pn}^{2} [co s^{2} θ (\frac{\partial u_{p}}{\partial x} + \frac{\partial u_{q}}{\partial x}) - sinθcosθ (\frac{\partial ω_{p}}{\partial x} + \frac{\partial ω_{q}}{\partial x})] + ρ v_{p 0}^{2} [si n^{2} θ \frac{\partial u_{p}}{\partial x} + sinθcosθ \frac{\partial ω_{p}}{\partial x}] + \\ \frac{ρ (v_{px}^{2} - v_{pn}^{2})}{2 σ} [co s^{2} θ \frac{\partial u_{q}}{\partial x} - sinθcosθ \frac{\partial ω_{q}}{\partial x}]; \\ \frac{\partial p_{z}}{\partial t} + d (z) p_{z} = ρ v_{pn}^{2} [si n^{2} θ (\frac{\partial ω_{p}}{\partial z} + \frac{\partial ω_{q}}{\partial z}) - sinθcosθ (\frac{\partial u_{p}}{\partial z} + \frac{\partial u_{q}}{\partial z})] + ρ v_{p 0}^{2} [co s^{2} θ \frac{\partial ω_{p}}{\partial z} + sinθcosθ \frac{\partial u_{p}}{\partial z}] + \\ \frac{ρ (v_{px}^{2} - v_{pn}^{2})}{2 σ} [si n^{2} θ \frac{\partial ω_{q}}{\partial z} - sinθcosθ \frac{\partial u_{q}}{\partial z}] 。 \end{matrix} \end{matrix}$

式中:p为伪应力场; u_p和ω _p为p的速度分量; p_x和p_z为波场p在x、z方向的分裂算子; d(x)和d(z)为x、z方向的阻尼因子, 可表示为

$\begin{matrix} \begin{matrix} d (x) = \{\begin{matrix} - \frac{v_{\max} lnα}{L} [a \frac{x_{i}}{L} + b {(\frac{x_{i}}{L})}^{2}], \\ 0; \end{matrix} \\ d (z) = \{\begin{matrix} - \frac{v_{\max} lnα}{L} [a \frac{z_{i}}{L} + b {(\frac{z_{i}}{L})}^{2}] 匹配层区域, \\ 0 非匹配层区域。 \end{matrix} \end{matrix} \end{matrix}$

式中:x_i和z_i分别为匹配层区域与内部区域界面的横向和纵向距离; v_max为模型区域内的最大速度值; L为匹配层宽度; α =10^-6; 系数a=0.25, b=0.75。

3 模型试算

3.1 均匀TTI介质模型

设计一个均匀TTI介质模型, 其参数为:v_p0=2 500 m/s, ε =0.24, δ =0.10, θ =45° , ρ =1 g/cm³; 网格大小201× 201, 网格尺寸Δ x=Δ z=10 m, 采样间隔Δ t=1 ms; 选用主频为25 Hz的雷克子波震源, 置于模型中心处。采用空间十阶和时间二阶的优化RSGFD方法进行正演模拟, 分别得到VTI介质弹性波(θ =0° )、VTI介质一阶qP波(θ =0° )、TTI介质一阶qP波正演模拟在300 ms时刻的波场快照, 如图2所示。由图2a和2b可知, 外层传播较快的均为qP波, 两者的波阵面具有很好的一致性; 图2a中内层传播较慢的是qSV波, 而图2b中内层的菱状波形是声近似特殊情况下产生的伪横波(箭头所示)。由图2c可知, 在激发震源周围设置小范围的椭圆各向异性区域(即震源环)后, 震源处产生的伪横波得到了很好的压制, 则能保证仅含有qP波的波场传播。同样, 图2d是设置震源环后的TTI介质qP波波场快照。由此可知, 应用方程(5)能够比较准确地模拟VTI和TTI介质中qP波的运动学特征。

	Figure Option View Download New Window
	图2 t=300 ms时刻的波场快照对比a— VTI弹性波正演的垂直应力分量; b— 设置震源环前的VTI介质qP波正演的p波场; c— 设置震源环后的VTI介质qP波正演的p波场; d— 设置震源环后的TTI介质qP波正演的p波场

为更好地验证优化RSGFD方法的精确性, 首先将震源主频设置为30 Hz, 其他模拟参数同图2。然后分别利用不同空间差分阶数的常规RSGFD和优化RSGFD方法进行模型试算, 得到300 ms时刻的TTI介质qP波波场快照, 如图3所示。由图可知, 对于相同的空间差分阶数, 优化方法数值频散更弱, 模拟精度更高。

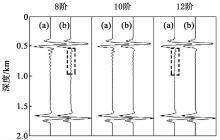
	Figure Option View Download New Window
	图3 t=300 ms时刻不同空间差分阶数的常规RSGFD和优化RSGFD方法得到的波场快照对比a— 常规RSGFD8阶; b— 常规RSGFD10阶; c— 常规RSGFD12阶; d— 优化RSGFD8阶; e— 优化RSGFD10阶; f— 优化RSGFD12阶

图4是从图3中地面位置600 m处抽取的单道波形对比结果, 同样可以看出, 优化方法的精度更高, 而且8阶优化方法与12阶常规方法的数值频散相当, 这表明用相对低阶的优化方法就能达到高阶常规方法的模拟精度(如图4中虚线框区域所示)。

	Figure Option View Download New Window
	图4 不同空间差分阶数的常规RSGFD(a)与优化RSGFD(b)方法的单道波形对比

表2显示了不同空间差分阶数对应的常规RSGFD和优化RSGFD方法的计算时间对比结果(正演模拟参数同图3, 记录总时间为3.0 s)。由表2可知, 相同空间差分阶数条件下, 优化方法的计算时间略低于常规方法, 前者相对于后者效率提高了约4%。而同一种方法的计算时间随着空间差分阶数的增大而增加, 因此, 对于给定的模拟精度, 利用低阶的优化方法可以大大地提高计算效率。以8阶优化方法和12阶常规方法为例, 两者的精度相当, 但是前者相对于后者效率提高了约29.8%。

表2 不同空间差分阶数的常规RSGFD和优化RSGFD方法的计算时间对比s

图5为应用PML边界条件后的qP波波场快照(正演模拟参数和差分格式与图2相同), 从左至右的时间依次为300、400、500、600、700 ms。由图可知, 在进行TTI介质qP波正演模拟时, 利用本文推导的PML边界条件能获得理想的边界吸收效果。

	Figure Option View Download New Window
	图5 应用PML边界条件后的qP波波场快照

3.2 TTI介质层状模型

图6a显示了一个网格大小为301× 301的TTI介质层状模型及其各向异性参数, 密度ρ =1 g/cm³, 网格间距为10 m× 10 m, 采用空间十阶和时间二阶的优化RSGFD方法进行正演模拟。正演模拟的观测系统为:选用主频为25 Hz的雷克子波震源, 置于模型x=1 500 m, z=10 m处, 采用中间放炮, 两边接收的方式, 共301道, 道间距为10 m, 采样间隔△ t=1.0 ms, 记录时间为1.5 s。

	Figure Option View Download New Window
	图6 TTI介质层状模型及t=580ms时刻的波场快照a— 各向异性参数; b— VTI方法; c— TTI方法

图6b和6c分别为VTI方法和TTI方法得到的t=580 ms时刻的波场快照。图7分别显示了各向同性声波方程(图7a)、VTI介质一阶qP波方程(图7b)、TTI介质一阶qP波方程(图7c)正演模拟得到的单炮地震记录。由图6和图7可知, TTI介质的倾角因素会造成波前面形态发生扭曲, 同时各向异性因素会改变旅行时等运动学特征, 如图6中深度1 000~1 500 m范围和图7中时间700~1 100 ms范围的虚线框区域所示。

	Figure Option View Download New Window
	图7 合成地震记录a— 各向同性声波方程正演; b— VTI一阶qP波方程正演; c— TTI一阶qP波方程正演

为了更清晰地对比波场特征的变化, 从图7a、7b、7c中小偏移距处(1 200 m)和大偏移距处(200 m)分别抽取一条地震道, 得到如图8所示的单道波形对比图, 主要对比两个反射层位的波形。由图8中红细虚线和实线可知, 相比于各向同性声波正演模拟结果, 考虑各向异性因素(参数ε 和δ )的影响后, 各层的反射旅行时和波形振幅均发生变化, 特别是大偏移距处, 这种影响更明显, 且往往造成旅行时和振幅减小(图8b中实线)。同时对比图8中VTI和TTI伪声波模拟可知, 模型中第二层受到TTI介质的倾角影响后, 振幅和旅行时等波场特征会进一步改变。因此, 在针对实际资料中大倾角各向异性构造处理时, 必须要考虑到TI介质的倾角因素。

	Figure Option View Download New Window
	图8 单道波形对比a— 小偏移距; b— 大偏移距

3.3 TTI介质逆掩断层模型

最后, 利用空间十阶和时间二阶的优化RSGFD方法对TTI介质逆掩断层模型进行正演模拟, 模型的各向异性参数v_p0、ε 、δ 及倾角θ , 如图9a和9b所示, 密度ρ =1 g/cm³; 模型网格大小为401× 401, 网格间距为10 m× 10 m。正演模拟的观测系统为:选用主频为30 Hz的雷克子波震源, 置于x=2 000 m, z=10 m处, 采用中间放炮, 两边接收的方式, 共401道, 道间距为10 m, 采样间隔△ t=1.0 ms, 记录时间为3.0 s。图9c和9d分别是应用稳定的TTI介质一阶qP波方程式(5)(设置控制参数σ =0.4)和不稳定的TTI介质qP波方程^[6]得到的700 ms时刻的波场快照。对比两者可知, 倾角变化引起的波场传播不稳定严重地干扰了有效的qP波能量, 不利于得到准确的qP波合成地震记录。

	Figure Option View Download New Window
	图9 TTI逆掩断层模型参数及t=700 ms时刻的qP波波场快照a— v_p0, ε , δ ; b— θ ; c— 不稳定方程; d— 稳定方程

图10是应用TTI一阶qP波稳定方程得到的单炮地震记录, 图10a和10c分别对应常规RSGFD方法和优化RSGFD方法, 图10b和10d分别为虚线框区域相应的局部放大结果。对比图10b和10d可知, 常规RSGFD方法得到的地震记录中由于频散严重, 使得同相轴发生扰动, 同时造成下方的同相轴变得模糊, 连续性不好(图10b中箭头所示); 而优化RSGFD方法得到的地震记录中同相轴更加清晰, 连续性更好。因此, 在相同的数值离散条件下, 利用优化方法能够有效地压制数值频散, 提高模拟精度。

	Figure Option View Download New Window
	图10 合成的qP波地震记录a— 常规RSGFD方法; b— a中虚线框区域局部放大; c— 优化RSGFD方法; d— c中虚线框区域局部放大

4 结论

基于精确的TTI介质qP-qSV耦合频散关系, 引入一个包含各向异性参数σ 的辅助波场, 推导了稳定形式的TTI介质二阶qP波方程; 然后通过引入波场的伪速度分量, 将其转换为等价的一阶应力— 速度形式, 并推导了相应的PML边界条件; 最后利用优化的RSGFD方法实现了精确的qP波数值模拟。

数值结果表明, TTI介质一阶qP波方程能够有效地模拟qP波的运动学特征, 有利研究各向异性介质中qP波的传播规律, 并为后续的各向异性资料处理和解释提供理论基础。相比于常规RSGFD方法, 优化RSGFD方法压制频散效果更好, 模拟精度更高; 并且对于给定的模拟精度, 利用优化RSGFD方法还可以相对地提高计算效率。在波场数值模拟过程中, 利用本文推导的TTI介质一阶qP波方程相应的PML边界条件可以实现对边界反射能量的有效吸收。

其次, 模型的波场特征分析表明了地球介质的各向异性因素会对地震记录的旅行时和振幅等波场特征产生一定影响, 特别是远偏移距处这种影响更加明显, 进而还会影响偏移成像的精度。因此, 在针对实际生产中大偏移距、宽方位地震资料的处理时, 各向异性因素越来越不能忽略。最后, 逆掩断层模型的测试结果表明, 引入控制参数σ 可以实现倾角突变的TTI介质中qP波场的稳定传播, 进而利用优化RSGFD方法得到了精确的qP波合成地震记录。利用稳定的TTI介质一阶qP波有限差分算子进行精确的偏移成像将是下一步的研究方向。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李振春. 地震叠前成像理论与方法[M]. 东营: 中国石油大学出版社, 2011: 24-39. [本文引用:1]
[2]	裴正林. 三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油大学学报: 自然科学版, 2004, 28(5): 23-29. [本文引用:1]
[3]	何兵寿, 张会星. VTI介质中准P波方程的数值解法[J]. 煤炭学报, 2006, 31(4): 446-450. [本文引用:1]
[4]	Alkhalifah T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. [本文引用:1]
[5]	Zhang L B, Rector J W, Hoversten G M. An acoustic wave equation for modeling in tilted TI media[J]. SEG, 2003. [本文引用:1]
[6]	Zhou H B, Zhang G Q, Bloor R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]//Expand ed Abstracts of 76^th SEG Annual Internet Meeting, 2006: 194-198. [本文引用:3]
[7]	Fletcher R, Du X, Fowler P J. A new pseudo-acoustic wave equation for TI media[C]//Expand ed Abstracts of 78^th SEG Annual Internet Meeting, 2008: 2082-3086. [本文引用:1]
[8]	Fowler P J, Du X, Fletcher R P. Coupled equations for reverse time migration in transversely isotropic media[J]. Geophysics, 2010, 75(1): S11-S22. [本文引用:1]
[9]	Grechka V, Zhang L, Rector J W. Shear waves in acoustic anisotropic media[J]. Geophysics, 2004, 69(2): 576-582. [本文引用:1]
[10]	Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic(TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. [本文引用:1]
[11]	Yoon K, Sang S, Jean J, et al. Stability and speedup issues in TTI RTM implementation[C]//Expand ed Abstracts of 80^th SEG Annual Internet Meeting, 2010: 3221-3225. [本文引用:1]
[12]	Zhang Y, Zhang H Z, Zhang G Q. A Stable TTI Reverse time migration and its implementation[J]. Geophysics, 2011, 76: WA3-WA11. [本文引用:1]
[13]	Zhan G, Pestana R C, Stoffa P L. An acoustic wave equation for pure P wave in 2D TTI media[C]//Expand ed Abstracts of 81^st SEG Annual Internet Meeting, 2011: 168-173. [本文引用:1]
[14]	Chu C L, Macy B K, Anno P D. An accurate and stable wave equation for pure acoustic TTI modeling[C]//Expand ed Abstracts of 81^st SEG Annual Internet Meeting, 2011: 179-184. [本文引用:1]
[15]	程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述I: 伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10): 3474-3486. [本文引用:1]
[16]	Madariage R. Dynamics of an expand ing circular fault[J]. Bulletin of the Seismological Society of American, 1976, 66: 639-666. [本文引用:1]
[17]	Gold N, Shapiro S A, Burr E, et al. Modeling of high contrasts in elastic media using a modified finite difference scheme[C]//Expand ed Abstracts of 67^th SEG Annual Internet Meeting, 1997: 1850-1853. [本文引用:2]
[18]	Liu B, Yin X Y, Yang F Y. Optimization of rotated staggered-grid scheme for seismic forward modeling[J]. SEG Technical Program Expand ed Abstracts, 2014: 3308-3312. [本文引用:2]
[19]	Tsvankin I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media[J]. Elsevier Science, 2001: 1-60. [本文引用:3]
[20]	Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. [本文引用:1]
[21]	Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-220. [本文引用:1]

2011

0.0

... 正演模拟是研究地震波场的形成机理以及传播规律的重要工具,目前应用最广泛的是有限差分(FD)方法^[1,2,3] ...

2004

0.0

裴正林. 三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油大学学报: 自然科学版, 2004, 28(5): 23-29.

摘　要：三维数值模拟是研究各向异性介质中复杂弹性波波场特征和传播规律的重要手段.根据Taylor展开式,推导出了交错网格一阶空间导数的任意偶数阶精度有限差分近似式和相应的差分系数计算式,给出了三维各向异性介质中弹性波一阶双曲型应力-速度方程交错网格任意偶数阶精度差分格式和稳定性条件,并推导出了三维各向异性介质PML法吸收层边界条件公式和相应的交错网格差分格式.对方位各向异性介质模型和正交各向异性介质模型中弹性波的传播进行的三维数值模拟结果表明,弹性波在三维各向异性介质中传播时存在拟P波、拟SV波和拟SH波,并出现横波分裂、横波分裂盲区、波面三分叉等特殊现象,另外,弹性波场在空间是变化的,其拟P波、拟SV波和拟SH波的耦合关系比较复杂.

... 正演模拟是研究地震波场的形成机理以及传播规律的重要工具,目前应用最广泛的是有限差分(FD)方法^[1,2,3] ...

2006

0.0

何兵寿, 张会星. VTI介质中准P波方程的数值解法[J]. 煤炭学报, 2006, 31(4): 446-450.

To overcome the shortage of normal elastic wave forward modeling result，the numerical solution of quasi-P wave equations in transversely isotropic media with a vertical symmetry axis(VTI) was studied. Based on the quasi-P wave equations in VTI media，a high-order finite-difference scheme was derived by using an evenorder accurate difference operator，the stability conditions and the absorbing boundary conditions were also provided. In order to improve the precision of numerical solution，a flux-corrected transport technique was introduced to suppress the numerical dispersion，and by placing the source in isotropic media the error solution of quasi-P wave equations was eliminated completely. Using all above techniques the mathematical model for quasi-P wave equations simulation was established.

为克服常规弹性波动方程正演结果的局限，研究了具有垂直对称轴的横向各向同性（VTI）介质中准P波方程的数值解法.首先从VTI介质中准P波方程出发，采用任意偶数阶精度有限差分算子构造了准P波方程数值求解的高阶有限差分格式，给出了其稳定性条件和边界条件的计算方法.为提高数值求解精度，引入通量校正算法压制数值频散，将震源置于各向同性介质内以消除准P波方程的误差解，在此基础上建立了VTI介质中准P波方程正演的数学模型.

... 正演模拟是研究地震波场的形成机理以及传播规律的重要工具,目前应用最广泛的是有限差分(FD)方法^[1,2,3] ...

2000

0.0

... Alkhalifah^[4]从精确的VTI介质qP-qSV耦合频散关系出发,利用声学假设近似,推导了VTI介质四阶qP波方程 ...

2003

0.0

... Zhang等^[5]从声学近似的VTI介质相速度出发,将VTI介质qP波方程推广到TTI介质 ...

2006

0.0

... Zhou等^[6]、Fletcher等^[7]基于声学近似的TTI介质频散关系,分别推导了两种二阶耦合的TTI介质qP波方程 ...

... 基于声学近似的TTI介质频散关系,Zhou等^[6]通过引入一个辅助函数q(#cod#x003c9 ...

... 4)和不稳定的TTI介质qP波方程^[6]得到的700 ms时刻的波场快照 ...

2008

0.0

... Zhou等^[6]、Fletcher等^[7]基于声学近似的TTI介质频散关系,分别推导了两种二阶耦合的TTI介质qP波方程 ...

2010

0.0

... Fowler等^[8]于2010年给出了TI介质二阶耦合qP波方程的一般形式 ...

2004

0.0

... 采用声学近似的各向异性介质qP波方程会产生一种固有的qSV人为干扰波(称为伪横波),通过设置震源环的方法可以将其消除^[9] ...

2009

0.0

... Fletcher等^[10]认为声学近似后的残余横波引起了数值不稳定,因此引入一个非零的垂向剪切波速度来解决这一问题 ...

2010

0.0

... Yoon等^[11]在对称轴急剧变化的区域,令各向异性参数#cod#x003b5 ...

2011

0.0

... Zhang等^[12]通过引入自共轭旋转偏微分算子,推导了稳定形式的TTI介质qP波方程,但在数值离散过程中需要用特殊方法处理,数值实现比较复杂 ...

2011

0.0

... Zhan等^[13]推导了TTI介质近似解耦的qP波方程,并在一定程度上解决了伪横波和不稳定性问题,但其需要用伪谱法数值求解,计算量大,三维情况下不利于并行化实现 ...

2011

0.0

... Chu等^[14]推导了TTI介质的近似纯qP波方程,由于方程中含有四阶混合空间偏导数,计算量大且复杂 ...

2013

0.0

程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述I: 伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10): 3474-3486.

地球介质相对于地震波波长尺度的定向非均匀性会导致波速的各向异性,进而影响地震波场的运动学与动力学特征.各向异性弹性波动方程是描述该类介质波场传播的基本工具,在正演模拟、偏移成像与参数反演中起着关键作用.为了面向实际应用构建灵活、简便的各向异性波场传播算子,人们一直在寻求简化的各向异性波动方程.本文借鉴各向异性弹性波波型分离思想,通过对平面波形式的弹性波方程(即Christoffel方程)实施一种代表向波矢量方向投影的相似变换,推导出了一种适应任意各向异性介质、运动学上与原始弹性波方程完全等价,在动力学上突出qP波的新方程,即qP波伪纯模式波动方程.文中以横向各向同性(TI)介质为例,给出了相应的qP波伪纯模式波动方程及其声学与各向同性近似,并在此基础上开展了正演模拟和逆时偏移试验,展示了这种描述各向异性波场传播的新方程的特点与优势.

... 程玖兵和康玮^[15]推导了动力学上qP波能量占优的TI介质伪纯模式qP波方程,然而该方程计算量大和复杂各向异性介质条件下仍然存在横波干扰的问题不可忽略 ...

1976

0.0

... 而利用交错网格有限差分(SGFD)技术可以有效减少数值频散,提高计算精度^[16],但其存在着对弹性模量进行插值处理的缺陷,对于参数变化较大的非均匀各向异性介质,会导致数值结果不准确 ...

1997

0.0

... Gold等^[17]提出旋转交错网格有限差分(RSGFD)方法,有效地克服了插值处理带来的误差问题,但对于同样大小的网格单元,RSGFD法比常规SGFD需要更大的空间步长,这往往会增加空间频散,Liu等^[18]基于模拟退火(SA)方法对有限差分系数进行优化,提高了模拟精度 ...

... 以方程(5)中波场p为例,其关于坐标轴x和z方向的一阶空间偏导数的任意2N阶RSGFD算子可表示为^[17] ...

2014

0.0

... 笔者基于模拟退火(SA)来优化RSGFD方法的差分系数,以提高数值模拟的精度^[18] ...

2001

0.0

... 对qSH波解耦后,得到精确的TTI介质qP-qSV波耦合频散关系,取其二维形式^[19] ...

... )在很大程度上控制着qSV波的强度,且其值大小不影响qP波的运动学和动力学特征^[19] ...

... 值减小而减小^[19] ...

1986

0.0

... 是Thomsen参数^[20] ...

1994

0.0

... 2 完全匹配层(PML)边界条件为保证满意的边界吸收效果,引入PML边界条件^[21],依据PML的方程分裂思路,导出适用于方程(5)的时间域完全匹配层控制方程 ...