重力梯度张量分量转换处理误差研究

引用本文

舒晴, 张文志, 周坚鑫, 尹航, 高维. 重力梯度张量分量转换处理误差研究[J]. 物探与化探, 2016,40(1): 111-116.
SHU Qing, ZHANG Wen-Zhi, ZHOU Jian-Xin, YIN Hang, GAO Wei. Error Study on gravity gradient tensor components transformation[J]. Geophysical and Geochemical Exploration, 2016,40(1): 111-116.
Doi:10.11720/wtyht.2016.1.20 复制到剪切板

Permissions

重力梯度张量分量转换处理误差研究

舒晴^1,², 张文志², 周坚鑫², 尹航², 高维²

1.吉林大学地球探测科学与技术学院,吉林长春 130021

2.中国国土资源航空物探遥感中心,北京 100083

作者简介: 舒晴(1979-),男,高级工程师,吉林大学在读博士,长期从事航空地球物理方法技术研究与地质解释工作。

收稿日期: 2015-06-30

基金: 国家“十二五”863计划主题项目课题(2011AA060501)、地质矿产调查评价项目(1212011087013)

摘要

从 U_xy分量不同数据长度重力梯度张量分量转换处理模型实验入手,通过频谱畸变和空间域转换误差对比分析,发现转换处理公式中频率域奇点是转换误差产生的根源,增加数据长度、提高频率分辨率可减小转换处理误差、改善转换处理效果。

关键词: 重力梯度张量; 转换处理; 误差分析; 频谱畸变; 奇点

中图分类号:P632 文献标志码:A 文章编号:1000-8918(2016)01-0111-06 doi: 10.11720/wtyht.2016.1.20

Error Study on gravity gradient tensor components transformation

SHU Qing^1,², ZHANG Wen-Zhi², ZHOU Jian-Xin², YIN Hang², GAO Wei²

1.College of Geoexploration Science and Technology, Jilin University,Changchun 130021,China

2.China Aero Geophysics Survey and Remote Sensing Center for Land and Resources,Beijing 100083,China

Abstract

Based on the gravity gradient transformation model experiments for different data length,the frequency singular points in the transformation expressions was found to be the error source by spectrum and anomaly distortion analysis.The transformation error will decrease and the result will be better as the frequency resolution improvement with the data length increasing.

Keyword: gravity gradient tensor; transformation; error analysis; spectrum distortion; singular point

Show Figures

对于部分张量重力梯度测量^{[1, 2, 3, 4, 5, 6, 7]}而言, 以重力位为纽带^[8], 利用重力梯度张量分量之间的内在联系, 通过频率域转换得到其他张量分量, 从而获取更加多元的重力梯度异常信息, 是简化地质解释、精化推断结果的重要手段。同时, 由于重力梯度张量分量转换处理在频率域中进行, 实际应用中针对有限长离散信号, 因此, 转换处理效果会受到数字信号处理方法技术的影响。笔者首先给出了重力梯度张量分量转换处理公式, 简要分析了矩形棱柱体模型重力梯度张量异常的空间域和频率域特征, 以U_xy分量转换处理为例, 从数字信号处理角度, 分析了数据长度(相当于测线长度)对转换处理效果的影响, 并对误差产生的原因进行了深入剖析。

1 重力梯度张量分量频率域转换公式

对于平面数据, 重力梯度张量各分量与重力位二维傅里叶变换关系^{[9, 10]}

$\begin{matrix} \begin{matrix} {\tilde{U}}_{xx} (k_{x}, k_{y}, z) = - k_{x}^{2} \tilde{U} (k_{x}, k_{y}, z), \\ {\tilde{U}}_{xy} (k_{x}, k_{y}, z) = - k_{x} k_{y} \tilde{U} (k_{x}, k_{y}, z), \\ {\tilde{U}}_{xz} (k_{x}, k_{y}, z) = i k_{x} \sqrt[]{k_{x}^{2} + k_{y}^{2}} \tilde{U} (k_{x}, k_{y}, z), \\ {\tilde{U}}_{yy} (k_{x}, k_{y}, z) = - k_{y}^{2} \tilde{U} (k_{x}, k_{y}, z), \\ {\tilde{U}}_{yz} (k_{x}, k_{y}, z) = i k_{y} \sqrt[]{k_{x}^{2} + k_{y}^{2}} \tilde{U} (k_{x}, k_{y}, z), \\ {\tilde{U}}_{zz} (k_{x}, k_{y}, z) = (k_{x}^{2} + k_{y}^{2}) \tilde{U} (k_{x}, k_{y}, z) 。 \end{matrix} \end{matrix}$ (1)

显而易见, 只要获得某一高度平面的任意分量数据, 便可以重力位为纽带, 通过重力梯度张量分量频率域变换得到其他分量的空间域结果。假设在高度z=z₀平面测量结果为U_xy, 通过二维傅立叶变换可得其二维频谱U_xy(k_x, k_y, z₀), 结合式(1), 可得基于 $\begin{matrix} {\dot{U}}_{xy} \end{matrix}$ (k_x, k_y, z₀)的重力梯度张量分量转换公式为

$\begin{matrix} \begin{matrix} U_{xx} (x, y, z_{0}) = F_{x, y}^{- 1} [\frac{k_{x}}{k_{y}} {\tilde{U}}_{xy} (k_{x}, k_{y}, z_{0})], \\ U_{xz} (x, y, z_{0}) = F_{x, y}^{- 1} [\frac{\sqrt[]{k_{x}^{2} + k_{y}^{2}}}{i k_{y}} {\tilde{U}}_{xy} (k_{x}, k_{y}, z_{0})], \\ U_{yy} (x, y, z_{0}) = F_{x, y}^{- 1} [\frac{k_{y}}{k_{x}} {\tilde{U}}_{xy} (k_{x}, k_{y}, z_{0})], \\ U_{yz} (x, y, z_{0}) = F_{x, y}^{- 1} [\frac{\sqrt[]{k_{x}^{2} + k_{y}^{2}}}{i k_{x}} {\tilde{U}}_{xy} (k_{x}, k_{y}, z_{0})], \\ U_{zz} (x, y, z_{0}) = F_{x, y}^{- 1} [\frac{k_{x}^{2} + k_{y}^{2}}{k_{x} k_{y}} {\tilde{U}}_{xy} (k_{x}, k_{y}, z_{0})] 。 \end{matrix} \end{matrix}$ (2)

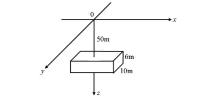
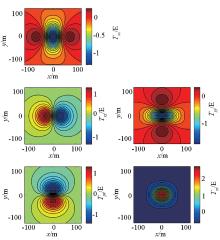
如式(2)所示, 通过已知分量的二维频谱 $\begin{matrix} {\dot{U}}_{xy} \end{matrix}$ (k_x, k_y, z₀), 乘以相应的频率域转换系数, 再进行傅里叶逆变换便可得到其他张量分量的空间域结果。

2 重力梯度张量异常空间及频谱特征

图1所示矩形棱柱体模型, 其重力梯度张量异常空间域特征及频谱特性分别如图2、3所示。

	Figure Option View Download New Window
	图1 地下半空间矩形棱柱体模型示意

	Figure Option View Download New Window
	图2 模型重力梯度张量异常平面等值线

	Figure Option View Download New Window
	图3 模型重力梯度张量异常二维振幅谱

如图所示, 模型重力梯度张量异常不仅在空间上呈对称分布, 其振幅谱也有类似于空间域的对称分布特征。从图3可以看出, 模型重力梯度异常在x、y两个方向上, 信号能量主要集中在0.0 005~0.01 cyc/m(周每米)范围内, 当频率高于0.02 cyc/m时, 异常信号能量已经很弱, 可忽略不计。

3 数据长度对转换处理效果的影响

在频率域^[11], 信号的采样频率必须高于二倍信号最高频率(f_s> 2f_h)才不会出现混叠现象。对于图1所示模型而言, 其重力梯度张量异常信号最高频率f_h≈ 0.02 cyc/m, 根据抽样定理, 采样频率必须满足f_s> 0.04 cyc/m, 对应空间采样间隔Δ < 25 m, 即观测平面网格距小于25 m× 25 m时, 测量(或正演)结果才能不失真的保留重力梯度张量异常信息。

对于离散傅里叶变换, 空间采样间隔Δ 决定了频率域截止频率f_c, 当采样间隔Δ (相当于点距)固定, 频带宽度一定时, 频谱分辨率(F₀=1/L)取决于数据长度(L=(N-1)× Δ )。当空间采样率 (或数据网格距)固定, 信号频带宽度一定时, 分析数据长度对转换效果的影响, 通俗的讲, 就是在模型上方不同范围内取值进行转换处理并分析其对最终结果的影响。笔者以直立矩形棱柱体模型U_xy分量转换处理为例进行分析。

对图1所示模型, 为保证信号不失真, 选取网格距为10 m× 10 m, 对应频率截止频率f_c> 0.05 cyc/m。为研究数据长度对转换结果的影响, 选取三组数据进行模型实验, 对应的数据长度、数据范围及频率分辨率为

1)N=51, x、y范围:-250~250 m, 分辨率F₀_x=F₀_y=0.002 cyc/m;

2)N=101, x、y范围:-500~500 m, 分辨率F₀_x=F₀_y=0.001 cyc/m;

3)N=401, x、y范围:-2000~2000 m, 分辨率F₀_x=F₀_y=0.00 025 cyc/m。

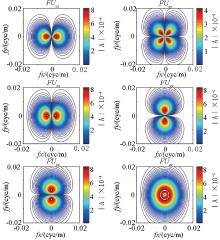
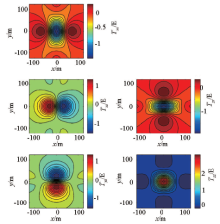
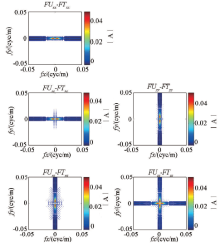
图4、5、6为转换处理结果, 对于以上长度不同的三组数据, 通过转换处理均能有效计算出其他张量分量, 各分量异常特征、位置及分布范围与模型正演计算结果(图2)基本一致; 当N=51时, 由于频率分辨率较低, 频点数较少, 异常等值线不光滑, 存在抖动; 随着数据长度增加和频率分辨率的提高转换处理效果改善明显; 当N=401时, 转换结果基本与理论值吻合。

	Figure Option View Download New Window
	图4 由U_xy分量转换重力梯度张量其它分量结果(N=51)

	Figure Option View Download New Window
	图5 由U_xy分量转换重力梯度张量其它分量结果(N=101)

	Figure Option View Download New Window
	图6 由U_xy分量转换重力梯度张量其它分量结果(N=401)

4 重力梯度张量分量转换误差分析

4.1 误差统计

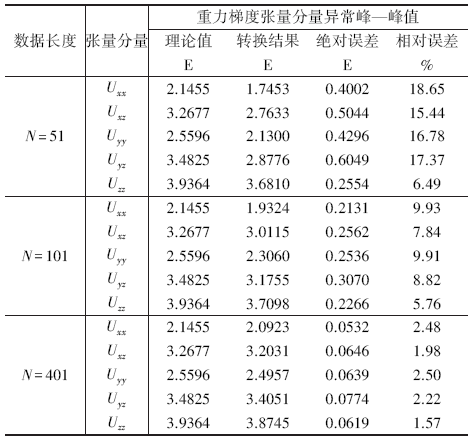
三组数据转换处理得到的各分量异常峰— 峰值与理论值误差统计见表1, 总体而言, 随着数据长度增加, 误差明显减小。当数据长度N=51时, 除U_zz分量外, 相对误差在15%~19%之间, 误差较大; 当N=101时, 相对误差小于10%; 当N=401时, 相对误差小于3%。对比各分量转换误差, U_zz转换误差最小, 最大相对误差为6.49%, 其余分量基本相当。

表1 由U_xy分量转换重力梯度张量其它分量误差统计

4.2 误差分析

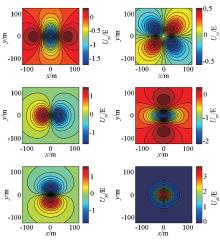
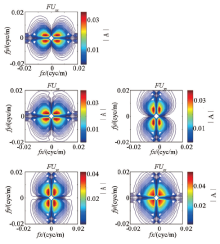
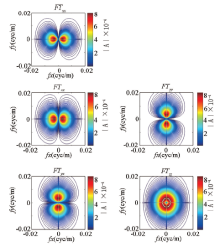
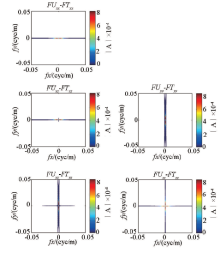
图7、图8所示分别为不同长度数据通过U_xy频谱转换得到的其他分量频谱, 与图3所示模型理论频谱相比, U_zz分量的频谱在两个频率轴上都产生了畸变, 其余分量频谱则在某一个频率轴上产生了畸变。图9、图10为相应转换得到的频谱与理论频谱之差, 对比可见, 随着数据长度的增加, 畸变频谱的能量逐步降低、影响范围逐步缩小。

	Figure Option View Download New Window
	图7 频率域转换的重力梯度张量分量振幅谱(N=51)

	Figure Option View Download New Window
	图8 频率域转换的重力梯度张量分量振幅谱(N=401)

	Figure Option View Download New Window
	图9 理论频谱与转换频谱之差(N=51)FU为理论值、FT为换算值

	Figure Option View Download New Window
	图10 理论频谱与转换频谱之差(N=401)FU为理论值、FT为换算值

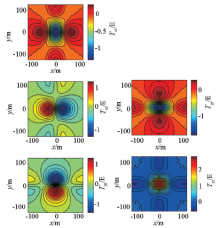
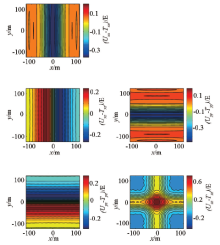
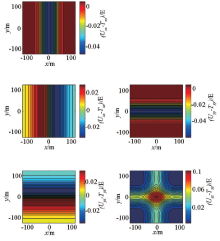
图11、图12为利用畸变频谱转换得到的空间域重力梯度张量分量异常与相应分量正演数值模拟理论值的误差, 图13、图14为模型中心剖面上的误差。由图可见:U_xx、U_yy转换误差分别沿y轴、x轴对称, U_xz、U_yz转换误差分别沿y轴、x轴对称反对称, 当数据达到一定长度时, 误差呈条带状均匀分布; U_zz转换误差相对于坐标原点呈中心对称; 从剖面图上可以看出, 转换误差曲线与原始异常曲线同相, 且呈正相关; 随着数据长度的增加, 频率分辨率提高, 转换误差逐渐减小。

	Figure Option View Download New Window
	图11 转换处理误差(N=51)U为理论值、T为换算值

	Figure Option View Download New Window
	图12 转换处理误差(N=401)U为理论值、T为换算值

	Figure Option View Download New Window
	图13 标轴上转换处理误差(N=51)U为理论值、T为转换值, 纵轴单位为E

从图7、8、9、10可以看出, 转换后频谱畸变和信号能量损失主要集中在频率轴上, 这是转换处理误差的根源, 而图11、12、13、14只是其在空间域的表现形式。转换处理后频谱畸变和空间域存在误差是由频率域转换公式(2)不完备造成的。当k_x=0、k_y=0时为奇点, 在实际应用中需要进行小量偏移处理, 由此造成对应频率轴上信号能量损失。当数据长度较短(N=51)时, 频率分辨率低、各频点权重较高, 其频谱畸变明显(图7), 对应的信号能量损失部分强度高、影响范围大(图9), 反变换后造成空间域场值抖动明显, 在极值点附近误差较大(图11、图13), 数据长度较长(N=401)时, 频率分辨率提高、各频点权重降低、影响范围缩小, 空间域场值抖动基本消失(图12、图14), 误差大幅降低。

	Figure Option View Download New Window
	图14 坐标轴上转换处理误差(N=401)U为理论值、T为转换值, 纵轴单位为E

5 结论

基于矩形棱柱体模型, 对重力梯度张量异常空间域和频率域特征进行了简要分析, 在此基础上设计了基于U_xy分量的张量分量转换处理模型实验, 并从数字信号处理的角度详细分析了转换处理空间域和频率域误差, 实验结果表明:重力梯度张量转换处理公式中的频率奇点是引起转换后频谱畸变和空间域转换误差的根源, 但在原始数据频谱带宽足够的情况下, 通过增加数据长度、提高频谱分辨率的办法, 可以大大降低转换处理误差、改善转换处理效果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	舒晴, 周坚鑫, 尹航. 航空重力梯度仪研究现状及发展趋势[J]. 物探与化探, 2007, 31(6): 485-488. [本文引用:1]
[2]	舒晴, 周坚鑫, 尹航, 等. 应用和研制中的航空重力梯度测量系统[C]//中国地球物理学会第二十七届年会论文集, 2011. [本文引用:1]
[3]	曾华霖. 重力梯度测量的现状及复兴[J]. 物探与化探, 1999, 23(1): 1-6. [本文引用:1]
[4]	张昌达. 几种新型的航空重力测量系统和航空重力梯度测量系统[J]. 物探与化探, 2005, 29(6): 471-476. [本文引用:1]
[5]	吴琼, 滕云田, 张兵, 等. 世界重力梯度仪的研究现状[J]. 物探与化探, 2013, 37(5): 761-768. [本文引用:1]
[6]	张昌达. 航空重力测量和航空重力梯度测量问题[J]. 工程地球物理学报, 2005, 2(4): 282-291. [本文引用:1]
[7]	Anstie J, Aravanis T, Johnston P. Preparation for flight testing the VK1 gravity gradiometer[C]//Airborne Gravity 2010 Abstracts from the ASEG-PESA Airborne Gravity 2010 Workshop, 2010. [本文引用:1]
[8]	曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2008. [本文引用:1]
[9]	吴宣志, 刘光海, 薛光琦, 等. 富里叶变换和位场谱分析方法及其应用[M]. 北京: 地质出版社, 1987. [本文引用:1]
[10]	Lumley J M, White J P, Barnes G, et al. A superconducting gravity gradiometer tool for Exploration[C]//Airborne Gravity 2004 Geoscience Australia Record, 2004. [本文引用:1]
[11]	程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2001. [本文引用:1]

2007

0.0

... 对于部分张量重力梯度测量^{[1,2,3,4,5,6,7]}而言,以重力位为纽带^[8],利用重力梯度张量分量之间的内在联系,通过频率域转换得到其他张量分量,从而获取更加多元的重力梯度异常信息,是简化地质解释、精化推断结果的重要手段 ...

2011

0.0

1999

0.0

2005

0.0

2013

0.0

2005

0.0

2010

0.0

2008

0.0

1987

0.0

... 1 重力梯度张量分量频率域转换公式对于平面数据,重力梯度张量各分量与重力位二维傅里叶变换关系^[9,10] ...

2004

0.0

... 1 重力梯度张量分量频率域转换公式对于平面数据,重力梯度张量各分量与重力位二维傅里叶变换关系^[9,10] ...

2001

0.0

... 3 数据长度对转换处理效果的影响在频率域^[11],信号的采样频率必须高于二倍信号最高频率(f_s#cod#x0003E ...