FD-3019型<em> γ</em>测井仪死时间修正的必要性

引用本文

马超, 管少斌, 蔡昌华. FD-3019型 γ测井仪死时间修正的必要性 [J]. 物探与化探, 2016,40(1): 100-103.
MA Chao, GUAN Shao-Bin, CAI Chang-Hua. The necessity of dead time correction of FD-3019 γ logging instrument [J]. Geophysical and Geochemical Exploration, 2016,40(1): 100-103.
Doi:10.11720/wtyht.2016.1.18 复制到剪切板

Permissions

FD-3019型 γ测井仪死时间修正的必要性

马超¹, 管少斌², 蔡昌华³

1. 核工业二四0研究所,辽宁沈阳 110032

2.核工业航测遥感中心,河北石家庄 050002

3.核工业二七0研究所,江西南昌 330200

作者简介: 马超(1983-),男,工程师,东华理工学院本科毕业,主要从事物探方面的工作。

收稿日期: 2014-09-25

基金: 中国地质调查局项目(12120113076700)

摘要

死时间是FD-3019型 γ测井仪的一个重要参数,笔者主要介绍死时间的定义、测量、计算和修正的方法,通过对多个钻孔测井数据死时间修正前后进行对比,并分别计算出钻孔内铀矿段含量,求出相对误差,进而说明死时间修正的必要性。

关键词: 测井仪; 死时间; 修正; 误差

中图分类号:P632 文献标志码:A 文章编号:1000-8918(2016)01-0100-04 doi: 10.11720/wtyht.2016.1.18

The necessity of dead time correction of FD-3019 γ logging instrument

MA Chao¹, GUAN Shao-Bin², CAI Chang-Hua³

1.No.240 Research Institute,CnnC,Shenyang 110032,China

2.Airborne Survey and Remote Sensing Center,CnnC,Shijiazhuang 050002,China

3.No.270 Research Institute,CnnC,Nanchang 330200,China

Abstract

Dead time is a very important parameter of FD-3019 γ logging instrument.This paper described the definition of dead time,introduced measurement,calculation and correction methods of dead time,explained the necessity of dead time correction by comparing revised data and calculated the errors of uranium content in the drill holes.

Keyword: γlogging instrument; dead time; correction; errors

Show Figures

在放射性测井中, 通常使用上海申核电子仪器有限公司生产的FD-3019型γ 测井仪来确定铀矿层的厚度、品位以及储量等。按照γ 测井规范要求, 仪器每年都需经过核工业放射性勘查计量站的检定, 在检定证书中, 有一个不能忽视的重要参数— — 死时间τ 。

1 死时间定义

由于FD-3019型γ 测井仪采用的是脉冲式γ 总量测井的方法, 其测量的能量范围为0.4~3 MeV。对于FD-3019型γ 测井仪来说, 死时间可以被定义为能区分两个脉冲之间的最小时间间隔, 其大小由探测器件的分辨率和配套的电子学电路共同决定, 一般取决于两者之中最大的一个。死时间也可以理解为γ 测井仪对辐射的响应恢复时间。

死时间又分“ 扩展型” (可延续型或累积型)和“ 非扩展型” (可延续型)两种。它们的区别在于对死时间内所到达脉冲的响应不同, 扩展型是在死时间内, 由最后脉冲到达时刻起再把死时间延长; 非扩展型是对在死时间内到达的脉冲完全没有响应。而FD-3019型γ 测井仪的死时间是非扩展型死时间, 因为在死时间内到达的脉冲没有引起计数, 但也不会进一步引起死时间的增加。

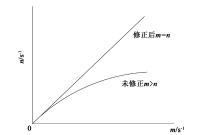
辐射具有随机性, 在死时间内, 存在着一定的辐射几率, 这个几率与辐射强度成正比, 由于γ 测井仪的死时间是非扩展型, 所以探头在死时间内将不能区分下一个脉冲的到来, 造成两个或多个脉冲被堆叠到了一起。计数率越高, 堆叠在一起的概率就越大, 对总的脉冲计数影响也就越大(图1)。

	Figure Option View Download New Window
	图1 计数率在死时间修正前后的关系m为真实计数率, n为实测计数率

2 死时间测量

按照γ 测井仪检定规程要求, 应选择模型体源或固体镭标准源来进行测量。前者至少应选择两个含量合适的铀模型体源, 后者至少应选择两个合适的空气比释动能率值, 且要求两个模型体源的铀含量或两个空气比释动能率值应相差5~10倍。

为了评价不同铀含量或不同空气比释动能率值的死时间变化, 可采用几对模型体源或几对空气比释动能率值。要求每个点或每个模型体源的读数应不少于10次。

核工业放射性勘查计量站采用模型体源的测量方式, 优点是放射源强度稳定, 测井仪处于密闭环境, 不受其他条件影响。

放射性强度公式为

$\begin{matrix} X = \frac{A}{r^{2}}, \end{matrix}$ (1)

其中:X为放射性强度, 单位Bq; A为镭标准源常数, 单位(nGy· m²)/h; r为测量点到放射源的距离, 单位m。

本次实验采用的是固体镭源测量方式。先给定若干个强度值, 按照放射性强度公式(1), 计算出各给定强度所对应的距离。把γ 测井仪固定在检定架上, 将固体镭源中心与γ 测井仪测量点标线处于同一水平高度, 且距离地面高度约2 m, 然后用钢卷尺准确测量距离, 并按照各距离逐点测量。测量方式采用连续测量, 每个测点的读数都在500次以上, 取平均值参与计算, 结果见表1。

表1 各强度下的测量距离和计数率

3 死时间计算

按上述方法测量, γ 测井仪的死时间τ 应按公式(2)计算

$\begin{matrix} τ = \frac{N_{L} - R \cdot H_{H}}{N_{L} \cdot N_{H} \cdot (1 - R)}, \end{matrix}$ (2)

其中:τ 为γ 测井仪的死时间, 单位s; N_L为在低含量模型体源(或固体镭标准源低空气比释动能率值)上的测量结果, 单位为s^-1; R为低模型体源的含量(或固体镭标准源低空气比释动能率值)与高模型体源的含量(或固体镭标准源高空气比释动能率值)的比值; N_H为在高含量模型体源(或固体镭标准源高空气比释动能率值)上的测量结果, 单位s^-¹。

按照两个空气比释动能率值应相差5~10倍的要求, 选出13组数据, 计算结果如表2所示。

表2 实验测得的计数率及死时间

计算出的结果平均值为3.99 μ s, 和放射性勘查计量站测算出的3.90 μ s相对误差为2.3%, 但个别测点的误差较大, 超过了5%的要求, 其原因是由于实验所使用的固体5号镭源活度小, 在测得较大计数率时, γ 测井仪和镭源距离过近(最小距离不足半米), 稍有误差, 就会产生较大影响; 另外由于在户外进行测量, 微风等气候因素也容易造成镭源摆动, 影响结果的准确性。

4 死时间修正

γ 测井仪的死时间修正应按公式

$\begin{matrix} N_{τ} = \frac{N_{0}}{1 - τ \cdot N_{0}} \end{matrix}$ (3)

计算, 其中:N_τ为经过死时间修正后的测量结果, 单位s^-1; N₀为未经过修正的原始测量值, 单位s^-1。

依据式(3), 对K548孔的伽玛测井原始曲线进行死时间修正, 绘制对比曲线(图2)。从图中可以看出, 计数率越高, 误差越大。

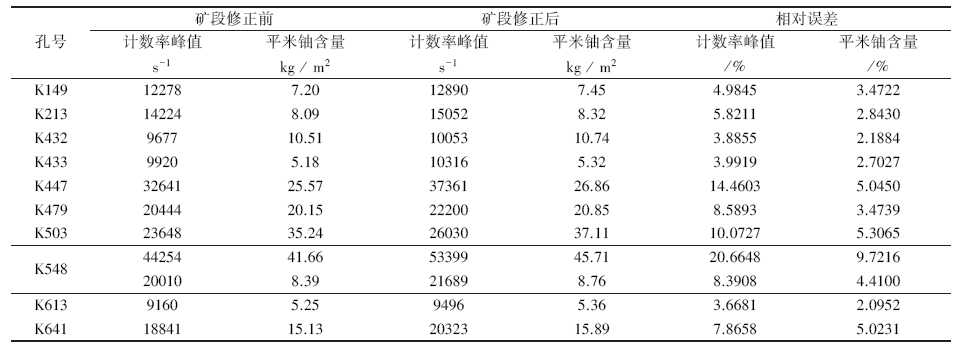
	Figure Option View Download New Window
	图2 K548孔伽马测井原始曲线死时间校正前后对比

选取了近年来几个品位较高钻孔(砂岩型铀矿)的矿段, 按式(3)对死时间进行修正, 并计算出修正前后伽玛计数率的相对误差。再应用核工业地质局内部研发的测井资料处理解释系统中γ 测井解释模块, 按式(4)计算出该计数率峰值所处矿段的平米铀含量。由于砂岩型铀矿的工业指标是以平米铀含量作为参考, 故文中以平米铀含量进行对比, 并计算出修正前后的平米铀含量相对误差(表3)。计算公式为

$\begin{matrix} Y = H \cdot C \cdot ρ, \end{matrix}$ (4)

其中:Y为平米铀含量, 单位kg/m²; H为由边界品位确定的矿层厚度, m; C为通过五点式反褶积分层解释法求得的品位, 单位eU0.01%; ρ 为岩石密度, 单位g/cm³。

表3 死时间修正前后误差统计

从表3中可以看出, 当计数率达到50 000时, 修正前后误差超过20%, 单层矿段的平米铀含量误差近10%, 也就是说矿层的品位越高, 影响就越大。

5 结论

综上所述, γ 测井数据的死时间修正非常重要, 尤其是在高品位铀矿储量的计算上, 品位越高, 影响越大, 如果用在整个矿床的储量统计上, 影响是相当大的。随着找矿技术和方法的不断进步, 或将发现更大规模储量的矿床, 因此在γ 测井数据的处理解释上, 必须进行死时间修正。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	EJ/J 1-2007γ测井仪检定规程. [本文引用:1]
[2]	EJ/T 611-2005γ测井规范. [本文引用:1]
[3]	陆士立, 焦仓文, 赵丹. γ能谱测井仪的死时间修正方法[C]//全国铀矿大基地建设学术研讨会论文集(下), 2012. [本文引用:1]
[4]	刘建忠, 靳根, 马立平, 等. FP-180系统死时间测量[J]. 核标准计量与质量, 2006, (3): 25-30. [本文引用:1]
[5]	伍怀龙, 杨晓波, 唐元明. 死时间和源不均匀性对γ测量准确性的影响[J]. 中国核科技报告, 2003, (4): 356-364. [本文引用:1]
[6]	乐仁昌, 贾文懿, 吴允平, 等. 一种新的死时间内事件丢失的补偿方法及其实现[J]. 核电子学与探测技术, 2002, 22(2): 114-116. [本文引用:1]
[7]	郑春, 宋凌莉, 艾自辉, 等. 计数率测量仪死时间的确定方法[J]. 原子能科学技术, 2011, 45(11): 1369-1371. [本文引用:1]
[8]	胡欣宇, 韩克宁. 油气田放射性测井技术在铀矿应用中的若干问题及解决办法[J]. 科技信息, 2010, (6): 342-343. [本文引用:1]
[9]	汤彬. γ测井分层解释法[M]. 北京: 原子能出版社, 1993. [本文引用:1]
[10]	李丽华, 徐鹍, 石宗仁, 等. 高纯锗探测器使用中高计数率的影响[J]. 中国原子能科学研究院年报, 2010: 174. [本文引用:1]
[11]	伍怀龙, 章剑华, 储诚胜, 等. γ探测死时间与计数修正因子的关系[J]. 原子能科学技术, 2015, 49(1): 162-165. [本文引用:1]
[12]	Yi C Y. Nuclear instruments and methods in physics research[M]. Elsevier Science, 2005. [本文引用:1]
[13]	吴静. 自然伽马测井解释中死时间修正的必要性[J]. 西部探矿工程, 2012, (3): 103-105. [本文引用:1]
[14]	刘国才. GM计数管死时间及其对辐射测量的影响[J]. 核电子学与探测技术, 1990, 10(2): 92-96. [本文引用:1]
[15]	王强, 方开洪, 周钰珊, 等. HPGe-γ谱仪系统的死时间校正[J]. 原子能科学技术, 2013, 33(9): 1119-1122. [本文引用:1]