磁化率对大地电磁响应的影响及其提取方法

引用本文

王珺璐, 王萌, 李荡, 李建华, 林品荣. 磁化率对大地电磁响应的影响及其提取方法[J]. 物探与化探, 2017,39(6): 1292-1298.
WANG Jun-Lu, WANG Meng, LI Dang, LI Jian-Hua, LIN Pin-Rong. The influence of magnetic susceptibility on MT response and its extraction method[J]. Geophysical and Geochemical Exploration, 2017,39(6): 1292-1298. 复制到剪切板

Doi:10.11720/wtyht.2015.6.32
Permissions

《物探与化探》编辑部

磁化率对大地电磁响应的影响及其提取方法

王珺璐¹, 王萌², 李荡¹, 李建华¹, 林品荣¹

1. 中国地质科学院地球物理地球化学勘查研究所,河北廊坊 065000

2. 中国国土资源航空物探遥感中心,北京 100083

作者简介:王珺璐(1988-),男,硕士,助理工程师,主要专业方向为电磁法数值模拟与方法应用研究。E-mail:wangjunlu2007@126.com

收稿日期: 2015-10-12

基金: 国家重大科学仪器设备开发专项(2011YQ050060); 国家高技术研究发展计划(2014AA06A610); 中国地质科学院地球物理地球化学勘查研究所基本科研业务费专项资金(AS2014D01,AS2013R02)

摘要

在电磁探测理论中,电导率和磁导率是两个重要的岩石物性参数。在磁性较强的地区进行大地电磁探测工作时,电磁场信号必然受到介质磁性的影响。将磁化率参数引入到二维大地电磁正演理论中,实现了含磁化率的大地电磁有限单元法数值模拟。建立棱柱体模型计算并分析了磁化率参数对大地电磁的电场、磁场、视电阻率及相位等参数的影响。数值模拟结果表明:高磁性介质导致电场升高,磁场降低,视电阻率增大,相位复杂变化,且随着磁性物质的增多或磁化率的增大,这种影响逐渐变大。引入电导率、磁化率光滑约束与磁化率对数约束,采用改进的特别快速模拟退火法实现了电阻率、磁化率参数一维同时反演。对K型、H型中间层高磁地电模型进行反演试算,反演结果良好。该研究为在高磁性地区开展大地电磁工作提供了基础,对实现“第二找矿空间”内的矿产勘探,具有一定的意义。

关键词: 磁化率; 电阻率; 大地电磁; 有限单元法; 模拟退火法

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)06-1292-07

The influence of magnetic susceptibility on MT response and its extraction method

WANG Jun-Lu¹, WANG Meng², LI Dang¹, LI Jian-Hua¹, LIN Pin-Rong¹

1.Institute of Geophysical and Geochemical Exploration,CAGS,Langfang 065000,China

2.China Aero Geophysical Survey and Remote Sensing Center for Land and Resources,Beijing 100083,China

Abstract

In electromagnetic theory,conductivity and permeability are two important petrophysical parameters.The electromagnetic signal will inevitably be affected by the magnetic properties of the media in MT detection where magnetism is strong.The authors made the numerical simulation of the electromagnetic finite element method with magnetic susceptibility by introducing the magnetic susceptibility parameter into the two-dimensional MT forward theory.Prism model was established for calculation and analysis of the influence of the magnetic susceptibility parameters on the electric field,magnetic field,MT apparent resistivity and phase parameters.The numerical simulation results show that the high magnetic medium results in increasing the electric field,reducing the magnetic field,increasing the apparent resistivity,and complex changes of phase and,with the increase of the magnetic substance or the increase of the magnetization rate,the effect gradually becomes larger.The inversion results of geoelectric model with high magnetic middle layer are good.The results obtained by the authors provide a theoretical basis for the MT work in the high magnetic area and also have a certain significance for conducting the mineral prospecting in "the second space".

Keyword: Magnetic susceptibility; resistivity; MT; finite element method; simulated annealing method

Show Figures

天然场电磁法具有不受高阻层屏蔽、勘探深度大、费用低、施工方便等特点, 并广泛应用于基础地质调查、能源矿产勘查、水文工程环境等地质勘查工作^{[1, 2, 3, 4, 5]}。在电磁探测理论中, 电导率和磁导率是两种重要的岩石物性参数^[6]。但在传统大地电磁法(MT)的模拟研究时, 通常不考虑介质的相对磁导率, 将介质磁导率用真空磁导率进行替代。实际情况下, 无论是磁性较强的岩浆岩、变质岩, 还是含铁磁性矿物的矿石, 其磁导率明显大于真空磁导率。在磁性较强的地区进行电磁探测工作时, 若不考虑介质的磁性, 其电阻率等测量结果必然存在误差。另外, 由于大地电磁能够提供垂向的物性变化信息, 若能在有利的条件下提取出磁性参数, 则具有一定的应用价值。

为了研究磁化率对大地电磁响应的影响, 许多学者先后开展了一系列的工作。Fraser^[7]、Thoms^[8]等人分别研究了航空电磁信号中的磁化率响应; 李学民^[9]认为磁化率主要影响大地电磁磁场的同相分量, 对磁场的异相分量及电场影响较弱; 刘应冬^[10]研究认为高阻地质体中较低阻体对磁化率反应更加灵敏。在磁化率参数提取方面, Zhang^[11]在假设电阻率分布已知的情况下, 利用频率域的电磁数据进行磁化率一维反演。当缺少先验条件时, 就要进行电阻率参数和磁化率参数同时反演。Beard^[12]尝试利用航空电磁信号同时反演电阻率参数和磁化率参数; Zhang^[13]实现了利用单一数据同时反演一维电阻率和磁化率的算法; Fqarhuasro^[14]在反演中引入磁化率对数约束, 对线圈电磁数据进行了电阻率和磁化率一维反演。李学民^[15]采用带限约束的迭代方法进行了电阻率和磁化率反演研究, 并应用于火山岩分布区地质构造勘查。目前, 在处理非线性反演问题时, 一般都是采用线性化的办法来将问题进行简化。

笔者在前人的基础上, 将磁化率参数引入到二维大地电磁正演理论中, 实现了含磁化率的MT有限单元法数值模拟, 建立棱柱体模型计算并分析了磁化率参数对MT电场、磁场、视电阻率及相位等参数的影响。引入电导率、磁化率光滑约束与磁化率对数约束, 采用改进的特别快速模拟退火法实现了电阻率、磁化率一维同时反演。该研究为在高磁性地区开展大地电磁工作提供了基础, 对实现“ 第二找矿空间” (500 ~2 000 m)内的矿产勘探, 具有一定的意义^[16]。

1 岩矿石的磁性

磁导率是电磁法中的重要物性参数, 表征物质在磁化作用下集中磁力线的性质。磁感应强度B与磁场强度H关系^[17]为B=μ H, 式中, μ 为介质磁导率, 规定真空中的磁导率为μ ₀=4π × 10^-⁷H/m, 则有

$\begin{matrix} μ = μ_{0} μ_{r} = μ_{0} (1 + κ), \end{matrix}$

式中, μ _r为介质的相对磁导率, 无量纲; κ 为介质磁化率, 单位为SI。

对三大类岩石来说, 岩石磁导率的大小与其中所含铁磁性矿物的多少有关, 一般沉积岩的磁性较弱, 当不含铁质时可视为无磁性; 火成岩的磁性较强, 从花岗岩到辉长岩再到玄武岩, 磁性逐渐增强; 变质岩磁性介于两者之间, 与原岩的磁性及生成条件有关, 特殊者也具有较高的磁性。朴化荣^[18]指出岩矿石的相对磁导率与铁磁性矿体积含量有关, 认为沉积岩的μ _r一般不超过1.004, 岩浆岩和变质岩的μ _r一般不超过1.04, 但是当岩石中磁铁矿含量增加时, μ _r可达到1.4。例如, 玄武岩中磁铁矿体积百分含量达到4%时, μ _r就可接近1.2。当岩石中磁铁矿含量增加到20%时, μ _r可达到1.57。

含铁磁性矿物岩石的μ _r大于真空磁导率。其中, 黄铁矿μ _r一般为1.0015, 赤铁矿μ _r一般为 1.05, 钛铁矿μ _r一般为1.55, 磁黄铁矿μ _r一般为 2.55, 磁铁矿μ _r可以达到5^[19]。

因此, 无论是磁性较强的岩浆岩、变质岩, 还是含铁磁性矿物的矿石, 其磁导率明显大于真空磁导率。在磁性较强的地区进行电磁探测工作时, 若不考虑介质的磁性, 其电阻率等测量结果必然存在误差。

2 磁化率对大地电磁响应影响规律

采用有限单元法进行磁性介质的大地电磁二维数值模拟, 编程序对大地电磁方法的无磁性、磁性强度变化的高、低阻棱柱体模型进行了计算, 分析了大地电磁的电磁场分量、视电阻率和相位的响应特征; 由此, 研究大地电磁法测得参数受磁化率的影响程度。

2.1 二维有限元数值模拟方法

假定地下构造是二维的, 走向取为z轴, x轴与z轴垂直, 保持水平, y轴垂直向上。根据麦克斯韦方程, 可推导得到z方向电磁场E_z和H_z满足的偏微分方程^[20]:

$\begin{matrix} \nabla \cdot (τ \nabla u) + λu = 0 。 \end{matrix}$

对于TE模式:u=E_z, τ =1/iω μ , λ =σ -iω ε ; 对于TM模式:u=H_z, τ =1/(1-iω ε ), λ =iω μ 。式中, ∇为二维哈密顿算子, ω 为角频率, ε 为介电常数, σ 为电导率; 当介质磁导率不为真空磁导率时, 采用μ =μ ₀(1+κ )进行计算。等价的变分问题为

$\begin{matrix} \begin{matrix} F [u] = & \int_{Ω} [\frac{1}{2} τ {(\nabla u)}^{2} - \frac{1}{2} λ u^{2}] dΩ + \\ \int_{CD} \frac{1}{2} τk u^{2} dΓ \\ u |_{AB} = & 1 \\ δF [u] = & 0 。 \end{matrix} \end{matrix}$

求解变分问题, 对区域Ω 采用矩形网格单元进行网格剖分, 剖分时采用非等间距剖分, 网格间距由内向外, 由浅向深逐渐加大。将对区域Ω 的积分分解为对各单元e的积分之和, 单元内部采用双线性插值方法进行插值, 采用定带宽存储方式进行总体系数矩阵的组装^[21]。采用LDLT方法进行方程组的求解, 获得模型每一个节点的u, TM模式对应H_z, TE模式对应E_z。取近地表的4个等距节点的u来计算导数u/y, TM模式对应E_x, TE模式对应H_x, 进而求得视电阻率与相位等参数。

	Figure Option View Download New Window
	图1 棱柱体模型示意

2.2 磁化率对大地电磁响应影响规律

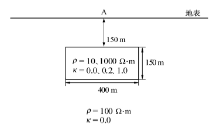
建立棱柱体模型(图1), 计算含磁性大地电磁响应。棱柱体尺寸400 m× 150 m, 顶界面埋深150 m。背景电阻率为100 Ω · m, 棱柱体电阻率可变, 低阻为10 Ω · m, 高阻为1 000 Ω · m。背景无磁性, 棱柱体磁化率可变, 磁化率取0.0、0.2、1.0分别模拟无磁性、火成岩侵入构造及磁铁矿的磁性特征。频率范围为10^-3~10⁴ Hz。

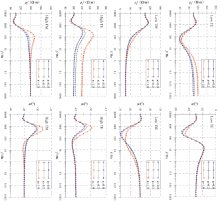
	Figure Option View Download New Window
	图2 磁化率对视电阻率与相位的影响

抽取位于棱柱体正上方点A的视电阻率(ρ _s)和相位(φ )曲线(图2), 分析磁化率参数对视电阻率及相位的影响规律。可以看出:①当地下介质的磁化率大于真空中磁化率时, 磁化率对MT视电阻率及相位会产生明显的影响, 且随着磁性物质的增多或磁化率的增大, 这种影响逐渐变大; ②无论是TE模式还是TM模式, 低阻异常体还是高阻异常体, 磁化率的存在导致视电阻率升高, 相位变化相对更加复杂; ③TE模式要比TM模式变化更明显, 磁化率对TE模式的影响体现在全频段, 对TM模式的影响体现在反应棱柱体深度的相应频段。

	Figure Option View Download New Window
	图3 低阻体电场、磁场、视电阻率比值和相位差值曲线

按文献[21]中的方法, 对磁化率为1.0的模型与无磁性模型进行归一, 取考虑磁性和未考虑磁性前后的电场比值 $\begin{matrix} B_{E_{x}} \end{matrix}$ 、磁场比值 $\begin{matrix} B_{H_{y}} \end{matrix}$ 、视电阻率比值 $\begin{matrix} B_{ρ_{s}} \end{matrix}$ 和相位差值D, 非异常频段B=1, D=0。对于低阻体(图3), TM模式下电场最大增加约14%, 磁场衰减不明显, 视电阻率最大增加约30%, 相位在 300 Hz 附近增大约8° , 在10 Hz附近减小约4° ; TE模式下电场最大增加约8%, 磁场衰减较复杂, 最大约10%, 视电阻率最大增加约25%, 相位在400 Hz附近增大约7° , 在70 Hz附近减小约2° 。对于高阻体(图4), TM模式下电场最大增加约9%, 磁场衰减不明显, 视电阻率最大增加约20%, 相位在500 Hz附近增大约6° , 在30 Hz附近减小约3° ; TE模式下电场最大增加约6%, 磁场衰减最大约9%, 视电阻率最大增加约25%, 相位在500 Hz附近增大约8, 在 10 Hz 附近减小约1° 。综合分析可以看出:无论是TE模式还是TM模式, 低阻异常体还是高阻异常体, 磁化率导致电场升高, 磁场降低。

	Figure Option View Download New Window
	图4 高阻体电场、磁场、视电阻率比值和相位差值曲线

因此, 磁化率对大地电磁响应产生显著影响, 导致电场升高, 磁场降低, 视电阻率增大, 相位复杂变化, 随着磁性物质的增多或磁化率的增大, 这种影响逐渐变大, 且TE模式较TM模式对磁化率参数反映更加灵敏。在高磁性地区进行电磁探测时, 必须考虑磁化率对大地电磁的影响。

3 磁化率参数的提取

目前, 从电磁信号中提取电性参数时一般采用反演的方法^[22]。在磁化率参数提取方面, 若已知地下介质电阻率分布的情况下, 进行单一磁化率参数的反演, 可以较好的获得磁化率分布结果。但是实际情况中往往缺少电阻率先验信息, 这时必须进行电阻率参数和磁化率参数同时反演。由于波数k= $\begin{matrix} \sqrt{- iωμσ} \end{matrix}$ , 式中电导率σ 与磁导率μ 具有相乘的关系, 因而同时反演问题是一个非线性问题^[15]。笔者尝试利用改进的模拟退火法(MVFSA)进行反演。

3.1 改进的模拟退火算法

模拟退火算法(SA)及相应的改进算法是解决非线性反演问题的重要方法, 该方法不用求目标函数的偏导数, 不用解大型矩阵方程组, 即能找到一个全局最优解, 而且易于加入约束条件^{[23, 24, 25, 26]}。笔者采用陈华根^[27]提出的改进的特别快速模拟退火(MVFSA)算法开展电阻率与磁化率参数的同时反演。MVFSA算法通过全局扰动搜索最优解空间, 在最优解空间内进行局部扰动搜索最优解。另外, 在退火过程中进行回火升温, 设立跳出局部极值机制, 使得反演结果更加可靠。

搜索最优解区间时, 进行全局扰动, 扰动方式为

$\begin{matrix} M_{i}^{'} = B_{i} + u (B_{i} - A_{i}), \end{matrix}$

式中:m_i与 $\begin{matrix} m_{i}^{'} \end{matrix}$ 分别为模型中第i个变量扰动前与扰动后的值, u为(0, 1)间的随机数, (A_i, B_i)为m_i的上下限。

退火计划为

$\begin{matrix} T = T_{0} \cdot \exp [- α \cdot {(j - 1)}^{\frac{1}{2}}], \end{matrix}$

式中:T₀为初始仿真温度, α 为衰减律, j为迭代次数。

回火升温, 进行局部扰动时, 扰动方式及退火计划修改为

$\begin{matrix} \begin{matrix} M_{i}^{'} = m_{i} + (u - 0.5) (B_{i} - A_{i}) / L, \\ T = T_{0} \cdot \exp [- α \cdot {(j - k / β)}^{\frac{1}{2}}], \end{matrix} \end{matrix}$

式中:L为空间搜索范围的限制因子, k为搜索最优解区间的迭代次数, β 为温度升幅因子。

接收概率的计算公式为

$\begin{matrix} P = [1 - {(1 - q) ΔE / T]}^{1 / (1 - q)}, \end{matrix}$

式中:Δ E为扰动前后的能量差, q为接近于1的实数。

3.2 目标函数

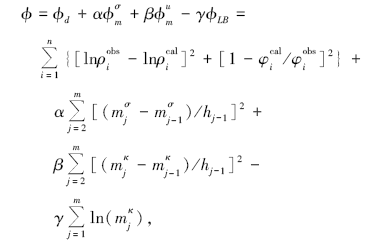
朴化荣在文献[13]中详细推导了大地电磁一维正演公式, 将磁化率引入正演公式, 实现了含磁性大地电磁一维正演。进行电阻率与磁化率同时反演时, 采用最小构造思想^{[28, 29]}, 引入电导率与磁化率光滑约束; 同时为保证磁化率为正, 引入磁化率对数约束^{[14, 30]}。最终目标函数由拟合差项ϕ _d, 电导率、磁化率的粗糙度项 $\begin{matrix} ϕ_{m}^{σ} \end{matrix}$ 与 $\begin{matrix} ϕ_{m}^{κ} \end{matrix}$ , 磁化率对数约束项ϕ _LB组成:

式中:n为频点数, m为模型层数, $\begin{matrix} ρ_{i}^{cal} \end{matrix}$ 与 $\begin{matrix} φ_{i}^{cal} \end{matrix}$ 分别为第i个频点正演视电阻率与相位, $\begin{matrix} ρ_{i}^{obs} \end{matrix}$ 与 $\begin{matrix} φ_{i}^{obs} \end{matrix}$ 分别为第i个频点观测视电阻率与相位, $\begin{matrix} m_{j}^{σ} \end{matrix}$ 与 $\begin{matrix} m_{j}^{κ} \end{matrix}$ 分别为反演模型第j层电导率与磁化率, α 与β 为拉格朗日乘子, γ 为约束项系数。

对反演中拉格朗日乘子α 与β 设置为固定参数。由于大地电磁对电阻率较磁化率反应更加灵敏, 所以首先要保证能够获得可靠的电阻率反演结果, 在理想条件下提供合适的磁化率反演结果; 因此α 取值应稍大于β 。对数约束系数γ 设置为浮动参数, 可以在反演开始给定初值及迭代步长, 随迭代次数增加γ 逐渐变小, 当γ 趋近于0时, 获得电阻率与磁化率参数的最优解。

目标函数中的粗糙度项包含层厚, 为减少模型参数, 层厚采用预先设定的方式给定。由于大地电磁的分辨率随深度加大呈指数降低, 为不引入多余构造, 分层时选用对数等间隔的方式进行划分。

3.3 理论模型反演

建立模型一为低阻高磁三层理论模型, 电阻率参数ρ ₁=50 Ω · m, ρ ₂=10 Ω · m, ρ ₃=50 Ω · m; 磁化率参数κ ₁=0 SI, κ ₂=0.5 SI, κ ₃=0 SI; 层厚h₁=300 m, h₂=500 m。

反演时频率范围为0.017~320 Hz, 设定模型空间为理论模型参数的± 50%, 模型层数为15, 初始仿真温度T₀=500 K, 衰减率α =0.98, q=0.25; 温度升幅因子β =2, 空间搜索范围的限制因子L=10; 在每一温度下对模型参数进行10次扰动。

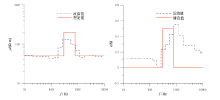
从模型反演结果(图5)可以看出:电阻率反演结果基本与实际模型吻合良好, 磁化率反演结果也基本能反映实际模型参数; 但是高值区反演结果偏深, 厚度偏大, 这是因为随深度变大, 大地电磁分辨率降低。

	Figure Option View Download New Window
	图5 低阻模型电阻率、磁化率反演结果

建立模型二为高阻高磁三层理论模型, 磁化率参数和层厚参数不变, 电阻率参数ρ ₁=50 Ω · m, ρ ₂=200 Ω · m, ρ ₃=50 Ω · m。高阻模型的反演结果(图6)中, 中间高阻高磁层也有一定的体现。

	Figure Option View Download New Window
	图6 高阻模型电阻率、磁化率反演结果

4 结论

无论是磁性较强的岩浆岩、变质岩, 还是含铁磁性矿物的矿石, 其磁导率明显大于真空磁导率。地下高磁化率介质会导致大地电磁电场升高, 磁场降低, 视电阻率增大, 相位复杂变化, 随着磁性物质的增多或磁化率的增大这种影响逐渐变大, 且TE模式较TM模式对磁化率参数反映更加灵敏。因此, 在磁性较强的地区进行电磁探测工作时, 为保证测量精度必须考虑磁化率对大地电磁的影响。

引入电导率、磁化率光滑约束与磁化率对数约束, 采用改进的特别快速模拟退火法实现了电阻率、磁化率一维同时反演, 模型反演结果能较好地反应实际地电模型。该研究为在高磁性地区开展大地电磁工作提供了基础, 对实现“ 第二找矿空间” 内的矿产勘探, 具有一定的意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	魏文博. 我国大地电磁测深新进展及瞻望[J]. 地球物理学进展, 2002, 17(2): 245-254. [本文引用:1]
[2]	李爱勇, 柳建新, 朱春生, 等. 大地电磁测深在桂中坳陷油气勘探中的应用[J]. 物探与化探, 2012, 36(1): 8-12. [本文引用:1]
[3]	姚大为, 朱威, 王大勇, 等. 音频大地电磁法在武山外围深部勘查中的应用[J]. 物探与化探, 2015, 39(1): 100-103. [本文引用:1]
[4]	杨学明, 苏永军, 杜东, 等. 音频大地电磁法在海水入侵动态监测中的应用[J]. 物探与化探, 2013, 37(2): 301-305. [本文引用:1]
[5]	武毅, 封绍武, 王亚清. 应用大地电磁法TE、TM模式勘查构造裂隙水[J]. 物探与化探, 2011, 35(3): 329-332. [本文引用:1]
[6]	米萨克N 纳比吉安. 勘查地球物理电磁法[M]. 赵经祥, 译. 北京: 地质出版社, 1992. [本文引用:1]
[7]	Fraser D C. Magnetite ore tonnage estimates from an aerial electromagnetic survey[J]. Geoexploration, 1973(11): 97-105. [本文引用:1]
[8]	Thomas L. Electromagnetic sounding with susceptibility among the model parameters[J]. Geophysics, 1997, 42(1): 92-96. [本文引用:1]
[9]	李学民, 曹俊兴. 磁化率对大地电磁响应的影响研究[J]. 地球物理学报, 2005, 48(4): 947-950. [本文引用:1]
[10]	刘应冬, 谭捍东, 宋文杰. 磁化率参数对大地电磁响应的影响研究[J]. 地球物理学进展, 2014, 29(5): 2040-2046. [本文引用:1]
[11]	Zhang Z Y, Oldenburg D W. Recovering magnetic susceptibility from electromagnetic date over a one-dimensional earth[J]. Gocphys. J. Int. 1997(130): 422-434. [本文引用:1]
[12]	Beard L P, Nyquist J E. Simultaneous inversion of airborne electromagnetic date for resistivity and magnetic permeability[J]. Geophysics, 1998, 63(5), 1556-1564. [本文引用:1]
[13]	Zhang Z Y, Oldenburg D W. Simultaneous reconstruction of 1-D susceptibility and conductivity from electromagnetic date[J]. Geophysics, 1999(64): 33-47. [本文引用:1]
[14]	Farquharson C G, Oldenburg D W. Simultaneous one-dimensional inversion of electromagnetic loop-loop data for both magnetic susceptibility and electrical conductivity[J]. Geophysics, 2003, 68(6): 1857-1869. [本文引用:2]
[15]	曹俊兴, 李学民, 贺振华. 考虑磁参数MT反演[C]//第六届中国国际地球电磁学术讨论会, 2003. [本文引用:2]
[16]	滕吉文. 强化开展地壳内部第二深度空间金属矿产资源地球物理找矿、勘探和开发[J]. 地质通报, 2006, 25(7): 767-771. [本文引用:1]
[17]	管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005. [本文引用:1]
[18]	朴化荣. 电磁探测法原理[M]. 北京: 地质出版社, 1990. [本文引用:1]
[19]	李貅, 冯兵. 应用地球物理基础教程(上)[M]. 西安: 陕西人民教育出版社, 2003. [本文引用:1]
[20]	徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994. [本文引用:1]
[21]	王珺璐, 刘明文, 李荡, 等. 基于Cole-Cole复电阻率模型的线源可控源有限元数值模拟[J]. 物探化探计算技术, 2015, 37(1): 32-39. [本文引用:1]
[22]	冯兵, 王珺璐, 王玉, 等. 利用CSAMT电磁场响应提取激电效应的方法初探[J]. 地球物理学进展, 2013, 28(4): 2116-2122. [本文引用:1]
[23]	于鹏, 王家林, 吴健生, 等. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 2007, 50(2): 529-538. [本文引用:1]
[24]	师学明, 王家映. 地球物理资料非线性反演方法讲座(三) 模拟退火法[J]. 工程地球物理学报, 2007, 4(3): 165-174. [本文引用:1]
[25]	师学明, 王家映. 一维层状介质大地电磁模拟退火反演法[J]. 工程地球物理学报, 1998, 23(5): 542-545. [本文引用:1]
[26]	杨辉, 王家林, 吴健生, 等. 大地电磁与地震资料仿真退火约束联合反演[J]. 地球物理学报, 2002, 45(5): 723-734. [本文引用:1]
[27]	陈华根, 吴健生, 王家林. 改进的重力模拟退火反演研究[J]. 吉林大学学报: 地球科学版, 2002, 32(3): 294-298、303. [本文引用:1]
[28]	李帝铨, 王光杰, 底青云, 等. 基于遗传算法的CSAMT最小构造反演[J]. 地球物理学报, 2008, 51(4): 1234-1245. [本文引用:1]
[29]	汤井田, 张林成, 肖晓. 基于频点CSAMT一维最小构造反演[J]. 物探化探计算技术, 2011, 33(6): 577-581, 571. [本文引用:1]
[30]	Li Y G, Oldenburg D W. Fast inversion of large-scale magnetic data using wavelet transforms[J]. Geophysics, 2003, 152(2): 251-265. [本文引用:1]

2002

0.0

魏文博. 我国大地电磁测深新进展及瞻望[J]. 地球物理学进展, 2002, 17(2): 245-254.

A brief review of China's MT is given here for 60s, 70s and 80s of last century. Since 90s China's MT had a great progress and a detailed review is introduced. The prospect of MT in 21th century is also discussed.

China University of Geosciences, Beijing 100083, China

简要回顾了上世纪60-80年代,我国大地电磁测深工作的起步和发展,较全面地介绍了90年代以来的新进展,并瞻望了新世纪的发展方向.

... 天然场电磁法具有不受高阻层屏蔽、勘探深度大、费用低、施工方便等特点,并广泛应用于基础地质调查、能源矿产勘查、水文工程环境等地质勘查工作^[1,2,3,4,5] ...

2012

0.0

李爱勇, 柳建新, 朱春生, 等. 大地电磁测深在桂中坳陷油气勘探中的应用[J]. 物探与化探, 2012, 36(1): 8-12.

According to the exploration results of two magnetotelluric sounding profiles in central Guangxi area, the authors have studied the geological structure of central Guangxi depression and its surrounding areas. Central Guangxi depression is divided into four sub-units, i.e., northern slope, western slope, central depression and eastern slope. The depression was developed on the basis of lower Paleozoic epimetamorphic rock series, and the average thickness of Devonian strata reached 4 000 m. The electrical characteristics show that the Middle-Lower Devonian strata constitute the main horizon of the biogenic reef, and the electricity is characterized by relatively stable low resistance. Two-dimensional inversion of the section has revealed an electrical anomalous body with the character of "high in low", which is inferred to be a reef. Brachyanticlines are well developed in the central depression, and hence the central depression and its surrounding areas are considered to be favorable areas for oil and gas exploration.

1. Institute of Information Geophysical Engineering, Central South University, Changsha 410083, China; 2. No. 814 Geological Party, East China Bureau of Nonferrous Metal Geological Exploration, Zhenjiang 212005, China; 3. China Nonferrous Metals Resource Geological Survey Center, Beijing 100073, China

通过桂中坳陷两条大地电磁测深剖面研究桂中坳陷及周边的地质结构。对构造单元及断层组合特征及古生物礁显示的分析结果显示:坳陷可划分为北部斜坡、西部斜坡、中部凹陷、东部斜坡四个次级构造单元;坳陷是下古生界浅变质岩基底上发育起来,泥盆系平均达4 000 m;泥盆系中下统是古生物礁发育的主要层位,电性特征总体表现为相对稳定的低阻,二维反演断面中发现低中显高的电性异常体,推测为古生物礁;中部凹陷背斜十分发育,中部凹陷及其边缘是油气勘探远景区。

2015

0.0

姚大为, 朱威, 王大勇, 等. 音频大地电磁法在武山外围深部勘查中的应用[J]. 物探与化探, 2015, 39(1): 100-103.

According to the geological background, metallogenic conditions and petrophysical characteristics in the surveyed area, three-dimensional geological mapping was studied by Audio-frequency Magnetotellurics Method (AMT). Based on AMT raw data processing and inversion interpretation, the authors inferred the underground resistivity differences of lithology and fracture structure within 2 km from the contact zone. Combined with the geological data and drilling results, the authors hold that the audio magnetotelluric method is good for detecting the underground geological body, clearly recognizing the marker bed of geoelectric layer and its hierarchical structure.

1. National Center of Geological Exploration Technology, Institute of Geophysical and Geochemical Exploration, CAGS, Langfang 065000, China; 2. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China

根据长江中下游九瑞矿集区武山外围地区的区域地质背景、成矿条件和岩石物性特征,在该区开展音频大地电磁测深法(AMT)的剖面性测量研究.首先对AMT原始时间域数据进行平移去噪、线性插值拟合去噪和应用经验态分解去噪,从而达到消除噪声,还原数据真实地电信息的目的,然后通过傅氏变换将时间域数据转换成频率域数据,再对频率域数据进行二维反演解释,推测了地下2 km以内的电阻率差异较大的岩性接触带和断裂构造.结合该区的地质资料和钻探结果,二维反演结果表明音频大地电磁法能够很好地探测地下目标地质体,清晰划分出标志性地电层及其分层结构.

2013

0.0

杨学明, 苏永军, 杜东, 等. 音频大地电磁法在海水入侵动态监测中的应用[J]. 物探与化探, 2013, 37(2): 301-305.

Through a comprehensive study of the results of dynamic monitoring exploration for seawater in Laizhou Bay by AMT method and other original data, the authors acquired further understanding of the present situation of seawater invasion inside the study-area. Moreover, the authors divided the interface zones between the salt and the fresh water, which resulted in favorable effects of environmental geology. The results indicate that the AMT(EH-4) method is effective in determining the interfaces between the salt and the fresh water, delineating the infection tunnel of seawater and observing the regularity of interface migration.

1. Tianjin North China Geological Exploration Bureau, Tianjin 300170, China; 2. Tianjin Institute of Geology and Mineral Resources, Tianjin 300170, China

通过音频大地电磁法在莱州湾地区海水动态监测勘查中的应用成果,结合原有资料的综合研究,对研究区海水入侵现状,有了进一步的认识,并对咸淡水界面进行了详细的划分,取得了良好的环境地质效果。表明EH-4连续电导率成像系统在圈定海水侵染通道,确定咸、淡水界面及监测界面运移规律监测工作中的有效性。

2011

0.0

武毅, 封绍武, 王亚清. 应用大地电磁法TE、TM模式勘查构造裂隙水[J]. 物探与化探, 2011, 35(3): 329-332.

Groundwater in the bedrock mountain area is mainly structural fissure water. As development of the mountain structural fissures has no direction and is easily impacted by terrain conditions, some conventional geophysical technologies have their limitations, which adversely affects the prospecting result. Based on a study of both "TM" and "TE" observation mode response characteristics by the audio magnetotelluric sounding method, the authors have found that the comparative application of two observation modes can obviously lead to know the anisotropy of strata, with the TE observation mode showing better performance in identifying the spatial distribution of structures. Through the practice application in Taihang Mountain area, the availability of the technique has been verified, thus providing supporting technology for the prospecting of structural fissure water in mountain areas.

1. Center for Hydrogeology and Environmental Geology, CGS, Baoding 071051, China; 2. Qinhuangdao Mineral Resource and Hydrogeological Party, Qinhuangdao 066001, China

基岩山区地下水类型以构造裂隙水为主,而山区构造裂隙发育具有各向异性以及容易受地形影响的特点。为此,研究了大地电磁测深法TM、TE两种观测模式的响应特征,认为通过这两种观测模式的对比应用,可以清晰地了解地层的各向异性,且TE观测模式在识别构造空间分布特征方面更具有突出的优势。在太行山区的实际应用验证了该技术的有效性,为山区构造裂隙水的勘查提供了新的技术支撑。

1992

0.0

... 在电磁探测理论中,电导率和磁导率是两种重要的岩石物性参数^[6] ...

0.0

... Fraser^[7]、Thoms^[8]等人分别研究了航空电磁信号中的磁化率响应 ...

1997

0.0

... Fraser^[7]、Thoms^[8]等人分别研究了航空电磁信号中的磁化率响应 ...

2005

0.0

李学民, 曹俊兴. 磁化率对大地电磁响应的影响研究[J]. 地球物理学报, 2005, 48(4): 947-950.

In the case that the susceptibility of material is greater than that of free space, we deduce the forward modeling formula of 2_D magnetotelluric with resisitivity and magnetic susceptibility as model parameters. Using the finite difference method we calculate the distribution of the electromagnetic field. We analyze the influence of the magnetic susceptibility on MT responses in detail and confirm that it mainly affects in_phase components of the magnetic field and hardly affects both the quadrature components and the electric field components. When the magnetic susceptibility is κ≥001, the apparent resistivity may increase by about 5Ωm at some low frequencies, and the amplitudes of change increase observably with growing magnetic susceptibility. Furthermore, magnetic susceptibility has little effect on impedance phase. In a word, this study provides a new study idea to interpret the observed MT data in areas of high magnetic susceptibility.

State Laboratory of Oil/Gas Reservoir Geology and Exploitation,Chengdu University of Technology, Chengdu 610059, China

本文推导了物质的磁化率大于自由空间的情况下的二维大地电磁(MT)正演计算公式. 利用有限差分法实现了其正演计算，获得了电磁场的分布. 详细地讨论了磁化率对MT响应的影响，证实了磁化率主要影响磁场信号的同相分量，而对磁场信号的异相分量和电场信号的影响比较弱. 当磁化率κ≥001时，在某些低频点的视电阻率值可以增加5Ωｍ左右，并且随着磁化率增加，这种增加的幅度显著增大；而对阻抗相位的影响则非常小. 新的认识为高磁化率物质存在的地区观测到的MT数据解释提供一种新的研究思路.

... 李学民^[9]认为磁化率主要影响大地电磁磁场的同相分量,对磁场的异相分量及电场影响较弱 ...

2014

0.0

刘应冬, 谭捍东, 宋文杰. 磁化率参数对大地电磁响应的影响研究[J]. 地球物理学进展, 2014, 29(5): 2040-2046.

Conventional magnetotelluric data processing method is generally assumed that the underground medium is nonmagnetic, but susceptibility is also an important parameter of rock and minerals. In this paper, we use finite element method to simulate the two-dimensional magnetotelluric forward as an example, analyzing the influence of permeability parameters on the response of different geological model.The results showed that: the magnetotelluric data includes susceptibility parameters where a magnetic geology body underground, the magnitude of this effect increases with magnetic susceptibility increases. By comparing different models shows that the TM mode forward response was stronger than TE mode in the variations of susceptibility, the high resistivity body is more sensitive than the low one. There is provide a new approach to apply MT data effectively and reduce the geophysical multiple solutions problem in magnetic geological areas by the study of forward and inversion upon the susceptibility parameters.

1. Institute of Multipurpose Utilization of Mineral Resources, Chinese Academy of Geological Sciences, Chengdu 610041, China; 2. China University of Geosciences, Beijing 1000834, China; 3. Shandong Institute of Earthquake Engineering, Jinan 250014, China

常规的大地电磁数据处理方法一般假定地下介质是无磁性的,但磁化率也是岩(矿)石的重要参数之一.本文推导了磁化率的二维正演公式,应用有限单元法实现正演模拟,建立不同地质模型,分析研究磁化率参数对正演响应的影响规律.结果表明:当地下地质体具有磁性时,大地电磁数据包含有磁化率参数的影响,随着磁化率的增大,这种影响的幅度相应增大,磁化率参数对TM模式的正演响应影响强于TE模式,高阻地质体比低阻体对磁化率更加灵敏. 磁化率参数的正反演研究,对有磁性地质体地区的MT数据的有效应用和减小地球物理多解性问题据提供了新的依据.

... 刘应冬^[10]研究认为高阻地质体中较低阻体对磁化率反应更加灵敏 ...

0.0

... 在磁化率参数提取方面,Zhang^[11]在假设电阻率分布已知的情况下,利用频率域的电磁数据进行磁化率一维反演 ...

1998

0.0

... Beard^[12]尝试利用航空电磁信号同时反演电阻率参数和磁化率参数 ...

0.0

... Zhang^[13]实现了利用单一数据同时反演一维电阻率和磁化率的算法 ...

2003

0.0

... Fqarhuasro^[14]在反演中引入磁化率对数约束,对线圈电磁数据进行了电阻率和磁化率一维反演 ...

... 同时为保证磁化率为正,引入磁化率对数约束^[14,30] ...

2003

0.0

... 李学民^[15]采用带限约束的迭代方法进行了电阻率和磁化率反演研究,并应用于火山岩分布区地质构造勘查 ...

... 具有相乘的关系,因而同时反演问题是一个非线性问题^[15] ...

2006

0.0

... (500 ~2 000 m)内的矿产勘探,具有一定的意义^[16] ...

2005

0.0

... 磁感应强度B与磁场强度H关系^[17]为B=#cod#x003bc ...

1990

0.0

... 朴化荣^[18]指出岩矿石的相对磁导率与铁磁性矿体积含量有关,认为沉积岩的#cod#x003bc ...

2003

0.0

... _r可以达到5^[19] ...

1994

0.0

... 根据麦克斯韦方程,可推导得到z方向电磁场E_z和H_z满足的偏微分方程^[20]: ...

2015

0.0

... 的积分分解为对各单元e的积分之和,单元内部采用双线性插值方法进行插值,采用定带宽存储方式进行总体系数矩阵的组装^[21] ...

2013

0.0

冯兵, 王珺璐, 王玉, 等. 利用CSAMT电磁场响应提取激电效应的方法初探[J]. 地球物理学进展, 2013, 28(4): 2116-2122.

In the traditional forward modeling of CSAMT electromagnetic, simulate the polarized ground CSAMT electromagnetic response by adding Cole-Cole model. Based on the theoretical calculation of homogeneous half space and H Model geoelectric section, we analysis the effect characteristics of Ex, Hy of CSAMT, which are impact by Cole-Cole model parameters. Based on the electric field relative to the magnetic field of the IP effect reflects more sensitive, we have proposed a method which using Hy and Ex components to inverse the resistivity, thickness and induced polarization parameters. The inversion calculations show this method overcomes the big influence by the initial model and the problem of the calculation is easy to fall into local minimum when the inversion using the resistivity, thickness, induced polarization parameters. Certain extent, we can extract the appropriate IP parameters.

Chang'an University, Xi'an 710054, China

在传统的CSAMT电磁场一维正演中加入柯尔-柯尔模型,模拟可极化地电断面的CSAMT电磁场响应.通过对均匀半空间、H型地电断面的理论计算,分析了柯尔-柯尔模型参数对CSAMT的 Ex、Hy 影响特征.基于电场相对磁场对激电效应的反映更加灵敏,提出分别利用 Hy 与 Ex 分量反演电阻率、厚度以及激电参数的方法.反演计算表明,该方法克服了电阻率、厚度、激电参数一同反演时受初始模型影响太大,容易陷入局部极小值的问题,可以在一定程度上提取出合适的激电参数.

... 3 磁化率参数的提取目前,从电磁信号中提取电性参数时一般采用反演的方法^[22] ...

2007

0.0

于鹏, 王家林, 吴健生, 等. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 2007, 50(2): 529-538.

Joint inversion is an important quantitative interpretation tool for integrated geophysics. We first review and analyze the current state of the research and progresses of joint inversion using gravity and seismic data. Then, we employ the improved very fast simulated annealing algorithm (VFSA), which has obvious advantage of finding overall optimal solution in inverse problems, to perform constrained synchronous joint inversion of gravity and seismic data. This inversion uses a designed model with uncommon interface of density and velocity. Through the model test and field observed data processing and interpretation, this method is proved effective and practicable, especially the application in the Xuwen area shows that the density and velocity structures of the underground complicated interfaces could be exactly determined and revealed. With constrained known information, this joint inversion method is clearly superior to the single inversion of gravity data.

State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092,China

联合反演是综合地球物理研究的重要定量解释手段.本文在总结和分析重力与地震资料联合反演的研究现状基础上,利用改进的全局寻优的快速模拟退火算法,实现了重力和地震资料的约束同步联合反演.针对性地设计了密度和速度界面不完全一致的模型,理论模型的试验说明了方法的效果和适用性.结合最近完成的广东徐闻地区实际资料的处理和解释,表明该方法可准确确定复杂构造物性界面的密度和速度结构,在该地区的油气勘探中发挥了作用.在先验信息约束下,该联合反演方法要明显优于单独的重力反演.

... 1 改进的模拟退火算法模拟退火算法(SA)及相应的改进算法是解决非线性反演问题的重要方法,该方法不用求目标函数的偏导数,不用解大型矩阵方程组,即能找到一个全局最优解,而且易于加入约束条件^{[23,24,25,26]} ...

2007

0.0

1998

0.0

2002

0.0

杨辉, 王家林, 吴健生, 等. 大地电磁与地震资料仿真退火约束联合反演[J]. 地球物理学报, 2002, 45(5): 723-734.

In this paper the continuous model space of the very fast simulated annealing was transformed to a variable discrete. It can be proved by theoretical models that 5 to 10 times calculation workload can be saved. In order to fit the needs of joint inversion, the 'single judge' rule in the error checking of the very fast simulated annealing algorithm was developed to the 'double judge' rule to avoid the judge mistakes made by Metropolis accepting rule. One dimensional and two dimensional multi parameters joint inversion of magnetotelluric and seismic data were put forward under the uneven topography conditions. The example calculation results of the theoretical models and real observed data illustrated that this constraint joint inversion technique was quite effective.

1. Laboratory of Marine Geology, MOE, Tongji University, Shanghai 200092, China; 2. University of Petroleum, Beijing 102200, China; 3. Bureau of Oil Geophysical Prospecting, CNPC, Zhuozhou 072751, China

在对仿真退火算法研究的基础上,将非常快速仿真退火的连续模型空间改为可变的离散化形式,理论模型试算表明,使用本文方法可提高工作效率5-10倍. 为适应联合反演的需要, 对非常快速仿真退火的误差"单判断"检验准则改为误差"双判断"检验准则,避免Metrop olis接受准则的判断失误. 在此基础上,实现了一维及二维起伏地形条件下大地电磁与地震资料多参量信息的联合反演. 理论模型的试算及实例说明了约束联合反演的有效性.

2002

0.0

... 笔者采用陈华根^[27]提出的改进的特别快速模拟退火(MVFSA)算法开展电阻率与磁化率参数的同时反演 ...

2008

0.0

李帝铨, 王光杰, 底青云, 等. 基于遗传算法的CSAMT最小构造反演[J]. 地球物理学报, 2008, 51(4): 1234-1245.

We apply Genetic Algorithm to invert CSAMT data. Here, we invert both apparent resistivity and phase data which contain the near-field, transition zone field and the far-field without any correction. Genetic Algorithm is one kind of global optimization method with less dependence on initial model and more ability to find the best solution, but when the unknowns are too many then the non-uniqueness of solution is still a problem. When we use a multi-layer model in the inversion CSAMT does not yield a unique solution. In order to reduce the temptation to over interpret the data and to eliminate arbitrary discontinuities in simple layered models, we employ minimum structure to constrain the inversion result. We have defined minimum structure function for the CSAMT inversion based on genetic algorithm, and have found the optimal value of the Lagrange multiplier μ =0.5. The designed models are H, A, K, Q and HKH, KHA. When the data is without noise or with 10% noise, the resulting resistivity models fit the true models well. When the data contains 20% noise, the inversion result is also good. The method has been used for field data processing, the result was good. Both synthetic and field data examples indicate that the method is effective.

Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China

利用遗传算法进行不考虑近场校正的全场资料CSAMT反演研究.遗传算法属于全局最优化方法，具有对初始模型依赖小，不易陷入局部极值的优点，然而，当未知数较多时，多解性仍是该方法的瓶颈.为了减小多层反演的多解性，在反演中引入最小构造约束，针对CSAMT的遗传算法反演问题定义了最小构造目标函数，经过模型试验找到了其具体表达式，并找到了适合CSAMT资料反演的拉格朗日乘子的最佳取值 μ =0.5，实现了基于遗传算法的CSAMT最小构造反演.利用H、A、K、Q和HKH、KHA模型对方法进行了数值试验，在无噪和加入10％噪声情况下，反演结果与模型一致；加入20％噪声后，反演仍取得良好结果，与理论模型基本吻合.将该方法用于水平层状地层和横向变化地层的实测资料反演，结果与地质资料吻合.不同的计算实例表明了该方法的有效性.

... 进行电阻率与磁化率同时反演时,采用最小构造思想^[28,29],引入电导率与磁化率光滑约束 ...

2011

0.0

... 进行电阻率与磁化率同时反演时,采用最小构造思想^[28,29],引入电导率与磁化率光滑约束 ...

2003

0.0

... 同时为保证磁化率为正,引入磁化率对数约束^[14,30] ...