基于稀疏反演算法的高分辨率Radon变换及其在多次波压制中的应用

引用本文

范景文, 李振春, 刘学通, 刘玉金, 张凯. 基于稀疏反演算法的高分辨率Radon变换及其在多次波压制中的应用[J]. 物探与化探, 2017,39(6): 1245-1250.
FAN Jing-Wen, LI Zhen-Chun, LIU Xue-Tong, LIU Yu-Jin, ZHANG Kai. High-resolution Radon transform based on sparse constraint method and its application to multiple attenuation[J]. Geophysical and Geochemical Exploration, 2017,39(6): 1245-1250. 复制到剪切板

Doi:10.11720/wtyht.2015.6.24
Permissions

《物探与化探》编辑部

基于稀疏反演算法的高分辨率Radon变换及其在多次波压制中的应用

范景文¹, 李振春¹, 刘学通², 刘玉金¹, 张凯¹

1.中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

2.中海石油(中国)有限公司天津分公司,天津塘沽 300452

作者简介: 范景文(1991- ),男,硕士在读,就读于中国石油大学(华东),目前从事地球物理处理相关研究工作。

收稿日期: 2015-02-11

基金: 国家自然科学基金课题(41204086); 国家重点基础研究发展计划(973计划)课题(2011CB202402); 国家科技重大专项课题 (2011ZX05023-004-001 )联合资助

摘要

针对目前双曲Radon变换Radon域能量团能量泄漏的问题,提出一种基于稀疏约束反演算法的高分辨率Radon变换进行多次波的压制。该方法在常规双曲Radon变换的基础上加入稀疏约束条件,应用共轭导向梯度(CGG)反演算法进行求解,能有效地提高Radon域速度谱的聚焦效果,有利于分离一次波和多次波。模型和实际资料试算证明了该方法的有效性和实用性。

关键词: 稀疏反演; Radon变换; CGG反演算法; 多次波压制

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)06-1245-06

High-resolution Radon transform based on sparse constraint method and its application to multiple attenuation

FAN Jing-Wen¹, LI Zhen-Chun¹, LIU Xue-Tong², LIU Yu-Jin¹, ZHANG Kai¹

1.School of Geoscience and Technology,China University of Petroleum (East China),Qingdao 266580,China

2.Tianjin Branch,CNOOC China Co.,Ltd.,Tianjin 300452,China;

Abstract

In view of the problem of the Radon domain energy group energy leakage,this paper proposes a multiple attenuation method based on high-resolution Radon transform.The authors employed sparse constraint operator on the basis of conventional hyperbolic Radon transform,which can improve the degree of focus of velocity spectrum and better separate effective and multiple energy groups.Model and real data tests show that the proposed method is effective and applicable.

Keyword: sparse inverse; Radon transform; CGG inversion method; multiple attenuation

Show Figures

在众多的多次波压制方法中, 基于Radon变换的多次波压制方法有较高的计算效率, 已经得到了广泛应用。Radon变换利用多次波和一次波的速度差异, 将时空域数据变换到Radon域, 进行多次波的识别以及压制消除(如滤波或者预测反褶积等操作), 并最终得到时空域的处理结果^{[1, 2, 3, 4, 5, 6, 7, 8]}。

常规Radon变换是应用最小二乘反演方法或者通过Levinson递推法来尽可能的接近它的逆。为了保证反演过程的稳定性, 常规的做法是引入阻尼正则化算子。但是阻尼约束条件假定模型符合高斯分布, 因此会导致Radon变换的分辨率较低, 不利于有效信号和干扰信号的分离。高分辨率Radon变换是在L₁模或Cauchy模的意义下对模型空间进行稀疏约束, 以更好地聚焦一次波和多次波能量团, 在不损失有效信号的基础上, 在变换域去除多次波成分对应的能量团, 最后通过反变换到数据空间得到去除多次波后的地震记录^{[9, 10, 11, 12, 13, 14, 15]}。

此次研究主要在稀疏反演的理论框架下实现高分辨率Radon变换, 改善Radon变换速度谱的聚焦效果, 从而达到更好地压制多次波的目的, 为后续的地震成像、反演解释、钻井定位等提供数据基础。

1 Radon变换的基本理论

根据积分路径的不同, 可以把Radon变换分为线性、抛物线型、双曲线型Radon变换。线性Radon变换就是对数据进行倾斜叠加, 是其中的一种特例, 常用来去除具有线性特点的干扰波, 如声波等。抛物型Radon变换常用于部分动校正后的地震记录上, 对于动校正后的记录与有效波波场存在较大时差的情况, 比如去除多次波; 但是对于远偏移距的记录不能得到正确的旅行时信息, 会导致反射同相轴得不到较好的近似值, 因此计算精度受到限制^[5]。为提高变换的准确率, 实际中常把CDP道集叠加看成是双曲线叠加, 在时间— 偏移距域进行时变速度叠加。在时间— 速度域去除多次波能量团达到分离多次波和一次波的目的, 即双曲线Radon变换。

地震学中常常将Radon变换定义为

$\begin{matrix} u (τ, p) = \overset{+ \infty}{\int_{- \infty}} d (t, h) dh, (1) \end{matrix}$

式中:d(t, x)为时间域地震数据; u(τ , p)表示Radon域的数据值; h为空间变量值, 2D空间时表示x方向的偏移距信息; p表示曲线的曲率; τ 为时间轴的截距值; t为双程旅行时间值。当t= $\begin{matrix} \sqrt{τ^{2} + p^{2} h^{2}} \end{matrix}$ 时, 就是双曲型Radon变换。将双曲积分算子代入式(1)并离散化, 可得到

$\begin{matrix} u (τ, p) = \overset{x_{\max}}{\sum_{x = x_{\min}}} d (t^{2} = τ^{2} + x^{2} p^{2}, x), (2) \end{matrix}$

相应的共轭变换形式为

$\begin{matrix} d (t, x) = \overset{p_{\max}}{\sum_{p = p_{\min}}} u (τ^{2} = t^{2} - x^{2} p^{2}, p) 。 (3) \end{matrix}$

2 稀疏反演算法

由于计算中需要进行离散, Radon变换会产生截断效应, 在传统最小二乘意义下计算求解的Radon变换不能有效地压制这种效应。此外, 野外地震数据采集时采集孔径有限以及地震数据缺失, 常规的Radon变换域内一次波和多次波对应的能量团, 因能量泄漏存在着明显的剪刀状效应。通过对模型加入稀疏约束条件, 可以大大地提高反演结果的分辨率, 提高能量团的聚焦效果。图1a、b是常规及加入稀疏约束条件的高分辨率Radon变换示意, 后者得到的慢度谱可以较好地抑制能量泄漏效应。

	Figure Option View Download New Window
	图1 常规及高分辨率Radon变换对比

Radon变换的离散形式可以用d=Lm的矩阵形式表示, 常规最小二乘解得到的Radon变换的分辨率有限, 因此考虑引入稀疏约束条件提高速度谱的聚焦程度。目标函数

$\begin{matrix} J = ‖ d - Lm ‖_{2}^{2} + λR (m), (4) \end{matrix}$

式中:等式右面第一项是常规反演的目标表达式; R(m)表示稀疏约束项; λ 表示正则化参数, 用来调节约束项与观测数据误差L₂范数之间的权重, 一般在资料处理中λ 的选取应通过实验的方法获得。引入以下几个参数:W_d是数据加权矩阵, 通常是对角矩阵, 包括数据标准偏差的逆; W_m是模型加权矩阵, 可以自己设计用以提高模型拟合度, 一般由先验信息来确定, 如分辨率和平滑因子; P表示观测向量模值的范数。

求解方程

$\begin{matrix} (λ W_{m}^{T} W_{m} + L^{T} W_{d}^{T} W_{d} L) m = L^{T} W_{d}^{T} W_{d} d (5) \end{matrix}$

就能得到抗噪性较好的稀疏解。其中:diag(W_d)_i=|r_i|⁽^p-²⁾^/², diag(W_m)_i=|m_i|⁽²^-p⁾^/²。当W_d=I并且W_m=I, 即约束矩阵都是单位矩阵时, 上述方程退化为求解最小二乘解的问题。常规Radon变换应用常规共轭梯度(CG)算法进行求解, 高分辨率Radon变换则应用共轭导向梯度(CGG)^[16]反演方法, 可以得到较好的稀疏解, 如表1、表2所示。

表1 常规CG算法

表2 CGG算法

共轭导向梯度算法
r⇐Lm-d; 迭代{ diag(W_r)⇐f(r), diag(W_m)⇐f(m); Δ m⇐ $\begin{matrix} W_{m}^{T} \end{matrix}$ L^T $\begin{matrix} W_{r}^{T} \end{matrix}$ r; Δ r⇐LΔ m; (m, r)⇐cgstep(m, r, Δ m, Δ r); }

表2 CGG算法

CGG算法是在迭代加权最小二乘(IRLS)算法的改进基础上形成的。IRLS是在传统最小二乘方法中引入剩余量加权函数f(r)和模型加权函数f(m), f(r)=diag(w_r)_i=|r_i|⁽^p-²⁾^/², f(m)=diag(w_m)_i=|m_i|⁽²^-p^)/2, 这样剩余量可以表示成r⇐W_r(LW_mm-d), 该算法有两层循环, 外层循环对加权系数迭代更新, 内层循环对加权后的算子进行最小二乘共轭梯度求解。为避免IRLS算法产生的非线性求解问题, CGG算法不改变修改算子, 而是引导搜索方向在特定的模型子空间中寻找满足需求的解, 与传统共轭梯度算法的不同之处在于梯度的计算。不管从数据拟合剩余量还是模型剩余量的角度修改梯度, 该算法都仅仅修改了梯度方向。显然, 常规共轭梯度算法没有进行稀疏加权, 分辨率有限, 能量团聚焦效果较差。因此文中选取CGG算法进行高分辨率Radon变换的求解。在CGG算法实现过程中, p值可根据我们希望解决的问题选取, 当p值为1时, 为了避免剩余加权函数f(r)中元素分母为零的情况, 还应引入阻尼参数ε , ε 可取值为ε =max|d|/100, 本文中p取1^[16]。

3 模型和实际资料测试

3.1 2D模型测试

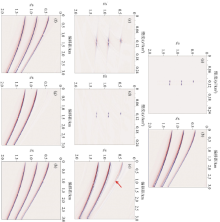
为验证上面的反演算法, 首先进行2D模型测试, 图2a中左面三个子波代表一次波慢度成分, 右面两个子波代表多次波慢度成分; 图2b表示合成的地震记录; 图2c、d分别表示应用常规和高分辨率Radon变换均迭代20次求解得到的结果, 显然图2d得到的聚焦效果更好, 基本消除了剪刀状效应; 图2e、f分别表示应用常规Radon变换分离出来的多次和一次波成分, 图2g、h分别表示应用高分辨率Radon变换分离出的多次和一次波成分, 对比可以看出, 常规Radon变换分离出的多次波含有一次波成分(图2e中红色箭头所示), 图2g分离出的多次波基本不包含一次波成分, 即分离的效果更好。

	Figure Option View Download New Window
	图2 2D模型测试(a— 慢度谱模型; b— 合成地震记录; c— 常规Radon变换的得到的慢度谱; d— 高分辨率Radon变换得到的慢度谱; e— 常规Radon变换分离出的多次波; f— 常规Radon变换分离出的一次波; g— 高分辨率Radon变换分离出的多次波; h— 高分辨率Radon变换分离出的一次波)

3.2 3D模型测试

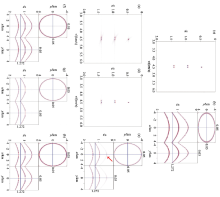
将2D测试拓展到3D空间。图3a表示合成的3D地震记录, 左面表示两个子波表示多次波的速度成分, 右面三个子波表示的是一次波的速度成分; 图3b是合成的地震记录; 图3c、d分别为应用常规Radon变换和高分辨率Radon变换得到的速度谱, 对比两图可知, 常规Radon变化存在的剪刀状效在高分辨率Radon变换中基本消除了; 图3e、f分别表示应用常规Radon变换分离出来的多次和一次波成分; 图3g、h分别表示应用高分辨率Radon变换分离出的多次波和一次波成分。由图3e、g对比可知, 在图3e中常规Radon变换分离出的多次波含有一次波成分(图中红色箭头所示), 而图3g中高分辨率Radon变换分离出的多次波不含一次波成分, 因此可知, 高分辨率Radon变换更有利于多次波的压制。

	Figure Option View Download New Window
	图3 3D模型测试(a— 速度谱模型; b— 合成地震记录; c— 常规Radon变换的得到的速度谱; d— 高分辨率Radon变换得到的速度谱; e— 常规Radon变换分离出的多次波; f— 常规Radon变换分离出的一次波; g— 高分辨率Radon变换分离出的多次波; h— 高分辨率Radon变换分离出的一次波)

3.3 实际资料测试

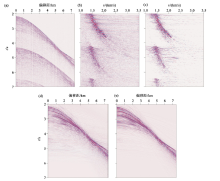
图4是海上某探区实际测试效果对比。图4a是原始CMP道集, 共有599道, 道间距为12.5 m, 第一道偏移距为185 m, 最大偏移距为7 660 m, 时间采样间隔为2 ms, 采样长度为7 s, 从CMP道集可以看出, 该数据多次波发育较好, 利用t₀时间识别多次波可知, 原始CMP道集中存在二次反射波和三次反射波, 该多次波为海上表层多次波; 图4b、c是对图4a作常规Radon变换和高分辨率Radon变换迭代20次后求解得到的速度谱, 从图中可以看出图4c速度谱更加聚焦, 更有利于分离一次波和多次波; 图4d、e分别是对图4b、c切除多次波后并反变换得到的CMP道集, 对比可知后者恢复的一次波信息效果较常规方法有了明显的改善。

	Figure Option View Download New Window
	图4 海上某探区实际资料测试(a— CMP道集; b— 常规Radon变换的速度谱; c— 高分辨率Radon变换的速度谱; d— 对图4b切除多次波并反变换得到的CMP道集; e— 对图4c切除多次波并反变换得到的CMP道集)

4 结论

1)在基于常规CG反演的Radon变换算法的基础上, 实现了基于CGG算法的高分辨率Radon变换, 并且将该算法拓展到3D空间。模型和实际资料测试表明该算法的计算精度得到了提高。

2)基于时变算子的双曲Radon变换不能在F-X域求解, 因此如何解决时间域大型矩阵求逆的计算效率以及解决三维实际资料的适用性是需要进一步研究的工作。

3)为进一步提高信号域滤波的计算精度, 可以考虑在其他成像道集上进行上述变换, 如共散射点道集、共成像点道集等等。

致谢:感谢中国石油大学(华东)地震波传播与成像课题组的老师和师兄师姐在本文写作过程中的大力指导。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cary P W. The simplest discrete radon transform[C]//Expand ed Abstracts of 68^th SEG Annual Internet Meeting, 1998. [本文引用:1]
[2]	Ethan J N, Matthias G I. Amplitude preservation of Radon-based multiple-removal filters[J]. Geophysics, 2006, 71(5): 123-126. [本文引用:1]
[3]	Hampson D. Inverse velocity stacking for multiple elimination[C]//Expand ed Abstracts of 56^th SEG Annual Internet Meeting, 1986, 422-424. [本文引用:1]
[4]	Douglas J F, Charles C M. Suppression of multiple reflections using the Radon transform[J]. Geophysics, 1992, 57(3): 386-395. [本文引用:1]
[5]	熊登, 赵伟, 仗剑锋. 混合域高分辨率抛物Radon变换及其在衰减多次波中的应用[J]. 石油地球物理学报, 2009, 52(4): 1068-1077. [本文引用:2]
[6]	刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. [本文引用:1]
[7]	朱生旺, 魏修成, 李峰, 等. 用抛物radon变换稀疏解分离和压制多次波[J]. 石油地球物理勘探, 2002, 37(2): 110-115. [本文引用:1]
[8]	吴律. τ-p变换及其应用研究[M]. 北京: 石油工业出版社, 1993. [本文引用:1]
[9]	Sacchi M D, Ulrych T J. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60: 1169-1177. [本文引用:1]
[10]	Trad D O, Ulrych T J, Sacchi M D. Accurate interpolation with high-resolution time-variant radon transforms[J]. Geophysics, 2002, 67: 644-656. [本文引用:1]
[11]	Liu Y J, Peng Z, Symes W W, et. al. Sparse Radon transform with dual gradient ascent method[C]//Expand ed Abstracts of 83^rd SEG Annual Internet Meeting, 2013, 4650-4655. [本文引用:1]
[12]	巩向博. 高精度Radon变换及其应用研究[M]. 长春: 吉林大学, 2008. [本文引用:1]
[13]	Cristina M C, Sacchi M D. Enhanced resolution in Radon domain using the shifted hyperbola equation[C]//Expand ed Abstracts of 75^th SEG Annual Internet Meeting, 2005. [本文引用:1]
[14]	Trad D, Ulrych T, Sacchi M. Latest views of the sparse radon transform[J]. Geophysics, 2003, 68: 386-399. [本文引用:1]
[15]	Beylkin G. Discrete radon transform: Acoustics, Speech and Signal Processing[J]. IEEE Transactions on, 1987, 35: 162-172. [本文引用:1]
[16]	Ji J. Cgg method for robust inversion and its application to velocity-stack inversion[J]. Geophysics, 2006, 71(4): R59-R67. [本文引用:2]
[17]	刘玉金, 李振春, 黄建平. 基于共散射点道集的高分辨率混合Radon变换多次波压制方法研究[C]//中国地球物理年会第27届年会, 2011. [本文引用:1]
[18]	宋翔宇, 李振春, 周卿, 等. 共散射点道集映射噪音压制方法及应用[J]. 石油物探, 2013, 52(5): 524-529. [本文引用:1]
[19]	张凯. 叠前偏移速度分析方法研究[D]. 上海: 同济大学, 2008. [本文引用:1]
[20]	李振春, 李志娜, 郭书娟, 等. 数据域与成像域多次波压制方法对比[J]. 地球物理学进展, 2013, 28(6): 2901-2910. [本文引用:1]
[21]	Sava P, Guitton A. Multiple attenuation in the image space[J]Geophysics, 2005, 70(1): V10-V20. [本文引用:1]

1998

0.0

... Radon变换利用多次波和一次波的速度差异,将时空域数据变换到Radon域,进行多次波的识别以及压制消除(如滤波或者预测反褶积等操作),并最终得到时空域的处理结果^{[1,2,3,4,5,6,7,8]} ...

2006

0.0

1986

0.0

1992

0.0

2009

0.0

熊登, 赵伟, 仗剑锋. 混合域高分辨率抛物Radon变换及其在衰减多次波中的应用[J]. 石油地球物理学报, 2009, 52(4): 1068-1077.

There are two alternative choices for either efficiency or resolution in today′s high-resolution Radon transform algorithms. Time-domain high resolution Radon algorithm confronts serious efficiency degeneration while maintains much higher resolution than any other methods. On the contrary, frequency-domain high-resolution Radon algorithm generally leads to efficient computation at the cost of more smearing and artifacts in Radon domain. To overcome these problems some methods concerning hybrid-domain computation were developed which utilized time-variant sparse weight for frequency domain Radon transform. We propose a new method of the hybrid-domain computation named hybrid-domain high-resolution parabolic Radon transform and use it to suppress multiples for prestack seismic data. Routines for hybrid-domain high-resolution parabolic Radon transform and prestack data demultiple are provided respectively in our paper. Numerical tests of modeling and field data confirm ideal resolution and very high efficiency of our method.

高分辨率Radon变换存在计算效率和分辨率不能兼得的困境.时间域算法可以获得很高的分辨率，但计算效率非常低；频率域算法具有良好计算效率，但分辨率不理想.为此发展了混合域高分辨率抛物Radon变换，即对频率域抛物Radon变换引入时变的稀疏权.本文给出了一种新的混合域高分辨率抛物Radon变换实现方法，并将该算法应用于叠前数据衰减多次波.文中给出了Radon变换和衰减多次波的流程.理论和实际数据算例表明本文方法既有较高的分辨率又有很高的计算效率.

... 但是对于远偏移距的记录不能得到正确的旅行时信息,会导致反射同相轴得不到较好的近似值,因此计算精度受到限制^[5] ...

2004

0.0

刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15.

Radon transformation is employed commonly in seismic data processing, especially in the events identification and estimation. The least square inversion scheme is the most ordinary method to implement the Radon transform, both for slant stack and for general Radon transform. Although many and many study have been made, there are a lot of works needed doing in enhancing the transform revolution and the computation efficiency. In this paper ,Parabolic Radon Transform （PRT） and Hyperbolic Radon Transform（HRT） have been studied by least square inversion .In the implementation of the methods, sparse constraint preconditions conjugate gradient method has been applied for enhancing the resolution. Compared to the damped least square method, the sparse constraint preconditions conjugate gradient method has advantages. This is proved by a synthetic model. On base of the difference of residual move-out between the primary and the multiple reflections, the multiple could be suppressed by Radon transform. The principals and the schemes of the method are presented in the paper with a real example. It shows that the sparse constraint precondition conjugate gradient method is proper for enhancing the Radon transform resolution , the efficiency and the accuracy are very well, and by the algorithm multiple can be suppressed better.

Radon变换方法在地震资料处理中广泛采用,在地震同相轴识别和估计方面具有良好效果.无论是倾斜叠加,还是广义Radon变换方法,一般采用最小二乘反演方法实现.目前,在提高反演算法的效率和分辨率方面仍值得研究.本文从倾斜叠加的定义出发,阐明Radon变换分辨率问题的来源和解决办法.采用最小二乘反演方法研究高分辨率抛物线Radon变换和双曲Radon变换时,给出稀疏约束预条件共轭梯度法求解的高分辨率Radon变换的实现方法,同阻尼最小二乘方法相比,分辨率和精度明显提高,文中给出了模型算例.根据有效波和多次波NMO后剩余时差不同,采用高分辨率抛物线和双曲Radon变换可以压制多次波,分别给出了方法原理,最后给出应用实例.研究表明,稀疏约束预条件共轭梯度法可以有效实现高分辨率Radon变换;数值算例表明,算法计算效率和精度较高,可以更好地实现多次波压制.

2002

0.0

朱生旺, 魏修成, 李峰, 等. 用抛物radon变换稀疏解分离和压制多次波[J]. 石油地球物理勘探, 2002, 37(2): 110-115.

The parabolic Radon transform technique is a currently more used and effectual method for multiples attenuation.But because of limitation of resolution in conventional damping least square solution,fully separating primaries from multiples which have small time difference of normal moveout(NMO)is impossible in a τ-q domain after ransform,so its application can't get satisfied results.The paper presented an improved method which find out sparse solution that has varimax norm along direction of q value in generalized solution which has least square meaning in τ-q domain,so it improves the resolution separating primaries from multiples by using parabolic Radon transform and precisely and effectively fulfils separation and suppression of multiples.Compared with the conventional methods,the improved method has more advantages in a condition of that stack velocity of primaries and multiples has a little cliffcrence and multiples energy,is very strong.Theoretic data test and real data processing proved the effectiveness of the method.

抛物线Radon变换法是目前最常用的、效果较好的一种压制多次波方法。但由于传统的阻尼最小二乘解受分辨率的限制,当动校时差差别较小时,在变换后的 τ-q 域不能完全分离一次波与多次波,从而不能得到满意的结果。为此,本文提出了一种改进方法,即在最小平方意义下的 τ-q 域通解中,找出一种沿 q 值方向具有最大方差模的稀疏解,从而提高了用抛物线Radon变换进行反射波分解的分辨率,更精确、更有效地实现了多次波的分离与压制。与传统的方法相比,在一次波与多次波叠加速度差异较小、多次波能量很强的情况下,本方法表现出较大的优越性。理论数据试算和实际资料处理结果均证实了该方法的有效性。

1993

0.0

1995

0.0

... 高分辨率Radon变换是在L₁模或Cauchy模的意义下对模型空间进行稀疏约束,以更好地聚焦一次波和多次波能量团,在不损失有效信号的基础上,在变换域去除多次波成分对应的能量团,最后通过反变换到数据空间得到去除多次波后的地震记录^{[9,10,11,12,13,14,15]} ...

2002

0.0

2013

0.0

2008

0.0

巩向博. 高精度Radon变换及其应用研究[M]. 长春: 吉林大学, 2008.

本文系统总结了Radon变换各种类型及其基本原理。首先从线性Radon变换出发,用最小平方反演求广义逆介绍了正变换,然后对具有时不变的线性、抛物和多项式Radon变换介绍了它们的频率域Radon变换及其优点,给出了数值解的共轭梯度算法。接着针对离散的Radon变换具有截断效应的不良影响,介绍了可克服这种效应的频率域高分辨率Radon变换,它是把正则化和贝叶斯原理加入到反演之中。最后介绍了适应时变性质的双曲Radon变换的高分辨表象加权Radon变换。总结了离散Radon变换存在的端点效应和截断效应及空间假频等问题。介绍了用高分辨率Radon变换和二维蒙版滤波压制截断效应的方法,对避免空间假频的参数选择进行了讨论。系统地总结了Radon变换的实际用途,包括压制多次波、面波和随机噪声,分离上下行波,及其应用于非规则观测系统的实例。简要介绍了在稀疏道重建,速度分析,偏移成像中的应用。

2005

0.0

2003

0.0

1987

0.0

2006

0.0

... 常规Radon变换应用常规共轭梯度(CG)算法进行求解,高分辨率Radon变换则应用共轭导向梯度(CGG)^[16]反演方法,可以得到较好的稀疏解,如表1、表2所示 ...

... =max|d|/100,本文中p取1^[16] ...

2011

0.0

刘玉金, 李振春, 黄建平. 基于共散射点道集的高分辨率混合Radon变换多次波压制方法研究[C]//中国地球物理年会第27届年会, 2011.

本文提出基于共散射点道集的高分辨率混合Radon变换多次波压制方法，该方法只需要一个初始速度场，就可以对构造条件较为复杂的多次波进行压制，理论模型和实际资料处理验证了该方法的有效性。

2013

0.0

宋翔宇, 李振春, 周卿, 等. 共散射点道集映射噪音压制方法及应用[J]. 石油物探, 2013, 52(5): 524-529.

引入等价偏移距后,可将叠前双平方根旅行时方程改写成单平方根旅行时方程.利用单平方根旅行时方程构建的共散射点(Common Scatter Point,CSP)道集具有提高覆盖次数以及空间反假频等优点;利用它进行速度分析,叠加CSP道集后可以直接得到叠前时间偏移剖面.但在生成CSP道集的过程中存在映射噪声,映射噪声的存在会降低速度拾取的精度,并影响成像效果.在分析CSP道集映射过程中噪声产生机制的基础上,提出了引入振幅校正因子对其进行压制的方法.模型数据和实际资料的试算结果表明,经过噪声压制后的CSP道集和速度谱都有明显的改进,成像质量也得到明显提高.

2008

0.0

2013

0.0

李振春, 李志娜, 郭书娟, 等. 数据域与成像域多次波压制方法对比[J]. 地球物理学进展, 2013, 28(6): 2901-2910.

目前的多次波压制方法按照实现域的不同可分为如下两类，第一类是在数据域实现多次波的压制，该类方法又可分为基于信号处理的滤波法和基于波动理论的预测相减法。基于信号处理的滤波法因其成本低而在工业生产中受到青睐，如Radon滤波去多次波，但是该类方法多次波压制精度较低，对复杂地下适应性差，基于波动理论的预测相减法则可以获得高精度的多次波压制结果，但是是以高计算成本为代价的，如SRME；第二类方法是在成像域实现多次波的压制，该方法可以有效的兼顾多次波压制精度和计算成本。本文首先对数据域与成像域多次波压制几种常用方法的原理进行了简要阐述，在此基础上对这两类方法多次波压制的效果进行了模型试算，通过对比可见这些方法各有所长，近些年发展的成像域多次波压制方法既能精确处理地下复杂的地震波场传播效应，同时又极大的降低了计算量，因此该技术不失为多次波压制技术的一个重要发展方向。

2005

0.0