作者简介: 李俊杰(1989-),江西上饶人,硕士,助理工程师,从事大地电磁无网格化正演研究。Email:lijunjiecsu@163.com
径向基点插值法(RPIM)作为一种高精度的无网格方法,其形函数采用与径向基函数结合的插值方法构造,边界条件可直接加载。将RPIM用于点源二维变分问题的求解,介绍了RPIM的近似原理;推导了点源二维问题的RPIM总体矩阵表达式,简述了背景网格积分技术,研究了高斯点数目对RPIM计算精度的影响;最后通过数值试验得出了支持域无量纲尺寸 α最优选择区间与RPIM形状参数最优值。研究结果表明:RPIM求解点源二维变分问题具有较好的鲁棒性, α最优区间为1.0~1.2。
Radial point interpolation method (RPIM) is a kind of high precision meshfree method. As its shape function is constructed by interpolation method in combination with radial basis function, the boundary conditions can be directly loaded. This paper utilizes RPIM to the calculation of point source two-dimensional electric field. Firstly, the approximate principle of RPIM is introduced in detail and the discrete system matrix expression is deduced corresponding to point source two-dimensional variational problem. Secondly, background grid integral technology is briefly introduced and the influence of different number of gauss points on calculation accuracy of RPIM is discussed. Lastly, the optimal range of support domain dimensionless size and the shape parameter optimal value of RPIM are obtained through numerical experiments. Studies show that RPIM has robustness for solving point source two-dimensional variational problem, and the optimal α range is 1.0 to 1.2.
有限元法(finite element method , FEM
径向基点插值法(Radial point interpolation method, RPIM)相较PIM引入了径向基函数, 改善了PIM插值函数的奇异性, 且该算法支持域无量纲尺寸的选择区间更大, 从而能更好地处理各类工程与科学计算问题。文中以点源二维电场问题为例介绍了RPIM的近似原理, 从点源二维变分问题出发结合Galerkin法推导了总体矩阵的无网格化离散表达式, 最后通过数值计算得出了适用于点源二维正演问题的RPIM支持域无量纲尺寸、高斯点数量及径向基函数形状参数的最优值。
点源为三维源, 需先采用傅里叶变换将三维点源从空间域转化为波数域二维源, 当地下电性结构为二维时, 取走向为z轴, x轴与z轴垂直, y轴垂直向上, 求解域为矩形区域, 4个顶点依次以A、B、C、D逆时针编号, 波数域电位满足变分问题[15]
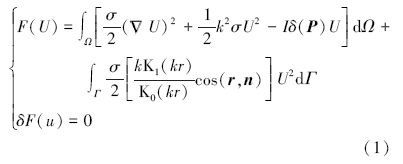
式中: 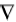
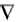
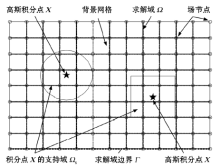
RPIM利用位于积分点支持域内的场节点构造形函数。支持域是人为定义的一个区域, 其形状主要有圆形与矩形两种, 对于节点均匀分布的情况, 支持域尺寸一般取横、纵向节点间距与支持域无量纲尺寸α 之积。α 用于控制实际支持域的大小, 是对无网格法计算精度影响很大的重要参数[13]。图1为RPIM背景网格、支持域、积分点与场节点示意, 由于背景网格的积分常选用高斯积分法, 故积分点又称高斯积分点或高斯点。
求解域Ω 中任意一点X处的场变量U(X)的径向基点插值近似表达式为
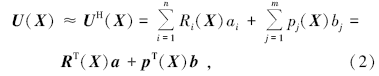
式中:RT(X)为径向基函数(radial basis function, RBF), p(X)为二维空间坐标XT=[x, y]的基函数; a与b是系数向量; n为RBF的个数, m为单项式的个数。常用RBF主要有MQ(multi-quadrics)函数、高斯指数(EXP)函数、薄板样条(thin plate spline, TPS)函数:
式中:dc为与节点间距有关的特征长度, 当节点均匀分布时可取dc=
式(2)的p(X)可用Pascal三角形确定, 其线性基函数为pT(X)=[1 x y], 式(2)简化为
式中:Us=[u1u2u3 … un]T; a=[a1a2a3 … an]T; b=[b1b2b3 … bn]T。R0与Pm的展开式分别为
式(4)中有n+m个变量, 可使用下面m个约束条件添加m个方程
联立式(4)与式(7), 可得到矩阵方程
式中:Ug=[u1u2u3 … un 0 0 … 0]T; a0=[a1a2 … an b1b2 … bm]T。因为矩阵R0是对称的, 故矩阵G也是对称的。求解式(8)可得
将式(4)写为矩阵形式
将式(9)代入式(10)得
式中
相应的导数表达式为
RPIM形函数满足Kronecker delta函数性质, 第一类边界条件加载便利; 然而, RBF中包含了对RPIM计算精度有直接影响的形状参数, 其最优值需要通过数值试验获得。
定义了无网格形函数, 便可以构造式(1)的离散系统方程, 将变分符号代入式(1), 有
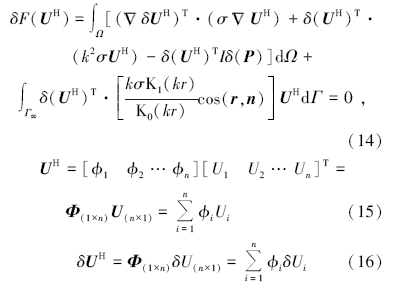
式中:Φ 为形函数矩阵; n为支持域内的节点数; u为支持域内n个节点的场向量。将式(16)、式(15)与式(13)代入式(14), 引入总体编号体系, 式(14)最终变为:
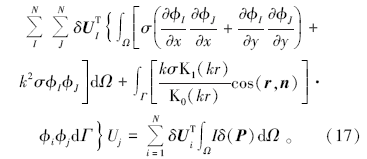
式(17)右端的积分代表点源对二维电场的贡献, δ 函数积分存在式(18)的数值解
式中:x0与y0为点源P所在位置的坐标。将式(18)代入式(17)得
由于δ UT是任意的, 故式(19)成立的条件为
式(20)即为无网格法构造的系统方程。由于求解域为矩形, 具体计算时应先将K包含的无穷边界积分项展开为
式中r=
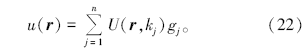
| 表1 最优化波数 |
K的表达式中包含对求解域Ω 与求解域边界Γ 的积分, 为计算这些积分, 一般采用一组背景网格将区域离散(图1), 总体积分表示成离散单元积分之和的形式, 每个单元的积分利用高斯积分法求解:
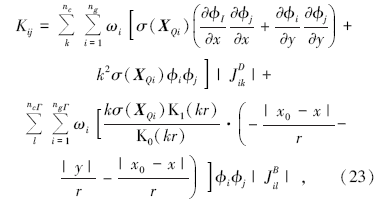
式中:nc与ncΓ 分别为背景单元及边界单元的个数; ng与ngΓ 分别为背景单元及边界单元内的高斯点数目, ω i为第i个高斯点XQi的权系数;
首先通过不含形状参数的EFGM来试验点源二维正演问题支持域无量纲尺寸的最优值, 计算对象为ρ =1 000 Ω · m的均匀介质模型。表2为不同支持域无量纲尺寸的EFGM数值计算结果, 由表2可知, 点源二维正演问题α 最优值为1.0~1.2。由于α 增大的同时增加了计算耗时[13], 故之后的RPIM最优形状参数试验取α =1.0。
| 表2 不同支持域无量纲尺寸EFGM数值计算结果 |
表3~表6列出了基于MQ函数、EXP函数及TPS函数的RPIM在不同形状参数下的计算结果。如表3~表4所示, MQ函数形状参数具有较大的动态范围, α c取值区间约[-6, 6], q取值区间约[-44, 9], 超过此区间, RPIM计算会产生奇异; 最优形状参数α c=1.0, q=-5.8。表5、表6显示EXP函数最优形状参数α c=6.3, TPS函数最优形状参数η =1.43或η =1.6。
| 表3 α c=1.0时不同q值的RPIM(MQ)计算结果 |
| 表4 q=-5.8时不同α c值的RPIM(MQ)计算结果 |
| 表5 RPIM(EXP)不同形状参数计算结果 |
| 表6 RPIM(TPS)不同形状参数计算结果 |
RPIM(MQ)处理点源二维正演问题具有很好的普适性, 其形状参数动态范围最大, RPIM(EXP)次之; 计算精度由高到低依次为RPIM(MQ)→ RPIM(TPS)→ RPIM(EXP)。
表7列出了最优形状参数下不同高斯点数量的RPIM计算结果。由表可见, 高斯点数量的增加对计算精度无明显提升效果, 2~4点高斯积分公式已能满足精度要求。
| 表7 不同高斯点数量RPIM计算结果 |
1) 利用径向基函数近似求解域中的点源二维电位具有边界条件加载便利、精度高的优点。RBF形状参数对RPIM计算精度影响大, 通过数值试验获得了适用于直流点源问题MQ(multi-quadrics)函数、薄板样条(thin plate spline, TPS)函数、高斯指数(EXP)函数形状参数及支持域无量纲尺寸α 的建议值或区间:RPIM(MQ)形状参数建议取α c=1.0, q=-5.8; RPIM(EXP)建议取α c=6.3; RPIM(TPS)建议取η =1.43或η =1.6, 建议α 为1.0~1.2。
2) 对比了最优形状参数推荐值下RPIM模拟点源电阻率参量的精度, 相同高斯积分点RBF近似精度由高至低为MQ、TPS、EXP; 增加背景单元内的高斯点对提高RPIM求解精度作用有限, 反而会降低计算效率, 选用2~4点高斯积分公式即可。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|