基于马蒙算法地质统计学反演的缝洞储集体预测

引用本文

韩东, 胡向阳, 邬兴威, 刘坤岩, 司朝年, 付鑫, 贾志坤. 基于马蒙算法地质统计学反演的缝洞储集体预测[J]. 物探与化探, 2017,39(6): 1211-1216.
HAN Dong, HU Xiang-Yang, WU Xing-Wei, LIU Kun-Yan, SI Chao-Nian, FU Xin, JIA Zhi-Kun. The prediction research on fracture-cavity reservoirs by geostatistical inversion based on Markov Chain and Monte-Carlo algorithm in the Tahe oilfeild[J]. Geophysical and Geochemical Exploration, 2017,39(6): 1211-1216. 复制到剪切板

Doi:10.11720/wtyht.2015.6.19
Permissions

《物探与化探》编辑部

基于马蒙算法地质统计学反演的缝洞储集体预测

韩东¹, 胡向阳¹, 邬兴威¹, 刘坤岩¹, 司朝年¹, 付鑫², 贾志坤³

1.中国石油化工股份有限公司石油勘探开发研究院,北京 100083

2.中国石油集团公司长城钻探测井公司,辽宁盘锦 124010

3.中化石油勘探开发有限公司,北京 100031

作者简介: 韩东(1986-),男,助理工程师,2012年毕业于中国石油大学(北京)油气田开发地质专业并获硕士学位,研究方向为油气田开发地质及储层预测。E-mail:handong.syky@sinopec.com

收稿日期: 2015-03-23

基金: 国家科技重大专项课题“缝洞型碳酸盐岩油藏三维地质建模技术”(2011ZX05014-002)

摘要

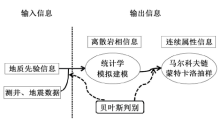
塔河油田缝洞储集体空间非均质性强,基于地震资料的确定性预测方法表征缝洞储集体时存在多解性。采用一种基于马蒙算法的地质统计学反演方法实现了缝洞储集体的定量预测并作出不确定性评价。首先从地质、地球物理角度获取目标区储集体发育的先验信息,再进行地质统计学参数的实验调试,最终利用地质统计学反演获得储集体岩相类型结果及波阻抗结果的多个实现,并对预测结果作出不确定性评价。该方法提供了一种地震数据主导的缝洞储集体定量预测手段,能够较好地解决溶洞储集体纵向深度归位、地震预测成果不确定评价问题,对于该类油藏的地质建模表征具有指导意义。

关键词: 缝洞型油藏; 储集体预测; 马蒙算法; 地质统计学反演; 不确定性评价

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)06-1211-06

The prediction research on fracture-cavity reservoirs by geostatistical inversion based on Markov Chain and Monte-Carlo algorithm in the Tahe oilfeild

HAN Dong¹, HU Xiang-Yang¹, WU Xing-Wei¹, LIU Kun-Yan¹, SI Chao-Nian¹, FU Xin², JIA Zhi-Kun³

1.SINOPEC Exploration&Production Research Institute,Beijing 100083,China;

2.Logging Company of PetroChina Great Wall Drilling Company,Panjin 124010,China

3.Sinochem Petroleum Exploration & Production Co.Ltd,Beijing 100031,China;

Abstract

The spatial heterogeneity of carbonate fractured-vuggy reservoir is very strong in the Tahe oilfeild.Interwell reservoir prediction mainly depends on the application of seismic data.However,the results of deterministic seismic interpretation have multi-solutions.A geostatistical inversion method based on Markov Chain and Monte-Carlo algorithm is adopted for fractured-vuggy reservoir quantitative prediction and uncertainty evaluation.Firstly,geological prior information of the target zone can be obtained by geological regularity and deterministic interpretation results from well logging and seismic survey.Then,controlled by suitable geostatistical simulation parameters of the study area,the geostatistical inversion can be done, yielding many equal probability results of reservoir type volume and impedance data volume.Based on these results,the uncertainty of inversion can be analyzed.The method provides an effective seismic-driven way for quantitative prediction of fractured-vuggy reservoir,giving better solutions to the problems of the cave vertical depth positioning and the uncertainty evaluation of seismic prediction results.It is of great guiding significance for the modeling and characterization of fractured-vuggy reservoir.

Keyword: fractured-vuggy reservoir; quantitative prediction; Markov Chain and Monte-Carlo; geostatistical inversion; uncertainty evaluation

Show Figures

塔河油田中下奥陶地层(以 $\begin{matrix} T_{7}^{4} \end{matrix}$ 区域不整合面为顶界面)为典型的缝洞型油藏, 多种储集体类型共存, 且形态尺度差异大, 空间非均质性强。独立、缺乏连续性是该类储集体非均质性的主要特征。如何有效预测该类油藏储集体展布是制约其开发效果的关键因素。

由于油藏储集体的强分均质性, 传统碎屑岩中常用的“ 相控” 与“ 层控” 地质建模储集体预测方法在该类油藏已不再适用。依赖于地震资料的储层预测已成为该类油藏缝洞型储集体预测与表征的重要手段, 因此前人在塔河地区的缝洞储集体预测方面做了大量的探索工作, 并取得显著效果。王世星、曹鉴华等^{[1, 2]}从能量、波形结构等原始地震属性角度得到的储集体预测成果为现场生产提供了有效支撑。胡向阳、侯加根、刘钰铭^{[3, 4, 5, 6, 7]}等则依靠地质建模技术, 创新性地将地质、地震、测井等多尺度数据整合, 实现了不同缝洞储集体的的单独刻画及物性模拟, 在油藏规模上定量评价了缝洞储集体空间非均质性^[8]。但目前对于缝洞型储集体的预测表征仍存在不少问题, 例如地质建模类预测方法中的多点地质统计学算法并不适用于塔河地区非河道储集体的预测^[9], 而地震响应的放大作用导致的大尺度溶洞储集体的深度归位问题^[10], 以及地震预测成果本身带来的不确定性问题也缺少深入研究。

本次研究利用一种基于马尔科夫链— 蒙特卡洛算法(MCMC)的地质统计学反演方法(以下简称MC地质统计学反演), 实现了塔河油田某区缝洞储集体的定量预测。该方法融入了对于储集体发育规律的地质认识, 并融合不同尺度数据, 获得多个反映目标区缝洞储集体发育规律的等概率实现结果^[11]。由于反演本身以反映地震信息为主, 在多次反演结果的基础上可对储集体预测结果的不确定性进行评价, 这为缝洞储集体的定量预测提供了一种切实可行的方法。

1 MC地质统计学反演基本原理

地震反演技术, 简单而言可认为是将常规地震资料的界面型反射剖面转化为岩性地层剖面的过程。反演最终结果是反映岩石弹性信息的波阻抗数据体。MC地质统计学反演则是在常规地震反演技术的基础上, 加入地质、测井、物探等反映储集体发育规律的先验信息, 再以统计学方法为手段, 通过反演算法的耦合, 获得同时满足地震数据与输入先验信息的一种地震储集体预测方法。其本质上属于反演而非“ 模拟” , 是一种地震约束的油藏属性建模方法, 因此更加忠实于地震数据, 反演结果在提供更高垂向分辨率的同时, 井间充分利用地震数据的横向信息, 目前多用于油藏开发中后期的储集体表征工作中。由于地质统计学反演方法在纵向上有更高的分辨率, 缝洞储集体预测结果将更好地匹配于钻井资料解释结论, 这也为研究区发育较大尺度的溶洞储集体纵向归位奠定理论基础。

MC地质统计学反演的核心是贝叶斯判别理论与马尔科夫链蒙特卡洛抽样算法。贝叶斯判别理论能够根据输入数据(地震、测井)与先验信息, 综合其概率密度函数得到储集体发育的后验概率分布函数, 即获得多种概率的空间交集(可理解为所求取的储集体空间发育规律)。从理论上讲, 贝叶斯推断和分析是比较容易实施的, 因为其本质上就是计算后验分布某一函数的高维积分。但是由于最终反演结果的求解是多维度的, 贝叶斯推断所获得的后验分布函数的求解就变得异常复杂。

马尔科夫链蒙特卡洛算法(MCMC)则能够解决针对后验概率分布函数的求解问题, 它通过模拟的方式对高维积分进行计算, 进而使原本异常复杂的高维积分问题迎刃而解^[12]。该方法属于启发式反演算法, 其基本思想是通过重复抽样, 建议一个平稳分布为所求后验分布的马尔科夫链, 得到后验分布的样本, 基于这些样本再作各种统计推断^[13]。算法本身仍属于蒙特卡洛方法, 其基础是对概率分布的直接模拟。设ϕ 为某一空间, n为产生的总样本数, m为链条达到平稳时的样本数, 则MCMC的基本思路可以概括为^[12]

1)构造Markov链:构造一条Markov链, 使其收敛到平稳分布π (x);

2)产生样本:由ϕ 中的某一点x⁽⁰⁾出发, 用(1)中的Markov链进行抽样模拟, 产生点序列:x⁽¹⁾, x⁽²⁾, …, x⁽ⁿ⁾;

3)蒙特卡洛积分。任一函数f(x)的期望估计

$\begin{matrix} E [f (x)] = \frac{1}{n - m} \overset{n}{\sum_{t = m + 1}} f (x^{(t)}) 。 \end{matrix}$

通过该算法抽样之后, MC地质统计学反演便将传统地质统计学建模与确定性地震反演技术结合起来, 综合地质、地震、测井等信息, 获得高于常规地震反演分辨率的储集体预测结果^[14]。由于在反演时直接由原始地震数据参与, 而不需以确定性反演结果作为输入条件, 因此结果更加尊重原始地震数据, 受人为影响减小。

	Figure Option View Download New Window
	图1 MC地质统计学反演基本原理

2 MC地质统计学反演实现流程

2.1 地质资料(先验信息)分析

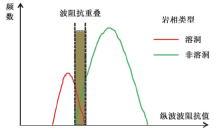
先验信息包括的种类较多, 前期的地质认识、地震解释获得的地层格架、测井分析得到的岩石物理模型及地质统计学参数, 都可以作为先验信息来约束反演结果。从井点解释成果来看, 缝洞型油藏的储集体发育主要包括三种类型:溶洞型、溶蚀孔洞型、裂缝型。其中溶洞型储集体在声波时差曲线上的差异较明显, 表现为典型的高值(对应于波阻抗值则为低值), 溶蚀孔洞型与裂缝型较非储集体声波时差有异常, 但幅度较小(波阻抗值较低), 与碳酸盐岩基质较难区分。因此, 准备先验信息时, 需将溶蚀孔洞与裂缝型储集体以及碳酸盐岩基质合并为一类储集体类型, 即非溶洞相类型。虽然溶洞与非溶洞相在波阻抗上仍有部分叠置(图2), 但叠置部分结果的多解性将在后续不确定性评价中得到体现。

	Figure Option View Download New Window
	图2 纵波阻抗对缝洞储集体的区分度示意

2.2 地质统计学模拟参数调试

地质统计学模拟参数测试是对前面地质资料分析得到的认识进行定量化设置, 并测试其合理性, 最终确定的参数与地震解释层位一样将作为先验信息用于后续地质统计学反演的过程约束^[15]。需要测试的参数包括离散岩相信息与连续属性信息两部分。对于离散岩性信息, 需要测试不同岩相类型发育比例、变差函数。对于连续属性信息, 需要测试不同岩相类型的连续属性(例如波阻抗属性)的概率分布函数和变差函数。具体测试参数如表1所示。

表1 地质统计学模拟参数调试分类

对于离散岩相数据, 岩性发育比例参数是根据井点解释结论统计获得或者基于对研究区沉积背景的地质认识进行设置。对于连续属性数据, 主要分析对应储集体类型在该属性上的概率分布函数, 一般需要转换为高斯分布, 方便后续模拟过程的采样。变差函数作为控制离散岩相和连续属性纵向以及平面展布范围的参数, 则需单独调试。

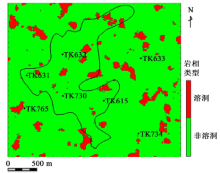
图3是根据确定后地质统计学参数模拟产生的岩相类型切片。由于地质统计学模拟产生的结果是在没有地震参与情况下获得的, 其反映出的溶洞储集体展布模式与前期地质认识相符(除少数河流成因溶洞外, 溶洞分布多呈离散状, 平面连续性差), 说明设置参数是合适的。需要说明的是, 这里的模拟参数在反演过程中只起到一个软约束的作用, 但能够保证最终反演结果在储集体展布上的合理性^[16]。

	Figure Option View Download New Window
	图3 地质统计学模拟得到的岩相数据体切片(奥陶系不整合面 $\begin{matrix} T_{7}^{4} \end{matrix}$ 以下20 ms)

2.3 MC地质统计学反演

在确定地质统计学模拟参数之后, 加入提取的地震子波, 以及地震数据, 即可进行MC地质统计学反演工作。在反演时可以通过地震信噪比参数控制地震数据对最终反演结果的贡献程度。信噪比参数是描述地震数据体噪声相对值的物理量, 可以参考井震标定以及常规约束稀疏脉冲反演方法获得的地震数据的信噪比信息来进行参数设置。由于反演过程中通过地质统计学参数加入了测井成果以及地质分析获得的先验信息, 因此反演结果分辨率得到很大提高。

3 实例分析

3.1 缝洞储集体预测结果

通过对塔河油田某区的地质资料分析, 确定了不同类型岩相发育比例及地质统计学参数。通过MC地质统计学反演获得多个等概率的反演实现。图4是得到的一个实现结果, 分别是反演得到的波阻抗及岩相结果。可以看出二者本身具有较好的吻合性:波阻抗值低的部分主要为尺度较大、物性较好的溶洞型储集体; 而对于非溶洞储集体部分, 波阻抗值的差异则反映出物性存在差异, 即波阻抗值较高的部分为孔洞— 裂缝型储集体, 波阻抗值最高的部分则为致密碳酸盐岩基质。但是这种对应关系并不是确定的, 原因有两个方面:一是反演过程中加入了地质统计先验信息, 结果中的高频信息包含一定的随机性。二是反演的岩相类型存在波阻抗值域上的叠置, 因此对于中间值域的波阻抗在反映岩性信息时也具有不确定性。

	Figure Option View Download New Window
	图4 MC地质统计学反演得到的波阻抗数据体(上)与岩相数据体连井剖面(下)

由于反演所获得的溶洞储集体厚度明显低于地震可识别厚度, 所以预测溶洞的纵向归位是否准确仍需验证。对此, 可制作简化的溶洞发育模型通过正演手段来进行对比说明。图5所示为模拟 $\begin{matrix} T_{7}^{4} \end{matrix}$ 不整合面以下不同深度段的溶洞模型正演所获得的地震响应波形。由于研究区地震可识别溶洞储集体规模多在5~15 m, 远远小于地震波长的四分之一(约50 m), 地震反射波形难以区分溶洞顶底界, 且溶洞顶底反射波形相干涉, 使得溶洞主要落在波谷— 波峰零相位处。但当溶洞距离不整合面距离较近时, 溶洞反射将与不整合面反射相叠加, 致使不整合面处振幅能量减弱, 或产生复波。对比反演波阻抗剖面:溶洞发育段(波阻抗低值处)主要对应于地震反射波谷至波峰反射的零相位以及不整合面附近复波处, 这与溶洞模型正演结果相一致, 说明反演结果对于溶洞型储集体的纵向归位是相对可靠的。

	Figure Option View Download New Window
	图5 距离不整合面不同深度溶洞的正演响应

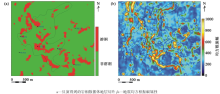
同时, 反演岩相结果与地质统计学模拟岩相结果的差异将体现地震数据在反演运算中所起的作用。从反演得到的岩相数据体地层切片来看(图6a), 预测溶洞范围与地震均方根振幅属性(图6b)显示的地震强能量反射位置相一致, 反映出研究区类“ 串珠状” 反射为溶洞储集体发育优势区带。且溶洞储集体在北西— 南东向呈条带状展布, 结合塔河地区岩溶发育模式^{[17, 18, 19, 20]}认为该深度段为古岩溶水平潜流带的地下暗河沉积发育, 因此连通性较好。从T615井钻井取芯来看, 暗河沉积溶洞存在异地砂泥质沉积物充填现象, 因此产能会受此影响。除暗河沉积溶洞外, 孤立离散状分布也是该区溶洞发育的显著特点。

	Figure Option View Download New Window
	图6 地质统计学反演岩相数据体切片(奥陶系不整合面 $\begin{matrix} T_{7}^{4} \end{matrix}$ 以下20 ms)

由于声波速度主控的波阻抗参数在一定程度上反映了储集体的综合物性信息^[21], 可根据波阻抗与孔隙度的协同关系, 将波阻抗数据体转换为反映缝洞储集体等效孔隙度数据体, 在此基础上可对研究区物性作出定量评价。

3.2 结果不确定性评价

MC地质统计学反演的中低频信息来源于地震资料, 高频信息来源于测井资料以及地质分析获得的先验信息, 因此最终反演结果具有统计学上的不确定性。同时溶洞与非溶洞岩相类型在波阻抗值域上的部分叠置, 也使得相同波阻抗值对应的储集体类型并不唯一。这也是在追求储集体预测高分辨率与高精度效果时必须面临的问题。尤其是对于缝洞型这类对地震预测成果依赖性很强的油藏类型来说, 地震资料及预测成果的不确定评价尤其重要。

地质统计学理论的优势便在于可以对预测成果进行多次等概率实现。结合研究区MC地质统计学反演的多次实现结果, 利用概率分析工具得到了溶洞储集体发育概率体以及岩相极大似然体, 如图7所示。概率体代表多次实现中同一储集体出现的概率, 极大似然体则代表统计学上储集体最可能出现的情况。从评价结果来看, 溶洞发育主要集中在强波谷— 强波峰转换的零相位处, 另外在地震反射能量较强— 中等的部位, 仍有溶洞发育的可能性, 但溶洞规模相比强反射区要小, 利用地震资料刻画的难度加大。

	Figure Option View Download New Window
	图7 MC地质统计学反演结果的储集体概率发育体剖面(上)及极大似然体剖面(下)

通过不确定性评价分析, 将储集体预测结果以概率体的形式进行应用, 能够弥补确定性反演结果对于地震解释结果多解性的掩盖, 对缝洞储集体的地质表征研究具有更科学的指导意义。

4 结论

1)MC地质统计学反演是一种将地震反演与地质建模技术相结合的新型反演方法, 通过贝叶斯判别理论与马尔科夫链蒙特卡洛抽样算法实现了地震数据驱动下的精细波阻抗反演, 在提高纵向储集体分辨能力的同时能够得到溶洞储集体纵向发育的相对位置, 同时为缝洞储集体的物性评价提供约束条件。

2)反演结果的多次实现可为缝洞储集体地震预测成果的多解性提供一种有效分析手段。通过对反演多次实现结果进行不确定性分析, 得到缝洞储集体发育的概率体, 实现地震预测结果不确定性的定量评价, 更好地用于后期缝洞型油藏地质建模表征研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王世星, 曹辉兰, 靳文芳, 等. 碳酸盐岩缝洞系统地震响应特征分析和塔中卡1区缝洞储层预测[J]. 石油物探, 2005, 44(5): 421-427. [本文引用:1]
[2]	曹鉴华, 张学丰. YQ地区奥陶系碳酸盐岩岩溶储层地震属性预测[J]. 特种油气藏, 2012, 19(2): 42-45. [本文引用:1]
[3]	胡向阳, 李阳, 权莲顺, 等. 碳酸盐岩缝洞型油藏三维地质建模方法——以塔河油田四区奥陶系油藏为例[J]. 石油与天然气地质, 2013, 34(3): 383-387. [本文引用:1]
[4]	胡向阳, 权莲顺, 侯加根. 岩溶相控多尺度碳酸盐岩缝洞储集体二步法建模新技术[J]. 科技导报, 2013, 31(24): 42-46. [本文引用:1]
[5]	侯加根, 马晓强, 刘钰铭, 等. 缝洞型碳酸盐岩储层多类多尺度建模方法研究: 以塔河油田四区奥陶系油藏为例[J]. 地学前缘, 2012, 19(2): 59-66. [本文引用:1]
[6]	刘钰铭, 侯加根, 胡向阳, 等. 塔河油田古岩溶储集体三维建模[J]. 中国石油大学学报: 自然科学版, 2012, 36(2): 34-38. [本文引用:1]
[7]	胡向阳, 李阳, 王友启, 等. 三维地质模型概率法在碳酸盐岩缝洞型油藏石油地质储量研究中的应用——以塔河油田四区为例[J]. 油气地质与采收率, 2013, 20(4): 46-48. [本文引用:1]
[8]	杨锴, 艾迪飞, 耿建华. 测井、井间地震与地面地震数据联合约束下的地质统计学随机建模方法研究[J]. 地球物理学报, 2012, 55(8): 2695-2704. [本文引用:1]
[9]	石书缘, 尹艳树, 冯文杰. 多点地质统计学建模的发展趋势[J]. 物探与化探, 2012, 36(4): 655-660. [本文引用:1]
[10]	李胜军, 刘伟方, 高建虎. 正演模拟技术在碳酸盐岩溶洞响应特征研究中的应用[J]. 岩性油气藏, 2011, 23(4): 106-109. [本文引用:1]
[11]	王家华, 王镜惠, 梅明华. 地质统计学反演的应用研究[J]. 吐哈油气, 2011, 16(3): 201-204. [本文引用:1]
[12]	朱新玲. 马尔科夫链蒙特卡罗方法研究综述[J]. 统计与决策, 2009, 297(21): 151-153. [本文引用:2]
[13]	张广智, 王丹阳, 印兴耀. 利用MCMC方法估算地震参数[J]. 石油地球物理勘探, 2011, 46(4): 605-609. [本文引用:1]
[14]	何火华, 李少华, 杜家元, 等. 利用地质统计学反演进行薄砂体储层预测[J]. 物探与化探, 2011, 35(6): 804-808. [本文引用:1]
[15]	姜文龙, 杨锴. 岩石物理参数高分辨率地质统计学反演[J]. 石油物探, 2012, 51(6): 638-648. [本文引用:1]
[16]	董奇, 卢双舫, 张学娟, 等. 地质统计学反演参数选取及反演结果可靠性分析[J]. 物探与化探, 2013, 37(2): 328-332. [本文引用:1]
[17]	牛玉静, 康志宏, 龙旭, 等. 塔河油田奥陶系岩溶油藏溶洞储集体成因及演化[J]. 现代地质, 2011, 25(4): 650-659. [本文引用:1]
[18]	漆立新, 云露. 塔河油田奥陶系碳酸盐岩岩溶发育特征与主控因素[J]. 石油与天然气地质, 2010, 31(1): 1-12. [本文引用:1]
[19]	鲁新便, 高博禹, 陈姝媚. 塔河油田下奥陶统碳酸盐岩古岩溶储层研究——以塔河油田6区为例[J]. 矿物岩石, 2003, 23(1): 87-92. [本文引用:1]
[20]	周江羽, 吕海涛, 林忠民, 等. 塔河油田奥陶系岩溶作用模式及控制因素[J]. 石油实验地质, 2009, 31(6): 547-550. [本文引用:1]
[21]	陈继华, 肖亮, 毛志强. 溶孔洞型含气碳酸盐岩储层孔隙度评价方法研究[J]. 石油天然气学报, 2011, 33(6): 92-97. [本文引用:1]

2005

0.0

... 王世星、曹鉴华等^[1,2]从能量、波形结构等原始地震属性角度得到的储集体预测成果为现场生产提供了有效支撑 ...

2012

0.0

... 王世星、曹鉴华等^[1,2]从能量、波形结构等原始地震属性角度得到的储集体预测成果为现场生产提供了有效支撑 ...

2013

0.0

胡向阳, 李阳, 权莲顺, 等. 碳酸盐岩缝洞型油藏三维地质建模方法——以塔河油田四区奥陶系油藏为例[J]. 石油与天然气地质, 2013, 34(3): 383-387.

Reservoir spaces of fractured-vuggy carbonates mainly,include large caverns,dissolved pores and fractures,which are varied in scale,irregular in shapes and discontinuous in distribution.There still have no effective geological modeling method for quantitative descriptions of 3D reservoir space distributions in fractured-vuggy carbonate reservoirs.In this paper,taking Tahe fractured-vuggy carbonate reservoir as an example,we put forward a 3D geological modeling method of fractured-vuggy reservoir under the constraint of multiple geological factors,i.e.two-step modeling under the control of ancient karst development pattern.In the first step,4 single-type reservoir models were established.After large cavens and large-scale fractures were identified by using seismic data,a discrete large cavern model and a discrete large-scale fracture model were established first with deterministic modeling method.Then,under the constraint of karst facies and based on development probability volumes of dissolved pores and interwell fractures,a dissolved pore model and a discrete small-scale fracture model were established by using the stochastic multi-attribute coordinated modeling method.In the second step,the 4 single-type reservoir models were merged into a 3D multiscale discrete geological model of fractured-vuggy carbonate reservoirs by using the diadochic assignment algorithm.The final model can quantitatively describe the 3D distribution of the fractured-vuggy carbonate reservoirs,and provide geological foundation for oilfield development.

1. Exploration & Production Research Institute, SINOPEC, Beijing 100083, China; 2. Exploration and Production Department, SINOPEC, Beijing 100728, China

碳酸盐岩缝洞型油藏储集空间类型主要为大型溶洞、溶蚀孔洞及裂缝,尺度大小悬殊,形态不规则,分布不连续。定量刻画孔、洞、缝在三维空间的展布一直是该类油藏开发的技术难题,目前尚缺乏有效的地质建模方法。以塔河碳酸盐岩缝洞型油藏为原型,提出了多元约束碳酸盐岩缝洞型油藏三维地质建模方法,即在古岩溶发育模式控制下,采用两步法建模。第一步,建立4个单一类型储集体模型:首先利用地震识别的大型溶洞和大尺度裂缝,通过确定性建模方法,建立离散大型溶洞模型和离散大尺度裂缝模型;然后在岩溶相控约束下,基于溶洞发育概率体和井间裂缝发育概率体,采用随机建模多属性协同模拟方法,建立溶蚀孔洞模型和小尺度离散裂缝模型。第二步,采用同位条件赋值算法,将4个单一类型模型融合成多尺度离散缝洞储集体三维地质模型。该模型定量刻画了缝洞储集体在三维空间的展布特征,为油田开发奠定了坚实的地质基础。

... 胡向阳、侯加根、刘钰铭^[3,4,5,6,7]等则依靠地质建模技术,创新性地将地质、地震、测井等多尺度数据整合,实现了不同缝洞储集体的的单独刻画及物性模拟,在油藏规模上定量评价了缝洞储集体空间非均质性^[8] ...

2013

0.0

胡向阳, 权莲顺, 侯加根. 岩溶相控多尺度碳酸盐岩缝洞储集体二步法建模新技术[J]. 科技导报, 2013, 31(24): 42-46.

Taking Tahe fractured-cavity carbonate reservoirs as the prototype,a new technology of the two step modeling controlled by karst facies of multi-scale fractured-cavity reservoir is developed. It is a two step modeling method under the control of the ancient karst development mode: the first step is the establishment of four discrete distribution models of a single type of reservoir, namely, using the seismic identification and description of the results, to establish a large cave discrete distribution model and a large-scale fracture discrete distribution model. With the karst facies constraints, based on the probability of caves and fractures to be developed between the body and the wells, and the multi-attribute co-simulation, the dissolved pores stochastic model and the small scale fractures discrete model are built. In the second step the parity condition assignment algorithm is used, to integrate the four single types of models into a multi-scale discrete fractured-cavity reservoir 3D distribution model. The quantitative model in 3D space to characterize the distribution feature of the fractured-cavity reservoir may serve as a solid geological foundation for the oilfield development.

1. SINOPEC Exploration and Production Research Institute, Beijing 100083,China;2. College of Geoscience, China University of Petroleum(Beijing), Beijing 102249, China

以塔河碳酸盐岩缝洞型油藏为原型,研究并形成了岩溶相控多尺度缝洞储集体二步法建模新技术,即在古岩溶发育模式控制下,采用二步法建模:第1步建立4个单一类型储集体离散分布模型,利用地震识别的大型溶洞和大尺度裂缝,通过确定性建模方法,建立离散大型溶洞模型和离散大尺度裂缝模型;在岩溶相控约束下,基于溶洞发育概率体和井间裂缝发育概率体,采用随机模拟多属性协同模拟方法,建立溶蚀孔洞模型和小尺度离散裂缝模型;第2步采用同位条件赋值算法,将4个单一类型模型融合成多尺度离散缝洞储集体三维分布模型。该模型在三维空间定量表征了缝洞储集体的展布特征,为油田开发奠定了坚实的地质基础。

2012

0.0

2012

0.0

2013

0.0

2012

0.0

杨锴, 艾迪飞, 耿建华. 测井、井间地震与地面地震数据联合约束下的地质统计学随机建模方法研究[J]. 地球物理学报, 2012, 55(8): 2695-2704.

Based on a geostatistical simulation method conditioned to well-log and crosshole seismic rays, a novel geostatistical reservoir inversion (modeling) technique constrained by well-og, crosshole and surface seismic data is presented. Compared with existing geostatistical inversion methods only the well-log and surface seismic data being honored, all related prior infomation include well-log, crosshole seismic data and surface seimismic data are honored in presented method. Thus the accuracy of geostatistical inversion/modeling is greatly improved and the uncertainty of inversion/modeling is reduced. The test on synthetic data proved the above points.

[Yang Kai; Ai Di-Fei; Geng Jian-Hua] Tongji Univ, State Key Lab Marine Geol, Shanghai 200092, Peoples R China.

利用能够整合测井信息与井间地震信息的地质统计学随机模拟方法,结合传统的地质统计学反演思路,得到了一种能够同时整合测井、井间地震与地面地震三种先验信息的地质统计学反演与储层建模方法.由于井间射线信息、测井信息与地面地震数据在随机反演与建模过程当中都得到了尊重,因此与传统地质统计学反演仅利用了测井与地面地震数据相比,本文的地质统计学反演与建模方法更充分地利用了先验信息,有效提高了反演的精度,降低了随机建模中的多解性.基于理论数据的测试证实了上述观点.

2012

0.0

石书缘, 尹艳树, 冯文杰. 多点地质统计学建模的发展趋势[J]. 物探与化探, 2012, 36(4): 655-660.

Starting with algorithm designing, training image,and practical application,the authors analyzed multiple-point statistics research trends both in China and abroad.On such a basis,the core principles of the main four MPS algorithms,their applicable ranges and advantages as well as disadvantages were analyzed,so as to forecast the trend of reservoir modeling.Multiple-point geostatistics is an international forefront research tool in stochastic modeling;nevertheless,as the algorithm is not yet mature,it should be further improved.On the basis of previous researches,the existing problems of the multiple-point geostatistics that need to be modified and the direction of the processing of training images are proposed,such as suitable processing of training image,choice of similarity methods,choice of standardized data,smoothing,coupling among algorithms,and expansion of the simulation extent for fractured-vuggy carbonate reservoir.In order to improve the usage of multiple-point geostatistics for reservoir stochastic modeling,we should spare no efforts to increase the simulation area,improve simulation accuracy,expand the scope of simulation of reservoir types,save simulation time and improve simulation efficiency.

1. Research Institute of China Petroleum Exploration & Development, PetroChina, Beijing 100083, China; 2. School of Geosciences, Yangtze University, Jingzhou 434023, China; 3. China University of Petroleum, Beijing 102249, China

从算法研究、训练图像处理和实际应用三个方面详细解剖了国内外多点地质统计学的发展历程,在此基础上,分析了多点地质统计学主流的几种算法的核心原理、适用范围及优缺点,以此来对储层建模的发展趋势作出展望。目前,多点地质统计学虽是随机建模的一种前沿研究热点,但由于其尚未成熟,仍需对建模算法进行研究。为此,在前人研究的基础上,重点分析了多点地质统计学的发展趋势:合理处理训练图像;合理利用软信息;选择合适的相似性方法;选择合适的标准化方法;合理利用平稳性;算法间的耦合;选择合适的过滤器;拓展缝洞型碳酸盐岩模拟。最后,提出多点地质统计学在储层建模方面,应从增加储层的模拟区域、提高模拟精度、扩大储层相的模拟范围和提高计算机模拟效率等方面进行改进。

... 但目前对于缝洞型储集体的预测表征仍存在不少问题,例如地质建模类预测方法中的多点地质统计学算法并不适用于塔河地区非河道储集体的预测^[9],而地震响应的放大作用导致的大尺度溶洞储集体的深度归位问题^[10],以及地震预测成果本身带来的不确定性问题也缺少深入研究 ...

2011

0.0

李胜军, 刘伟方, 高建虎. 正演模拟技术在碳酸盐岩溶洞响应特征研究中的应用[J]. 岩性油气藏, 2011, 23(4): 106-109.

The “string bead” reflection is one of the important seismic response features in identification ofOrdovician carbonation reservoir in TarimBasin. The mechanismof “string beads” is very complex. Base on forward modeling ofwave equation, some different models are designed, and the influence of cave width and height on “string bead” characteristics is analyzed. The result shows that the amplitude of “string bead” intensifies with the cave width increasing, but the length of “string bead” do not change. The amplitude of “string bead” firstly intensifies and then decreases with the cave height increasing , and the“string bead” lengthens. Forward modeling provides approach for further study of response mechanismof cave, cave shape and “string bead” features, and criterion for semi-quantitative and quantitative forecast of carbonate reservoir.

Research Institute of Petroleum Exploration & Development-Northwest， PetroChina， Lanzhou 730020， China

在塔里木盆地奥陶系碳酸盐岩储层识别中，“串珠状”反射是十分重要的地震响应特征之一。文中利用波动方程正演模拟技术，设计了不同的溶洞模型，分析了溶洞宽度和高度变化时对“串珠状”响应特征的影响。结果表明：溶洞宽度增加时，“串珠”响应振幅增强，但响应时间长度不变；溶洞高度增加时，“串珠”振幅呈先增大后减小的趋势，且响应时间长度变长。模型正演为进一步研究溶洞的响应机理、溶洞形状与“串珠”特征的关系提供了手段，从而为碳酸盐岩储层的半定量或定量预测提供了依据。

2011

0.0

... 该方法融入了对于储集体发育规律的地质认识,并融合不同尺度数据,获得多个反映目标区缝洞储集体发育规律的等概率实现结果^[11] ...

2009

0.0

... 马尔科夫链蒙特卡洛算法(MCMC)则能够解决针对后验概率分布函数的求解问题,它通过模拟的方式对高维积分进行计算,进而使原本异常复杂的高维积分问题迎刃而解^[12] ...

... 为某一空间,n为产生的总样本数,m为链条达到平稳时的样本数,则MCMC的基本思路可以概括为^[12] ...

2011

0.0

张广智, 王丹阳, 印兴耀. 利用MCMC方法估算地震参数[J]. 石油地球物理勘探, 2011, 46(4): 605-609.

本文介绍了用MCMC（马尔可夫链蒙特卡洛）方法估计地震参数的基本原理及应用。首先利用MCMC方法生成马尔可夫链，然后对链进行统计分析，得到未知参数的估计值。在运用Metropolis-Hastings算法生成马尔可夫链时，可随着迭代次数的增加逐渐减小其游走的步长，以确保迭代初期较早收敛到真值附近，迭代后期在真值附近能得到精度较高的估计值。模型试算结果表明：反演结果与理论模型基本吻合，实际资料的应用效果也证明了算法的有效性。

... 该方法属于启发式反演算法,其基本思想是通过重复抽样,建议一个平稳分布为所求后验分布的马尔科夫链,得到后验分布的样本,基于这些样本再作各种统计推断^[13] ...

2011

0.0

何火华, 李少华, 杜家元, 等. 利用地质统计学反演进行薄砂体储层预测[J]. 物探与化探, 2011, 35(6): 804-808.

The delta-front of a certain area is characterized by fast facies change, strong heterogeneity, and small thickness of a single sand body. As the earthquake-band of the conventional deterministic inversion is limited, the vertical resolution of the seismic inversion body is very low, and hence it is often difficult to identify the small sand body. The geostatistic inversion method based on stochastic modeling technique can effectively integrate geological, logging and seismic data, greatly improve the seismic vertical resolution, and more accurately describe the subtle changes in the reservoir, thus well identifying the thin sand. Geostatistic Inversion was used in delta-front of a target area to predict the thin sand layers. The impedance body derived from the high-resolution geostatistic inversion method was compared with the density body, which could effectively identify a thin layer of sand body in the horizontal distribution on the inversion profile. This method provides a basis for identifying favorable oil and gas traps.

1. MOE Key Laboratory of Oil & Gas Resources and Exploration Technique, Yangtze University, Jingzhou 434023,China; 2. The Zhiluo Oil Production Plant of Yanchang Oil Field Co., Ltd.,Yanan 727500,China; 3. The Shenzhen Branch Institute, CNOOC, Guangzhou 510240,China

某地区三角洲前缘砂体相变快,非均质性强,单砂体厚度小,常规的确定性反演由于受到地震频带限制,反演地震体的垂向分辨力低,往往难以识别。基于随机建模技术的地质统计学反演方法,能有效地综合地质、测井和三维地震数据,极大地提高了预测结果的垂向分辨率,能更加精确地描述储层细微的变化,可以更好地识别薄层砂体。利用地质统计学反演方法对某地区三角洲前缘目标层段的薄层砂体进行了预测,通过高分辨率的地质统计学反演波阻抗体和密度反演体剖面对比,可以有效识别出薄层砂体在反演剖面上横向展布。

... 通过该算法抽样之后,MC地质统计学反演便将传统地质统计学建模与确定性地震反演技术结合起来,综合地质、地震、测井等信息,获得高于常规地震反演分辨率的储集体预测结果^[14] ...

2012

0.0

... 2 地质统计学模拟参数调试地质统计学模拟参数测试是对前面地质资料分析得到的认识进行定量化设置,并测试其合理性,最终确定的参数与地震解释层位一样将作为先验信息用于后续地质统计学反演的过程约束^[15] ...

2013

0.0

董奇, 卢双舫, 张学娟, 等. 地质统计学反演参数选取及反演结果可靠性分析[J]. 物探与化探, 2013, 37(2): 328-332.

Geo-statistical inversion method based on stochastic modeling techniques has high vertical resolution prediction results,but its results show high randomness.Therefore,reliability evaluation of the inversion results is very important.By using geo-statistics method and through setting up different inversion parameters,the authors compared the inversion results and,in combination with geological regularity,selected the optimal inversion parameters to predict thin bedded alternation sand body of SⅡ and SⅢ reservoir group in the development zone of northern Saertu oil field and analyzed the reliability of the inversion results qualitatively and quantitatively based on forward modeling.The results show that rational sampling rate of initial framework,reasonable well density of inversion,and variogram parameters in accord with geological conditions constitute necessary conditions for efficient inversion work and reliable inversion results.

1. College of Geosciences, Northeast Petroleum University, Daqing 163318, China; 2. Provincial Key Lab of Petroleum Accumulation Mechanism and Resource Prediction, Daqing 163318, China

基于随机建模技术的地质统计学反演方法预测结果垂向分辨率高,可细微地刻画储层空间分布,但反演结果随机性较强,因此反演结果的可靠性评价十分重要。笔者利用地质统计学方法,通过设置不同反演参数,对比反演结果,并结合地质规律选取最优反演参数,预测萨北开发区SⅡ和SⅢ油层组薄砂体,以正演模拟为依据,定性和定量分析反演结果的可靠性。结果表明:合理的初始框架采样率和反演井网密度、符合地质条件的变差函数参数,是反演工作高效率和反演结果可靠性高的必要条件。

... 需要说明的是,这里的模拟参数在反演过程中只起到一个软约束的作用,但能够保证最终反演结果在储集体展布上的合理性^[16] ...

2011

0.0

牛玉静, 康志宏, 龙旭, 等. 塔河油田奥陶系岩溶油藏溶洞储集体成因及演化[J]. 现代地质, 2011, 25(4): 650-659.

Karst caves, holes and cracks are important oil conductivity to Ordovician fractured reservoir and control the distribution of oil and gas in Tahe oilfield. Karst system of Ordovician reservoir in Tahe oilfield developed from Caledonian to Early Hercynian. Based on the karst origin,evolution and growth mechanism of Tahe oilfield, it is considered that the north area of pinch O3s is the result of karst in Caledonian and Early Hercynian, and the south area of pinch O3s is the result of karst in Caledonian. Utilization of core, drilling, logging and seismic data, the carbonated caved fracture reservoir caves are divided into 4 types: Excavation or dissolution by aggressive fluids; Deposition of allochthonous （externally derived） sediments; Deposition of autochthonous （internal derivation and precipitation） sediments; Collapse at nearsurface and in subsurface. Finally, the article establishes the distribution pattern of carbonated cavedfracture reservoir.

School of Energy Resources, China University of Geosciences, Beijing 100083, China

古岩溶作用形成的溶洞、溶孔、裂缝构成了塔河油田奥陶系缝洞型油藏的重要储集体，控制油气分布。塔河油田奥陶系古岩溶发育主要经历了加里东期和海西早期岩溶作用的改造，通过对塔河油田岩溶作用演化及发育期次的研究，认为O3s尖灭线以北为海西早期岩溶及加里东期岩溶共同作用的结果，以南区域主要为加里东期岩溶发育区。利用岩心、钻井、录井、测井、地震等资料相结合的方法，将塔河油田溶洞储集体从成因上划分为侵蚀型溶洞、异地沉积物充填型、原地沉积物充填型、塌陷型溶洞4种类型。结合塔河油田岩溶储层发育特征，建立了塔河油田奥陶系岩溶洞穴型储层的纵向分布模式和平面分布模式。

... 南东向呈条带状展布,结合塔河地区岩溶发育模式^{[17,18,19,20]}认为该深度段为古岩溶水平潜流带的地下暗河沉积发育,因此连通性较好 ...

2010

0.0

漆立新, 云露. 塔河油田奥陶系碳酸盐岩岩溶发育特征与主控因素[J]. 石油与天然气地质, 2010, 31(1): 1-12.

The Middle and Lower Ordovician fractured-vuggy reservoirs in the Tahe oilfield experienced multi-stage karstification caused by multi-stage tectonic events from the Middle Caledonian to the Early Hercynian.Based on integration of geological,geophysical and geochemical data,we discuss the development characteristics and main controlling factors of multi-stage karstification of the Ordovician carbonates in the Tahe oilfield.Four main periods of karstification are identified as follows:the 1 st Phase,2 nd Phase and 3 rd Phase of the Middle Caledonian and the Early Hercynian.The origin,evolution and transformation history of the karst reservoirs are also discussed in this paper.According to this study,the major karstification periods are the Early Hercynian,the 1 st Phase and the 2 nd Phase of the Middle Caledonian,of which the Early Hercynian is the most important period.The main controlling factors of kastification are paleostructures,karst topography and geological conditions of paleo-drainage-system.

Petroleum Exploration & Exploitation Research Institute, SINOPEC Northwest Company, Urumqi, Xinjiang 830011, China

塔河油田中-下奥陶统缝洞型储层是加里东中期—海西早期多次构造运动引起的多期岩溶作用叠加改造的结果。结合地质、地球物理和地球化学等分析方法,论述了塔河油田奥陶系碳酸盐岩多期岩溶发育特征及其主控因素,揭示了加里东中期第一幕、第二幕、第三幕和海西早期4个主要岩溶发育阶段,解析了岩溶储层成因演化过程及改造历史,研究认为海西早期及加里东中期第一、第二幕为主要岩溶时期,特别是海西早期最为重要,岩溶发育的主控因素是古构造、岩溶地貌及古水系地质环境。

... 南东向呈条带状展布,结合塔河地区岩溶发育模式^{[17,18,19,20]}认为该深度段为古岩溶水平潜流带的地下暗河沉积发育,因此连通性较好 ...

2003

0.0

... 南东向呈条带状展布,结合塔河地区岩溶发育模式^{[17,18,19,20]}认为该深度段为古岩溶水平潜流带的地下暗河沉积发育,因此连通性较好 ...

2009

0.0

周江羽, 吕海涛, 林忠民, 等. 塔河油田奥陶系岩溶作用模式及控制因素[J]. 石油实验地质, 2009, 31(6): 547-550.

Karstification research of a complicated anisotrophic carbonate reservoir is presently an important leading field for reservoir sedimenology and geochemistry.Akekule convex included Tahe Oilfield is a long-term developed paleo-uplift based on the pre-Sinian metamorphic basement,which affected by multi-period of Caledonian and Hercynian tectonic uplift and sea-level changes,and superposing reformed by late tectonic movement.A set of Cambrian-Ordovician carbonate karst-fracture-hole reservoirs were developed in Akekule convex.Combined with the karstification and exploration in Tahe Oilfield,three karstification models were established in the area and the key controling factors of karst development were analyzed.

1. Key Laboratory of Tectonics and Petroleum Resources(China University of Geosciences), Ministry of Education, Wuhan, Hubei 430074, China; 2. Design and Planning Institute of Northwest Petroleum Bureau, SINOPEC, Urumqi, Xinjiang 830001, China

碳酸盐岩储层具有异常复杂的非均质性,碳酸盐岩岩溶作用研究是当今储层沉积学和储层地球化学研究的重要前缘领域。塔河油田所处的阿克库勒凸起是在前震旦系变质岩基底上长期发育的一个古隆起,经历了加里东期和海西期多期次的构造抬升和海平面变化影响,并受到后期构造运动的叠加改造,发育了一套寒武—奥陶系碳酸盐岩岩溶—缝洞型储层。结合塔河油田岩溶作用的基本特点和勘探实践,建立了奥陶系碳酸盐岩储层岩溶作用的3种基本模式,并分析了岩溶发育的主要控制因素。

... 南东向呈条带状展布,结合塔河地区岩溶发育模式^{[17,18,19,20]}认为该深度段为古岩溶水平潜流带的地下暗河沉积发育,因此连通性较好 ...

2011

0.0

... 由于声波速度主控的波阻抗参数在一定程度上反映了储集体的综合物性信息^[21],可根据波阻抗与孔隙度的协同关系,将波阻抗数据体转换为反映缝洞储集体等效孔隙度数据体,在此基础上可对研究区物性作出定量评价 ...