基于异常场的地-井瞬变电磁法正演研究

引用本文

徐正玉, 杨海燕, 邓居智, 汤洪志, 张华, 刘旭华, 赵海娇, 巩建军. 基于异常场的地-井瞬变电磁法正演研究[J]. 物探与化探, 2017,39(6): 1176-1182.
XU Zheng-Yu, YANG Hai-Yan, DENG Ju-Zhi, TANG Hong-Zhi, ZHANG Hua, LIU Xu-Hua, ZHAO Hai-Jiao, GONG Jian-Jun. Research on forward simulation of down-hole TEM based on the abnormal field[J]. Geophysical and Geochemical Exploration, 2017,39(6): 1176-1182. 复制到剪切板

Doi:10.11720/wtyht.2015.6.13
Permissions

《物探与化探》编辑部

基于异常场的地-井瞬变电磁法正演研究

徐正玉^1,², 杨海燕^1,², 邓居智², 汤洪志³, 张华², 刘旭华², 赵海娇², 巩建军²

1.东华理工大学放射性地质与勘探技术国防重点学科实验室, 江西南昌 330013

2.东华理工大学核工程与地球物理学院,江西南昌 330013

3.东华理工大学勘察设计院, 江西抚州 344000

杨海燕(1980-),男,博士,副教授,硕士生导师,主要从事电磁法勘探方面的理论与应用研究。E-mail:genious_yang@126.com

作者简介: 徐正玉(1988-),男,东华理工大学在读研究生,研究方向为时间域电磁法勘探。 E-mail: geophysics_xu@163.com

收稿日期: 2015-01-28

基金: 国家自然科学基金项目(41004048,41164003,41304097,41264004); 江西省教育厅科学技术研究项目(GJJ14487); 放射性地质与勘探技术国防重点学科实验室开放基金资助项目(RGET1308)

摘要

在地-井瞬变电磁正演模拟中,前人均以总场为研究对象,分析响应特征。此次选择地-井瞬变电磁异常场为研究对象,对单异常体和多异常体以及在“定源异井”和“动源定井”两种观测方式下典型地电模型进行地-井瞬变电磁法三维正演模拟。首先推导了二次磁场的扩散方程,并用有限差分法进行数值计算。通过分析以地-井瞬变电磁异常场为研究对象,认为异常场能反映目标体空间几何位置参数。研究结果表明:在不同钻孔中接收的异常响应随时间推移而衰减减弱,但异常变化特征保持不变;在不同方位布置场源得到的异常响应差异明显,根据其测量结果可判定异常体空间位置信息。最后总结影响地-井瞬变电磁异常的主要因素有:目标体的埋藏深度、目标体与钻孔之间的耦合关系以及场源的位置关系。研究结果为相关资料解释提供理论参考。

关键词: 地-井瞬变电磁法; 异常场; 正演模拟; 特征分析

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)06-1176-07

Research on forward simulation of down-hole TEM based on the abnormal field

XU Zheng-Yu^1,², YANG Hai-Yan^1,², DENG Ju-Zhi², TANG Hong-Zhi³, ZHANG Hua², LIU Xu-Hua², ZHAO Hai-Jiao², GONG Jian-Jun²

1. Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China Institute of Technology,Nanchang 330013,China

2. School of Nuclear Engineering and Geophysics, East China Institute of Technology, Nanchang 330013,China

3. Survey and Design Institute, East China Institute of Technology, Fuzhou 344000,China

Abstract

In the down-hole TEM forward simulation, previous researchers usually studied total electric field and analyzed response characteristics. In this paper, the authors studied the abnormal field with the down-hole TEM, and simulated the response of single conduction plate and multiple conduction plates. Meanwhile, the down-hole TEM responses of a three-dimensional conductive plate in a typical half space model were simulated to obtain a "fixed source survey at different drill holes" and "fixed drill hole survey at different source places". First, the authors conducted derivation of difference equation of secondary field and made numerical calculation by using the finite difference method. Comparative studies indicate that during the study of the abnormal field in the down-hole TEM, the abnormal field can reflect the position of anomalous space parameters. The results show that the abnormal response of down-hole TEM becomes weaker with time delay, but the abnormal response characteristics remain unchanged in different drill holes, and the abnormal response difference in different source directions is obvious. The measurement results can be used to judge abnormal body space location information. Finally, the main factors that affect the down-hole TEM abnormal response are the depth of the target body, the coupling relationship between the target body and the drill hole and the source position. The research results provide a theoretical basis for interpretation guidelines for related data.

Keyword: down-hole TEM; abnormal field; forward simulation; characteristics

Show Figures

地-井瞬变电磁法(down-hole transient electromagnetic method)采用回线源作为场源, 将探头放入钻孔中, 测量围岩和异常体感应产生的二次场, 通过研究异常场特征得到目标体信息。该方法具有受导电覆盖层和外部电磁干扰小等优点, 被广泛的应用于深部地质调查中^{[1, 2]}。

地-井瞬变电磁法正演是当前研究的热点之一。前人以地-井瞬变电磁总场为研究对象, 如运用积分方程方法研究激发源为长导线源的地-井瞬变电磁法异常特征^{[3, 4]}; 研究激发源为回线源的大地介质影响下的地-井瞬变电磁法异常特征和低阻体异常响应^{[5, 6]}; 分别运用地-井瞬变电磁异常解释系统软件和EMIT Maxwell 4.0软件研究地-井瞬变电磁异常特征, 分析响应特征^{[7, 8]}。国内有关基于异常场地-井瞬变电磁法三维模拟计算的文章则几乎没有。地-井瞬变电磁法可直接测量异常场, 探测井底或井旁盲矿, 但在资料解释时缺少足够的正演资料借鉴, 因此, 基于异常场地-井瞬变电磁法三维正演成为亟待解决的问题。

在前人研究的基础上^{[9, 10, 11, 12, 13, 14, 15, 16]}, 笔者进行了基于异常场地-井瞬变电磁法的三维正演模拟; 从麦克斯韦方程组出发, 运用时域有限差分方法, 推导了二次场地-井瞬变电磁场有限差分格式; 并采用均匀半空间中负阶跃脉冲激发的回线源为激发源, 对均匀半空间中单异常体、多异常体以及在“ 定源异井” 和“ 动源定井” 两种观测方式下地-井瞬变电磁法进行了正演模拟。为了深入分析异常响应, 需要确定响应正负号问题。此次选取阶跃脉冲波激发, 根据楞茨定律, 以目标体为场源激发感应产生的二次场与一次场反向, 规定一次场为正, 则二次场为负, 对二次场场值大小进行分析。

1 差分方程理论基础

1.1 控制方程

在均匀各向同性的介质中, 忽略位移电流条件下, 有源麦克斯韦方程组可以写成下列形式^[17]:

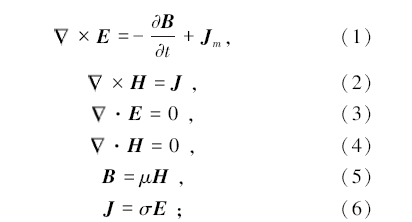
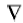
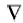
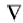
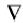
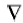
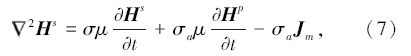
E^p和H^p分别表示一次电场和磁场; E^s和H^s分别表示二次电场和磁场。对式(1)两边取旋度并将式(2)、(3)代入其中, 利用矢量恒等式: × × H= · H- ²H, 化简推导出二次磁场扩散方程

式中:E为电场强度, H为磁场强度, B为磁感应强度, J为电流密度, J_m为磁流密度, μ 和σ 为均匀半空间介质的磁导率和电导率, σ _a为异常体电导率。

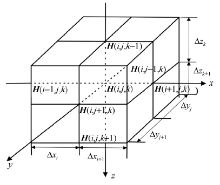
	Figure Option View Download New Window
	图1 三维半空间有限差分网格模型

在直角坐标系下, 采用非均匀网格剖分技术将正演模型计算的区域剖分成若干个小长方体(图1)。将无限大区域空间连续的磁场转化求解有限区域内各个小长方体离散节点的场值。对式(7)两边取体积分:

$\begin{matrix} \begin{matrix} \underset{ΔV}{\int \int \int} (\frac{\partial^{2} h^{s}}{\partial x^{2}} + \frac{\partial^{2} h^{s}}{\partial y^{2}} + \frac{\partial^{2} h^{s}}{\partial z^{2}}) dv = \\ \underset{ΔV}{\int \int \int} (μσ \frac{\partial h^{s}}{\partial t} + μ σ_{a} \frac{\partial h^{p}}{\partial t} - σ_{a} j_{m}) dv, (8) \end{matrix} \end{matrix}$

应用Gauss公式对式(8)进行化简, 磁场对空间、时间的偏导数以中间差商近似代替, 选用稳定收敛的Dufort-Frankel法进行差分离散。最后, 经化简整理得^[18]:

$\begin{matrix} \begin{matrix} H_{i, j, k}^{s, n + 1} = & \frac{1 - 6 {\overset{̅}{r}}_{i, j, k}}{1 + 6 {\overset{̅}{r}}_{i, j, k}} H_{i, j, k}^{s, n - 1} + \\ \frac{2 r_{i, j, k}^{x}}{1 + 6 {\overset{̅}{r}}_{i, j, k}} [\frac{Δ x_{i + 1}}{Δ {\overset{̅}{x}}_{i}} H_{i - 1, j, k}^{s, n} + \frac{Δ x_{i + 1}}{Δ {\overset{̅}{x}}_{i}} H_{i + 1, j, k}^{s, n}] + \\ \frac{2 r_{i, j, k}^{y}}{1 + 6 {\overset{̅}{r}}_{i, j, k}} [\frac{Δ y_{j + 1}}{Δ {\overset{̅}{y}}_{j}} H_{i, j - 1, k}^{s, n} + \frac{Δ y_{j + 1}}{Δ {\overset{̅}{y}}_{j}} H_{i, j + 1, k}^{s, n}] + \\ \frac{2 r_{i, j, k}^{z}}{1 + 6 {\overset{̅}{r}}_{i, j, k}} [\frac{Δ z_{k + 1}}{Δ {\overset{̅}{z}}_{k}} H_{i, j, k - 1}^{s, n} + \frac{Δ z_{k + 1}}{Δ {\overset{̅}{z}}_{k}} H_{i, j, k + 1}^{s, n}] + \\ \frac{μ {\overset{̅}{σ}}_{a, i, j, k}}{2 (1 + 6 {\overset{̅}{r}}_{i, j, k}) Δt} [H_{i, j, k}^{p, n - 1} - H_{i, j, k}^{p, n + 1}] - \frac{nμS {\overset{̅}{σ}}_{a, i, j, k}}{1 + 6 {\overset{̅}{r}}_{i, j, k}} \frac{dI (t)}{dt}, (9) \end{matrix} \end{matrix}$

式中:Δ $\begin{matrix} {\overset{̅}{x}}_{i} \end{matrix}$ =(Δ x_i+Δ x_i+₁)/2, Δ $\begin{matrix} {\overset{̅}{y}}_{j} \end{matrix}$ =(Δ y_j+Δ y_j+₁)/2,

Δ $\begin{matrix} {\overset{̅}{z}}_{k} \end{matrix}$ =(Δ z_k+Δ z_k+₁)/2, $\begin{matrix} r_{i, j, k}^{x} \end{matrix}$ =Δ t/(μ $\begin{matrix} {\overset{̅}{σ}}_{i, j, k} \end{matrix}$ Δ x_iΔ x_i+₁),

$\begin{matrix} r_{i, j, k}^{y} \end{matrix}$ =Δ t/(μ $\begin{matrix} {\overset{̅}{σ}}_{i, j, k} \end{matrix}$ Δ y_jΔ y_j+₁), $\begin{matrix} r_{i, j, k}^{z} \end{matrix}$ =Δ t/(μ $\begin{matrix} {\overset{̅}{σ}}_{i, j, k} \end{matrix}$ Δ z_kΔ z_k+₁),

$\begin{matrix} {\overset{̅}{σ}}_{i, j, k} \end{matrix}$ = $\begin{matrix} \frac{1}{(Δ x_{i} + Δ x_{x + 1}) (Δ y_{j} + Δ y_{j + 1}) (Δ z_{k} + Δ z_{k + 1})} \end{matrix}$ [σ _i_,_j_,_kΔ x_iΔ y_jΔ z_k+σ _i+_1,_j_,_kΔ x_i+₁Δ y_jΔ z_k+σ _i_,_j+_1,_kΔ x_iΔ y_j+₁Δ z_k+σ _i+_1,_j+_1,_kΔ x_i+₁Δ y_j+₁Δ z_k+σ _i_,_j_,_k+₁Δ x_iΔ y_jΔ z_k+₁+σ _i+_1,_j_,_k+₁Δ x_i+₁Δ y_jΔ z_k+₁+σ _i_,_j+_1,_k+₁Δ x_iΔ y_j+₁Δ z_k+₁+σ _i+_1,_j+_1,_k+₁Δ x_i+₁Δ y_j+₁Δ z_k+₁] 。

1.2 初始条件与边界条件

在正演计算中, 初始条件一般选取均匀半空间中场源的解析解代入计算, 场源的形式可以根据实际需要进行选择^[2]。选取回线源作为初始条件代入, 均匀半空间中时间域回线源解析解可以由频率域解析解进行反拉普拉斯转换得到。频率域中回线源磁场垂直分量的解析解为^[17]

$\begin{matrix} H_{z} = - \frac{I}{k^{2} a^{3}} [3 - (3 + 3 ika - k^{2} a^{2}) e^{- ika}], (10) \end{matrix}$

其中, I为供电电流大小, k为波数, a为发射回线半径。根据逆拉普拉斯变换公式, 将谐变场表达式转换到瞬变场中

$\begin{matrix} \frac{\partial H_{z}}{\partial t} = - \frac{I}{μ_{0} σ a^{3}} [3 \erf (θa) - \frac{2}{\sqrt{π}} (3 θa + 2 θ^{3} a^{3})] e^{- θ^{2} a^{2}} (11) \end{matrix}$

其中:erf为误差函数, θ = $\begin{matrix} \sqrt{μ_{0} σ / 4 t} \end{matrix}$ , 初始时间步长应该满足

$\begin{matrix} Δ t_{\max} = μmin ({\overset{̅}{σ}}_{i, j, k}) mi n^{2} (Δ) / 6, \end{matrix}$

式中, min(Δ )为计算模型中最小网格步长。

在地-空边界上, 将边界区域近似看成无穷远, 采用向上延拓方法处理; 在侧面和底面边界条件选取上, 采用了修正的廖氏吸收边界条件进行计算。该边界条件对边界处磁场处理比较好并且在计算区域和内部不会产生磁场畸变^{[18, 19]}。修正的廖氏吸收边界条件公式为

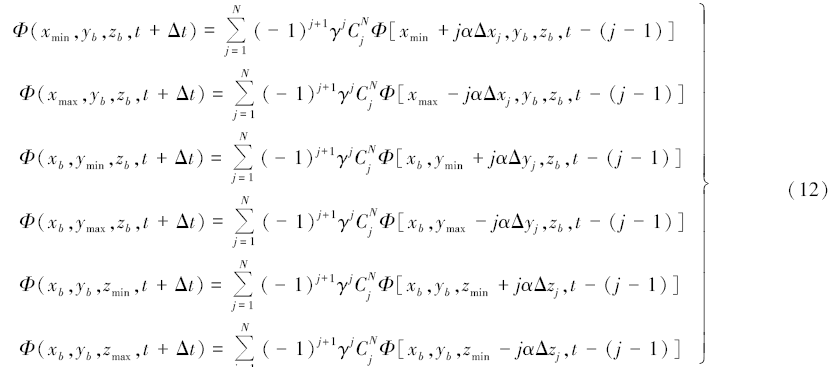
式中:C为电磁波波速, α 是控制吸收角度的实参数, N为阶数, r为反射系数, $\begin{matrix} C_{j}^{N} \end{matrix}$ 为二项系数。

2 三维正演模拟

2.1 单异常体地-井TEM响应

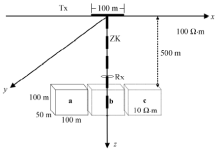
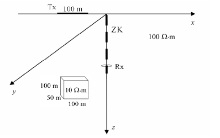
图2为单异常体三维地质模型。在直角坐标系下, 设置三维均匀半空间介质大小为500 m× 500 m× 1 000 m, 有限差分网格节点为51× 51× 101。异常体电阻率为10 Ω · m, 几何模型长、宽、高分别为100 m× 50 m× 100 m, 围岩电阻率为 100 Ω · m。图中a、b、c分别表示异常体位于地下三个不同位置; 黑色虚线表示钻孔位置, 场源中心与钻孔位置重合; 回线源边长为100 m, 电流大小为10 A。需要说明的是:在本文中, 选取异常响应幅值大小进行分析, 忽略响应的正负号问题, 所以响应均为正。

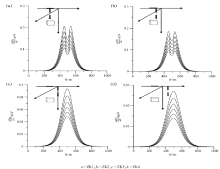
	Figure Option View Download New Window
	图2 单个低阻体三维模型

图3是在均匀半空间中低阻体模型处于不同位置时地-井TEM的响应曲线(0.964 ~0.982 ms)。图中显示:当断开供电电流, 由于电磁感应作用, 回线源激发的电磁场在水平低阻体表面产生感应电流, 形成以低阻体为场源的二次场, 钻孔中接收的二次场响应曲线能清楚地表明低阻体的埋深位置; 当低阻体水平位于钻孔左右两侧且距离钻孔之间距离相等时, 感应产生的异常响应值是相等的, 异常响应曲线在低阻体对应深度呈现相同的响应值。在图3b中, 异常响应曲线呈现两个极大值和一个极小值, 且极大值几乎是图3a、c中极大值的10倍。这是因为:该情况下低阻体与场源耦合关系最佳, 测量到的异常最强; 当断开发射线圈中供电电流时, 一次场开始减弱衰减, 受电磁感应作用影响, 一次场在低阻体上下表面内感应生成电磁场, 形成以低阻体为场源的二次场; 低阻体垂直高度为100 m, 所以在 -450 m 和-550 m处, 形成感应曲线的极大值; 受低阻体上下表面感应磁场相互叠加的影响, 在-500 m 处形成感应曲线极小值。

	Figure Option View Download New Window
	图3 单异常体地-井TEM响应曲线

2.2 多异常体地-井TEM响应

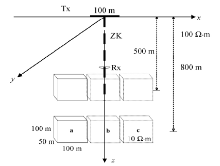
图4多异常体三维地质模型。图中上下两个异常体为一组, 异常体之间垂直高度相距300 m, 其他模型参数均与图2一致。

	Figure Option View Download New Window
	图4 多个低阻体的三维模型

图5是图4所示地电模型的响应曲线(0.964~0.982 ms)。图中显示:在晚期钻孔中接收的低阻体感应产生电磁场响应均能清楚明显的表明低阻体埋深位置。从图5a、c中看出, 在-500 m处对应的极大值与图3中是一致的, 衰减规律相同; 在-800 m处, 因为低阻体埋深增加, 在响应曲线上表示为异常幅值减小, 但均能表明低阻体在空间的几何位置。

	Figure Option View Download New Window
	图5 多个低阻体不同位置下的地-井TEM响应曲线

从图5b看出, 在低阻体耦合条件最佳的情况下, 响应的极大值几乎是图5a、c中的10倍, 在450 m和550 m、750 m和850 m处, 形成感应曲线的极大值; 在500 m和800 m, 受低阻体上下表面感应磁场相互叠加的影响, 在响应曲线上形成极小值。

2.3 定源异井观测方式下的地-井TEM响应

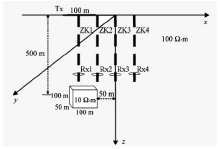
图6为定源异井观测方式下三维地质模型。设网格剖分参数和低阻体几何参数同图2中一致, 图中主剖面上有4口钻孔, 钻孔之间相距50 m, 场源位于ZK1正上方, 其余参数同上。

	Figure Option View Download New Window
	图6 定源异井观测方式三维模型

图7是在图6地电模型下, 在ZK1~ZK2中接收6个时刻的响应曲线(0.964~0.982 ms)。从图中曲线分析得出:在图7a、b中, 钻孔位置分别是位于异常体正上方和异常体边缘处, 并都穿过异常体, 所以, 接收的响应为双峰异常特征, 且双峰异常在横坐标上对应的深度与异常体上下表面对应的位置重合; 低阻体异常响应极大值随时间推移而衰减减弱, 但异常变化特征保持不变, 当钻孔穿过低阻体时, 观测的异常响应幅值最大, 随着钻孔离异常体距离慢慢增加时, 观测的异常响应幅值逐渐减弱, 在数值上几乎减小了10倍。

	Figure Option View Download New Window
	图7 不同井位观测的低阻体地-井TEM响应曲线

2.4 动源定井观测方式下的地-井TEM响应

图8为场源位于左侧时动源定井观测方式下三维地质模型, 模型参数与上述设置一致, 设场源位于钻孔左侧50 m处。

	Figure Option View Download New Window
	图8 动源定井观测方式三维模型(源在左侧)

图9为均匀半空间中低阻体处于不同位置时的响应曲线(0.964~0.982 ms)。可以看出, 当断开供电电流, 由于电磁感应作用, 回线源激发的电磁场在低阻体内产生感应电流, 形成以低阻体为场源的二次场, 从钻孔中接收的二次场响应曲线能清楚明显的表明低阻体埋深位置。

对比图9a、b可以看出, 当低阻体距离钻孔的距离在增加时, 接收到的异常响应几乎减弱一倍; 从图9a、c可以看出, 当低阻体距离场源的垂直距离增加时, 接收的异常响应减弱至很小, 则在深部接收的异常响应弱。因此, 当场源位置不变时, 地-井瞬变电场二次场异常响应随着低阻体与钻孔之间距离增加或低阻体埋深距离增加而减弱。

	Figure Option View Download New Window
	图9 低阻体不同位置时的地-井TEM响应曲线(源在左侧)

对场源位于钻孔右侧时的水平低阻体(图10)进行数值模拟, 低阻体和围岩电阻率参数不变, 通过改变场源位置, 进行对比模拟研究。场源位于钻孔右侧50 m处激发。

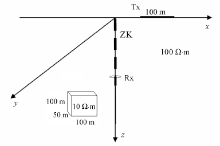	Figure Option View Download New Window
	图10 动源异井观测方式三维模型(源在右侧)

图11是均匀半空间中场源位于钻孔右侧时, 低阻体处于不同位置时的响应曲线(0.964~0.982 ms)。可以看出, 当场源位于右侧时, 断开电流, 在低阻体内感应产生的二次场。在相同的观测时间内, 从钻孔中接收的二次场响应幅值减小, 但响应曲线也能清楚地表明低阻体埋深位置。对比图10和图11:在低阻体位置、电阻率等信息不变情况下, 当场源位于右侧时, 在钻孔中接收的响应明显减弱, 但是异常响应形态保持相同。

	Figure Option View Download New Window
	图11 低阻体不同位置时的地-井TEM响应曲线(源在右侧)

综上所述, 在钻孔中接收到瞬变电磁异常场能表明异常体的位置, 通过分析响应曲线, 可以得到异常体空间位置等信息。对异常响应曲线分析得出, 地-井瞬变电磁异常主要受场源位置, 目标体埋藏深度和目标体与钻孔之间相对距离影响。

3 结论

研究了基于异常场地-井瞬变电磁法三维正演模拟, 以二次磁场差分离散方程为基础, 选取回线源为场源, 选用精度高的修正后廖式吸收边界条件。对单异常体和多异常体以及在“ 定源异井” 和“ 动源定井” 两种观测方式下地-井瞬变电磁法进行正演模拟。通过对比分析得出:

1) 地-井瞬变电磁异常场能反映异常体空间几何位置, 判断异常体与钻孔之间几何位置关系。

2) 在不同钻孔中接收的异常响应随时间推移而衰减减弱, 但异常变化特征保持不变。观测的异

常响应随着钻孔离异常体距离慢慢增加而逐渐减弱。在不同方位布置场源得到的异常响应差异明显, 根据其测量结果可判定异常体空间位置信息。

3) 地-井瞬变异常响应主要受目标体的埋藏深度、目标体与钻孔之间的耦合关系以及场源的位置影响。在场源位置不变时, 异常体埋藏越深, 异常响应越弱; 目标体与钻孔之间耦合最佳时, 异常响应越强; 当异常体埋深位置和距离钻孔位置不变, 当场源位于钻孔左右不同方位时, 异常响应差异明显。

此次研究工作可为定性解释地-井TEM异常提供参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	蒋邦远. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 1998. [本文引用:1]
[2]	牛之琏. 时间域电磁法勘探[M]. 长沙: 中南大学出版社, 2007. [本文引用:2]
[3]	Eaton P A, Hohmann G W. The influence of a conductive host on two-dimensional borehole transient electromagnetic responses[J]. Geophysics, 1984, 49(7): 861-869. [本文引用:1]
[4]	West R C, Ward S H, The borehole transient electromagnetic response of a three-dimensional fracture zone in a conductive half-space[J]. Geophysics, 1988, 53(11): 1469-1478. [本文引用:1]
[5]	孟庆鑫, 潘和平. 地-井瞬变电磁响应特征数值模拟分析[J]. 地球物理学报, 2012, 55(3): 1046-1053. [本文引用:1]
[6]	孟庆鑫, 潘和平, 牛峥. 大地介质影响下地-井瞬变电磁的正演模拟研究[J]. 中国矿大学报, 2014, 43(6): 1113-1119. [本文引用:1]
[7]	张杰. 地-井瞬变电磁异常特征分析及矢量交会解释方法[D]. 北京: 中国地质大学(北京), 2009. [本文引用:1]
[8]	戴雪平. 地-井瞬变电磁法三维响应特征研究[D]. 北京: 中国地质大学(北京), 2013. [本文引用:1]
[9]	宋维琪. 3D瞬变电磁场有限差分正演计算[J] . 石油地球物理勘探, 2000, 35(6) : 751-756. [本文引用:1]
[10]	闫述, 陈明生, 傅君眉. 瞬变电磁场的直接时域数值分析[J] . 地球物理学报, 2002, 45(2): 275-284. [本文引用:1]
[11]	杨海燕, 岳建华. 磁偶源2. 5维瞬变电磁场全空间FDTD数值模拟[J]. 物探与化探, 2008, 32(3): 326-330 [本文引用:1]
[12]	岳建华, 杨海燕, 胡搏. 矿井瞬变电磁法三维时域有限差分数值模拟[J]. 地球物理学进展. 2007, 22(6): 1904-1909. [本文引用:1]
[13]	董浩, 魏文博, 叶高峰, 等. 基于有限差分正演的带地形三维大地电磁反演方法[J]. 地球物理学报, 2014, 57(3): 939-952. [本文引用:1]
[14]	孙怀风, 李貅, 李术才, 等. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J]. 地球物理学报, 2013, 56(3): 1049-1064. [本文引用:1]
[15]	谭捍东, 余钦范, John Booker, 等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003, 46(5): 705-711. [本文引用:1]
[16]	杨海燕, 邓居智, 张华等. 矿井瞬变电磁法全空间视电阻率解释方法研究[J]. 地球物理学报, 2010, 53(3): 651-656. [本文引用:1]
[17]	米萨克N 纳比吉安. 勘查地球物理电磁法(一)[M]. 赵经祥, 王艳君, 译. 北京: 地质出版社, 1992. [本文引用:2]
[18]	杨海燕. 矿用多匝小回线源瞬变电磁场数值模拟与分布规律研究[D]. 徐州: 中国矿业大学, 2009. [本文引用:2]
[19]	廖振鹏, 周正华, 张艳红. 波动数值模拟中透射边界的稳定实现[J]. 地球物理学报, 2002, 45(4): 533-545. [本文引用:1]

1998

0.0

... 该方法具有受导电覆盖层和外部电磁干扰小等优点,被广泛的应用于深部地质调查中^[1,2] ...

2007

0.0

... 该方法具有受导电覆盖层和外部电磁干扰小等优点,被广泛的应用于深部地质调查中^[1,2] ...

... 2 初始条件与边界条件在正演计算中,初始条件一般选取均匀半空间中场源的解析解代入计算,场源的形式可以根据实际需要进行选择^[2] ...

1984

0.0

... 前人以地-井瞬变电磁总场为研究对象,如运用积分方程方法研究激发源为长导线源的地-井瞬变电磁法异常特征^[3,4] ...

1988

0.0

... 前人以地-井瞬变电磁总场为研究对象,如运用积分方程方法研究激发源为长导线源的地-井瞬变电磁法异常特征^[3,4] ...

2012

0.0

... 研究激发源为回线源的大地介质影响下的地-井瞬变电磁法异常特征和低阻体异常响应^[5,6] ...

2014

0.0

... 研究激发源为回线源的大地介质影响下的地-井瞬变电磁法异常特征和低阻体异常响应^[5,6] ...

0.0

... 0软件研究地-井瞬变电磁异常特征,分析响应特征^[7,8] ...

0.0

... 0软件研究地-井瞬变电磁异常特征,分析响应特征^[7,8] ...

2000

0.0