适于大规模数据的逆时偏移实现方案

引用本文

张慧宇, 王立歆, 孔祥宁, 李博. 适于大规模数据的逆时偏移实现方案[J]. 物探与化探, 2015,39(5): 978-984.
ZHANG Hui-Yu, WANG Li-Xin, KONG Xiang-Ning, LI Bo. The implementation scheme of reverse-time migration for mass seismic data[J]. Geophysical and Geochemical Exploration, 2015,39(5): 978-984.
Doi:10.11720/wtyht.2015.5.17 复制到剪切板

Permissions

《物探与化探》编辑部

适于大规模数据的逆时偏移实现方案

张慧宇, 王立歆, 孔祥宁, 李博

中石化石油物探技术研究院,江苏南京 211103

作者简介: 张慧宇(1983-),女,工程师,运筹学与控制论专业,现从事地震偏移成像与高性能计算研究工作。E-mail:zhanghy.swty@sinopec.com

收稿日期: 2015-01-06

基金: 国家自然科学基金青年基金项目(41204073)

摘要

针对海量地震数据逆时偏移所面临的问题和挑战,解决逆时偏移海量计算和海量存储需求在CPU/GPU异构集群平台上实现时的技术瓶颈,重点介绍了基于GPU-RDMA直接通信技术和GPU-Stream流技术的并行算法,形成适合于GPU集群的大规模分布式并行计算,即高密度采集地震数据的三维叠前逆时偏移计算技术;应用高密度实际地震数据测试,计算效率可提升15~40倍。

关键词: 逆时偏移; 直接通信; 流技术; 计算效率; 并行算法

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)05-0978-07 doi: 10.11720/wtyht.2015.5.17

The implementation scheme of reverse-time migration for mass seismic data

ZHANG Hui-Yu, WANG Li-Xin, KONG Xiang-Ning, LI Bo

SINOPEC Geophysical Researcher Institute,Nanjing 211103,China

Abstract

In view of the problems and challenges in pre-stack reverse-time depth migration (RTM) for mass seismic data,the paper focuses on introducing GPU-RDMA and GPU-Stream,which are used to solve the large calculation cost and the mass memory demand of RTM on the CPU/GPU heterogeneous platform,and develops the RTM suitable for large-scale distributed parallel computing in GPU clusters.This technology can be used to deal with the high density seismic data,and the results of actual seismic data application show that the computing efficiency is up to 15~40 times.

Keyword: reverse-time migration; direct communication; stream; computing efficiency; parallel algorithm

Show Figures

随着勘探开发程度的不断深入, 地震资料处理对偏移成像的要求越来越高。目前, 叠前深度偏移是成像精度最高的一类方法, 在工业界应用最多的主要有基于射线理论的Kirchhoff积分法和基于单程波动理论的波动方程两类叠前深度偏移方法。Kirchhoff 积分偏移算法的理论是基于波场高频近似, 而它的实现通常应用了单走时路径的假设, 从而使得该技术不适用于速度横向变化剧烈的介质的高精度成像; 而单程波动方程偏移算法的理论来源于对全声波方程的单程波逼近, 其有效的数值实现需要对描述单程波的拟微分方程实行进一步地简化, 进而导致了该偏移算法存在偏移倾角限制, 不适应高陡构造成像。

基于全声波方程的逆时叠前深度偏移(pre-stack reverse-time depth migration, RTM)^[1]是具有明确地质意义的精确成像方法。它通过描述地震波在复杂介质传播过程中的波场延拓算子进行叠前深度偏移成像, 物理概念清晰, 更稳健、更精确, 能处理多路径问题以及由速度变化引起的聚焦或焦散效应, 并具有很好的保幅性; 不需要进行上、下行波场分离, 对波动方程的近似较少, 从而克服了偏移倾角和偏移孔径的限制, 并将Kirchhoff方法和单程波动方程方法的优点汇集于一身, 可以有效地适应纵横向存在剧烈变化的地下介质。该技术具有相位准确、成像精度高、对介质横向速度变化和高陡倾角适应性强, 甚至可以利用回转波、多次波正确成像等优点, 是目前理论最先进、成像精度最高的地震偏移成像方法。由于该技术计算量、存储需求量巨大这些瓶颈问题不易解决, 导致RTM一直没有应用于生产。直到近期, 随着高性能计算机及其应用技术的发展, 许多学者对该方法进行了大量卓有成效的研究工作, 使其逐步走向工业化。Symes^[2]提出CheckPointing方法, 在增加一定计算量的基础上减少波场的存储需求; Robert^[3]提出用随机边界条件代替吸收边界条件, 通过增加一次波场反传重建波场的方式来实现相关成像条件, 可以完全消除波场存储问题, 但在实际应用过程中, 随机边界条件通常在剖面中带来一些随机干扰, 影响成像质量; Feng^[4]提出一种新的波场重构策略, 通过成像体四周波场反传来重构整个成像空间的波场, 利用该策略实现逆时偏移, 边界条件仍然使用常规的吸收边界, 计算量、存储量以及成像效果均基本满足要求。

当前高性能领域最流行的加速器GPU(graphic processing unit), 以其强大的计算性能, 不断改善的编程界面吸引了来自众多非图形计算领域的关注, 是一种极具发展潜力的处理器体系结构^[5]。目前GPU已在高性能计算领域取得了广泛的应用, 利用GPU进行浮点运算加速的通用计算(general purpose computation on GPUs, GPGPU)也成为计算机应用领域的一个热点研究方向。CPU-GPU 异构系统兼具多方面的优势:其一, 通用微处理器处理标量计算, 提供通用计算能力, 使得异构系统可以适应多方面的应用; 其二, GPU面向某些特定的领域可以提供强大的计算性能, 且能效比较高, 使得异构系统比同构系统拥有更高的性能和效能。

利用GPU的强大计算能力进行逆时偏移成像, 国内外众多学者已经进行了大量的研究探索。如Micikevicius等^[6]研究了基于CUDA平台的有限差分实现问题, 给出了快速实现有限差分的算法。Foltinek等^[7]讨论了生产规模数据的逆时偏移在GPU上实现的挑战, 讨论了区域分解进行的必要性。国内研究人员也对GPU在地球物理上的应用进行了大量研究, 早在2007年, 赵改善^[8]就提出了将GPU应用于地球物理计算中; 2008年, 张兵等^[9]实现了基于CUDA的二维叠前深度偏移技术; 李肯立等^[10]实现了基于CUDA的叠前时间偏移技术。在逆时偏移方面, 刘红伟等^[11]进行了二维高阶差分GPU逆时偏移; 赵磊等^[12]进行了三维逆时偏移的GPU实现; 李博等^[13]对比分析了基于CPU/GPU平台的逆时偏移实现策略; 刘守伟等^[14]比较系统地阐述了GPU逆时偏移的相关问题; 他们都是以常规地震数据为基础设计逆时偏移的实现策略。文中针对海量地震数据逆时偏移多卡协同计算的通信问题, 采用基于GPU-RDMA直接通信技术和GPU-Stream流技术的并行算法, 形成适合于GPU集群的大规模分布式并行计算, 有效地解决了逆时偏移海量计算和海量存储需求在CPU/GPU异构集群平台上实现时的技术瓶颈。应用笔者所提出的适用于大规模数据的RTM技术对高密度实际地震数据进行测试, 相对于CPU-RTM计算效率可提升15~40倍。

1 海量数据逆时偏移算法的GPU实现策略

1.1 高阶有限差分法逆时波场传播算子

在密度恒定的各向同性完全弹性介质中, 地震波的传播波场满足双程波方程

$\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}} = \frac{1}{v^{2} (x, y, z)} \frac{\partial^{2} u}{\partial t^{2}}, (1) \end{matrix}$

其中:u(x, y, z, t)为地表记录的压力波场, v(x, y, z)为纵横向可变的介质速度。

逆时偏移的核心归根到底是正演问题, 选取一种计算精度好、效率高的算法是十分必要的。现有的地震波模拟手段有:有限差分法、有限元法和伪谱法。有限差分法具有算法简单快速, 能自动适应速度场的任意变化的优势, 仍然是主要方法。

当利用传统的截断误差为O(Δ x², Δ y², Δ z², Δ t²)的差分格式时, 为保证频散较小及递推过程稳定, 差分网格要求取得非常小, 这样计算需要的内存及运算时间会大大增加。Dablain于1986年^[15]提出利用高阶差分方程来进行上述模拟和偏移过程。利用高阶差分方程时, 网格值可以取得大些, 而计算精度并不降低。式(2)为时间四阶、空间M阶(一般要求大于4)、截断误差为O(Δ x^M, Δ y^M, Δ z^M, Δ t⁴)的三维正演模拟高阶差分方程:

$\begin{matrix} \begin{matrix} u_{i, j, k}^{n + 1} = 2 u_{i, j, k}^{n} - u_{i, j, k}^{n - 1} + \frac{1}{2} {(\frac{vΔt}{Δx})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i + m, j, k}^{n} + u_{i - m, j, k}^{n})] + \\ \frac{1}{2} {(\frac{vΔt}{Δy})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i, j + m, k}^{n} + u_{i, j - m, k}^{n})] + \frac{1}{2} {(\frac{vΔt}{Δz})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i, j, k + m}^{n} - u_{i, j, k - m}^{n})] + \\ \frac{1}{6} \frac{v^{4} Δ t^{4}}{Δ x^{2} Δ y^{2}} [(u_{i + 1, j + 1, k}^{n} - 2 u_{i, j + 1, k}^{n} + u_{i - 1, j + 1, k}^{n}) - 2 (u_{i + 1, j, k}^{n} - 2 u_{i, j, k}^{n} + u_{i - 1, j, k}^{n}) + (u_{i + 1, j - 1, k}^{n} - 2 u_{i, j - 1, k}^{n} + u_{i - 1, j - 1, k}^{n})] + \\ \frac{1}{6} \frac{v^{4} Δ t^{4}}{Δ y^{2} Δ z^{2}} [(u_{i, j + 1, k + 1}^{n} - 2 u_{i, j, k + 1}^{n} + u_{i, j - 1, k + 1}^{n}) - 2 (u_{i, j + 1, k}^{n} - 2 u_{i, j, k}^{n} + u_{i, j - 1, k}^{n}) + (u_{i, j + 1, k - 1}^{n} - 2 u_{i, j, k - 1}^{n} + u_{i, j - 1, k - 1}^{n})] + \\ \frac{1}{6} \frac{v^{4} Δ t^{4}}{Δ z^{2} Δ x^{2}} [(u_{i + 1, j, k + 1}^{n} - 2 u_{i, j, k + 1}^{n} + u_{i - 1, j, k + 1}^{n}) - 2 (u_{i + 1, j, k}^{n} - 2 u_{i, j, k}^{n} + u_{i - 1, j, k}^{n}) + (u_{i + 1, j, k - 1}^{n} - 2 u_{i, j, k - 1}^{n} + u_{i - 1, j, k - 1}^{n})] + \\ \frac{1}{12} \frac{v^{4} Δ t^{4}}{Δ x^{4}} [u_{i + 2, j, k}^{n} + u_{i - 2, j, k}^{n} - 4 (u_{i - 1, j, k}^{n} + u_{i + 1, j, k}^{n}) + 6 u_{i, j, k}^{n}] + \\ \frac{1}{12} \frac{v^{4} Δ t^{4}}{Δ y^{4}} [u_{i, j + 2, k}^{n} + u_{i, j - 2, k}^{n} - 4 (u_{i, j - 1, k}^{n} + u_{i, j + 1, k}^{n}) + 6 u_{i, j, k}^{n}] + \\ \frac{1}{12} \frac{v^{4} Δ t^{4}}{Δ z^{4}} [u_{i, j, k + 2}^{n} + u_{i, j, k - 2}^{n} - 4 (u_{i, j, k - 1}^{n} + u_{i, j, k + 1}^{n}) + 6 u_{i, j, k}^{n}] 。 (2) \end{matrix} \end{matrix}$

式(2)有关于时间的4阶偏导数项, 如果直接解, 涉及到的时间层过多, 所需储存的波场多, 计算效率低。当要求时间方向的差商保持O(Δ t²)的截断误差时, 式(2)会简化很多。而且这样做并不会对正演或偏移结果产生很大的影响。时间二阶、空间M阶、截断误差为O(Δ x^M, Δ y^M, Δ z^M, Δ t²)的三维正演模拟高阶差分方程为

$\begin{matrix} \begin{matrix} u_{i, j, k}^{n + 1} = 2 u_{i, j, k}^{n} - u_{i, j, k}^{n - 1} + \\ \frac{1}{2} {(\frac{vΔt}{Δx})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i + m, j, k}^{n} + u_{i - m, j, k}^{n})] + \\ \frac{1}{2} {(\frac{vΔt}{Δy})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i, j + m, k}^{n} + u_{i, j - m, k}^{n})] + \\ \frac{1}{2} {(\frac{vΔt}{Δz})}^{2} [ω_{0} u_{i, j, k}^{n} + \overset{M / 2}{\sum_{m = 1}} ω_{m} (u_{i, j, k + m}^{n} + u_{i, j, k - m}^{n})] 。 (3) \end{matrix} \end{matrix}$

逆时偏移在算法实现上主要包括三个关键技术, 即震源波场的正向延拓、接收点波场的反向延拓和恰当的成像条件。震源波场与接收点波场利用高阶差分方程进行模拟和偏移, 需要巨大的计算量; 震源波场是从t₀时刻向下正向延拓的, 为了与接收点波场进行零延迟互相关, 就必须保存t₀到t_n各个时刻的震源波场, 然后随接收点波场反向延拓作零延迟互相关成像计算, 这是一个巨大的存储需求。为了解决这一个问题, 采用震源波场重构的存储策略, 以计算换存储, 即进行波场重构时的存储策略, 先将震源波场正向延拓到t_n时刻, 每步延拓只存储波场边界信息; 在接收点波场进行反向延拓时作为边界条件重构震源波场, 应用成像条件进行互相关成像。

1.2 逆时偏移并行算法设计

RTM具有计算密集、计算海量的特点, 对计算机的性能要求非常高。近年来GPU作为新兴的计算模式, 体现出较强的优势, 逐渐得到了应用。地震叠前逆时深度偏移是典型的大计算吞吐、大数据吞吐的地震数据处理任务, 须采用并行计算的策略来实现实际的应用; 而RTM问题中所固有的可分解性和线性叠加性质, 使其具有良好的并行能力, 这为实现RTM的并行计算提供了条件。有限差分法进行波场外推是典型的单指令多数据的计算, 非常适合用GPU处理, 例如nVidia Tesla Kepler K10有2 688个核心, 可以同时处理2 688个样本, 尤其是RTM的单精度计算, 具有非常高的处理效率。GPU/CPU协同并行计算就是将GPU和CPU两种不同架构的处理器结合在一起, 组成硬件上的协同并行模式, 同时在应用程序编写上实现GPU和CPU软件协同配合的并行计算。CPU主要负责GPU的控制、数据的准备、数据在节点间的发送与接收等, 即进行并行控制; GPU主要进行RTM中最耗时的波场外推计算及并行计算。

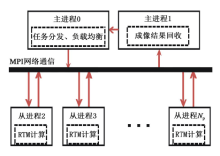
RTM计算以单个炮集数据为基本计算单元, 对于每一炮数据来说, 进行RTM成像都是一个相对独立的计算过程, 计算时相互之间没有数据交换, 可作为一个独立的作业, 具有很强的并行性。是典型的单指令多数据(SPMD)算法, 即用相同的程序在不同的节点上对不同的数据体进行计算。每个节点(进程)上的计算任务不一定同时开始或结束, 各个节点(进程)间的任务相互无关。我们采用了双主进程的并行计算模式, 其中一个主进程负责任务分配的实现; 另一个主进程作成像结果规约计算。这种输入和输出分离(图1)的并行控制模式, 可以有效地提高程序的稳定性和容错能力。负责分发作业的主进程给各个计算节点(进程)发送一个计算任务, 由于各节点上相同程序不同数据的计算或通信并不是同时进行的, 当计算节点上作业做完后, 即得到一份新的作业, 便又立即开始执行, 这大大增加了计算相对于通信的比重, 有效地提高了计算的效率。该主进程在考虑到计算节点间性能的差异及多用户运行环境下, 可最大限度地发挥各个节点的计算效率, 来保证RTM计算时的动态负载均衡。而负责规约收集的主进程, 在设定的任务点上收集各个计算节点(进程)的中间结果, 使输入与输出的通信分离, 同时可易于实现RTM计算过程中的断点保护。

	Figure Option View Download New Window
	图1 实现RTM的双主从并行计算模式

具体的实现过程是:首先, 主进程0负责地震数据的分发和任务分配, 主进程1负责成像结果的规约; 其次, 从进程接收一个计算任务后进行RTM深度偏移成像, 计算完毕后发送结果给1号主进程, 等待下一个任务的到来, 直到所有的任务完成; 最后, 1号进程收集完毕各个从进程的计算结果, 输出最终RTM成像结果。

1.3 逆时偏移算法的多GPU卡通信技术

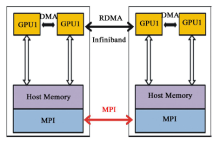
当数据量较大时, GPU单卡显存已经不能满足一炮数据的存储量需求。为了解决这一难题, 我们采用多卡联合作业模式。首先将数据空间划分成N块, 每块GPU卡计算其中一块。此时相应的逆时偏移计算模式也较复杂。这种情况下, 不仅需要GPU与主机间进行数据传输, 还需要GPU卡之间进行数据交换。而GPU卡之间是不能直接进行数据传输的, 只能通过主机这一桥梁进行数据交换, 因此增加了计算的复杂度和数据I/O量。该计算模式如图2所示。

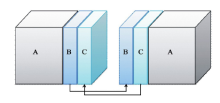
	Figure Option View Download New Window
	图2 GPU-RTM多卡联合计算模式(数据通信)

为了使算法满足任意大规模地震数据的处理, 我们设计了利用内存作为中转站的数据交换机制, 这种机制不限定每个节点GPU卡的数量, 根据计算需求动态规划每炮计算需要的节点数和GPU卡的数量。这样, 一次数据交换, 就需要4次GPU与CPU之间的数据传输, 以及一次CPU内存间的传输, 其中CPU与GPU的数据I/O具有一定的访存延迟。一方面, 通过GPU多卡处理可以解决GPU显存不足的限制, 但另一方面引入了通信量的问题。在新一代的GPU架构中(Fermi架构)增加了GPU-DMA技术, 该技术可以直接读取和写入CUDA主机内存, 消除不必要的系统内存拷贝和CPU开销, 还支持GPU之间以及类似NUMA结构的GPU到其他GPU内存的直接访问的P2P的DMA直接传输。NVIDIA2013年初推出的CUDA5.0可实现GPU-RDMA技术(仅支持Infiniband网络连接 5 GB/s的速度)。利用这一技术, 可以减少GPU与CPU之间的数据通信, 提高通信效率。另一方面, 利用多卡联合计算一炮数据, 意味着将一个炮数据体分别用不同的GPU卡计算, 那么在计算过程中就需要卡与卡之间的数据交换, 从而增加了GPU卡之间的I/O通信量。为了优化GPU卡间的数据通信, 采用数据I/O隐藏策略, 将数据体按照GPU显存进行划分, 每块卡上的数据又可分为独立计算部分和边界的重叠计算部分。计算过程分为两步进行, 如图3所示:①首先对重叠数据部分B区块进行计算; ②在计算独立数据部分A的同时, 进行重叠数据B的交换。计算A数据时从远离B的一端开始, 由于A区块远大于B区块, 这样可保证计算到B时是新交换的数据。这样即实现了数据通信的隐藏, 提高了效率。

	Figure Option View Download New Window
	图3 区域分解数据交换

1.4 多线程流计算与并行传输技术

实现数据I/O隐藏必须利用GPU流处理技术。GPU计算中可以创建多个流, 由于每个流须按一定的顺序执行一系列操作, 而对于不同的流之间可以并行执行, 也可以乱序执行。这样, 可以使一个流的计算与另一个流的数据传输并行执行, 可有效地提高GPU中资源利用率。

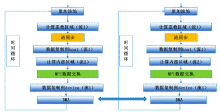
流的定义方法:首先创建一个流cudaStream_t对象, 并在启动内核和内存与显存进行数据拷贝memcpy时将该对象作为参数传入GPU显存, 参数相同的属于同一个流, 参数不同的属于不同的流。具体计算流程如图4。

	Figure Option View Download New Window
	图4 基于流的多卡GPU-RTM实现策略

从以上实现过程可以看出, 在实现多卡GPU-RTM技术中不仅要考虑GPU卡之间的数据交换, 还要利用GPU流技术来实现计算与传输的并行, 掌握好不同计算流之间的同步与异步执行, 实现过程相对来说比较复杂。但是这种基于流的GPU-RTM技术解决了GPU显存不足的瓶颈, 可以实现任意大生产规模的RTM数据处理。

1.5 效率测试

1.5.1 只考虑通信, 关闭计算模块

以某区的实际计算规模为依据, 构造波场数据, 然后仅进行通信效率的测试, 关闭计算函数, 统计通信时间。分别比较MPI方式、MPI+GPU-DMA方式和GPU-RDMA方式所消耗的通信时间。如表1 所示, 基于MPI通信的效率最低, MPI+DMA方式通信效率提高了1倍, 加入RDMA方式通信效率又提高了1倍左右。

表1 通信性能对比

1.5.2 同时考虑通信与计算

同时打开通信与计算模块, 仍然运行某区的实际资料。计算通信数据量与GPU波场吞吐量, 分别

估计消耗的时间, 然后与实际运行的总体时间比较, 若总时间与计算时间相当, 表明通信时间被隐藏; 若总时间与计算时间相差很大, 则表明通信和计算并未实现隐藏。

如表2所示, MPI通信时间和计算时间是串行完成, GPU-DMA技术提高了通信效率但是仍然为串行完成, RDMA+Stream方式总计算时间与纯计算时间相当。多线程流计算与并行传输技术实现了通信时间隐藏, 总体运行效率提高9%左右。

表2 总体性能比较

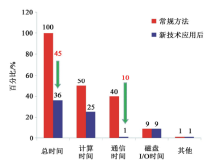
如图5所示, 采用GPU-DMA和GPU-Stream技术优化升级RTM的并行结构后, 通信时间几乎完全被消除, 仅剩1%的时间比重。这项技术在解决通信问题的同时, 总体运行效率提高了39%左右。

	Figure Option View Download New Window
	图5 总体性能与单项性能统计

2 叠前逆时偏移技术生产应用

随着开发难度不断加大, 对于缝洞型储层预测的精度要求越来越高。因此, 必须提高地震资料的分辨率和信噪比, 提高资料对小规模缝洞体、微幅构造的识别能力, 提升地震资料品质, 提高储层预测精度, 以满足油田高效开发工作的需求。在某区部署满叠面积为151 km²的高精度三维地震勘探, 地震资料采集观测系统采用可变面元, 覆盖次数高, 偏移距大, 方位角宽, 适合做观测系统的退化研究。观测系统:32线× 34炮× 374道; 面元尺寸:15 m × 15 m, 7.5 m× 7.5 m; 覆盖次数:22× 16=352次, 11× 8 =88次; 总炮数:36 550炮; 炮密度:242炮/km²; 叠前数据量12.5 TB。

RTM同时采用全声波方程进行震源和检波点波场延拓, 汇集了Kirchhoff方法和单程波动方程方法的优点于一身, 它克服了偏移倾角和偏移孔径的限制, 可以有效地处理纵横向存在剧烈变化的地球介质物性特征。该技术具有相位准确、成像精度高、对介质横向速度变化和高陡倾角适应性强、甚至可以利用回转波、多次波正确成像等优点, 特别是RTM成像技术在提高地震资料信噪比、提高复杂构造的成像精度、突出岩性等方面具有优势。

图6为Kirchhoff叠前深度偏移与逆时偏移的对比剖面。从对比结果可清楚地看到, 逆时偏移的“ 串珠” 成像聚焦更好且能量更强, 剖面的背景噪声也小, 奥陶系里的弱层反射在一定程度上得到了改善。

	Figure Option View Download New Window
	图6 偏移方法测试

3 计算效率统计

采用7.5 m× 7.5 m的成像面元, 10 km× 8 km的成像孔径, 使用202个CPU节点共3 232核计算部分炮时间, 然后估算总体运行时间为293天, 总用机时56 560天。若改用GPU平台66个节点, 132GPU卡, 仅需21天即可完成, 共用GPU集群机时1 412天, 整体效率提升40倍左右(表3)。

表3 某区RTM计算效率对比

4 结论

基于GPU的叠前逆时深度偏移处理海量地震数据时的实用性, 是复杂探区油气勘探不可回避的问题。基于GPU-RDMA直接通信技术和GPU-Stream流技术的并行算法, 适合于GPU集群的大规模分布式并行计算, 可显著提高海量数据RTM计算效率。应用高密度地震数据测试结果可见, 文中介绍的GPU-RTM具有成像精度高、并行计算稳定性好、计算速度快等特点。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Whitemore N D. Iterative depth migration by backward time propagation[C]//Expand ed Abstracts of 53^rd SEG Annual Internet Meeting, 1983: 382-385. [本文引用:1]
[2]	Symes W W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 72(5): SM213-SM221. [本文引用:1]
[3]	Clapp R G. Reverse-time migration with rand om boundaries[C]//Expand ed Abstracts of 79^th SEG Annual Internet Meeting, 2009: 2809-2813. [本文引用:1]
[4]	Feng B, Wang H Z, et al. A strategy for source wavefield reconstruction in reverse time migration[C]//Expand ed Abstracts of 81^st SEG Annual Internet Meeting, 2011: 3164-3168. [本文引用:1]
[5]	NVIDIA. Tesla GPU computing technical brief , Ver2sion1. 0. 0[EB/ OL]. [本文引用:1]
[6]	Micikevicius P. 3D finite difference computation on GPUs using CUDA[C]//Expand ed Abstracts of 78^th SEG Annual Internet Meeting, 2008: 79-84. [本文引用:1]
[7]	Foltinek D, et al. Industial-scale reverse time migration on GPU hardware[C]//Expand ed Abstracts of 79^th SEG Annual Internet Meeting, 2009: 2789-2793. [本文引用:1]
[8]	赵改善. 地球物理高性能计算的新选择: GPU 计算技术[J]. 勘探地球物理进展, 2007, 30(5): 399-404. [本文引用:1]
[9]	张兵, 赵改善, 黄骏, 等. 地震叠前深度偏移在CUDA平台上的实现[J]. 勘探地球物理进展, 2008, 31(6): 427-432. [本文引用:1]
[10]	李肯立, 彭俊杰, 周仕勇. 基于CUDA的Kirchhoff叠前时间偏移算法设计与实现[J]. 计算机应用研究, 2009, 26(12): 4774-4777. [本文引用:1]
[11]	刘红伟, 李博, 刘洪. 地震叠前逆时偏移高阶有限差分算法及GPU 实现[J]. 地球物理学报, 2010, 53(7): 1725-1733. [本文引用:1]
[12]	赵磊, 王华忠, 刘守伟. 逆时深度偏移成像方法及其在CPU/GPU异构平台上的实现[J]. 岩性油气藏, 2010, 22(7): 36-41. [本文引用:1]
[13]	李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策[J]. 地球物理学报, 2010, 53(12): 2938-2943. [本文引用:1]
[14]	刘守伟, 王华忠, 陈生昌, 等. 三维逆时偏移GPU/CPU机群实现方案研究[J]. 地球物理学报, 2013, 56(10): 3487-3496. [本文引用:1]
[15]	Dablain M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. [本文引用:1]

1983

0.0

... 基于全声波方程的逆时叠前深度偏移(pre-stack reverse-time depth migration,RTM)^[1]是具有明确地质意义的精确成像方法 ...

2007

0.0

... Symes^[2]提出CheckPointing方法,在增加一定计算量的基础上减少波场的存储需求 ...

2009

0.0

... Robert^[3]提出用随机边界条件代替吸收边界条件,通过增加一次波场反传重建波场的方式来实现相关成像条件,可以完全消除波场存储问题,但在实际应用过程中,随机边界条件通常在剖面中带来一些随机干扰,影响成像质量 ...

2011

0.0

... Feng^[4]提出一种新的波场重构策略,通过成像体四周波场反传来重构整个成像空间的波场,利用该策略实现逆时偏移,边界条件仍然使用常规的吸收边界,计算量、存储量以及成像效果均基本满足要求 ...

0.0

... 当前高性能领域最流行的加速器GPU(graphic processing unit),以其强大的计算性能,不断改善的编程界面吸引了来自众多非图形计算领域的关注,是一种极具发展潜力的处理器体系结构^[5] ...

2008

0.0

... 如Micikevicius等^[6]研究了基于CUDA平台的有限差分实现问题,给出了快速实现有限差分的算法 ...

2009

0.0

... Foltinek等^[7]讨论了生产规模数据的逆时偏移在GPU上实现的挑战,讨论了区域分解进行的必要性 ...

2007

0.0

... 国内研究人员也对GPU在地球物理上的应用进行了大量研究,早在2007年,赵改善^[8]就提出了将GPU应用于地球物理计算中 ...

2008

0.0

... 2008年,张兵等^[9]实现了基于CUDA的二维叠前深度偏移技术 ...

2009

0.0

... 李肯立等^[10]实现了基于CUDA的叠前时间偏移技术 ...

2010

0.0

... 在逆时偏移方面,刘红伟等^[11]进行了二维高阶差分GPU逆时偏移 ...

2010

0.0

... 赵磊等^[12]进行了三维逆时偏移的GPU实现 ...

2010

0.0

... 李博等^[13]对比分析了基于CPU/GPU平台的逆时偏移实现策略 ...

2013

0.0

... 刘守伟等^[14]比较系统地阐述了GPU逆时偏移的相关问题 ...

1986

0.0

... Dablain于1986年^[15]提出利用高阶差分方程来进行上述模拟和偏移过程 ...