负视速度超前预报倾斜界面位置确定

引用本文

侯伟, 杨正华. 负视速度超前预报倾斜界面位置确定[J]. 物探与化探, 2015,39(5): 1089-1093.
HOU Wei, YANG Zheng-Hua. The determination of the position of tilted interface matching in negative apparent velocity tunnel seismic prediction[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1089-1093.
Doi:10.11720/wtyht.2015.5.35 复制到剪切板

Permissions

《物探与化探》编辑部

负视速度超前预报倾斜界面位置确定

侯伟, 杨正华

长安大学地质工程与测绘学院地球物理系,陕西西安 710054

杨正华(1957-) ,男,教授,长安大学地球物理研究所,主要从事矿物岩石和地球物理有关方面的研究工作。

作者简介: 侯伟(1989-) ,男,硕士研究生,主要从事地震勘探和隧道超前地质预报方面的研究工作。

收稿日期: 2014-11-30

摘要

在隧道超前地质预报中,负视速度法以其简便、快速的特点被广泛应用。常规的方法是直达波时距曲线和反射波时距曲线的交点即为反射界面的位置;但是对于倾斜界面,如果只是单纯的延伸时距曲线,并不能准确地找出界面位置,而且当倾斜角度比较大时,误差更大,这样在实际处理数据时,往往因为处理不当,造成预报的不准确,以致于实际操作出现大的事故。针对此问题,笔者主要研究倾斜界面,采用最新坐标法求反射界面的时距曲线,并对所得时距曲线进行插值拟合,主要包括多项式拟合、一元三点等距插值以及连分式插值。通过大量试验,比较各个插值拟合的特点,最终得出由多项式拟合对时距曲线插值,能够准确地确定反射界面的位置;最后通过几何公式求出界面倾角(视倾角),为负视速度法数据处理提供方便。

关键词: 隧道; 超前预报; 负视速度; 倾斜界面; 插值拟合

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)05-1089-05 doi: 10.11720/wtyht.2015.5.35

The determination of the position of tilted interface matching in negative apparent velocity tunnel seismic prediction

HOU Wei, YANG Zheng-Hua

The Geophysical Department of School of Geological Engineering and Geomatics,Chang'an University,Xi'an 710054,China

Abstract

With the merits of simplicity and rapidness, the negative apparent velocity method has been used widely in tunnel geological prediction. The regular method indicates that the intersection of time-distance curves of direct wave and reflected wave is just the position of reflecting interface. However, for inclined interface, the interface position cannot be identified accurately if we only extend time-distance curves. What's more, the more lean the angle, the greater the error. This leads to serious accidents in practice because of inaccurate prediction. Aimed at solving the problem, the authors mainly studied the inclined interface, used the newest coordinates method to get time-distance curve of reflected interface, and then fitted their interpolation, mainly including polynomial fitting curve, unitary three-points isometric interpolation and interpolation by continued fractions. Through a lot of tests and comparisons of the characteristics of all interpolation fittings, the time distance curve interpolation by polynomial fitting can be worked out so as to identify the position of reflected interface accurately. Finally, interface dip (apparent dip) can be calculated using geometric formula. This method facilitates the data processing by means of negative apparent velocity.

Keyword: tunnel; forecast; negative apparent velocity; tilted interface; interpolation

Show Figures

负视速度法是我国较早开展的隧道地震反射超前预报方法, 国内将这种方法称为负视速度法, 国外称其为隧道VSP技术。它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中, 利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^{[1, 2, 3, 4, 5]}。在激震点进行激发, 产生的地震波信号会在隧道周围岩体内传播, 当地质体与围岩存在弹性差异时, 入射波便会在弹性界面处发生反射、折射与透射现象, 在界面的不连续处还会产生衍射波^{[6, 7]}。在隧道侧壁布置一条测线, 当测线方向与前方反射界面呈直立正交时, 所接收到的反射波与直达波相比呈负视速度形状, 其延长线与直达波延长线的交点即为反射界面的位置; 但是当界面倾斜时, 如果按照原来的方法顺势延伸, 就会存在许多问题, 当界面倾斜比较大时, 就需要对所观测到的数据进行处理(插值拟合)^{[6, 8, 9]}。针对这一问题, 笔者通过大量的实验, 比较各种插值方法的优缺点, 包括最小二乘法多项式拟合、一元三点等距插值、连分式插值、三次样条插值等等, 发现多项式最小二乘法多项式拟合在处理此问题时有很大的好处, 可以较为准确地确定倾斜界面的位置。

1 建立数值计算方程

模拟实验, 采用24炮激发, 单道接收(可以通过改变接收点的横坐标来得到其他点), 炮间距为2 m, 偏移距为10 m。

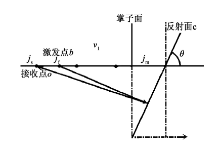
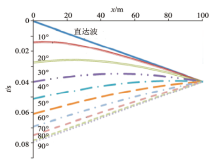
	Figure Option View Download New Window
	图1 倾斜反射界面模型

(单一垂直界面模型如图1所示。设地震波的视速度为v₁ , 接收点至o点的距离为j_s(本实验接收点设为o点), 激发点至o点的距离为j_f, 反射界面至o点的距离为j_m, θ 为隧道轴线与反射界面的夹角。由于是垂直界面, 通过改变j_m, 来观察时距曲线的特点^[10]。

对于单一界面j_m为倾斜时, 根据虚震源原理可以推导出倾斜界面反射波时距曲线方程^[11]

$\begin{matrix} t = \frac{\sqrt{[2(j_{m} cosθ - j_{f} sinθ) cosθ - j_{s}]^{2} + [2 (j_{m} cosθ - j_{f}) sinθ + j_{f}]^{2}}}{v_{1}} (1) \end{matrix}$

对于多层界面, 可以运用坐标法来求反射波时距曲线方程。设震源和接收点坐标分别为(x₀, y₀)和(x_n, y_n), 各层的界面方程为

$\begin{matrix} y = k_{i} + b_{i}, i = 0, 1, \dots, n 。 (2) \end{matrix}$

求震源到接收点的时距曲线, 具体算法如下:

$\begin{matrix} t = \frac{\overset{n}{\sum_{i = 1}} \sqrt{(x_{i} - x_{i - 1})^{2} + (y_{i} - y_{i - 1})^{2}}}{v_{1}}, (3) \end{matrix}$

根据最小走时原理, 有

$\begin{matrix} \frac{\partial t}{\partial x_{i}} = 0, i = 1, 2, \dots, n - 1 。 (4) \end{matrix}$

令

$\begin{matrix} f (x_{1}, x_{2}, \dots, x_{n - 1}) = \frac{\partial t}{\partial x_{i}}, i = 1, 2, \dots, n - 1, (5) \end{matrix}$

问题就转化为代数问题及求解该非线性方程组的解x₁, x₂, …, x_n_-1, 然后通过已知的界面线性方程求得界面上交点的坐标, 就可以很方便地求出反射波时距曲线^[1]。

2 倾斜界面插值拟合分析

下面主要展示通过最小二乘法多项式拟合、一元三点等距插值和连分式插值这三种方法处理所得到的时距曲线。

	Figure Option View Download New Window
	图2 倾斜界面视倾角10° 的反射波多项式拟合曲线

2.1 最小二乘法多项式插值拟合

假设地震记录(x_i, y_i)(i=0, 1, ..., m), φ 为所有次数不超过n(n≤ m)的多项式构成的函数类。先求 $\begin{matrix} \begin{matrix} p_{n} (x) = \overset{n}{\sum_{k = 0}} a_{k} x^{k} \in φ, \end{matrix} \end{matrix}$

使得

$\begin{matrix} I = \overset{M}{\sum_{i = 0}} [p_{n} (x) - y_{i}]^{2} = \overset{M}{\sum_{i = 1}} {(\overset{n}{\sum_{k}} a_{k} x^{k} - y_{i})}^{2} = \min, (6) \end{matrix}$

显然, $\begin{matrix} t = \overset{M}{\sum_{i = 0}} [p_{n} (x) - y_{i}]^{2} = \overset{M}{\sum_{i = 1}} {(\overset{n}{\sum_{k}} a_{k} x^{k} - y_{i})}^{2} \end{matrix}$ 为a₀, a₁, …, a_n的多元函数, 因此上述问题即为求I=

I(a₀, a₁, …, a_n)的极值问题, 有多元函数求极值的必要条件, 得

$\begin{matrix} \frac{\partial I}{\partial a_{j}} = 2 \overset{M}{\sum_{i = 0}} (\overset{n}{\sum_{k = 0}} a_{k} x^{k} - y_{i}) x_{i}^{j} = 0, j = 0, 1, \dots, n, (7) \end{matrix}$

即

$\begin{matrix} \overset{n}{\sum_{k = 0}} (\overset{m}{\sum_{i = 0}} x_{i}^{j + k}) a_{k} = \overset{m}{\sum_{i = 0}} x_{i}^{j} y_{i}, j = 0, 1, \dots, n 。 (8) \end{matrix}$

上式是关于a₀, a₁, …, a_n的线性方程组, 用举证表示为

$\begin{matrix} [\begin{matrix} m + 1 & \overset{m}{\sum_{i = 0}} x_{i} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{n} \\ \overset{m}{\sum_{i = 0}} x_{i} & \overset{m}{\sum_{i = 0}} x_{i}^{2} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{n + 1} \\ ︙ & ︙ & ︙ & ︙ \\ \overset{m}{\sum_{i = 0}} x_{i}^{n} & \overset{m}{\sum_{i = 0}} x_{i}^{n + 1} & \dots & \overset{m}{\sum_{i = 0}} x_{i}^{2 n} \end{matrix}] [\begin{matrix} a_{0} \\ a_{1} \\ ︙ \\ a_{n} \end{matrix}] = [\begin{matrix} \overset{m}{\sum_{i = 0}} y_{i} \\ \overset{m}{\sum_{i = 0}} x_{i} y_{i} \\ ︙ \\ \overset{m}{\sum_{i = 0}} x_{i}^{n} y_{i} \end{matrix}] 。 (9) \end{matrix}$

可以证明上述方程组的系数矩阵是一个对称正定矩阵, 故存在唯一解, 从上式可以解出a_k(k=0, 1, …, n), 从而得出多项式^{[1, 12, 13, 14]}

$\begin{matrix} p_{n} (x) = \overset{n}{\sum_{k = 0}} a_{k} x^{k} 。 (10) \end{matrix}$

把倾斜界面倾角分为小角度(0° ~30° )和大角度(30° ~90° ), 首先通过公式法求取掌子面之前的时距曲线数据, 接下来采用多项式拟合的整体插值和分段插值来处理数据曲线, 并且与数值计算的时距曲线所确定的界面位置进行对比^[2]。

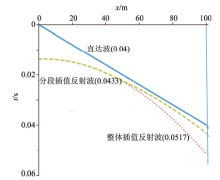
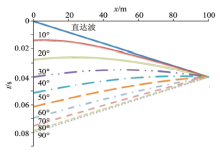
	Figure Option View Download New Window
	图3 倾斜界面视倾角20° 的反射波多项式拟合曲线

图2和图3说明, 倾斜界面倾角为10° 和20° 时, 多项式拟合整体插值和分段插值所得反射波时距曲线的特点可以很明显地看出, 分段插值在小角度倾角时可以准确确定界面位置, 为处理小角度倾斜界面带来帮助(曲线上标注的数据为拟合差值, 下同)。

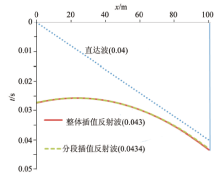
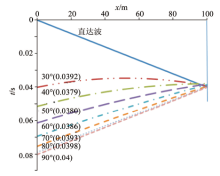
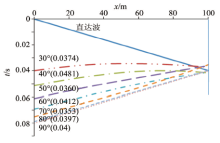
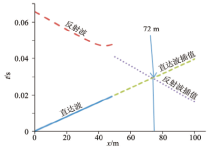
	Figure Option View Download New Window
	图4 倾斜界面视倾角30° ~90° 的反射波多项式拟合曲线

图4和图5图中分别展示了倾角在30° ~90° 之间数值计算和多项式拟合得到的反射波时距曲线, 可以看出在此范围内, 多项式拟合所得的反射波时距曲线和数值计算得到的基本吻合。

	Figure Option View Download New Window
	图5 倾斜界面视倾角10° ~90° 的反射波数值计算时距曲线

2.2 一元三点插值拟合

下面对倾斜界面时距曲线进行一元三点等距插值, 确定反射界面位置, 并与数值计算所确定的界面进行对比。

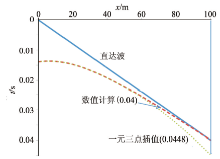
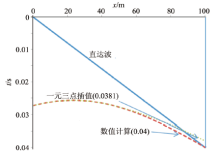
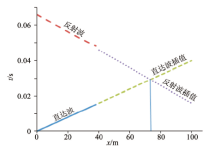
	Figure Option View Download New Window
	图6 倾斜界面视倾角10° 的一元三点等距插值时距曲线

图6和图7是把倾斜界面视倾角为10° 和20° 的数值计算结果和一元三点等距插值所得的时距曲线进行对比, 可以看出两者之间存在着一定的误差, 但是在20° 时, 误差很小, 故继续增大角度。

	Figure Option View Download New Window
	图7 倾斜界面视倾角20° 的一元三点等距插值时距曲线

对比图8和图9可以看出, 一元三点等距插值所得的时距曲线误差很小, 但是对比图5和图8, 发现图5的误差更小, 这也从中体现出多项式拟合对于界面位置确定的准确性。

	Figure Option View Download New Window
	图8 倾斜界面视倾角30° ~90° 的一元三点等距插值时距曲线

	Figure Option View Download New Window
	图9 倾斜界面视倾角10° ~90° 的数值计算时距曲线

2.3 连分式插值拟合(三层倾斜界面)

通过坐标法求取三层倾斜界面第三层的时距曲线, 用连分式和改进连分式进行插值。连分式插值具有快速拟合和逼近的特点, 从图10和图11中可以看出, 小范围的数据变化不能影响整体数据的变化趋势, 在处理数据时, 如果发现小范围内有数据异常或者错误, 可以通过连分式插值求取反射波和直达波时距曲线, 这样得到的反射界面位置相对比较准确。

	Figure Option View Download New Window
	图10 连分式插值时距曲线

	Figure Option View Download New Window
	图11 连分式插值改进后的时距曲线

	Figure Option View Download New Window
	图12 两点法求视倾角示意

3 倾斜反射界面角度的确定

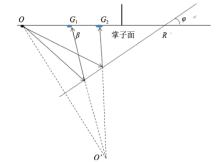
通过插值模拟, 确定了反射界面的大体位置, 但是倾角并不知道。如图12所示, 设O为震源位置, G₁、G₂为接收点, O'相当于震源O反射界面的镜像点。设t₁为G₁点的初至时间, t₂为G₂点的初至时间, t₃为G₁点的双程反射时间, t₄为G₂点的双程反射时间, t₅为OO'的旅行时间^{[3, 8, 13, 14, 15, 16, 17, 18, 19]}。根据几何关系和余弦定理可以推导出公式

$\begin{matrix} \begin{matrix} cosβ = [t_{3}^{2} + (t_{1} - t_{2})^{2} - t_{4}^{2}] / [2 t_{3} (t_{1} - t_{2})], (11) \\ t_{5}^{2} = t_{1}^{2} + t_{3}^{2} - 2 t_{1} t_{3} cosβ, (12) \\ cosφ = t_{3} sinβ / t_{5} 。 (13) \end{matrix} \end{matrix}$

这样可以求出反射界面与隧道的夹角, 即倾角, 如在倾角取30° 、60° 、80° 时, 求出的角度为30.15° 、63.91° 、84.5° , 误差分别为0.5%、6.5%、5.6%, 可以说比较准确。

4 结论与局限

笔者主要针对倾斜界面反射波和直达波时距曲线进行讨论, 为准确确定倾斜界面位置, 先采用多种插值拟合方法处理时距曲线, 总体来说分为大角度(30° ~90° )和小角度(0° ~30° ), 并分别比较各个插值方法的优缺点, 再通过公式确定倾斜界面的倾角, 得出结论:

(1)对于小角度, 多项式分段拟合具有较小的误差, 在处理数据时, 当界面倾角较小时, 可以采用分段多项式拟合, 这样可以较准确地找出界面位置。

(2)对于大角度, 多项式拟合和一元三点等距插值误差基本一样, 但相对来说多项式拟合误差较小。连分时插值在进行小角度处理时效果不太好。

(3)通过连分式插值对三层倾斜界面第三层界面的时距曲线进行插值, 并将改进后和改进前进行了比较, 基本可以确定倾斜界面位置(笔者对两层界面的验证效果还可以, 故在此给出第三层倾斜界面的处理结果)。

(4)对倾斜界面的角度(视倾角)求法进行了细致的公式说明, 视倾角和界面距离即可以决定倾斜界面的大体位置。由于是在二维坐标下求取的, 所用倾角为视倾角, 对于倾向无法确定。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	程乾生. 数字信号处理[M]. 北京: 北京大学出版社, 2008. [本文引用:3]
[2]	杨耀. 地震视负速度法在隧道超前地质预报中的应用[J]. 工程地球物理学报, 2009, 6(6): 754-758. [本文引用:2]
[3]	曾昭璜. 隧道地震反射法超前预报[J]. 地球物理学报, 1994, 37(2): 218-230. [本文引用:2]
[4]	赵永贵. 中国工程地球物理研究的进展与未来[J]. 地球物理学进展, 2002, 17(2): 301-304. [本文引用:1]
[5]	刘秀峰, 李忠. TSP探测数据采集和处理中应注意的问题[J]. 石家庄铁道学院学报, 2002, 15(2): 56-59. [本文引用:1]
[6]	Liu X W, Liu H, Li Y M. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics (in Chinese), 2004, 19(1): 8-11. [本文引用:2]
[7]	Eaton D W, Clarke G. A Kirchhoff integral method tomodel 3-D elastic-wave scattering[C]//Expand ed Ab-stracts of 70thAnnual International SEG Meeting, 2000, 1-4. [本文引用:1]
[8]	何振起, 李海, 梁彦忠. 利用地震反射法进行隧道施工地质超前预报[J]. 铁道工程学报, 2000;4: 81-85. [本文引用:2]
[9]	张景科, 谌文武, 雷启云. TSP203地质超前预报原理及其提高精度的途径[J]. 西部探矿工程, 2005, 17(7): 101-103. [本文引用:1]
[10]	Einar M. Sampling, aliasing, and inverting the linear Radon transform[J]. geophysics, 2004, 69(3): 859-861. [本文引用:1]
[11]	Kennet P, Ireson R L. The VSP as an interpretation toll for structural and stratigraphic Analysis[C]//SEG 1st Annual Meeting, 1981. [本文引用:1]
[12]	朱光明. 数字信号分析与处理[M]. 西安: 陕西人民教育出版社, 2003. [本文引用:1]
[13]	李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008. [本文引用:2]
[14]	程乾生. 信号数字处理的数学原理[M]. 北京: 石油工业出版社, 1979. [本文引用:2]
[15]	蔡运胜. TSP203 型隧道超前地质预报系统及应用[J]. 物探与化探, 2004, 28(2): 184-186. [本文引用:1]
[16]	郭有劲. 综合物探方法在隧道超前预报中的应用研究[D]. 北京: 中国地质大学, 2010. [本文引用:1]
[17]	刘云祯. TGP隧道地震波预报系统与技术[J]. 物探与化探, 2009, 33(2): 170-177. [本文引用:1]
[18]	舒森. 如何提高TSP203系统在应用中的准确性[J]. 物探与化探, 2011, 35(5): 1710-714. [本文引用:1]
[19]	王晓川, 康勇, 夏彬伟. 对提高TGP隧道地质预报系统准确性的分析[J]. 物探与化探, 2012, 36(1): 153-158. [本文引用:1]

2008

0.0

... 它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中,利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^[1,2,3,4,5] ...

... 问题就转化为代数问题及求解该非线性方程组的解x₁,x₂,…,x_n_-1,然后通过已知的界面线性方程求得界面上交点的坐标,就可以很方便地求出反射波时距曲线^[1] ...

... 可以证明上述方程组的系数矩阵是一个对称正定矩阵,故存在唯一解,从上式可以解出a_k(k=0,1,…,n),从而得出多项式^[1,12,13,14] ...

2009

0.0

杨耀. 地震视负速度法在隧道超前地质预报中的应用[J]. 工程地球物理学报, 2009, 6(6): 754-758.

地震视负速度法是一种快速、有效、经济的物探法超前地质预报技术,其本质是利用物性差异来解决地质问题的一种勘查方法.本文阐述了地震视负速度法技术,结合实例介绍了该方法在探明隧道掌子面前方一定距离内的地质情况的应用中所取得的实际效果,并提出了在实际应用中部分需要注意的问题.说明采用地震视负速度法从事隧道超前地质预报是一种行之有效的方法.

... 它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中,利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^[1,2,3,4,5] ...

... ),首先通过公式法求取掌子面之前的时距曲线数据,接下来采用多项式拟合的整体插值和分段插值来处理数据曲线,并且与数值计算的时距曲线所确定的界面位置进行对比^[2] ...

1994

0.0

曾昭璜. 隧道地震反射法超前预报[J]. 地球物理学报, 1994, 37(2): 218-230.

In the article, negative apparent velocity event which tunnel vertical seismic profiling has got is used to resolve the sign of the reflected wave from the front of the tunnel face. Then this sign is used to invert space position and strike and dip of reflecter in order to get predictino.

利用隧道垂直地震剖面所得到的负视速度同相轴，用此作为识别来自隧道施工掌子面前方界面的反射波标志．然后利用这一标志推演出反射界面的空间位置与产状，达到超前预报的目的．

... 它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中,利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^[1,2,3,4,5] ...

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2002

0.0

赵永贵. 中国工程地球物理研究的进展与未来[J]. 地球物理学进展, 2002, 17(2): 301-304.

Since the beginning of 90 years last century, begining at 90s of last centary engineering geophysics has developed more tuan 10 years now. Howevev it is still at its primary stage of development. Its equipment and technique are undergoing a great change from depending on import to independent development. In last few years, the studies of new technique and instruments have a great progress and some kinds of instruments are as good as invport prodacts in their function and technology. However, in engineering geophysics filed there are many problems: such as technique study, software and instrument development. It is an urgent matter of the profession to strengthen cooperation, to organize technique study and software development and to promote instrument factory combined. In the predictable 5 years, engineering geophysics technique and its application well have a good future. Engineering ge

中国工程地球物理从上世纪90年代初期开始,经历了近十年的发展历程,现还处于初期阶段.所使用的方法和仪器正处于由完全依赖进口向自主开发的转变之中.近几年来新方法研究和仪器自主开发取得了很大进展,不少仪器性能可以与国外相媲美,展现了良好的发展势头.目前工程地球物理研究还存在着方法局限、软件开发滞缓、仪器开发分散的被动局面.加强行业合作,促进方法研究和软件开发,推动仪器厂商联合是行业发展的当务之急.可以预见未来的五年是工程地球物理技术发展与应用的黄金时代.

... 它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中,利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^[1,2,3,4,5] ...

2002

0.0

刘秀峰, 李忠. TSP探测数据采集和处理中应注意的问题[J]. 石家庄铁道学院学报, 2002, 15(2): 56-59.

从TSP超前地质预报系统的工作原理出发,详细阐明各部件的工作本质,论述了数据处理每一步操作的目的,提出了在实际操作时应注意的问题,使TSP探测中数据的采集和处理等各项操作能有的放矢.

... 它将地面地震勘探中VSP法原理应用于近水平的隧洞超前探测中,利用地震反射波信号特征来分析预报隧洞开挖面前方围岩的地质情况^[1,2,3,4,5] ...

2004

0.0

... 在激震点进行激发,产生的地震波信号会在隧道周围岩体内传播,当地质体与围岩存在弹性差异时,入射波便会在弹性界面处发生反射、折射与透射现象,在界面的不连续处还会产生衍射波^[6,7] ...

... 但是当界面倾斜时,如果按照原来的方法顺势延伸,就会存在许多问题,当界面倾斜比较大时,就需要对所观测到的数据进行处理(插值拟合)^[6,8,9] ...

2000

0.0

2000

0.0

何振起, 李海, 梁彦忠. 利用地震反射法进行隧道施工地质超前预报[J]. 铁道工程学报, 2000;4: 81-85.

本文介绍了两种利用物探技术进行地质超前预报的方法,即地震负视速度法(测试面与被探测面互为垂直的观测系统)及地震横排列法(震源孔和接收孔分别位于掌子面两侧的侧壁上,有规律地横向排列)的原理及测试方法,文中还介绍了两个工程实例.

... 但是当界面倾斜时,如果按照原来的方法顺势延伸,就会存在许多问题,当界面倾斜比较大时,就需要对所观测到的数据进行处理(插值拟合)^[6,8,9] ...

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2005

0.0

张景科, 谌文武, 雷启云. TSP203地质超前预报原理及其提高精度的途径[J]. 西部探矿工程, 2005, 17(7): 101-103.

TSP203是目前世界上最先进的隧道地质超前预报系统,笔者介绍了该系统的探测原理和提高探测精度的途径,并对进一步提高精度的途径进行了讨论.

... 但是当界面倾斜时,如果按照原来的方法顺势延伸,就会存在许多问题,当界面倾斜比较大时,就需要对所观测到的数据进行处理(插值拟合)^[6,8,9] ...

2004

0.0

... 由于是垂直界面,通过改变j_m,来观察时距曲线的特点^[10] ...

1981

0.0

... 对于单一界面j_m为倾斜时,根据虚震源原理可以推导出倾斜界面反射波时距曲线方程^[11] ...

2003

0.0

... 可以证明上述方程组的系数矩阵是一个对称正定矩阵,故存在唯一解,从上式可以解出a_k(k=0,1,…,n),从而得出多项式^[1,12,13,14] ...

2008

0.0

... 可以证明上述方程组的系数矩阵是一个对称正定矩阵,故存在唯一解,从上式可以解出a_k(k=0,1,…,n),从而得出多项式^[1,12,13,14] ...

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

1979

0.0

... 可以证明上述方程组的系数矩阵是一个对称正定矩阵,故存在唯一解,从上式可以解出a_k(k=0,1,…,n),从而得出多项式^[1,12,13,14] ...

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2004

0.0

蔡运胜. TSP203 型隧道超前地质预报系统及应用[J]. 物探与化探, 2004, 28(2): 184-186.

This paper deals with the TSP203 type tunnel wall rock geological forecast system, describing its constituents, functions, working principle and method, and the steps of data processing. Examples are given to illustrate its application results.

介绍了TSP203型超前地质预报系统的组成、性能以及工作原理与方法,数据处理的步骤,通过工程实例分析说明其应用效果。

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2010

0.0

郭有劲. 综合物探方法在隧道超前预报中的应用研究[D]. 北京: 中国地质大学, 2010.

综合物探超前地质预报是确保隧道施工安全的必不可少的一种方法,从上世纪90年代初期开始,经历了十几年的发展,现正逐渐走向成熟。虽然方法本身在发展中存在许多问题,但在专家和学者的努力下逐渐得到了克服。综合物探超前地质预报方法和所使用的仪器正由完全依赖进口向自主开发转变中,方法种类繁多,展现了良好的发展势头。目前应用最多,也最受推崇的主要有TSP超前地质预报系统、探地雷达法和红外探水法,尤其是三者的有效组合。实际工作中,TSP方法主要用于长距离预报,探地雷达方法为短距离定量精确预报,红外探水法则主要对隧道掌子面前方有无含水做定性评价。这三种方法若能合理组合,可以互相佐证,提高预报结果的准确性。本文分别阐述了TSP超前地质预报系统、探地雷达法和红外探水法的基本原理,以及这三种方法常用的仪器设备类型,并以三种方法在武广铁路客运专线坪岭隧道施工超前地质预报的综合应用上加以阐述综合物探方法在隧道超前地质预报的重要性。这是一个难得的综合物探超前地质预报工程应用实例,该隧道所测区段发生了突泥突水,涌泥量达3000多方,但由于超前预报结果的提前预知,从而避免了特大人员伤亡事故的发生,挽回了重大的经济损失。本文详细地介绍各种方法在外业数据采集中测线的布置方法、资料处理程序和采集信号结果的判识原则,并附有对应的信号图像,同时还涉及到数据采集过程中需要注意的事项和改进措施。通过对使用各种方法得出的预报结果对比分析,可以清楚地看到所反映的异常里程位置基本一致,也能清楚地看到综合物探超前地质预报可使施工单位提前采取措施,修正支护参数,从而确保隧道的施工安全,故建议在我国隧道地质超前预报工作中推广应用。但目前超前地质预报依然存在许多问题,比如在排除周围噪声干扰、判断背后空洞体积大小、不良地质体的精确里程位置以及产状分布特征方面等,需要外业操作中设法克服,技术上不断进步加以改进。相信在物探领域内专家学者以及其他相关人士的共同努力下,超前地质预报一定会有质的飞跃和发展。

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2009

0.0

刘云祯. TGP隧道地震波预报系统与技术[J]. 物探与化探, 2009, 33(2): 170-177.

Tunnel engineering is an important component part of such large-scale engineering projects as railway, highway, water conservancy and hydropower constructions. Unclear geological conditions have frequently led to considerable harmfulness caused by tunnel construction accidents. Therefore, the improvement of the advanced geological forecast for tunnel construction is very necessary. The study of tunnel seismic wave advanced forecast technology has been carried out both in China and abroad in the past several years. In this paper, the author has discussed the present situation and existent problems in this aspect, pointed out the deficiency of the TSP technology, dealt with the importance of overcoming blindness and improving scientific forecast, and described the newly-developed TGP tunnel seismic forecast system and its technology as well as its application effects.

隧道工程是铁路、公路和水利水电等大型工程项目中的重要部分，因地质条件不明造成隧道施工事故的危害是巨大的，加强隧道施工地质超前预报工作是非常必要的。国内外对隧道地震波超前预报技术研究已多年，笔者就这方面的现状及及问题进行了讨论，指出了TSP技术存在的不足，阐述了克服盲目性，提高科学预报的重要性，介绍了新开发的TGP隧道地震预报系统与技术及应用效果。

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2011

0.0

舒森. 如何提高TSP203系统在应用中的准确性[J]. 物探与化探, 2011, 35(5): 1710-714.

The transport engineering has massive tunnel construction, and the tunnel construction is likely to be affected by adverse geological structures. In order to reduce the influence of geological disaster on tunnel construction, researchers use the TSP203 geological forecast system to carry out the survey in front of the tunnel face and provide in advance geological prediction that could give instructions for the following construction; nevertheless, due to the existence of much misinformation in the practical application, these means often fail to report the situation or the accurate of the report is too low. These problems often result from the insufficient data acquisition and data processing. Through standard data acquisition and reasonable data processing, the adverse effect might be reduced, and the application accuracy of the TSP203 system in the geological forecast could be improved.

为了减少地质灾害对隧道施工的影响,采用TSP203超前地质预报系统对隧道掌子面前方进行探测,提供超前地质预报,为后续施工提供指导。但是,在实际应用中出现了很多误报、漏报或者准确性太低的情况,这些问题往往是由于数据采集和数据处理中的不足带来的。通过规范的数据采集和合理的数据处理,可以减少这些不足的不良影响,从而提高TSP203系统在超前地质预报应用中的准确性。

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...

2012

0.0

王晓川, 康勇, 夏彬伟. 对提高TGP隧道地质预报系统准确性的分析[J]. 物探与化探, 2012, 36(1): 153-158.

According to the principle of TGP tunnel geological prediction system and the problem existent in the process of detection, this paper has discussed some abnormal-signal-induced factors such as external pulse signal interference, current interference, poor coupling, pipe wave and charging parameters in the data collection, and analyzed the cause of resultant errors with the feedback from engineering application. On such a basis, some suggestions were put forward on improving the understanding of anomalous seismic wave and geological work as well as edge diffraction wave for avoiding the abnormal signal generation and reception. It is concluded that the collection of reliable data is an essential and efficient way to improve the accuracy of TGP system data interpretation.

基于TGP预报系统探测原理及使用过程中存在的问题,指出在数据采集过程中产生异常信号的影响因素为外界脉冲信号干扰、电流干扰、不良耦合、管波干扰及装药质量,结合工程应用的反馈资料分析预报结论产生误差的原因,提出增强对异常地震波的认识、加强地质工作、注意边缘绕射波是根本解决措施,避免产生和接收异常信号,提高采集数据信息的质量,增加TGP预报系统数据信息解释的准确性和可靠性,促进了隧道地质预报技术水平的提高。

... 设t₁为G₁点的初至时间,t₂为G₂点的初至时间,t₃为G₁点的双程反射时间,t₄为G₂点的双程反射时间,t₅为OO'的旅行时间^{[3,8,13,14,15,16,17,18,19]} ...