强衰减条件下<em> Q</em>值修正

引用本文

杨小慧, 陆红梅, 王荣娟, 马媛媛, 袁殿, 崔震, 何元. 强衰减条件下 Q值修正 [J]. 物探与化探, 2015,39(5): 1069-1073.
YANG Xiao-Hui, LU Hong-Mei, WANG Rong-Juan, MA Yuan-Yuan, YUAN Dian, CUI Zhen, HE Yuan. Q modification under the situation of strong attenuation [J]. Geophysical and Geochemical Exploration, 2015,39(5): 1069-1073.
Doi:10.11720/wtyht.2015.5.31 复制到剪切板

Permissions

《物探与化探》编辑部

强衰减条件下 Q值修正

杨小慧¹, 陆红梅², 王荣娟², 马媛媛³, 袁殿³, 崔震³, 何元³

1.中国石化石油物探技术研究院,江苏南京 210014

2.中国石化石油勘探开发研究院,北京 100083

3.中国石油大学(北京) 地球物理与信息学院,北京 102249

作者简介: 杨小慧(1987-),女,江苏如皋人,助理工程师,主要从事地震资料处理方法研究工作。E-mail:yangxiaohui7208@163.com

收稿日期: 2015-02-11

基金: 国家重大专项(2011ZX05024-001-01)

摘要

品质因子( Q)是反映地层对地震波吸收衰减强弱的重要参量。在强衰减条件下,常规方法估算(如谱比法等)的品质因子往往比物理定义的品质因子下限(2π)还小。通过考察两者差异的来源,给出了两者的换算公式。模型测试表明,当品质因数小于30时,常规估算品质因子和物理定义品质因子的相对误差将超过10%,两者应加以区分,不可混用。根据两种品质因子的特点,有如下建议:当拟合 Q-V经验式时,使用物理定义品质因子;当进行反 Q补偿时,使用常规估算品质因子;当对同一工区的品质因子进行对比时,应换算成同一类品质因子。

关键词: 品质因子; 常规估算; 物理定义; Q-V经验式; Q值修正

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)05-1069-05 doi: 10.11720/wtyht.2015.5.31

Q modification under the situation of strong attenuation

YANG Xiao-Hui¹, LU Hong-Mei², WANG Rong-Juan², MA Yuan-Yuan³, YUAN Dian³, CUI Zhen³, HE Yuan³

1.Geophysical Research Institute,SINOPEC,Nanjing 210014,China

2.Exploration & Production Research Institute,SINOPEC,Beijing 100083,China;

3.School of Geophysics and Information Engineering,China University of Petroleum,Beijing 102249

Abstract

Quality factor ( Q) is a key parameter for geophysical exploration in that it indicates the magnitude of sediment attenuation.When attenuation is large,quality factor computed by conventional methods such as spectral ratio method is smaller than 2π,which is the low limit of Q calculated by defining expression.Conversion formula for the two quality factors is introduced by investigating the differences between them.Model tests indicate that,when quality factor is lower than 30,relative error between quality factors calculated by two methods is larger than 10% so that they should be distinguished one from another.Based on this study,the authors put forward some advises.First,during Q-V fitting process,it is prefer to use the quality factors calculated by defining expression.Second,conventional method is preferred in gaining quality factors in reverse Q compensation process.Third,when the comparison of quality factors is needed in an oil field,quality factors should be converted to the same class before the comparison.

Keyword: quality factor; conventional estimate method; physical defining expression; Q-V empirical formula; Q modification

Show Figures

品质因子Q是衡量地层介质对地震波吸收衰减强弱的属性参量, 在反Q滤波提高分辨率、流体检测和储层预测等方面有着重要的应用^[1]。在近地表(尤其是沙漠工区), 由于砂层疏松未固结等原因, Q值往往较小; 当近地表较厚时(如准噶尔盆地和川西坳陷的低速带和降速带, 总厚度可达上百米), 表层介质对地震波的吸收衰减是很可观的, 甚至可能导致单炮记录的主频只有十几Hz, 大大影响了中深层的成像精度^[2]。反Q滤波是补偿吸收衰减、提高地震成像精度的有效手段, 从Hale最早提出相位校正、振幅补偿的全反Q滤波方法^[3]以后, 大量学者提出了不同的补偿算法, 如对衰减函数作级数展开的全反Q滤波技术^[4]、基于波场延拓的全反Q滤波技术^{[5, 6, 7]}等, 目前应用较多的是稳定反Q滤波技术^[8], 如Wang^[9]引入稳定性因子, 较好地解决了补偿过程中振幅溢出、噪声放大等不稳定问题。表层反Q滤波的前提是需要相对准确的地表Q值分布, 因此Q值是近地表结构调查的一个主要对象。

根据品质因子Q值的物理定义, Q值反比于地震波传播一个波长后的能量损失率, 其值在理论上不小于2π 。在实际工作中, 人们一般采用地震波谱方法来估算地层Q值, 如对数谱比法(LSR)^{[10, 11, 12]}、质心频移法(CFS)^[13]和属性组合法^[14]等, 取得了较好的应用实效。根据已发表文献, 利用上述方法估算的低速带Q值一般分布在1~10之间^[15], 很多情况下低于理论极小值。理论定义与实际估算之间的这种差异, 主要是因为当Q值较小(即强衰减条件)时, 近似估算的假设条件不再成立。王国庆等^[16]定量分析了这种误差, 对实际估算的小Q值进行了校正, 并重新给出了黄土塬、沙漠及平原近地表的真实Q值分布, 使其数值符合物理定义。笔者认为, 这种定量校正统一了实际估算与物理定义得到的Q值, 使人们对于Q值分布有更清晰的认识, 具有较好的理论意义和实用价值。

这里, 在文献[16]的基础上, 对Q值修正进行更深入的定量分析, 通过换算公式实现理论定义和实际估算之间Q值的转换, 并指出了当实际估算Q值小于30时, 这种换算是必要的, 理清两者的概念和适用范围, 对于实际应用具有一定的指导意义。

1 基本原理

记初始子波谱为A₁(f), 经地层传播距离s后, 衰减为A₂(f), 两者关系满足

$\begin{matrix} A_{2} (f) = A_{1} (f) e^{- α (f) s}, (1) \end{matrix}$

式中α (f)是与频率f有关的地层吸收系数。在地震频段范围内, 该变量与频率呈近似正比关系, 因此式(1)可改写为

$\begin{matrix} A_{2} (f) = A_{1} (f) e^{- γfvt} = A_{1} (f) e^{- (πft \frac{)}{(} Q_{R})}, (2) \end{matrix}$

其中:γ 是与对数衰减量有关的常量, v是地层速度, t为传播s的时间, Q_R= $\begin{matrix} \frac{π}{γv} \end{matrix}$ = $\begin{matrix} \frac{πf}{α (f) v} \end{matrix}$ 。需要说明的是, 式(2)是对式(1)的变形改写, 不存在数学上的近似处理, 一般地, Q值估算和反Q滤波中的振幅补偿算法都是基于式(2)进行推导。根据实际地震资料, 利用常规Q值估算方法(如谱比法、质心频移法等)估算得到的品质因子即为Q_R。

根据地层品质因子的物理定义, 有

$\begin{matrix} Q_{p} = 2 πE / ΔE, (3) \end{matrix}$

式中:Q_p为物理定义品质因子, E为初始子波的能量, Δ E为子波传播1个波长后衰减的能量。联合式(2)和式(3), 可得

$\begin{matrix} e^{- 2 π / Q_{R}} = 1 - 2 π / Q_{p} 。 (4) \end{matrix}$

式(4)将Q_R和Q_p联系起来, 使得两者的异同更加明显。当式(4)中的指数项按Tayler一阶级数展开时, 则Q_p≈ Q_R, 即物理定义的品质因子与常规估算的品质因子近似相等。Tayler展开的数学近似条件是e^-^x(x> 0)的指数x为一小量, x值越大, 误差越大; 相应地, 式(4)中的2π /Q_R越大(即Q_R越小), 一阶展开误差越大, Q_R和Q_p的差异越大, 下面主要通过定量分析来讨论两者的异同。

2 模型测试

下面, 通过模型测试来说明物理定义的品质因子Q_p和常规估算的品质因子Q_R之间的异同。不失一般性, 以50 Hz主频的Ricker子波作为初始地震子波, 假设其在一足够厚的常Q介质中传播一个周期(约为20 ms), 衰减方式见式(2), 通过总能量的衰减率来考察Q_p和Q_R的差异。

第一种情况:取Q_R=100, 图1展示了衰减前后的波形及频谱。从波形上看, 子波主能量略有降低, 峰值从3 503减为3 382; 从频谱上看, 主频由50.0 Hz下降为49.5 Hz。数值计算得到衰减后总能量的衰减率(Δ E/E)约为0.064 4, 按式(3)换算得Q_p为97.50, 与Q_R的相对误差为2.50%。此时, 常规估算的Q_R(例如用谱比法估算)和物理定义的Q_p之间可以互通, 不作区分。

	Figure Option View Download New Window
	图1 Q=100衰减前后的波形(a)及频谱(b)

第二种情况:取Q_R=10, 图2展示了衰减前后的波形及频谱。子波峰值从3 503衰减为2 485, 主频由50.0 Hz衰减为46.5 Hz, 这相当于初始子波能分辨5 ms(四分之一波长)的薄层, 衰减子波只能分辨5.37 ms的薄层, 波形分辨率降低了近7.5%。数值计算的衰减后总能量的衰减率(Δ E/E)约为0.475 7, 按式(3)换算得Q_p为13.21, 与Q_R的相对误差为32.10%。此时, 常规估算的Q_R和物理定义的Q_p之间互通性较差, 应区别对待。

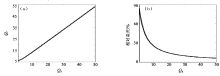
	Figure Option View Download New Window
	图2 Q=10衰减前后的波形(a)及频谱(b)

实际上, 根据式(4)可以实现Q_R和Q_p之间的数值换算, 例如, 当利用常规方法估算得到一组Q_R值, 可以通过该式换算得到符合物理定义的Q_p值, 便于与实验室物理模型数据进行对比; 反之, 亦然。图3a展示了Q_R和Q_p之间的关系曲线, 其中, 横轴为Q_R值(从1渐变到50), 纵轴为Q_p; 图3b为两者的相对误差曲线, 即 $\begin{matrix} \frac{| Q_{R} - Q_{p} |}{Q_{p}} \end{matrix}$ × 100%。图3a表明, 随着Q_R的增加, Q_p也相应增加, 但两者数值存在一定的差异。例如, 当Q_R=8时, Q_p=11.55; 当Q_R=40, Q_p=43.22。图3b表明, 随着Q_R的增加, 其与Q_p的相对误差逐渐减小, 数值从初始的84.11%降为6.04%, 下降速度逐渐趋于平缓。当Q_R< 30时, 其与Q_p的相对误差大于10%, 笔者认为两者不可混用, 应区别对待。

	Figure Option View Download New Window
	图3 Q_R和Q_p关系(a)及其相对误差(b)

3 Q值修正

在实际生产中, 人们主要按照式(2)来估算品质因子(如对数谱比法等), 这时得到的应该是Q_R。在近地表调查中, Q_R一般小于20, 不能近似地看作是具有物理意义的品质因子Q_p。因此, 需要利用式(4)对强衰减条件下的小Q值进行修正, 这样做是为了便于与实验室物理模型数据进行比对或用作其他用途。下面摘录几组地区的地层小Q值进行修正, 作为示例。

表1 濮城地层结构调查

表1是濮城地层结构调查结果^[17], 第2~4列给出了前4层的厚度、速度和Q值等信息(这里的Q值即本文的Q_R); 第5列是根据式(4)转换得到的地层Q_p。可以看到, 实际估算的浅地表品质因数为1.48和4.55, 经等价换算后得到具有物理意义的地层真实品质因数, 分别为6.37和8.39, 换算前后的差异较为明显; 下面2层的品质因数换算前后相差不大, 可以不作区分。表2是大庆工区表层调查结构^[18], 陆地的品质因数略大于沼泽, 从换算结果看, 3层低速带品质因子(小于30)的换算是非常有必要的, 尤其是当Q_R< 2π 时。

表2 大庆近地表调查

4 Q-V经验公式

为了适应三维工区的生产需求, 人们往往借助Q-V经验公式来得到地层的三维Q体, 而Q-V经验式需要通过离散点的拟合来获得。从实际资料中得到的往往是Q_R, 而我们需要拟合的应该是具有物理意义的Q_p-V经验式, 因此, 在拟合之前进行Q_R-Q_p的换算是非常有必要的。

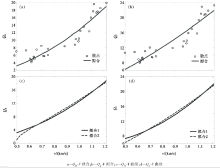
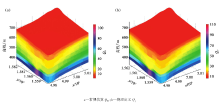
	Figure Option View Download New Window
	图4 Q-V经验式拟合

结合实例来说明。图4a中散点是某工区近地表Q_R-V分布(品质因子由谱比法估算得到), 值域区间为[4, 20], 实线是对该分布直接进行拟合, 拟合得经验式为Q_R=12.70V^2.0。图4b中散点是根据图4a中Q_R-V转换得到的Q_p-V分布, 值域区间为[7.8, 23.8], 实线为拟合曲线, 经验式为Q_R=16.50V^1.4。图4c和图4d展示了两个经验式的差异, 其中, 实线对应图4a的拟合式, 虚线对应图4b的拟合式。图4c图是将品质因子转换为Q_R进行对比, 图4d图是将品质因子转换为Q_p进行对比, 可以看到, 虚线和实线的趋势基本一致, 但在局部仍存在一定的差异, 尤其是速度小于600 m/s的低速带, 笔者认为第二种拟合方式更具备物理意义。图5是工区近地表及浅层的三维Q体, 其中, 图5a为Q_R, 值域分布区间为[1.25, 106.88], 图5b为Q_p, 值域分布区间为[6.32, 110.06]。

	Figure Option View Download New Window
	图5 近地表及浅层三维Q体

5 结论

常规方法估算的品质因数与物理定义的品质因数存在一定的差异, 当值大于30时, 此时的Q_R可近似替代Q_p; 当值小于30时, 两者的误差将不可忽略, 应加以区分。在实际应用中, 两者需要区别对待, 例如, 进行Q-V经验式拟合时, 建议使用Q_p, 更符合物理定义; 进行表层反Q补偿时, 建议使用Q_R, 因为补偿算法一般根据指数衰减模型实现; 进行不同时期、不同资料得到的品质因子对比时, 建议换算为同一类品质因子(Q_R或Q_p)。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	马昭军, 刘洋. 地震波衰减反演研究综述[J]. 地球物理学进展, 2005, 20(4): 1074-1082. [本文引用:1]
[2]	涂远艮, 王达远, 李华科. 川西坳陷地震波衰减定量估算及分析[J]. 物探与化探, 2013, 37(4): 596-602, 632. [本文引用:1]
[3]	Hale D. An inverse- Q filter[J]. Stanford Exploration Project Report, 1981, 26: 231-243. [本文引用:1]
[4]	Hale D. Q-adaptive deconvolution[J]. Stanford Exploration Project Report, 1982, 30: 133-158. [本文引用:1]
[5]	Hargreaves N D, Calvert A J. Inverse Q filtering by Fourier transform[J]. Geophysics, 1991, 56(4): 519-52. [本文引用:1]
[6]	郭见乐. 基于粘滞性声波方程的吸收补偿方法[J]. 物探与化探, 2014, 38(3): 577-581. [本文引用:1]
[7]	郭恺, 娄婷婷. 双复杂介质条件下的反 Q滤波偏移延拓算子研究[J]. 物探与化探, 2014, 38(3): 571-576. [本文引用:1]
[8]	王珊, 于承业, 王云专, 等. 稳定有效的反 Q滤波方法[J]. 物探与化探, 2009, 33(6): 696-699. [本文引用:1]
[9]	Wang Y H. A stable and efficient approach to inverse Q filtering[J]. Geophysics, 2002, 67: 657-663. [本文引用:1]
[10]	Kjartansson E. Constant Q-wave propagation and attenuation[J]. J Geophys Res, 1979, 84: 4737-4748. [本文引用:1]
[11]	王慧茹. 谱模拟频谱比法反演品质因子稳定性分析[J]. 物探与化探, 2009, 33(1): 85-87. [本文引用:1]
[12]	付勋勋, 张君学, 陈阵, 等. 基于S变换求取地层的品质因子 Q[J]. 物探与化探, 2013, 37(1): 113-116. [本文引用:1]
[13]	Quan Y L, Harris J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. [本文引用:1]
[14]	赵宁, 曹思远, 王宗俊, 等. 频域统计性属性组合提取品质因子 Q[J]. 石油地球物理勘探, 2013, 48(4): 545-552. [本文引用:1]
[15]	罗春喜, 程增庆, 王永哲, 等. 地震激发井深与品质因数的关系[J]. 中国煤田地质, 2007, 19(2): 56-58. [本文引用:1]
[16]	王国庆. 近地表衰减的模型实验研究[D]. 北京: 中国石油大学(北京), 2014: 17-19. [本文引用:1]
[17]	钱绍瑚, 高建华, 谷永兴, 等. 地层吸收衰减模型的制作及补偿方法的研究[J]. 石油地球物理勘探, 1998, 33(s1): 18-24. [本文引用:1]
[18]	付德华. 大庆探区近地表地震信号吸收衰减规律研究[D]. 大庆: 大庆石油学院, 2008: 46-59. [本文引用:1]

2005

0.0

马昭军, 刘洋. 地震波衰减反演研究综述[J]. 地球物理学进展, 2005, 20(4): 1074-1082.

A great progress has been made in research on seismic attenuation over fifty years of development. In this paper, it summarizes attenuation principle of seismic wave, general theories on attenuation and main factors that affect seismic attenuation. The methods of inversion on seismic attenuation are emphasized. At last, the development tendency on research of seismic attenuation is forcasted.

对地震波衰减的研究经过近五十年的发展已经取得了不少进展.本文简述了地震波的衰减机制、有关衰减的基本理论以及影响地震波衰减的主要因素，重点概括了地震波衰减的反演方法，最后预测了地震衰减研究的发展趋势.

... 品质因子Q是衡量地层介质对地震波吸收衰减强弱的属性参量,在反Q滤波提高分辨率、流体检测和储层预测等方面有着重要的应用^[1] ...

2013

0.0

涂远艮, 王达远, 李华科. 川西坳陷地震波衰减定量估算及分析[J]. 物探与化探, 2013, 37(4): 596-602, 632.

In western Sichuan basin depression, the marine facies target layers are buried in great depth, resulting in narrow frequency band of reflected seismic data. Hence seiemic resolution can not meet the need of prospecting goals, and low seismic resolution is responsible for stratigraphic absorption attenuation. In order to understand completely the reason for the attenuation of seismic waves, the authors built a model for western Sichuan basin depression strata, then calculated quantitatively spherical divergence, absorption and transmission attenuation of seismic wave based on the model, and combined the calculated attenuation values with seismic data, VSP and Walkway-VSP data to analyze the factors affecting high frequency reflected signal acquisition recording of deep layers. It turns out that the serious absorption attenuation of shallow strata above 1500 meters is the fundamental cause responsible for high frequency component losses of deep layers in western Sichuan basin depression and, as for the marine facies target layers buried deeper than 5000 meters, field acquisition data can only reach about 40Hz frequency band. Therefore, the field acquisition methods aiming at deep target layers should focus on reducing background noises and increasing acquisition density to enhance weak reflection signals of deep layers so as to improve the seismic prospecting precision, rather than solely focus on improving the seismic resolution.

Southwest Exploration and Production Research Institute, Southwest Branch Company of SINOPEC, Chengdu 610000, China

川西坳陷海相勘探目的层埋藏较深,反射资料频带窄,地震分辨率无法满足勘探要求,地层吸收衰减是导致分辨率低的主要原因,为了解深层地震波的衰减情况,首先根据低降速带资料和测井资料建立川西坳陷地层模型,然后定量估算球面扩散、吸收衰减和透射损失引起的地震波衰减量,以估算的衰减值为参考,同时结合地震采集资料、井中零偏VSP和Walkway-VSP资料来分析影响深层反射波高频信号接收的因素。分析指出1 500 m以上浅层强吸收衰减是造成川西坳陷深层反射波高频成分缺失的主要原因,5 000 m以下海相地层反射波频带只能达到40 Hz左右,深层资料采集应以降低背景干扰为重点,并在提高资料采集密度上下功夫,以达到增强深层弱反射信号、提高地震勘探精度的目的,而不应单纯强调提高分辨率。

... 当近地表较厚时(如准噶尔盆地和川西坳陷的低速带和降速带,总厚度可达上百米),表层介质对地震波的吸收衰减是很可观的,甚至可能导致单炮记录的主频只有十几Hz,大大影响了中深层的成像精度^[2] ...

1981

0.0

... 反Q滤波是补偿吸收衰减、提高地震成像精度的有效手段,从Hale最早提出相位校正、振幅补偿的全反Q滤波方法^[3]以后,大量学者提出了不同的补偿算法,如对衰减函数作级数展开的全反Q滤波技术^[4]、基于波场延拓的全反Q滤波技术^[5,6,7]等,目前应用较多的是稳定反Q滤波技术^[8],如Wang^[9]引入稳定性因子,较好地解决了补偿过程中振幅溢出、噪声放大等不稳定问题 ...

1982

0.0

1991

0.0

2014

0.0

2014

0.0

2009

0.0

王珊, 于承业, 王云专, 等. 稳定有效的反 Q滤波方法[J]. 物探与化探, 2009, 33(6): 696-699.

The inverse Q filtering is one of the most effective method for tackling the earth attenuation. Stability and efficiency are two problems of general concern in inverse Q filtering. In this paper, a stabilized inverse Q filtering was implemented and compared with the conventional gain-limited inverse Q filtering by theoretical model and actual seismic data. The results show that the stabilized inverse Q filtering can recover effectively the attenuation of the seismic data and restrict intelligently the attempt to amplify the ambient noise. At the same time, the effects of noise level and specified gain limit Glim on the stabilized inverse Q filtering are also analyzed in this paper.

1.Daqing Petroleum Institute, Daqing 163318,China;2.Exploration and Development Research Institute of Daqing Oilfield CompanyLimited,Daqing 163712,China

反Q滤波是补偿大地吸收衰减有效方法之一，其稳定性和有效性是反Q滤波的前提条件。笔者研究了一种稳定的反Q滤波方法，并通过理论模型和实际数据与传统的增益限制反Q滤波方法进行了对比。结果表明：稳定反Q滤波更好地恢复了衰减的地震信号，并自动限制了对噪声的过渡放大。同时，还分析了噪声和增益限制因子Glim对稳定反Q滤波的影响。

2002

0.0

1979

0.0

... 在实际工作中,人们一般采用地震波谱方法来估算地层Q值,如对数谱比法(LSR)^[10,11,12]、质心频移法(CFS)^[13]和属性组合法^[14]等,取得了较好的应用实效 ...

2009

0.0

王慧茹. 谱模拟频谱比法反演品质因子稳定性分析[J]. 物探与化探, 2009, 33(1): 85-87.

The essential feature of the seismic wave propagation in viscouselastic media is the attenuation of its energy. Generally speaking, the attenuation can be classified into two categories, one is related to the seismicwave propagation, and the other is related to the characteristics of the strata. One of the most important parameters that scale the degree of attenuation is Qfactor. This paper discusses the stability of spectral analogspectrum ratio method to interference and noise.

Institute of Geophysical Exploration, Branch Company of Shengli Oilfield, Dongying257022, China

地震波在粘弹性介质中传播的一个基本特征是能量的衰减及地震波的瞬时波形变化。从广义上说，衰减可分为两类：一类是与地震波传播特性有关的衰减|另一类是反映介质内在属性的地层本征衰减，地层的本征衰减通常用品质因子来度量。反演品质因子的方法有多种，常用的是谱模拟频谱比法。笔者的主要目的是通过模型试算来分析评价该方法在反演品质因子时对干涉和噪声的稳定性，得出有益的结论，用于指导反演计算。

2013

0.0

付勋勋, 张君学, 陈阵, 等. 基于S变换求取地层的品质因子 Q[J]. 物探与化探, 2013, 37(1): 113-116.

It is important to measure quality factor Q in the processing of seismic wave propagation and the predictiing of hydrocarbon. In practical production, the most commonly used to estimate quality factor Q is spectral ratio method. However, the traditional spectral ratio method is facing windowing problem. In this paper, the authors took the advantage of superior time-frequency characteristics of the S-transform and the direct linkage between the Fourier spectrum and the S-transform to extract the corresponding instantaneous spectra of the upper and lower interfaces of the formation. Then by fitting the relationship between frequency and amplitude ratio, the authors estimated the quality factor. Numerical simulation shows the effectiveness of this method.

1. Oil Production Plant NO.2,ChangQing Oilfeild Company,PetroChina,Qingyang 745000,China; 2. ChangQing Oilfeild Company Ultra-low Permeability Reservoirs Research Center,Xi'an,PetroChina,Xi'an 710021,China; 3. Resources and Environmental Department,Southwest Petroleum University,Chengdu 610500,China

地层的品质因子 Q 对衡量地震波传播过程中的能量衰减以及预测油气具有重要意义。生产中最常用的方法是通过频谱比法求品质因子 Q 值,但是传统的频谱比法面临时窗选取等问题。利用S变换优越的时频分析特性以及与傅里叶谱直接相联系的特性,提取地层上下界面对应的瞬时频谱,然后通过拟合频率与振幅比的关系,得到地层的品质因子 Q 值。通过数值模拟证明了该方法的有效性。

1997

0.0

2013

0.0

赵宁, 曹思远, 王宗俊, 等. 频域统计性属性组合提取品质因子 Q[J]. 石油地球物理勘探, 2013, 48(4): 545-552.

本文提出了统计性属性组合法提取地层品质因子的方法。通过研究频域振幅衰减规律，对指数衰减项取泰勒近似展开式，基于频域统计属性组合提出N阶近似式计算Q值的新方法，并对常规的Q值估算方法进行了对比分析。模型试算结果表明，一阶近似式存在一定误差，二阶近似式精度较高。在误差因素分析的基础上，提出应用多次区间拟合式提高Q值精度。由于统计特性的稳定性，依据属性组合提取Q值方法具有较高的稳定性。进一步研究发现，质心频率法是一阶属性组合式的近似。

2007

0.0

... 根据已发表文献,利用上述方法估算的低速带Q值一般分布在1~10之间^[15],很多情况下低于理论极小值 ...

2014

0.0

... 王国庆等^[16]定量分析了这种误差,对实际估算的小Q值进行了校正,并重新给出了黄土塬、沙漠及平原近地表的真实Q值分布,使其数值符合物理定义 ...

1998

0.0

钱绍瑚, 高建华, 谷永兴, 等. 地层吸收衰减模型的制作及补偿方法的研究[J]. 石油地球物理勘探, 1998, 33(s1): 18-24.

本文讨论了地层对地震信号选频衰减的原理，并且导出了建立地层吸收衰减模型的公式：D＝－27.29Q(-1)ft0；进而建立了本工区的衰减模型，计算了有关的吸收指数，层频率吸收指数G1=∑D／f，传播距离吸收指数G2＝∑D／H，指出了大地的低通滤波效应是时变的和空变的。为了对地层衰减进行补偿，除采用自然频率较高的检波器外，还采用低截止频率较高的前置滤波器，才能达到提升和补偿高频信息的目的。

... 表1是濮城地层结构调查结果^[17],第2~4列给出了前4层的厚度、速度和Q值等信息(这里的Q值即本文的Q_R) ...

2008

0.0

付德华. 大庆探区近地表地震信号吸收衰减规律研究[D]. 大庆: 大庆石油学院, 2008: 46-59.

为应用PHOENICS数值模拟环空管道内其它流体情况提供借鉴,利用PHOENICS建立幂律流体环空流动的数值模型,将同心环空幂律流体轴向速度数值模拟结果与二维PIV实验结果对比.模拟结果表明:在同心环空管道中当内管静止时,紊流核心区即轴向速度最大值区域靠近内管壁;当内管旋转时,紊流核心区即轴向速度最大值区域靠近外管壁;靠近内管壁处的切向速度最大,且随着内管转速的增加切向速度增大.验证了应用PHOENICS及PIV技术研究非牛顿流体环空流的可行性,最大相对平均误差为5.925%,数值模拟与实验结果吻合良好.

... 表2是大庆工区表层调查结构^[18],陆地的品质因数略大于沼泽,从换算结果看,3层低速带品质因子(小于30)的换算是非常有必要的,尤其是当Q_R#cod#x0003C ...