基于改进遗传算法的双感应测井反演

引用本文

别康, 徐观佑, 万文春, 关文政, 刘迪仁. 基于改进遗传算法的双感应测井反演[J]. 物探与化探, 2015,39(5): 1063-1068.
BIE Kang, XU Guan-You, WAN Wen-Chun, GUAN Wen-Zheng, LIU Di-Ren. The dual induction logging inversion based on improved genetic algorithm[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1063-1068.
Doi:10.11720/wtyht.2015.5.30 复制到剪切板

Permissions

《物探与化探》编辑部

基于改进遗传算法的双感应测井反演

别康^1,², 徐观佑², 万文春³, 关文政^1,², 刘迪仁^1,²

1.油气资源与勘探技术教育部重点实验室,湖北武汉 430100

2.长江大学地球物理与石油资源学院,湖北武汉 430100

3.中石油长庆油田分公司第五采油厂,陕西榆林 718600

刘迪仁(1965-),教授,博士。1986 年毕业于江汉石油学院矿场地球物理专业,获学士学位,2005年毕业于浙江大学电子科学与技术专业,获博士学位。2007~2008年赴美国麻省理工学院(MIT)电子学研究实验室(RLE)作访问研究。主要从事电法测井正反演、复杂储层测井评价及光纤传感技术等方面的理论和应用研究工作。E-mail:liudr666@163.com

作者简介: 别康(1991-),男,长江大学地球物理与石油资源学院地球探测与信息技术专业硕士研究生。 E-mail:kang722@sina.com

收稿日期: 2015-02-05

基金: 国家自然科学基金项目(41474116)

摘要

针对双感应测井受到泥浆侵入和围岩等因素影响,采用小生境技术的改进遗传算法对双感应测井进行原状地层电阻率和侵入半径等参数反演。利用多层层状地层模型对算法进行验证,反演结果能较好地反映地层模型参数。实例资料的应用结果表明,改进遗传算法反演出的地层电阻率使测井解释结论更加接近试油结论。

关键词: 感应测井; 小生境技术; 遗传算法; 地层电阻率; 反演

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)05-1063-06 doi: 10.11720/wtyht.2015.5.30

The dual induction logging inversion based on improved genetic algorithm

BIE Kang^1,², XU Guan-You², WAN Wen-Chun³, GUAN Wen-Zheng^1,², LIU Di-Ren^1,²

1. Key Laboratory of Exploration Technologies for Oil and Gas Resources of Ministry of Education, Wuhan 430100, China

2. College of Geophysics and Oil Resource, Yangtze University, Wuhan 430100, China

3. No. 5 Oil Production Plant, Changqing Oilfield Company, PetroChina, Yulin 718600, China

Abstract

For the reason that dual induction logging method will be affected by such factors as mud invasion and wall rocks, an improved genetic algorithm based on niche technology is proposed to perform inversion of virgin formation resistivity, invasion radius and other formation parameters. The multiple layered medium is set as model to conduct algorithm verification, The results can well reflect the formation parameters. With the actual dual induction logging data, the new interpretation drawn by the inversion of virgin formation resistivity is more close to the test data.

Keyword: induction logging; niche technology; genetic algorithm; formation resistivity; inversion

Show Figures

地层真电阻率是测井解释评价油气藏的一个重要参数^[1]。双感应测井作为一种被大量应用的常规地层电阻率测井仪器, 在测量过程中由于受到井径、泥浆侵入和上下围岩等因素的影响, 测井响应值往往和地层真电阻率存在一定的偏差。因此, 有必要对双感应测井响应进行反演^{[2, 3, 4]}。

感应测井地层真电阻率反演是一种高度非线性、多极值的全局最优化问题^[3]。当前针对这种问题的主要算法有两种:一种是将目标函数线性化的迭代方法, 算法包括共轭梯度法、SVD法、Marquardt法等, 但这种线性化会导致较大的误差, 加上这些方法对初始值有很高的依赖性, 使得反演的精度有所降低; 另一种是将目标函数不作线性化处理的随机搜索迭代方法, 主要包括蒙特卡洛法、模拟退火法、遗传算法、差分进化算法等智能算法^[5]。近年来, 人们利用智能算法在测井反演方面中已取得了一些成果^{[3, 6]}。遗传算法作为一种较好的非线性智能优化算法, 具备全局寻优和不依赖初始值等特点, 在地球物理反演中应用较为普遍且取得了较好的应用效果^{[6, 7]}, 但标准遗传算法对一些非线性、多峰值问题还是存在不能快速有效地寻找到全局最优的不足。为此, 针对双感应电阻率反演的非线性和多峰值的全局寻优的复杂问题, 采用基于小生境技术的改进遗传算法实现原状地层电阻率和侵入半径等参数反演, 并利用多层层状地层模型验证算法的可行性和可靠性。实际资料进行处理分析的结果表明该算法应用效果明显。

1 反演算法

1.1 双感应测井数理模型及其反演理论

双感应测井反演就是将仪器测到的多条视电阻率曲线通过反演算法得到原状地层真电阻率和侵入半径等地层参数。实现双感应测井反演可以归结为最优化问题的求解, 其极小化目标函数可表示为:

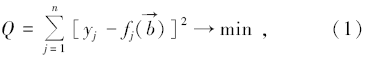
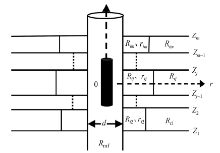
式中:y_j表示测井实测数据, n表示实测电阻率曲线条数, $\begin{matrix} \vec{b} \end{matrix}$ 表示反演的模型参数, f表示正演算子。

如图1所示, 反演模型采用的是在垂直井眼环境下, 考虑泥浆侵入情况的具有轴对称的m层层状地层模型。图中, d为井眼直径, R_mf为泥浆滤液电阻率, R_tj、R_ij和r_ij分别表示第j层的原状地层电阻率、侵入带电阻率和侵入半径, 则式(1)中的 $\begin{matrix} \vec{b} \end{matrix}$ 可以表示为: $\begin{matrix} \vec{b} \end{matrix}$ =(R_t₁, R_t₂, …, R_tj, …, R_t₍_m+₁₎, r_i₁, r_i₂, …, r_ij, …, r_i₍_m+₁₎) 。

	Figure Option View Download New Window
	图1 层状地层模型

针对图1中的轴对称地层模型, 采用Doll几何因子计算双感应正演响应^{[8, 9]}。此次研究的仪器为Atlas的1503双感应测井仪器^{[10, 11]}, 仪器参数见图2。该仪器包括深、中感应线圈系, 深感应采用六线圈系, 即T₃R₁R₂T₂T₁R₃, 中感应采用八线圈系, 即T₃r₅r₄T₂T₁r₃r₁r₂; 线圈匝数的符号表示绕向。

	Figure Option View Download New Window
	图2 双感应测井仪器示意

双感应视电阻率R_a为

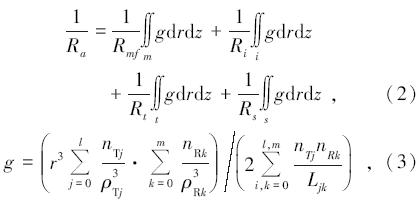
式中:R_s为围岩电阻率, l、m分别表示发射线圈和接收线圈的个数, n_T、n_R分别表示发射线圈和接收线圈的匝数, L表示线圈系之间的距离, ρ _T、ρ _R表示观测点分别到发射线圈和接收线圈的距离。

1.2 改进遗传算法及其实现

遗传算法作为一种典型的智能算法, 在寻优过程中对目标函数没有可微性和连续性等要求, 还因为有较好的鲁棒性、并行处理能力和全局搜索能力等优点而倍受青睐^[7]。但标准遗传算法一般根据适应度值决定个体的选择, 这使得来自于同一种群的高适应度个体被大量繁殖, 造成算法“ 早熟” 和局部收敛, 而不能得到全局最优解, 特别对于式(1)的这类非线性、多峰值函数更容易出现这种现象。因此, 采用基于小生境技术的改进遗传算法进行反演, 以便得到较为准确的原状地层电阻率等参数, 为后续的测井解释评价提供较准确的地层参数。

小生境技术 $\begin{matrix} ^{[1214]} \end{matrix}$ 的基本思想是:首先给出小生境之间的距离参数L, 然后两两比较种群中每一个个体之间的海明距离, 若小于L, 再比较两者之间的适应度值, 对适应度低的个体实施较强的罚函数(即直接对该个体的适应度赋予一个较小值), 这样在指定的距离L之内的两个个体, 被实施惩罚的个体其适应度变得更差, 在进化后期被淘汰的可能性就更大。这就可以保证在距离L之内将只存在一个优良个体, 达到维持种群的多样性, 也使得个体能够在整个约束空间中分散, 从而避免陷入局部收敛, 得到全局最优。

在寻优过程中, 应在不同进化时期选取不同的交叉概率和变异概率以保证种群的优化程度^{[15, 16]}。在进化初期, 为使种群快速寻优需要较大的交叉概率和变异概率; 在进化后期, 则需要选择较小的交叉概率和变异概率避免最佳个体被误操作。笔者采用自适应交叉变异算子, 使得交叉概率和变异概率随着进化进行而变化。自适应交叉算子见式(4), 自适应变异算子见式(5):

$\begin{matrix} \begin{matrix} P_{c} = \{\begin{matrix} \frac{P_{cmin} + P_{cmax}}{2} + \frac{P_{cmax} - P_{cmin}}{2} \cdot \cos (π \frac{F'_{fit} - F_{fitav}}{F_{fitmax} - F_{fitav}}) & F'_{fit} \geq F_{fitav} \\ P_{cmax} & F'_{fit} < F_{fitav} \end{matrix}, (4) \\ P_{m} = \{\begin{matrix} \frac{P_{mmin} + P_{mmax}}{2} + \frac{P_{mmax} - P_{mmin}}{2} \cdot \cos (π \frac{F_{fit} - F_{fitav}}{F_{fitmax} - F_{fitav}}) & F_{fit} \geq F_{fitav} \\ P_{mm ax} & F_{fit} < F_{fitav} \end{matrix} 。 (5) \end{matrix} \end{matrix}$

其中:P_c_max、P_c_min分别是预先设定的最大、最小交叉概率, P_m_max、P_m_min分别是预先设定的最大、最小变异概率, F_fitmax、F_fitav分别为当前种群最大适应度值和平均适应度值, F'_fit为参与交叉的两个个体中较大的适应度值, F_fit为参与变异个体的适应度值。

改进遗传算法实现步骤如下:

Step1(编码):选择适当的二进制长度按下式对原状地层电阻率和侵入半径进行编码:

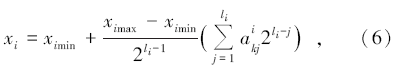
其中:i=1, 2, …, D; D为维度; x_i∈ [x_i_min, x_i_max]; l_i为x_i的编码长度;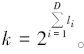

Step2(形成初始种群):随机产生种群个数为M的初始种群。

Step3(计算适应度值):根据下式计算初始种群中所有个体的适应度值, 并令t=0:

$\begin{matrix} F_{fit} (i) = \frac{Q_{\max} - Q (i)}{M \cdot (Q_{\max} - Q_{\min})} (7) \end{matrix}$

其中:Q的计算公式为式(1), Q_max、Q_min分别为当前种群中最大值和最小值。

Step4(选择算法):根据适应度值对M个个体进行降序排列, 记忆前N个个体。

Step5(自适应交叉、变异算法):对初始种群的M个个体进行自适应交叉算子和自适应变异算子, 得到新的M个个体。

Step6(小生境淘汰运算):将Step5中形成的M个个体和Step2中产生的N个个体放在一起, 得到一个含有M+N个个体的新群体。对这个新群体, 按照下式求出每两个个体X_i和X_j之间的海明距离:

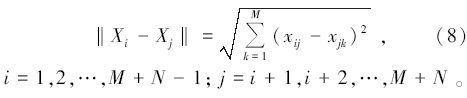
当‖ X_i-X_j‖ < L时, 比较个体X_i和X_j的适应度大小, 并对适应度低的个体施以罚函数:F_min(x_i, x_j)=Penalty; 再依据这M+N个个体的新适应度值重新进行降序排序, 并记忆前N个个体。

Step7(终止条件判断):若理论计算值和实测值的相对误差小于误差阈值ε , 则终止程序, 输出反演结果; 否则, 令t=t+1, 并返回Step4继续运算。

2 模型验证

采用多层层状地层模型对算法进行验证。模型井径d=0.2 m, 泥浆电阻率R_mf=1 Ω · m, 其余参数见表1, R_t, R_i, r_i分别是原状地层电阻率、侵入带电阻率和侵入半径。

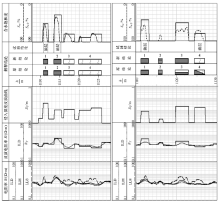
验证采用改进遗传算法, 设定种群个体数M=50, 记忆个体数N=10, 误差阈值ε =0.1%。为验证算法的可行性和稳定性, 将上述模型参数代入反演算法进行计算, 图3给出了双感应测井正演响应曲线和反演结果, 图中ILD、ILM分别为深感应和中感应测井响应, R_T、D_I分别表示反演得到的原状地层电阻率和侵入半径。

	Figure Option View Download New Window
	图3 双感应测井正演响应和反演结果

从图3a中可以看出, 由于侵入带的存在, 深感应电阻率均不能反映出原状地层电阻率, 而且当目的层和围岩的电阻率相差越大, 双感应响应值和原状地层电阻率值相差就越大。为得到准确地层参数, 有必要对测量值进行反演。从图3b和图3c中可以看出, 通过基于小生境技术的改进遗传算法反演出来的原状地层电阻率和侵入半径基本上都在真值附近, 能够较好地反映地层真实情况。

3 应用实例

将改进遗传算法应用到某油田。图4为该油田D24、D28井的反演结果, 图中ILD、ILM和LL8分别表示实际测量的深感应、中感应和八侧向测井资料; R_T和D_I分别表示反演得到的原状地层电阻率和侵入深度; S_w是根据ILD计算得到的含水饱和度, S_w1是根据R_T计算得到的含水饱和度。

	Figure Option View Download New Window
	图4 D24井(a)、D28井(b)实际双感应测井资料反演结果及解释成果

图4a是D24井的1 108~1 228 m深度段双感应测井资料反演结果。1号层和2号层的深感应电阻率和中感应电阻率相差不大, 侵入不明显, 不利于用径向电阻率幅度差进行油水层判断。经过双感应电阻率反演处理后的1号层的地层真电阻率为 2.815 Ω · m(反演前的深感应电阻率峰值为2.658 Ω · m), 含油饱和度为47.560%(反演前计算为 45.248%), 2号层的地层真电阻率为6.893 Ω · m(反演前的深感应电阻率峰值为6.382 Ω · m), 含油饱和度为69.988%(反演前计算为64.949%), 相比原始深感应电阻率峰值, 反演得到的地层电阻率都有所增大, 且反演后的含油饱和度都高于反演前的结果。1号层和2号层合试日产油11.80 t, 试油结论为油层, 表明经反演处理后的解释结论更加符合试油结论。

表1 多层地层模型参数

层号	$\begin{matrix} \frac{层厚}{m} \end{matrix}$	$\begin{matrix} \frac{r_{i}}{m} \end{matrix}$	$\begin{matrix} \frac{R_{i}}{Ω \cdot m} \end{matrix}$	$\begin{matrix} \frac{R_{t}}{Ω \cdot m} \end{matrix}$
1		0	20	20
2	5	0.4	60	120
3	3	0	20	20
4	4	0.5	55	100
5	3	0	20	20
6	2	0.2	40	90
7	3	0	20	20
8	3	0.4	30	50
9	3	0	20	20
10	4	0.3	40	30
11		0	20	20

表1 多层地层模型参数

图4b是D28井的1 110~1 130 m深度段双感应测井资料反演结果。该深度段渗透层的深感应电阻率都低于中感应电阻率, 显示明显的高侵, 再加上该段电阻率都很低, 如果不结合其他资料很难进行油水层识别。对该深度段进行双感应电阻率反演, 1号层反演得到的地层真电阻率为5.32 Ω · m(反演前的深感应电阻率峰值为3.202 Ω · m), 含油饱和度55.775%(反演前计算为42.118%), 反演电阻率高于原始深感应电阻率, 相比于之前的高侵现象, 反演以后呈现明显的低侵现象, 且反演后的含油饱和度高于反演前的结果。4号层反演得到的地层真电阻率为1.326 Ω · m(反演前的深感应电阻率峰值为1.646 Ω · m), 含油饱和度20.449%(反演前计算为29.599%), 经过反演后, 该层高侵现象更加明显, 且反演后的含油饱和度低于反演前的饱和度。根据试油资料显示, 1号层日产油3.48 t, 试油结论为油层; 4号层日产水1.8 t, 试油结论为水层, 表明经过双感应反演处理以后, 反演得到的电阻率更加接近实际地层情况。

将基于小生境技术的改进遗传算法应用到该油田的6口井中, 其中15层的反演结果见表2, 表2中的符号和图4中的符号含义一致。相对于原始解释结论, 根据反演电阻率得到的新解释结论更加符合试油结论, 说明改进遗传算法反演结果比较可靠, 将该算法应用到油田中, 能为测井解释提供比较可靠的地层参数。

表2 实例资料反演结果和解释成果

井号	层号	$\begin{matrix} \frac{起止深度}{m} \end{matrix}$	$\begin{matrix} \frac{ILD}{Ω \cdot m} \end{matrix}$	$\begin{matrix} \frac{ILM}{Ω \cdot m} \end{matrix}$	$\begin{matrix} \frac{LL 8}{Ω \cdot m} \end{matrix}$	$\begin{matrix} \frac{R_{T}}{Ω \cdot m} \end{matrix}$	$\begin{matrix} \frac{D_{I}}{m} \end{matrix}$	$\begin{matrix} \frac{S_{w}}{%} \end{matrix}$	$\begin{matrix} \frac{S_{w 1}}{%} \end{matrix}$	原解释结论	新解释结论	试油结论
D14	1	459.9~460.8	3.60	5.19	8.97	3.72	0.31	50.50	52.15	低产油层	低产油层	油层
	2	461.1~462.6	4.88	7.24	12.86	6.57	0.43	35.96	31.01	油层	油层	油层
	3	557~560.5	1.18	2.28	3.61	3.52	0.45	70.58	40.93	水层	油层	油层
	8	578~581.9	1.31	1.97	3.46	1.12	0.37	71.17	76.99	水层	水层	水层
D14-4	3	485.6~487.8	6.47	9.54	16.64	7.38	0.46	31.12	29.13	油层	油层	油层
D14-4	4	491.3~494.4	5.45	8.25	20.69	8.12	0.51	35.23	28.86	油层	油层	油层
D14-9	7	490.3~493	13.65	21.79	24.42	18.16	0.69	22.18	19.23	油层	油层	油层
D29	36	1 174.8~1 179.9	8.74	10.28	19.34	11.55	0.22	43.73	38.04	油层	油层	油层
D29	46	1 222.6~1 227	1.65	1.95	4.85	1.11	0.37	80.62	98.36	油水同层	水层	水层
D33	15	876.6~878.6	26.45	27.72	24.13	28.18	0.40	23.97	23.22	油层	油层	油层
D35	6	979.4~983.5	7.39	9.05	9.37	8.99	0.36	48.59	44.07	油层	油层	工业油层
	8	991.8~993.8	3.82	4.52	6.28	5.19	0.44	62.37	53.51	油层	油层	工业油层
	24	1 197.1~1 199.6	4.70	5.59	4.54	4.21	0.36	70.45	94.12	低产油层	水层	水层
	25	1 204~1 206.8	4.29	4.94	6.70	4.75	0.34	79.42	75.52	低产油层	低产油层	水层
	32	1 255.3~1 257	5.38	6.35	5.70	4.06	0.41	64.85	78.26	油层	低产油层	水层

表2 实例资料反演结果和解释成果

4 结论

(1) 小生境技术的改进遗传算法具有不依赖于初始值的选择、较好的全局最优等优点, 因此采用该算法对双感应测井电阻率的复杂反演问题具有较好的适用性。

(2) 实例资料的应用结果表明该改进遗传算法反演得到的地层电阻率等参数更接近于实际真值, 其应用可为测井解释提供更为准确的地层参数和进一步提高解释符合率。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	成志刚, 孙宝佃, 刘振华, 等. 高分辨率双侧向测井和双感应测井数据联合反演研究与应用[J]. 测井技术, 2010, 34(6): 542-547. [本文引用:1]
[2]	汪宏年, 陶宏根, 王桂萍, 等. 双感应测井资料的快速近似迭代反演[J]. 地球物理学报, 2007, 50(5): 1614-1622. [本文引用:1]
[3]	熊杰, 刘彩云, 邹长春. 基于粒子群优化算法的感应测井反演[J]. 物探与化探, 2013, 37(6): 1141-1145. [本文引用:3]
[4]	汪宏年, 陶宏根, 王桂萍, 等. 双感应测井资料的快速近似迭代反演[J]. 地球物理学报, 2007, 50(5): 1614-1622. [本文引用:1]
[5]	王家映. 地球物理资料非线性反演方法讲座(一)地球物理反演问题概述[J]. 工程地球物理学报, 2007, 4(1): 1-3. [本文引用:1]
[6]	敬荣中, 鲍光淑, 陈绍裘. 地球物理联合反演研究综述[J]. 地球物理学进展, 2003, 18(3): 535-540. [本文引用:2]
[7]	邹长春, 尉中良, 柴细元, 等. 利用遗传算法实现最优化测井解释[J]. 测井技术, 1999, 23(5): 361-365. [本文引用:2]
[8]	张庚骥. 电法测井[M]. 山东: 石油大学出版社, 1996. [本文引用:1]
[9]	仵杰, 庞巨丰, 徐景硕. 感应测井几何因子理论及其应用研究[J]. 测井技术, 2001, 25(6): 417-422. [本文引用:1]
[10]	胡澍. 地球物理测井仪器[M]. 北京: 石油工业出版社, 1991. [本文引用:1]
[11]	冯启宁, 鞠晓东, 柯式镇, 等. 测井仪器原理[M]. 北京: 石油工业出版社, 2010. [本文引用:1]
[12]	杨慧珠, 张世俊, 杜祥. 小生境遗传算法求解多峰问题在反演中应用[J]. 地球物理学进展, 2001, 16(2): 35-41. [本文引用:1]
[13]	班书昊, 杨慧珠. 小生境遗传算法在孔隙介质反演中的应用研究[J]. 石油勘探与开发, 2005, 32(2): 78-81. [本文引用:1]
[14]	Horn J, Nafpliotis N, Goldberg D. A niched pareto genetic algorithm for multiobjective optimization[C]//Evolutionary Computation. IEEE World Congress on Computational Intelligence, Proceedings of the First IEEE Conference on. Orland o Florida: IEEE XPLORE, 1994, 82-8. [本文引用:1]
[15]	Srinvas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[C]//In: IEEE Trans on Systems, Man and Cybernetics, 1994, 24(4): 656-667. [本文引用:1]
[16]	Eiben A E, Hinterding R, Michalewicz Z. Parameter control in evolutionary algorithms[J]. IEEE Trans Evol Comput, 1999, 3: 124-141. [本文引用:1]

2010

0.0

... 地层真电阻率是测井解释评价油气藏的一个重要参数^[1] ...

2007

0.0

... 因此,有必要对双感应测井响应进行反演^[2,3,4] ...

2013

0.0

... 因此,有必要对双感应测井响应进行反演^[2,3,4] ...

... 感应测井地层真电阻率反演是一种高度非线性、多极值的全局最优化问题^[3] ...

... 近年来,人们利用智能算法在测井反演方面中已取得了一些成果^[3,6] ...

2007

0.0

... 因此,有必要对双感应测井响应进行反演^[2,3,4] ...

2007

0.0

... 另一种是将目标函数不作线性化处理的随机搜索迭代方法,主要包括蒙特卡洛法、模拟退火法、遗传算法、差分进化算法等智能算法^[5] ...

2003

0.0

... 近年来,人们利用智能算法在测井反演方面中已取得了一些成果^[3,6] ...

... 遗传算法作为一种较好的非线性智能优化算法,具备全局寻优和不依赖初始值等特点,在地球物理反演中应用较为普遍且取得了较好的应用效果^[6,7],但标准遗传算法对一些非线性、多峰值问题还是存在不能快速有效地寻找到全局最优的不足 ...

1999

0.0

... 遗传算法作为一种典型的智能算法,在寻优过程中对目标函数没有可微性和连续性等要求,还因为有较好的鲁棒性、并行处理能力和全局搜索能力等优点而倍受青睐^[7] ...

1996

0.0

... 针对图1中的轴对称地层模型,采用Doll几何因子计算双感应正演响应^[8,9] ...

2001

0.0

... 针对图1中的轴对称地层模型,采用Doll几何因子计算双感应正演响应^[8,9] ...

1991

0.0

... 此次研究的仪器为Atlas的1503双感应测井仪器^[10,11],仪器参数见图2 ...

2010

0.0

... 此次研究的仪器为Atlas的1503双感应测井仪器^[10,11],仪器参数见图2 ...

2001

0.0

2005

0.0

1994

0.0

1994

0.0

... 在寻优过程中,应在不同进化时期选取不同的交叉概率和变异概率以保证种群的优化程度^[15,16] ...

1999

0.0

... 在寻优过程中,应在不同进化时期选取不同的交叉概率和变异概率以保证种群的优化程度^[15,16] ...