利用指数函数拟合去除扩频激电信号中的电磁耦合感应

引用本文

向毕文, 陈儒军, 淳少恒, 姚红春, 吴宏, 刘卫强. 利用指数函数拟合去除扩频激电信号中的电磁耦合感应[J]. 物探与化探, 2015,39(5): 1053-1058.
XIANG Bi-Wen, CHEN Ru-Jun, CHUN Shao-Heng, YAO Hong-Chun, WU Hong, LIU Wei-Qiang. A new method for removing EM-coupling in spread spectrum induced polarization based on exponential function fitting[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1053-1058.
Doi:10.11720/wtyht.2015.5.28 复制到剪切板

Permissions

《物探与化探》编辑部

利用指数函数拟合去除扩频激电信号中的电磁耦合感应

向毕文¹, 陈儒军¹, 淳少恒¹, 姚红春², 吴宏², 刘卫强¹

1. 中南大学地球科学与信息物理学院,湖南长沙 410083

2. 湖南强军科技有限公司,湖南长沙 410005

陈儒军(1973-),男,贵州思南人,中南大学副教授,主要研究方向为地球物理仪器及信号处理。

作者简介: 向毕文(1989-),男,湖南强军科技有限公司地球物理工程师,研究方向为地球物理勘探。

收稿日期: 2015-01-19

基金: 中央地质勘查基金(12120113095200)

摘要

电磁耦合感应是频谱激电法中一种很强的干扰因素,尤其在低阻区和大极距测量时,影响了探测深度和探测效果。国内目前主要的去除电磁耦合的方法有多频振幅去耦和多频相位去耦,这些方法去耦的原理是基于激电效应和电磁耦合效应在频域内振幅和相位的差异,但去耦效果在电磁耦合感应强烈时并不理想。此次研究从激电效应的模型出发,采取指数函数拟合激电效应的方法,从时域内去除耦合感应,并通过计算去耦后的相位和相对相位与直接进行相对相位校正的结果进行对比,发现进行指数函数拟合后计算得到的相位受电磁感应的影响更小,去耦效果更佳。

关键词: 激电效应; 耦合感应; 指数函数拟合; 相位; 相对相位

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)05-01053-06 doi: 10.11720/wtyht.2015.5.28

A new method for removing EM-coupling in spread spectrum induced polarization based on exponential function fitting

XIANG Bi-Wen¹, CHEN Ru-Jun¹, CHUN Shao-Heng¹, YAO Hong-Chun², WU Hong², LIU Wei-Qiang¹

1. School of Geosciences and Info-physics, Central South University, Changsha 410083, China

2. Champion Geophysical Technology, Changsha 410005, China

Abstract

The EM-coupling is one of the basic interference in the spectral-induced polarization, especially when the working area is covered with lower-resistivity layer or the current electrode spacing is large. It has great impact on the depth of the exploration and the effect of exploration. Recently, most methods to remove the EM-coupling are centered on the multi-frequency amplitude and the multi-frequency phase. These methods are based on the amplitude and the phase difference between the IP effect and the EM-coupling, which do not work well at strong EM-coupling. The authors' work is based on the IP model, and fits the IP effects with exponential function. Then the EM-coupling effects are removed from the time domain data. The phase and the relative phase after removing EM-coupling are confirmed more effectively based on the application in field data.

Keyword: induced polarization effects; EM-coupling; exponential function fitting; phase; relative phase

Show Figures

在地球物理勘探中, 频谱激电法应用日益广泛。然而, 由于耦合感应的存在, 在进行频散率和相位测量的时候, 特别是在低阻区会出现比较强的假激电异常。激电法勘探中, 广义的电磁耦合包括电容耦合和电磁耦合, 电容耦合是由供电导线与大地以及测量导线之间存在的分布电容而引起的假激电异常; 电磁耦合感应是由于供电导线与测量导线以及大地之间存在的自感和互感引起的假激电异常。通常在干燥的野外环境下, 电容耦合的影响远小于电磁耦合, 因此通常说的耦合感应都是指电磁耦合感应。

自1958年J.R.Wait提出变频激电法原理之后, 国外开始研究各种典型情况下(如均匀大地、层状介质)激电工作中的电磁耦合问题 $\begin{matrix} ^{[13]} \end{matrix}$ 。Wait给出了均匀半空间下, 当激电效应和电磁耦合效应相互影响较小时, 从总场中减去电磁耦合效应的方法。

在20世纪七八十年代, Hallof和Coggon等人探讨了基于纯激电效应产生的相位异常在低频附近差异不大或者与频率相关的一次函数, 而耦合感应产生的相位则随频率呈指数函数增加这一特点的去耦方法^{[2, 4]}。与此同时, Pelton等人将激电效应和电磁耦合效应的双Cole-Cole模型进行多项式逼近, 根据激电效应的时间衰减常数大于电磁耦合效应的时间衰减常数来去耦^[5]。近年来, 关于含有电磁耦合效应的激电频谱的正演模拟取得了一些进展, 虽然整体上电磁耦合效应对低频的激电相位影响稍小, 但是即使是在频率小于1 Hz的频带范围内进行激电测量, 仍然存在较严重的电磁耦合效应。采取合适的装置能够在一定程度上降低高频部分耦合感应的影响^[6], 对高频附近的耦合相位有所改进, 但其对低频部分耦合感应的影响仍有待验证。

20世纪60年代, 频率域激电法在国内兴起, 战克、傅良魁、罗延钟等人作了大量开创性的工作 $\begin{matrix} ^{[79]} \end{matrix}$ 。目前国内比较常用的去除耦合感应的方法有三种:一是针对在频率域激电效应振幅随频率对数近似线性增加而电磁耦合振幅随频率呈指数增加, 采取的两频校正 $\begin{matrix} ^{[1012]} \end{matrix}$ ; 二是根据在低频激电效应的相位随频率变化不大而电磁耦合效应随频率迅速增加的特点, 对相位进行线性校正(计算相对相位 $\begin{matrix} )^{[1315]} \end{matrix}$ ; 三是根据电磁耦合效应和激电效应在时间域的差异进行斩波去耦^[16], 该方法存在着去耦的同时去除了激电信息, 且频谱损失严重的缺点。

本文的去耦原理的思想和斩波去耦相近, 但是在处理电磁耦合部分不是直接去除, 而是在时域内对激电效应进行近似, 这样能够在保存一定激电信息的同时, 较好地去除激电效应。

扩频激电法是通过对大地发送扩频信号, 由接收机接收测量电位信息的一种频谱激电法, 其测量参数为电阻率、相对相位以及频散率。目前, 湖南强军科技有限公司利用自主研发的扩频激电发射— 接收系统, 在藏南罗布莎矿区探测到铬铁矿, 取得了良好的勘探效果^[17]。

1 指数函数拟合基础

利用简化的激发极化Cole-Cole模型时间域表达式, 当频率相关系数为C=1时, 写为^[2]

$\begin{matrix} Z (t) = Z_{0} (1 - m e^{- \frac{t}{τ_{1}}}), (1) \end{matrix}$

式中:Z(t)表示Cole-Cole阻抗的时间域形式, Z₀表示频率为0时的Cole-Cole阻抗, τ ₁为描写激电效应的时间常数, t为时间, m为充电率。

当充电足够长时间时(如阶跃充电), 其电位响应可以转化为^[18]

$\begin{matrix} ΔV (t) = Δ V_{0} + Δ V_{IP} (1 - e^{- \frac{t}{τ_{1}}}), (2) \end{matrix}$

式中:Δ V₀为大地的纯电阻响应, Δ V_IP表示激发极化电位差。

根据式(2)可知, 不含其他干扰的激电数据可以利用公式

$\begin{matrix} V = a_{1} + a_{2} e^{a_{3} t} (3) \end{matrix}$

进行拟合。式中a₁、a₂、a₃为待拟合参数, t表示时间, V表示测量电位值。

2 相位和相对相位测量方法

在频谱激电中, 相位测量和振幅测量具有相似性, 都反应的是地质体的信息。不论是激电效应还是耦合感应, 都会对野外激电效应的测量产生影响。纯激电效应产生的相位异常在低频范围(实际测量频率低于1 Hz)随频率变化不大^[19], 但是电磁耦合感应产生的相位异常则随着频率的变化近似呈线性变化^[15]。这也就是之前相位激电法利用多频去耦以及相对相位去耦的原理。

假定φ _d、φ _g分别为低频、高频扩频激电的相位异常, 含有耦合感应和激电效应, 由激电异常产生的低、高频相位异常为φ _dIP、φ _gIP, 电磁耦合产生的低、高频相位异常为φ _dEM、φ _gEM, 则有

$\begin{matrix} \begin{matrix} φ_{gIP} = φ_{dIP} + Δ_{1} (4) \\ φ_{gEM} = k φ_{dEM} + Δ_{2} (5) \\ φ_{d} = φ_{dIP} + φ_{dEM} (6) \\ φ_{g} = φ_{gIP} + φ_{gEM} (7) \end{matrix} \end{matrix}$

式中:Δ ₁、 $\begin{matrix} {Δ_{2}}^{[11]} \end{matrix}$ 分别代表纯激电效应造成的激电响应随频率变化的相位差异和耦合感应造成的高、低频非线性相位差, k表示频比。解以上各式可得

$\begin{matrix} φ_{dIP} = \frac{k φ_{d} - φ_{g}}{k - 1} + \frac{Δ_{1} + Δ_{2}}{k - 1} 。 (8) \end{matrix}$

式(8)的前半部分即为陈儒军等人^[14]描述的相对相位的计算部分, 后半部分为实际的激电异常相位与相对相位的差异。

当频比k=2时, 对式(8)作变换有

$\begin{matrix} φ_{dIP} + φ_{dEM} = \frac{k φ_{d} - φ_{g}}{k - 1} + Δ_{1} + Δ_{2} + φ_{dEM} 。 (9) \end{matrix}$

如式(9)所示, 等号左边为实测相位值, 等号右边为实测相对相位与纯激电响应造成的不同频率的相位差以及耦合感应产生的相位值之和, 耦合感应值越小, 相位与相对相位的差异也越小。

3 野外数据计算结果分析

使用湖南强军科技有限公司的85321A-SIP分布式激电仪, 在河南楸树湾测区进行信号采集(图1), 供电极距为5 200 m, 测量极距为20 m, 测线长2 000 m, 共100个测点。计算了1/16 Hz、2/16 Hz、4/16 Hz、8/16 Hz 4个频点的相位值和频散率值, 以及1/16~2/16 Hz、2/16~4/16 Hz、4/16~8/16 Hz、8/16~1 Hz4组频率的相对相位值, 并取测区中某一供电点的测深数据为例进行分析。

	Figure Option View Download New Window
	图1 野外实际工作布置

	Figure Option View Download New Window
	图2 去耦前的相位响应

3.1 去耦前的各参数分析

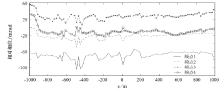
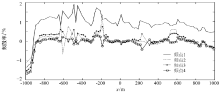
图2所示为直接进行计算得到的同时含有耦合感应和激电效应的相位值, 图中频点1、2、3、4分别对应从低到高的4个频率值(1/16 Hz、2/16 Hz、4/16 Hz、8/16 Hz)。图中显示, 随着频率的增大, 相位值增大, 甚至变成正值, 而根据Cole-Cole模型计算的纯激电响应产生的相位值应为负值^[15], 说明了随着频率的增大, 耦合感应产生的相位异常也越大, 8/16 Hz时的总相位异常整体上比1/16 Hz时的高出80~120 mrad。从第2、3、4个频点的相位值可以看出, 此时的耦合感应产生的相位异常已经明显超过激电相位异常。

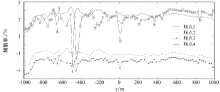
	Figure Option View Download New Window
	图3 去耦前的相对相位

图3显示的是去耦前计算的相对相位, 4组频点的相对相位值也随着频率的升高而升高, 并且在第3组频率时相对相位全部为正值; 利用相对相位去除的耦合感应相位的效果弱于第4组频率。根据式(6)、式(7)可知, 纯激电效应产生的相位异常随频率的变化不大, 说明通过相对相位进行线性校正的相位值不准确, φ _dEM和φ _gEM依然影响明显。

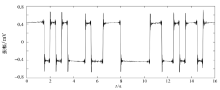
	Figure Option View Download New Window
	图4 去耦前的频散率

图4所示为4组频点计算的频散率曲线, 频点1、4的频散率为正值, 而且频点4的频散率值起伏较大, 可以认为这两个频点的耦合感应影响较小, 频点2、3的频散率均为负值, 且整体趋势与频点1的趋势接近。结合图3和图4, 可以看出频点3处的耦合感应强于频点4。

	Figure Option View Download New Window
	图5 含激电效应和耦合感应的时域波形

采用指数函数拟合, 对含有耦合感应和激电效应的信号波形进行拟合。图6是图5的信号经过指数函数拟合中间激电效应强而耦合感应弱的部分, 得到的耦合感应在时域内的振幅, 进行去耦后能够明显看出激电效应。但是, 由于部分点存在干扰, 去耦以后干扰依然存在, 如图6中的15 s处。

	Figure Option View Download New Window
	图6 指数函数拟合去除耦合感应的时域波形

3.2 去耦后的各参数分析

采取指数函数拟合去耦后, 分别对相位、相对相位和频散率(图7~图9)进行分析。

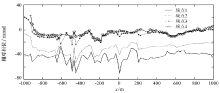
如图7所示, 进行指数函数拟合去耦后相位值随频率变化差异变小, 第1个频率和第4个频率的相位差约50 mrad, 该差异远小于去耦前的120 mrad, 且变化趋势基本一致, 相位值均变成负值。相比去耦前的相对相位约100 mrad的差异, 去耦后的相位值相对于去耦前的相对相位值, 对非线性项的消除也有所改善。

	Figure Option View Download New Window
	图7 指数函数拟合去耦后相位

进行指数函数拟合去耦后, 相对相位的变化情况基本上与相位的变化情况一致。根据式(9)可知, 相位与相对相位的差值主要取决于不同频率的纯激电响应的相位差值以及耦合感应的相位异常值, 这两个值均为正数, 耦合感应越小, 相位与相对相位的差异也越小。对比图7和图8可知, 耦合感应产生的相位异常很小, 从而去耦效果良好。

	Figure Option View Download New Window
	图8 拟合去耦后相对相位

图9所示去耦后频散率整体为正值, 且变化趋势整体一致, 与去耦后相位和相对相位的异常大致呈负相关关系。

	Figure Option View Download New Window
	图9 拟合去耦后的频散率

4 结论与不足

采取频率相关系数为1时的激电效应模型进行指数函数拟合激电效应, 拟合后的相位以及相对相位值均不含有耦合感应, 去耦效果良好, 特别是低频处的去耦效果更好些。

对比去耦前后的相对相位, 可以明显看出频点3(0.5 Hz)处的相对相位校正效果较好, 使得去耦后的相对相位随频率的增加而缓慢增大。

频率相关系数为其他情况下的模型的激电效应有待分析, 纯激电响应的相位随频率变化的具体关系, 以及相对相位与相位的差异的具体计算仍有待深入了解。

致谢:感谢河南省有色金属地质矿产局第三地质大队杨彦峰副队长、张生旭副总工、王永纪工程师和王正威工程师的现场支持, 感谢湖南强军科技工程师曾佩、常富国、王少华等在数据采集方面的支持。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Wait J R. A phenomenological theory of induced electrical polarization[J]. Canadian Journal of Physics, 1958, 36(12): 1634-1644. [本文引用:1]
[2]	Coggon J H. New three point formulas for inductive coupling removal in induced polarization[J]. Geophysics, 1984, 49(3): 307-309. [本文引用:2]
[3]	Dey A, Morrison H F. Electromagnetic coupling in frequency and time domain induced polarization surveys over multilayered earth[J]. Geophysics, 1973, 38(2): 380-405. [本文引用:1]
[4]	Hallof P G. The IP phase measurement and inductive coupling[J]. Geophysics, 1974, 39(5): 650-665. [本文引用:1]
[5]	Pelton W H, Ward S H, Hallof P G, et al. Mineral discrimination and removal of inductive coupling with multi-frequency IP[J]. Geophysics, 1978, 43(3): 588-609. [本文引用:1]
[6]	Schmutz M, Ghorbani A, Vaudelet P, et al. Cable arrangement to reduce electromagnetic coupling effects in spectral-induced polarization studies[J]. Geophysics, 2014, 79(2): A1-A5. [本文引用:1]
[7]	战克, 王继伦. 变频法中电磁耦合的近似校正方法[J]. 地质与勘探, 1981, 17(4): 40-46. [本文引用:1]
[8]	傅良魁, 张虎豹. 频谱激电若干理论研究[J]. 物探与化探, 1983, 19(6): 410-420. [本文引用:1]
[9]	罗延钟. 利用多频测量作“变频法”电磁耦合校正[J]. 地质与勘探, 1980, 16(10): 43-52. [本文引用:1]
[10]	黄寄洲, 张国鸿. 频率域激电法的电磁耦合校正应用研究[J]. 安徽地质, 2014, 24(3): 205-209. [本文引用:1]
[11]	徐勇, 陈林, 管文慧. 变频法电磁耦合效应校正原理与实例[J]. 西部资源, 2012, (4): 190-191. [本文引用:1]
[12]	崔燕丽, 白宜诚, 罗维斌. 多频去耦在双频激电数据去耦中的应用[J]. 物探与化探, 2006, 30(1): 71-74. [本文引用:1]
[13]	陈儒军, 何继善, 白宜诚, 等. 多频激电相对相位谱研究[J]. 中南大学学报: 自然科学版, 2004, 35(1): 106-111. [本文引用:1]
[14]	陈儒军. 伪随机多频电磁法观测系统研究[D]. 长沙: 中南大学, 2003. [本文引用:1]
[15]	郭鹏, 林品荣, 石福生. 相位激电电磁耦合两频校正技术[J], 物探与化探, 2010, 34(4): 491-492. [本文引用:2]
[16]	付国红. 频率域激发极化法斩波去耦关键技术与理论研究[D]. 长沙: 中南大学, 2007. [本文引用:1]
[17]	Xi X, Yang H, He L F, et al. Chromite mapping using induced polarization method based on spread spectrum technology[C]//Smith S D. Symposium on the application of geophysics to engineering and environmental problems, Denver: Environment and engineering geophysical society, 2013: 13-19. [本文引用:1]
[18]	何继善. 双频激电法[M]. 北京: 高等教育出版社, 2005. [本文引用:1]
[19]	刘飞, 陈辉, 蒋才洋, 等. 含电磁耦合效应的偶极-偶极装置频谱激电效应特征研究[J]. 科技信息, 2014(13): 70-71. [本文引用:1]

1958

0.0

1984

0.0

... 在20世纪七八十年代,Hallof和Coggon等人探讨了基于纯激电效应产生的相位异常在低频附近差异不大或者与频率相关的一次函数,而耦合感应产生的相位则随频率呈指数函数增加这一特点的去耦方法^[2,4] ...

... 1 指数函数拟合基础利用简化的激发极化Cole-Cole模型时间域表达式,当频率相关系数为C=1时,写为^[2] ...

1973

0.0

1974

0.0

1978

0.0

... 与此同时,Pelton等人将激电效应和电磁耦合效应的双Cole-Cole模型进行多项式逼近,根据激电效应的时间衰减常数大于电磁耦合效应的时间衰减常数来去耦^[5] ...

2014

0.0

... 采取合适的装置能够在一定程度上降低高频部分耦合感应的影响^[6],对高频附近的耦合相位有所改进,但其对低频部分耦合感应的影响仍有待验证 ...

1981

0.0

战克, 王继伦. 变频法中电磁耦合的近似校正方法[J]. 地质与勘探, 1981, 17(4): 40-46.

正在变频激电法的解释推断中,电磁耦合的识别与校正是物探工作者十分注意的一个问题.关于偶极装置和中间梯度装置的电磁耦合校正方法已有文章发表.贺来秀三对偶极装置的电磁耦合问题还做了进一步的探讨.我国的邓祖棪同志提出了“高频系数改正法”,罗延钟同志提出了“利用多频测量作变频法电磁耦合的校正法”,都是很有意义的工作.但由于影响电磁耦合的因素很复杂,上述诸方法都只能是近似的方法.通过理论计算和模型实验,我们总结了激电效应和电磁耦合效应各自表现的规律,导出校正公式,制定出具体的校正方法.我们所提出的方法也不例外,仍然是一种近似的方法.现介绍如下.

1983

0.0

傅良魁, 张虎豹. 频谱激电若干理论研究[J]. 物探与化探, 1983, 19(6): 410-420.

This paper deals with transfer function model of spectral induced polarization effect, and presents a mathematical expression for polarization coefficient of a surface polarized body. On such a hasis, the calculating formula and results of complex resistivity on a spheroid in the underground half space are also given, and some regularities of variation in complex resistivity spectra with the change of certain controlling-factors are obtained.

本文讨论了频谱激电效应的传递函数模型,提出了一个面极化体极化系数的数学表达式,并依此给出地下半空间中球体上复电阻率的计算公式和计算结果,得到了复电阻率谱随某些控制因素变化的一些规律.

1980

0.0

2014

0.0

黄寄洲, 张国鸿. 频率域激电法的电磁耦合校正应用研究[J]. 安徽地质, 2014, 24(3): 205-209.

摘　要：通过频率域激电法在已知矿区实际观测结果，发现在第四系覆盖厚度较大的地区视频散率和激电相位参数存在严重的电磁耦合现象，电磁耦合的干扰湮没了激电效应异常，通过多项式法的视频散率校正和双频相位法的激电相位校正，分离出激电效应异常，且异常范围和形态特征与地下隐伏矿体对应的较好，取得了明显的应用效果。。同时根据实际电磁耦合校正工作体会．指出频率域激电法中电磁耦合校正应注意的一些关键技术问题。

2012

0.0

徐勇, 陈林, 管文慧. 变频法电磁耦合效应校正原理与实例[J]. 西部资源, 2012, (4): 190-191.

频率域交流电法广泛运用找矿勘查中,是一种具有不需大电流,轻便、经济等特点的物探勘查方法.该方法在野外抗电磁耦合干扰能力较差,在干扰条件较强的地方难以得到理想数据,给推断解释造成困难.本文作者论述了交流电法中视频散率的电磁耦合效应校正原理,并用实例证明此方法的有效性,最后作者提出了减少电磁耦合的一些方法,对类似项目具有借鉴作用.

2006

0.0

崔燕丽, 白宜诚, 罗维斌. 多频去耦在双频激电数据去耦中的应用[J]. 物探与化探, 2006, 30(1): 71-74.

In the 0.1~10 Hz frequency range of the frequency-domain IP method,the frequency characteristics of the apparent resistivity amplitude determined only by IP effect can be approximately expressed by a linear function of frequency logarithm,and the variation of apparent resistivity amplitude affected by electromagnetic coupling can also be roughly expressed by a power function of frequency.Therefore,multiple frequency measurement is used to remove electromagnetic coupling effect in the frequency-domain IP method.The SQ-3 dual-frequency IP instrument has four frequency groups,and the frequency used is from 1/13Hz to 8Hz,just in the application area of the two approximate formulas.The authors applied the idea of multiple frequency decoupling to process dual-frequency IP data,and put forward the multiple frequency group decoupling method according to dual-frequency IP characteristics.The application of the method to field data processing shows that the decoupling result is satisfactory.

在频率域激电法所用频段0.1~10Hz范围内,单纯由激电效应决定的视电阻率幅值的频率特性,可近似地表示为频率对数的线性函数;电磁耦合效应使视电阻率幅值发生的变化,可近似表示为频率的幂函数。因此,多频测量法被提出用于频率域激电法的电磁耦合校正。SQ-3型双频激电仪设有4个频组,频率从1/13~8Hz,正处于近似公式适用的范围。将前人多频去耦的思路应用于双频激电数据的处理中,根据双频激电的特点,提出双频仪的多频组电磁耦合校正,经野外实际应用,去耦效果良好。

2004

0.0

陈儒军, 何继善, 白宜诚, 等. 多频激电相对相位谱研究[J]. 中南大学学报: 自然科学版, 2004, 35(1): 106-111.

2n系列伪随机多频信号含有多个在对数坐标上呈等间距分布的主频率,是电法勘探的理想场源.多频激电相对相位谱法采用上述信号作为场源,充分反映了该信号作为电法勘探场源的优点.在多频激电相对相位谱法中,相对相位谱定义为ψr(ω)=[kψ(ω)-ψ(kω)]/(k-1).根据傅里叶变换的性质和激电效应与耦合感应的关系,证明相对相位谱测量具有如下优点:可以消除发送机和接收机之间因时间不同步而引起的测量误差,提高了观测精度;对电磁耦合感应进行了一阶线性校正,可以压制耦合感应.通过改变Cole-Cole模型中的频率相关系数c和频比k来分析相对相位谱与相位谱的差异,发现相对相位谱与相位谱在形态上一致,对异常具有同等的反应能力;它们之间的差值与频比k成反比、与频率相关系数c成正比.野外实测的多频激电相对相位谱和相位谱说明,激电相对相位谱测量对耦合感应具有良好的压制效果.

2003

0.0

陈儒军. 伪随机多频电磁法观测系统研究[D]. 长沙: 中南大学, 2003.

该文在双频激电和伪随机三频激电观测系统研究的基础上,对伪随机多频电磁法观测系统进行了系统研究,研究内容包括伪随机多频信号、多频相对相位谱激电法、计算机仿真技术在电法仪器研制和评价中的应用、伪随机多频电磁法信号的数字信号处理方法、伪随机多频电磁法信号发送机、伪随机多频电磁法信号接收机、伪随机多频电磁法数据采集软件的设计及实现等一系列方法技术.该文在激电相对相位法的基础上提出了激电相对相位谱观测法,并定义了相对相位谱公式.相对相位观测不需要发送机与接收机之间的同步,同时对电磁耦合效应进行了一阶改正.利用伪随机多频...

... 式(8)的前半部分即为陈儒军等人^[14]描述的相对相位的计算部分,后半部分为实际的激电异常相位与相对相位的差异 ...

2010

0.0

郭鹏, 林品荣, 石福生. 相位激电电磁耦合两频校正技术[J], 物探与化探, 2010, 34(4): 491-492.

This paper describes the forward computing method of phaseIP (induced polarization) electromagnetic coupling, which is based on the uniform terrestrial condition. The intermediategradient and dipoledipole device electromagnetic coupling responses are simulated. According to the rule that electromagnetic coupling varies with the working frequency, this paper puts forward an electromagnetic coupling correction means that adopts phases of two frequencies. The effectiveness and the applying effects of the decoupling method are analyzed in combination with practical examples.

介绍均匀大地条件下相位激电电磁耦合的正演方法，模拟计算了中梯和偶极—偶极装置下的电磁耦合响应；根据电磁耦合随频率变化的规律，提出了采用2个频率的相位值进行电磁耦合校正的方法；结合实例，分析了该去耦方法的有效性和应用效果。

... 纯激电效应产生的相位异常在低频范围(实际测量频率低于1 Hz)随频率变化不大^[19],但是电磁耦合感应产生的相位异常则随着频率的变化近似呈线性变化^[15] ...

... 图中显示,随着频率的增大,相位值增大,甚至变成正值,而根据Cole-Cole模型计算的纯激电响应产生的相位值应为负值^[15],说明了随着频率的增大,耦合感应产生的相位异常也越大,8/16 Hz时的总相位异常整体上比1/16 Hz时的高出80~120 mrad ...

2007

0.0

付国红. 频率域激发极化法斩波去耦关键技术与理论研究[D]. 长沙: 中南大学, 2007.

... 三是根据电磁耦合效应和激电效应在时间域的差异进行斩波去耦^[16],该方法存在着去耦的同时去除了激电信息,且频谱损失严重的缺点 ...

2013

0.0

... 接收系统,在藏南罗布莎矿区探测到铬铁矿,取得了良好的勘探效果^[17] ...

2005

0.0

... 当充电足够长时间时(如阶跃充电),其电位响应可以转化为^[18] ...

0.0