电阻率层析成像的二维改进粒子群优化算法反演

引用本文

张倩, 王玲, 江沸菠. 电阻率层析成像的二维改进粒子群优化算法反演[J]. 物探与化探, 2015,39(5): 1047-1052.
ZHANG Qian, WANG Ling, JIANG Fei-Bo. 2-D Improved particle swarm optimization algorithm for electrical resistance tomography inversion[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1047-1052.
Doi:10.11720/wtyht.2015.5.27 复制到剪切板

Permissions

《物探与化探》编辑部

电阻率层析成像的二维改进粒子群优化算法反演

张倩, 王玲, 江沸菠

湖南师范大学物理与信息科学学院,湖南长沙 410081

王玲(1962-),女,湖南长沙人,教授,博士,主要研究方向:频谱激电研究,现代通信技术与网络技术。

作者简介: 张倩(1990-),女,湖南常德人,硕士,主要研究方向:粒子群优化算法、电阻率层析成像反演。

收稿日期: 2014-12-21

摘要

粒子群优化算法(PSO)是通过模拟鸟群觅食过程中的社会行为而提出的一种基于群体智能的全局随机搜索算法,已有研究学者证明PSO算法是一种有效的地球物理反演方法,不依赖初始模型。此次在研究常规粒子群算法的基础上,针对常规粒子群优化算法易于陷于局部极值,后期收敛速度慢,反演精度不高等缺点,提出了一种改进的充分混沌振荡粒子群优化算法。针对粒子群算法的特点,改进速度更新公式,使粒子更快获取与当前全局最好位置的差异,增强粒子的学习能力,并用此算法在matlab2012b编程环境中对均匀半空间电阻率层析成像异常体理论模型进行了二维数值试验。结果表明,此种算法反演时不依赖初始模型,搜索空间增大,实现全局搜索,在准确性上优于标准PSO反演,成像质量优于Levenberg-Marquardt法反演。

关键词: 电阻率层析成像; 二维反演; 粒子群优化; 混沌序列; 非线性

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)05-1047-06 doi: 10.11720/wtyht.2015.5.27

2-D Improved particle swarm optimization algorithm for electrical resistance tomography inversion

ZHANG Qian, WANG Ling, JIANG Fei-Bo

College of Physics and Information Science,Hunan Normal University, Changsha 410081, China

Abstract

Particle swarm optimization (PSO) is a global random search algorithm put forward by simulating the flock foraging in the process of social behavior based on swarm intelligence. Researchers have proved that PSO algorithm is an effective geophysical inversion method, and it does not rely on the initial model. Because the conventional PSO is easy to be stuck in relative extremum, slow convergence speed in the late and the inversion accuracy is not high, this paper presented an improved fully chaotic oscillations particle swarm optimization algorithm based on same conventional PSO theory. It improved the formula of updating speed, made the particles getting the difference between the current global best position quickly, enhanced the learning ability of particles. The paper did a two-dimensional numerical test on ERT data in matlab2012b programming environment,the results show that this algorithm inversion is not dependent on the initial model, increases the search space,and have higher inversion in accuracy than the standard PSO, and the image quality is better than that of Levenberg-Marquardt method.

Keyword: electrical resistance tomography(ERT); 2d inversion; particle swarm optimization; chaotic sequence; nonlinearity

Show Figures

电阻率层析成像(ERT)方法由日本科学家Shima^[1]等首先提出并给出反演解释, 具有场源实现简单、实施方便、分辨率高、经济实惠、穿透深度大等优点, 有广泛的应用前景。目前, ERT资料解释还是以线性反演为主^{[2, 3, 4, 5]}, 而ERT反演是复杂的非线性问题。虽然线性反演理论目前已经相当成熟, 但将非线性问题在初始模型附近基于模型空间或数据空间的线性化或拟线性化, 其选取目标函数都是基于最小构造或最大平滑, 在迭代次数、收敛性上存在着不足, 容易陷入局部极值、偏导数矩阵求解困难以及反演效果依赖初始模型等问题^[6], 所得的地电断面对地质边界不能准确地分辨, 给地质解释带来困难。

在ERT的非线性反演研究方面:卢元林等^[7]将模拟退火算法应用到二维电法资料的反演; MADAN等^[8]、FERN'NDEZ等^[9]使用遗传算法实现了电测深曲线的遗传算法反演; LIU等^[10]使用改进的遗传算法进行了三维的电阻率反演; GAD等^[11]、MAITI等^[12]、AHMAD等^[13]和徐海浪等^[14]使用人工神经网络进行了一维或二维电阻率反演的初步研究, 但二维反演时, 存在网格剖分稀疏、反演参数少、规模有限等缺点, 应用仅限于一维电测深数据; FERN'NDE^[15]将粒子群优化算法(PSO)引入一维电阻率反演, 取得了较好的效果; Kim^{[16, 17]}提出了ERT的反演地电4D延时数据算法; Karaoulis^[18]提出了一种改进的4D-ATC 算法, 提高了四维ERT算法的准确性和鲁棒性。但是, 目前三、四维反演很多只局限于理论研究及小规模的模型试算阶段, 且反演时间过长, 工作效率低, 所以实际应用最多的还是一维和二维反演。

此次对ERT的反演就是在二维中进行的。传统的局部搜索方法如共轭梯度法、最小二乘法的搜索空间很小, 且依赖初始模型, 容易陷于局部极值, 因此基于全局搜索的智能算法的研究越来越受到人们的关注。笔者参考了混沌振荡的思想^{[19, 20]}, 提出一种充分混沌振荡PSO算法(FCO-PSO), 在各影响粒子群速度更新的参数中引入混沌搜索, 并用于电阻率层析成像的二维反演。

1 方法原理

1.1 PSO算法

粒子群优化算法(PSO)是在1995年由Kennedy等^[21]提出的基于群体智能的全局随机搜索算法。采用速度— 位置搜索模型, 每个粒子代表解空间的一个候选解, 解的优劣程度由适应度函数决定, 而适应度函数的选取根据具体的优化目标定义。PSO把一群粒子随机初始化, 其中第i(i=1, 2, …, N)个粒子在d维解空间的位置是x_i=( $\begin{matrix} x_{i}^{1} \end{matrix}$ , $\begin{matrix} x_{i}^{2} \end{matrix}$ , …, $\begin{matrix} x_{i}^{d} \end{matrix}$ )。速度v_i=( $\begin{matrix} v_{i}^{1} \end{matrix}$ , $\begin{matrix} v_{i}^{2} \end{matrix}$ , …, $\begin{matrix} v_{i}^{d} \end{matrix}$ )决定在搜索空间单位迭代中的位移。每次迭代中, 每个粒子都是通过动态跟踪个体极值和全局极值来更新其速度和位置, 其中个体极值是粒子从初始到当前迭代次数搜索找到的最优解p_i=( $\begin{matrix} p_{i}^{1} \end{matrix}$ , $\begin{matrix} p_{i}^{2} \end{matrix}$ , …, $\begin{matrix} p_{i}^{d} \end{matrix}$ ), 全局极值是粒子种群目前的最优解g=(g¹, g², …, g^d)。粒子群中的每个粒子根据式(1)、式(2)来更新其速度和位置:

$\begin{matrix} \begin{matrix} v_{i}^{t + 1} = w_{t} \times v_{i}^{t} + c_{1} \times r_{1} \times (p_{i}^{t} - x_{i}^{t}) + \\ c_{2} \times r_{2} \times (g^{t} - x_{i}^{t}), (1) \\ x_{i}^{t + 1} = x_{i}^{t} + r v_{i}^{t + 1} 。 (2) \end{matrix} \end{matrix}$

其中, ω 表示随迭代次数惯性权重因子; r₁、r₂是均匀分布在(0, 1)区间的随机数; c₁、c₂是学习因子; t为迭代次数; r是约束因子, 一般设为1。

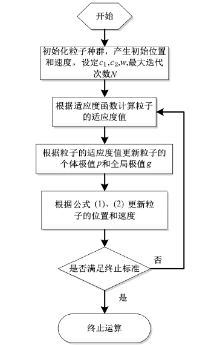
PSO算法是基于群体智能理论的优化算法, 通过群体的粒子间合作与竞争产生的群体智能来指导目标优化搜索(图1)。迭代过程中, 个体极值和全局极值不断更新, 最后得到的全局极值就是算法得到的最优解。

	Figure Option View Download New Window
	图1 粒子群优化算法流程

1.2 改进的充分混沌振荡PSO(FC0-PSO)算法

PSO算法中, r₁、r₂、c₁、c₂和ω 都是影响其收敛好坏的重要因素。标准的PSO收敛速度很快, 但后期表现为趋同性, 易陷于局部极小。因此, 在标准PSO的各个参数中各自引入混沌搜素, 让其充分混沌振荡, 提高PSO算法的收敛速度, 同时避免算法后期振荡。

1.2.1 混沌惯性权重

惯性权重的大小决定粒子对当前速度继承的多少, 选择一个合适的ω 有助于PSO均衡探索能力与开发能力。对较大的ω , 粒子不容易陷于局部极小点, 对较小的ω , 算法容易收敛。 Y.Shi等^[22]提出线性递减惯性权重策略(LDW), Eberhart^[23]提出针对动态优化问题的随机惯性权值, 师学明^[20]证明了一种呈阻尼振荡递减的下降形态ω 有助于PSO跳出局部极值, 加快收敛速度。Logistic方程将混沌引入惯性权重ω 的优化, 实现公式为

$\begin{matrix} \begin{matrix} y (t + 1) = μ \times y (t) \times (1 - y (t)), \\ t = 0, 1, 2, \dots, n (3) \\ ω (t) = ω_{\min} + (ω_{\max} - ω_{\min}) \times [0 . 99^{t} y (t)] 。 (4) \end{matrix} \end{matrix}$

式中:μ 是控制参数, t为迭代次数, ω _max和ω _min是ω 的取值范围, 分别为0.9、0.4。当x(0)∈ (0, 1)、μ =4时, 方程是完全混沌的。已有数值试验证明, 当混沌初值的选择对最终适应度影响不大, PSO算法终能收敛到最优解附近, 文中的混沌初值设为y(0)=0.234。

1.2.2 混沌学习因子与混沌随机数

学习因子c₁和c₂代表了每个粒子本身经验信息和其他粒子经验信息对粒子运行轨迹的影响, 反映了群体间的信息交流。Shi和Eberhart平衡了随机因素的作用, 取c₁=c₂=2。

为了有效提高算法收敛度, 将混沌因子引入到c₁和c₂中:

$\begin{matrix} \begin{matrix} c_{i} (t + 1) = 4 c_{i} (t) \times [1 - c_{i} (t)], (5) \\ c_{i} (t) = c_{\min} + (c_{\max} - c_{\min}) \times [0 . 99^{t} c_{i} (t)] 。 (6) \end{matrix} \end{matrix}$

式中:i=1, 2, c_max=2.05, c_min=1.5。

为克服随机数取值策略带来的低效率, 将混沌引入随机数r₁和r₂:

$\begin{matrix} r_{i} (t + 1) = 4 r_{i} (t) \times (1 - r_{i} (t)) 。 (7) \end{matrix}$

式中:r_i(t)∈ (0, 1), i=1, 2。

1.2.3 混沌粒子初始值和混沌最优解

PSO随机初始化粒子时, 也将混沌序列引入到初始值中用以产生初始粒子的位置和速度, 提高种群的多样性和搜索便利性。另外, 在所有粒子群至今搜到的最优解中引入混沌, 并将此混沌序列中最优解作为粒子更新的位置, 能防止粒子的趋同性, 并使惰性粒子快速跳出局部最优解。

1.3 混沌PSO算法的优化步骤

在标准PSO算法下, 分别在r₁、r₂、c₁、c₂和ω 中引入混沌搜素, 其实现步骤如下。

(1) 初始化算法的参数:粒子群规模N, 最大迭代次数A_Iter, ω 的取值范围[ω _min, ω _max], 学习因子取值范围[c_min, c_max]。根据式(3)~(7)产生r₁、r₂、c₁、c₂和ω 的混沌序列。

(2) 利用混沌序列产生初始粒子的位置和速度。随机产生的在(0, 1)之间的d维向量 $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)代入式(3)logistic映射中, 得到N个不同轨迹的混沌序列作为初始群。然后将 $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)各个分量通过 $\begin{matrix} p_{i}^{d} \end{matrix}$ (t)= $\begin{matrix} p_{\min}^{d} \end{matrix}$ +( $\begin{matrix} p_{\max}^{d} \end{matrix}$ - $\begin{matrix} p_{\min}^{d} \end{matrix}$ )× $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)逆映射到对应变量的取值范围内。计算粒子适应度, 从N个初始化种群选取性能好的M个位置作为初始值, 随机产生M个初始速度。

(3) 比较粒子的当前适应度值F( $\begin{matrix} x_{i}^{d} \end{matrix}$ )和个体极值适应度F( $\begin{matrix} p_{i}^{d} \end{matrix}$ ), 若优于后者, 更新 $\begin{matrix} p_{i}^{d} \end{matrix}$ 。比较更新后的F( $\begin{matrix} p_{i}^{d} \end{matrix}$ )和全局极值适应度F(g^d), 若优于后者, 更新g^d。

(4) 根据式(1)和(2)更新粒子的速度和位置。其中的ω 、r₁、r₂、c₁和c₂依次取步骤1中产生的混沌序列。

(5) 混沌优化全局极值g^d。将g^d映射到(0, 1), 即 $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)=(g^d- $\begin{matrix} x_{\min}^{d} \end{matrix}$ )/( $\begin{matrix} x_{\max}^{d} \end{matrix}$ - $\begin{matrix} x_{\min}^{d} \end{matrix}$ ), 其中[x_min, x_max]为粒子位置的取值范围。将 $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)代入式(3)logistic映射中进行迭代, 产生混沌变量。通过g^d(t)= $\begin{matrix} x_{\min}^{d} \end{matrix}$ +( $\begin{matrix} x_{\max}^{d} \end{matrix}$ - $\begin{matrix} x_{\min}^{d} \end{matrix}$ ) $\begin{matrix} Z_{i}^{d} \end{matrix}$ (t)逆映射将混沌变量载波至原解空间。计算在原解空间的混沌变量经历过每一个可行解g^d的适应度值, 获取性能最好的最优解g_best。

(6) 用g_best替代当前种群任一粒子的位置。

(7) 判断是否满足精度需求或已达到最大迭代次数, 满足输出全局极值, 否则返回步骤3。

2 二维电阻率层析模型反演

针对电阻率层析成像进行了二维FCO-PSO非线性反演, 具体的反演实验方案如下。

2.1 反演过程

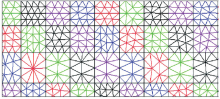
反演方法总是以正演模拟为基础。此次正演过程采用有限单元法(FEM), 其离散化是基于非结构化三角元素, 自动生成三角形网格, 用三角形网格剖分视电阻率数据反演所用的二维地电断面, 如图2。

	Figure Option View Download New Window
	图2 剖分地电断面的三角形网格

假设每个网格中的电阻率和电导率是均匀、齐次的, 而且是各项同性的。一般地下介质的电导率变化范围很大, 电阻率和视电阻率采用对数形式表示, 这样, 数值的变化范围变得很小, 偏导数矩阵稳定性也有所提高, 而且改进使得反演中不会出现视电阻率值和电阻率为负值的情况, 有利于反演的稳定性。反演问题可表示为求最佳模型使目标函数极小:

$\begin{matrix} S = GX - d^{2} + λ^{2} C X^{2}, (8) \end{matrix}$

式中, X代表模型, d代表测点上的观测数据, G代表正演操作, λ 是正则化参数, C是n× n的模型二阶导数矩阵方阵(n是网格单元)。S的第一项(数据失配项)意味着需要在正演得到的所有测点的视电阻率值中找到满足噪声标准的数据模型; 第二项是为了加入先验信息, 引入稳定的反演算法, 创建平滑模型。在求解正则化权衡参数λ 时, 采用了递减方式, 开始时数值较大(默认为0.15), 随着迭代次数增加而减小。

每次迭代计算后, 利用公式

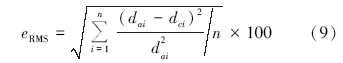
计算数据的均方根误差e_RMS, 其中, d_ai是实测数据, d_ci是模拟数据, i=1, 2, …, n。

2.2 模型反演输出

在上述的反演理论基础上, 建立两个不同的异常体模型来验证反演的结果, 对反演的结果进行分析, 观测数据由正演得到。为了说明观测误差对反演结果的影响, 我们对模型正演的数据分别添加3%的随机噪声。模型基本参数如下:采用Dipole-Dipole装置, 水平方向每排含100个电极, 电极距为 1 m, 竖直方向有14层电阻率数据。

水平方向取值间距:x=(-159.75, -3, 0, 3, 4.5, 6, 7.5, 9, 10.5, 12, 13.5, …, 87, 88.5, 90, 91.5, 93, 94.5, 96, 99, 102, 258.75) 。

竖直方向14层厚度h=(0, 1.5, 3.15, 4.9650, 6.9620, 9.1580, 11.5730, 14.2310, 17.1540, 20.3690, 13.9060, 17.7968, 32.0764, 36.7841)。

为了评价FCO-PSO算法的效率和反演质量的好坏, 对每个电极的数据分别进行Levenberg-Marquardt法(简称L-M法)反演、标准PSO和改进PSO反演。粒子群算法中粒子总数为20, 迭代次数为500, 电阻率取值空间为1~200 Ω · m。

用于验证的模型1为单个地电异常体, 如图3a所示。围岩电阻率为110 Ω · m, 异常体电阻率为 10 Ω · m, 规模为10 m× 5 m, 顶深5 m。用该模型的正演视电阻率作为反演网络的输入, 对网络进行反演测试, 结果见图3b、图3c。

	Figure Option View Download New Window
	图3 单个异常体地电模型及其两种反演方法的成像结果

图中显示, L-M法反演的结果并不是很理想, 虽然能反映出异常中心区域, 但异常边界误差较大且局部区域不收敛; FCO-PSO反演算法能较为准确地反映出异常体的位置、形态, 且反演表现出的电阻率异常模型与实际模型更加接近, 结果优于L-M法的反演。

用于验证的模型2为两个尺寸相同的水平地电异常体, 如图4a所示。围岩电阻率为90 Ω · m, 异常体的电阻率分别为150 Ω · m和50 Ω · m, 规模为6 m× 5 m, 顶深 5 m。用该模型的正演视电阻率作为反演网络的输入, 对网络进行反演测试, 反演结果如图4b、图4c。

	Figure Option View Download New Window
	图4 两个异常体地电模型及其两种反演方法的成像结果

可以看出, L-M法反演虽然能反映出异常中心区域, 但表现出的异常边界误差较大, 且局部区域不收敛, 与理论模型相差过大, 不能准确反映异常体的形态。FCO-PSO反演算法能较为准确地反映出异常体的形态和所处位置, 反演所得电阻率模型与实际模型相对一致, 结果优于L-M法的反演结果。

表1所列为FCO-PSO算法、标准PSO算法和L-M法的性能对比。可以看出: FCO-PSO较标准PSO算法和L-M算法有更低的均方根误差。FCO-PSO算法在各影响寻优参数中引入了混沌振荡, 能够根据结果进行自适应调整, 类似于模拟退火的退火过程, 提高了全局寻优能力, 同时能有效避免早熟收敛, 提高搜索遍历性。

表1 3种反演方法的结果比较

3 结论

(1) 基于混沌振荡的FCO-PSO算法通过各粒子协同合作寻找极值, 基本能准确地反映电阻率层析成像非线性反演的的输入输出特性, 取得较好的反演结果。

(2) 基于全局搜索的FCO-PSO算法避免了对初始模型的依靠和计算偏导数矩阵的问题, 具有较强的适应性, 优于局部搜索技术。

(3) 在标准PSO上, 在各参数中引入混沌搜索做自适应调整, 使得FCO-PSO算法能更精准的逼近全局最优解, 易跳出局部极值, 优于标准PSO算法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Shima H, Sakayama T. Resistivity tomography: An approach to 2D resistivity inverse problem[C]//Expand ed Abstracts of 57th SEG Annual Meeting. New Orleans: Society of Exploration Geophysicists, 1987: 59-61. [本文引用:1]
[2]	Shima H. 2D and 3D resistivity image reconstruction using crosshole data[J]. Geophysics, 1992, 57(10): 1270-1281. [本文引用:1]
[3]	Loke M H, Barker R D. Leastsquares deconvolution of apparent resistivity pseudosections[J]. Geophysics, 1995, 60(6): 1682-1689. [本文引用:1]
[4]	Zohdy A R. A new method for the automatic interpretation of Schlumbeger and Wenner sounding curves[J]. Geophysics, 1989, 54(2): 245-253. [本文引用:1]
[5]	Lesur V, Cuer M, Straub A. 2D and 3D interpretation of electrical tomography measurements. Part 2: The inverse problem[J]. Geophysics, 1999, 64(2): 396-402. [本文引用:1]
[6]	徐海浪, 吴小平. 电阻率二维神经网络反演[J]. 地球物理学报, 2006, 49(2): 584-589. [本文引用:1]
[7]	卢元林, 王兴泰, 王若, 等. 电阻率成像反演中的模拟退火方法[J]. 地球物理学报, 1999, 42(S1): 225-233. [本文引用:1]
[8]	Madan K J, Kumar S, Chowdhury A. Vertical electrical sounding survey and resistivity inversion using genetic algorithm optimization technique[J]. Journal of Hydrology, 2008, 359(1): 71-87. [本文引用:1]
[9]	FERN'NDEZ A J P, FERN'NDEZ M J L, MENÉNDEZ P C O. Feasibility analysis of the use of binary genetic algorithms as importance samplers application to a 1D DC resistivity inverse problem[J]. Mathematical Geosciences, 2008, 40(4): 375-408. [本文引用:1]
[10]	LIU B, LI S C, NIE L C. 3D resistivity inversion using an improved genetic algorithm based on control method of mutation direction[J]. Journal of Applied Geophysics, 2012, 87: 101. [本文引用:1]
[11]	Gad E Q, Keisuke U. Inversion of DC resistivity data usingneural network[J]. Geophysical Prospecting, 2001, 49(4): 417-430. [本文引用:1]
[12]	Maiti S, Erram V C, Gupta G, et al. ANN based inversion of DC resistivity data for groundwater exploration in hard rock terrain of western Maharashtra (India)[J]. Journal of Hydrology, 2012, 464: 294-308. [本文引用:1]
[13]	徐海浪, 吴小平. 电阻率二维神经网络反演[J]. 地球物理学报, 2006, 49(2): 584-589. [本文引用:1]
[14]	FERN'NDEZ M J L, ESPERANZA G G. PSO: A powerful algorithm to solve geophysical inverse problems application to a1DDC resistivity case[J]. Journal of Applied Geophysics, 2012, 71(1): 13-25. [本文引用:1]
[15]	Kim J H. Four dimensional inversion of DC resistivity monitoring data[C]//11th European Meeting of Environmental and Engineering Geophysics. 2005. [本文引用:1]
[16]	Kim J H, Yi M J, Park S G, et al. 4-D inversion of DC resistivity monitoring data acquired over a dynamically changing earth model[J]. Journal of Applied Geophysics, 2009, 68(4): 522-532. [本文引用:1]
[17]	Karaoulis M, Revil A, Tsourlos P, et al. IP4DI: A software for time-lapse 2D/3D DC resistivity and induced polarization tomography[J]. Computers & Geosciences, 2013, 54: 164-170. [本文引用:1]
[18]	Shaw R, Srivastava S. Particle swarm optimization: A new tool to invert geophysical data[J]. Geophysics, 2007, 72(2): F75-F83. [本文引用:1]
[19]	师学明, 肖敏, 范建柯, 等. 大地电磁阻尼粒子群优化反演法研究[J]. 地球物理学报, 2009(4): 1114-1120. [本文引用:1]
[20]	Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. WashingtonDC: IEEE Computer Society, 1995, 4: 1942-1948. [本文引用:2]
[21]	Shi Y, Eberhart R. A modified particle swarm optimizer[C]//Evolutionary Computation Proceedings, 1998. IEEE World Congress on Computational Intelligence. , The 1998 IEEE International Conference on. IEEE, 1998: 69-73. [本文引用:1]
[22]	Eberhart R, Simpson P, Dobbins R. Computational intelligence PC tools[M]. Academic Press Professional, Inc. , 1996. [本文引用:1]

1987

0.0

... 电阻率层析成像(ERT)方法由日本科学家Shima^[1]等首先提出并给出反演解释,具有场源实现简单、实施方便、分辨率高、经济实惠、穿透深度大等优点,有广泛的应用前景 ...

1992

0.0

... 目前,ERT资料解释还是以线性反演为主^[2,3,4,5],而ERT反演是复杂的非线性问题 ...

1995

0.0

... 目前,ERT资料解释还是以线性反演为主^[2,3,4,5],而ERT反演是复杂的非线性问题 ...

1989

0.0

... 目前,ERT资料解释还是以线性反演为主^[2,3,4,5],而ERT反演是复杂的非线性问题 ...

1999

0.0

... 目前,ERT资料解释还是以线性反演为主^[2,3,4,5],而ERT反演是复杂的非线性问题 ...

2006

0.0

... 虽然线性反演理论目前已经相当成熟,但将非线性问题在初始模型附近基于模型空间或数据空间的线性化或拟线性化,其选取目标函数都是基于最小构造或最大平滑,在迭代次数、收敛性上存在着不足,容易陷入局部极值、偏导数矩阵求解困难以及反演效果依赖初始模型等问题^[6],所得的地电断面对地质边界不能准确地分辨,给地质解释带来困难 ...

1999

0.0

... 在ERT的非线性反演研究方面:卢元林等^[7]将模拟退火算法应用到二维电法资料的反演 ...

2008

0.0

... MADAN等^[8]、FERN'NDEZ等^[9]使用遗传算法实现了电测深曲线的遗传算法反演 ...

2008

0.0

... MADAN等^[8]、FERN'NDEZ等^[9]使用遗传算法实现了电测深曲线的遗传算法反演 ...

2012

0.0

... LIU等^[10]使用改进的遗传算法进行了三维的电阻率反演 ...

2001

0.0

... GAD等^[11]、MAITI等^[12]、AHMAD等^[13]和徐海浪等^[14]使用人工神经网络进行了一维或二维电阻率反演的初步研究,但二维反演时,存在网格剖分稀疏、反演参数少、规模有限等缺点,应用仅限于一维电测深数据 ...

2012

0.0

2006

0.0

2012

0.0

2005

0.0

... FERN'NDE^[15]将粒子群优化算法(PSO)引入一维电阻率反演,取得了较好的效果 ...

2009

0.0

... Kim^[16,17]提出了ERT的反演地电4D延时数据算法 ...

2013

0.0

... Kim^[16,17]提出了ERT的反演地电4D延时数据算法 ...

2007

0.0

... Karaoulis^[18]提出了一种改进的4D-ATC 算法,提高了四维ERT算法的准确性和鲁棒性 ...

0.0

... 笔者参考了混沌振荡的思想^[19,20],提出一种充分混沌振荡PSO算法(FCO-PSO),在各影响粒子群速度更新的参数中引入混沌搜索,并用于电阻率层析成像的二维反演 ...

1995

0.0

... Shi等^[22]提出线性递减惯性权重策略(LDW),Eberhart^[23]提出针对动态优化问题的随机惯性权值,师学明^[20]证明了一种呈阻尼振荡递减的下降形态#cod#x003c9 ...

1998

0.0

... 1 PSO算法粒子群优化算法(PSO)是在1995年由Kennedy等^[21]提出的基于群体智能的全局随机搜索算法 ...

1996

0.0