基于高阶双谱的子波整形方法

引用本文

杨振, 文鹏飞, 彭璐, 张宝金. 基于高阶双谱的子波整形方法[J]. 物探与化探, 2015,39(5): 1027-1031.
YANG Zhen, WEN Peng-Fei, PENG Lu, ZHANG Bao-Jin. A method of wavelet shaping based on the high-order bispectrum[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1027-1031.
Doi:10.11720/wtyht.2015.5.24 复制到剪切板

Permissions

《物探与化探》编辑部

基于高阶双谱的子波整形方法

杨振^1,², 文鹏飞^1,², 彭璐³, 张宝金^1,²

1.国土资源部海底矿产资源重点实验室,广东广州 510075

2.广州海洋地质调查局,广东广州 510075

3.中国石化石油物探技术研究院,江苏南京 211103

作者简介: 杨振(1986-),男,硕士研究生,工程师,主要从事海洋地震资料处理工作。E-mail:yangzhen1020@163.com

收稿日期: 2015-02-03

基金: 国家专项项目课题(GZH201200508); 国土资源部海底矿产资源重点实验室开放基金项目(KLMMR-2013-A-17)

摘要

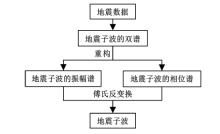
地震子波在地震数据处理中扮演着至关重要的角色,传统的子波提取都是假设子波为最小相位的,但是实际数据中的子波却是混合相位的。为了能够得到一个较为准确、真实的地震子波,笔者采用高阶双谱进行子波重构,然后利用得到的地震子波对叠后数据进行子波整形处理。仿真实验和实际资料试算结果表明,高阶双谱提取的地震子波与实际情况吻合度更高,利用所提取的子波对叠后数据进行处理,可改善剖面的分辨率。

关键词: 高阶双谱; 俞氏子波; 子波整形; 地震资料; 数据重构

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)05-1027-05 doi: 10.11720/wtyht.2015.5.24

A method of wavelet shaping based on the high-order bispectrum

YANG Zhen^1,², WEN Peng-Fei^1,², PENG Lu³, ZHANG Bao-Jin^1,²

1.Key Laboratory of Marine Mineral Resources,Ministry of Land and Resources,Guangzhou 510075,China

2.Guangzhou Marine Geological Survey,Guangzhou 510075,China

3.SINOPEC Geophysical Research Institute,Nanjing 211103,China

Abstract

Seismic wavelet plays a vital role in seismic processing,the traditional wavelet extraction is based on the minimum phase wavelet in seismic data.However,the wavelet in the actual seismic data is of mixed phase.In order to obtain a more accurate wavelet,the authors used high-order bispectrum to reconstruct the seismic wavelet so as to get a more accurate wavelet,and then conducted wavelet shaping processing to improve the vertical resolution of the seismic by using the statistical wavelet.The feasibility of using high-order bispectrum to reconstruct the seismic wavelet was proved by the simulation experiment.Practice shows that the statistical wavelet has good application effect in wavelet shaping processing.

Keyword: high-order bispectrum; Yu wavelet; wavelet shaping; Seismic data; data reconstruction

Show Figures

众所周知, 在地震勘探中, 地震子波反映的是地震波的传播特征, 在地震数据处理中扮演着至关重要的角色。准确的子波估计是地震资料反褶积处理、偏移、特征提取、波阻抗反演、地震资料解释和地震正演模型的基础^[1]。如何能够精确地估计子波是提高地震资料分辨率的重要保证。对于经典的子波提取方法(自相关法、希尔伯特变换法)^{[2, 3]}, 它们都是基于子波为最小相位假设和噪声为高斯白噪声假设。研究表明, 实际地震资料的地震子波大部分是混合相位的^[4], 这违背了经典算法的基本假设, 所以根据经典算法提取的子波也是不准确的。随着勘探精度的提高, 常用的二阶统计方法(自相关、功率谱)提取的子波难以满足实际需求。

提取子波的一个重要用途就是进行子波整形处理^{[5, 6]}, 以此来提高地震资料的分辨率。如何能够统计一个准确的子波就显得至关重要。基于高阶统计量的基本理论, 利用高阶双谱估算子波的振幅谱和相位谱, 最终重构一个准确的子波^{[7, 8]}。这种高阶统计方法, 仅仅根据高阶双谱估算子波, 无需对子波做任何假设, 是一种客观的子波提取方法。运用本文统计的子波进行俞氏子波整形处理, 提高了地震剖面的分辨率。

1 方法原理

前人研究表明, 高阶统计量不但继承了传统二阶统计方法的优点, 还具有三个性质:非高斯、统计独立的随机序列, 它的高阶统计量为常数; 高斯噪声的高阶统计量为零; 随机信号的高阶统计量能够保留它的相位信息。由此可见, 高阶统计量可以提取混合相位子波^[9]。

1.1 子波的双谱

实际地震记录y(n), 由褶积模型可以表示为

$\begin{matrix} y (n) = x (n) + v (n) = w (n) * r (n) + v (n), (1) \end{matrix}$

式中:w(n)为地震子波, r(n)为反射系数, v(n)为噪声。

地震记录y(n)的三阶相关函数, 即三阶统计量^[10]可近似表示为

$\begin{matrix} \begin{matrix} C_{3 y} (τ_{1}, τ_{2}) = C_{3 x} (τ_{1}, τ_{2}) = \\ \frac{1}{N} \overset{N}{\sum_{n = 1}} x (n) x (n + τ_{1}) x (n + τ_{2}), (2) \end{matrix} \end{matrix}$

式中:N为y(n)的采样点数。

对式(2)作二维傅里叶变换, 即可得到地震记录的双谱, 可表示为

$\begin{matrix} B_{x} (ω_{1}, ω_{2}) = \sum_{τ_{1}} \sum_{τ_{2}} C_{3 x} (τ_{1}, τ_{2}) e^{- i (ω_{1} τ_{1} + ω_{2} τ_{2})}, (3) \end{matrix}$

如果v(n)服从高斯分布, 与地震信号x(n)相互独立, 地震记录y(n)的双谱可以表示为

$\begin{matrix} B_{y} (ω_{1}, ω_{2}) = B_{x} (ω_{1}, ω_{2}) = B_{w} (ω_{1}, ω_{2}) B_{r} (ω_{1}, ω_{2}) 。 (4) \end{matrix}$

通常假设反射系数为高斯白噪, 因此地震子波的双谱可表示为

$\begin{matrix} B_{w} (ω_{1}, ω_{2}) = \frac{1}{σ^{2}} B_{y} (ω_{1}, ω_{2}) = \frac{1}{σ^{2}} B_{x} (ω_{1}, ω_{2}), (5) \end{matrix}$

其中:σ 为方差, 且是一个常数, 通常取1^[11]。所以, 知道了地震数据的高阶双谱就可以得到地震子波的双谱。

同时, 可以得到地震子波高阶双谱的振幅谱和相位谱^[12], 分别是

$\begin{matrix} \begin{matrix} | B_{w} (ω_{1}, ω_{2}) | = \sqrt{B_{wr}^{2} (ω_{1}, ω_{2}) + B_{wi}^{2} (ω_{1}, ω_{2})}, (6) \\ ϕ_{w} (ω_{1}, ω_{2}) = \arctan [B_{wi} (ω_{1}, ω_{2}) / B_{wr} (ω_{1}, ω_{2})] 。 (7) \end{matrix} \end{matrix}$

其中:B_w_r(ω ₁, ω ₂)为地震子波双谱的实部, B_w_i(ω ₁, ω ₂)为其虚部。

1.2 子波的振幅重构

通过地震子波的双谱重构地震子波振幅的方法有很多(如递推算法、最小二乘法和DFT法), 其中最小二乘法能够有效避免其他方法中误差传递的缺点, 因此笔者采用经典的最小二乘算法来完成^[13]。

地震子波双谱是对称的, 故可知|B_w(ω ₁, ω ₂)|是两边对称的, 这里只涉及到N/2双谱的计算。令ω ₁=(2kπ )/N, ω ₂=(2lπ )/N, 其中N为采样点个数, 可推导出

$\begin{matrix} \begin{matrix} | B_{w} (ω_{1}, ω_{2}) | = | B_{w} (k, l) | = \\ | W (k) | | W (l) | | W (k + l) |, (8) \end{matrix} \end{matrix}$

其中:k=1, 2, …, N/2; l=k, k+1, …, N/2-k。对式(8)两边取对数, 可以得到

$\begin{matrix} \begin{matrix} \ln | B_{w} (k, l) | = \ln | W (k) | + \\ \ln | W (l) | + \ln | W (k + l) | 。 (9) \end{matrix} \end{matrix}$

式(9)中令ln|B_w (k, l)|=B'_w(k, l), ln|W(k)|=W'(k), 可以得到

$\begin{matrix} B'_{w} (k, l) = W' (k) + W' (l) + W' (k + l) 。 (10) \end{matrix}$

可以看出, B'_w(k, l)和W'(k)呈线性关系, 因此有

$\begin{matrix} B' = A_{m} W' 。 (11) \end{matrix}$

式(11)中:B'是N²/16× 1矩阵, W'是N/2× 1矩阵, A_m为N²/16× N/2阶矩阵。其中, A_m可以表示为

$\begin{matrix} A_{m} = [\begin{matrix} 2 & 1 & 0 & 0 & \dots & 0 & 0 \\ 1 & 1 & 1 & 0 & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ & ⋱ & ︙ & ︙ \\ 1 & 0 & 0 & 0 & \dots & 1 & 1 \\ 0 & 2 & 0 & 1 & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ & ⋱ & ︙ & ︙ \\ 0 & 0 & 0 & 0 & \dots & 0 & 1 \end{matrix}] (12) \end{matrix}$

因为A_m是满秩的矩阵, 故可得

$\begin{matrix} W' = (A_{m}^{T} A_{m})^{- 1} A_{m}^{T} B' 。 (13) \end{matrix}$

其中W'就是求得的子波振幅谱的对数谱^[14], 求其反对数, 由其对称性就可以得到地震子波的振幅谱, 即

$\begin{matrix} | W (k) | = \{\begin{matrix} e^{W (k)}, k = 1, 2, \dots, N / 2 (14) \\ | W (N - k) |, k = \frac{N}{2} + 1, \frac{N}{2} + 2, \dots, N - 1 \end{matrix} \end{matrix}$

其中|W(0)|可通过对每次所选取的样本计算均值获得, 这样就可以得到地震子波的振幅谱|W(k)|。

1.3 子波的相位重构

根据上述振幅重构的推导过程, 可以得到地震子波的相位重构方法, 即

$\begin{matrix} \begin{matrix} ϕ_{w} (ω_{1}, ω_{2}) = ϕ_{w} (k, l) = \\ φ (k) + φ (l) - φ (k + l) 。 (15) \end{matrix} \end{matrix}$

式中:ω ₁=2kπ /N; ω ₂=2lπ /N; k=1, 2, …, N-1; l=k, k+1, …, N-1-k。

由式(15)可以看出ϕ _w(k, l)和φ (k)呈线性关系, 因此就有

$\begin{matrix} ϕ = A_{α} φ 。 (16) \end{matrix}$

式中:ϕ 是N²/4× 1矩阵, A_α是N× 1矩阵, φ 为N²/4× N阶矩阵。其中A_α可以表示为

$\begin{matrix} A_{α} = [\begin{matrix} 2 & - 1 & 0 & 0 & \dots & 0 & 0 \\ 1 & 1 & - 1 & 0 & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ & ⋱ & ︙ & ︙ \\ 1 & 0 & 0 & 0 & \dots & 1 & - 1 \\ 0 & 2 & 0 & - 1 & \dots & 0 & 0 \\ ︙ & ︙ & ︙ & ︙ & ⋱ & ︙ & ︙ \\ 0 & 0 & 0 & 0 & \dots & 0 & 1 \end{matrix}] (17) \end{matrix}$

因为A_α是满秩的矩阵, 故可以得到^[11]

$\begin{matrix} φ = (A_{α}^{T} A_{α})^{- 1} A_{α}^{T} ϕ 。 (18) \end{matrix}$

1.4 地震子波的重构

根据上述过程得到的振幅谱和相位谱, 作傅氏反变换, 即可得到地震子波。具体流程见图1。

	Figure Option View Download New Window
	图1 基于高阶双谱的子波提取流程

2 仿真实验

根据褶积模型, 利用改进的Morlet子波^[15]得到混合相位子波

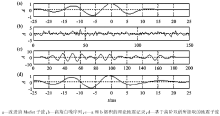
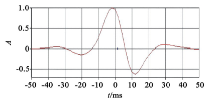
$\begin{matrix} w (t) = e^{imt - 0.5 \times {(ct)}^{2}} 。 (19) \end{matrix}$

其中:m为中心角频率, 为4π ; 当t< 0时, c=2; t> 0时, c=4。反射系数序列采用高斯白噪声序列。基于上述的高阶双谱提取子波算法进行子波提取仿真实验, 结果如图2所示。

	Figure Option View Download New Window
	图2 基于高阶双谱提取的子波

图中原始输入子波(图2a)和用本文方法所提取子波(图2d)的相关系数达到0.9776, 说明基于高阶双谱提取的子波是准确有效的。

3 子波整形处理实际应用

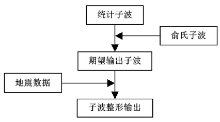
众所周知, 统计出一个较为准确的子波, 除了可以用于反演当中, 还可以用于子波整形。一个准确的子波是子波整形的基础, 是做好子波整形的重要因素。利用统计子波设计一个零相位的整形滤波算子, 把地震数据的子波整形为一个零相位子波, 进而改善地震剖面的分辨率和观感。

	Figure Option View Download New Window
	图3 子波整形流程

利用上述方法统计子波, 并将所统计的混合相位子波整形为俞氏宽频子波^[16], 进而实现子波整形。具体流程如图3所示。

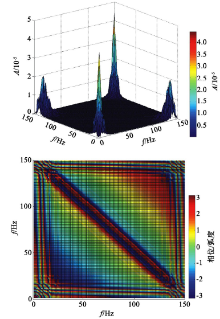
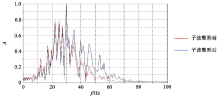
	Figure Option View Download New Window
	图4 高阶双谱的振幅谱(上)及其相位谱(下)

选取南海某探区的叠后成果数据作为原始数据, 从中选取五道地震数据来统计子波。根据上述基于高阶双谱(图4所示)的算法可以得到图5所示的子波。

	Figure Option View Download New Window
	图5 基于高阶双谱统计的地震子波

图6中的左图为输入的目标子波, 即俞氏宽频子波, 可以看出俞氏子波主峰窄, 其旁瓣较小, 而且分辨率较高; 图6中的右图为得到的期望输出子波。将图6中右图所得到的期望输出子波用于原始实际数据, 进行反褶积处理可得到图7所示结果, 从图中可以看出, 经过本文方法的子波整形后, 同相轴更加聚焦, 剖面分辨率得到了明显提高, 在红色和蓝色箭头处, 同相轴得到了很好的分离, 很容易进行准确的层位解释, 为后期工作提供了便利。从整形前后的振幅谱(图8)也可以看出, 经过子波整形处理后的频带宽度得到了拓宽。

	Figure Option View Download New Window
	图6 目标子波(左)和期望输出子波(右)

	Figure Option View Download New Window
	图7 子波整形前(左)、后(右)的剖面对比

	Figure Option View Download New Window
	图8 子波整形前、后的振幅谱对比

4 结论

(1)利用三阶累积量计算高阶双谱, 通过最小二乘法重构子波的振幅谱和相位谱, 进而重构子波, 最终将统计子波应用到子波整形中, 提高了剖面的分辨率。一个准确的估计子波是子波整形的基础, 常规处理系统往往采用自相关法来估计子波, 会造成估计子波的不准确。利用高阶算法能够提高子波估计的准确性, 特别是将高阶算法准确提取子波和俞氏子波整形结合, 进一步加强了子波整形的效果。

(2)通过仿真实验, 输入子波和提取的子波相关系数达到0.977 6, 验证了基于高阶双谱提取子波的准确性。运用估算的子波进行俞氏子波整形处理, 有效地提高了地震剖面的分辨率。

(3)提出的高阶双谱统计子波的方法具有巨大的优势。地震数据的高阶双谱不会将地震数据本身的相位信息丢失, 因此可以从高阶双谱中提取子波的振幅谱和相位谱, 从而重构子波。这种方法规避了传统二阶统计方法的缺点, 能够提取一个准确的子波。基于高阶双谱来提取子波, 不仅仅可以用到反演当中, 还可以进行俞氏子波整形, 能够有效地提高地震资料的纵向分辨率, 有助于对剖面中的薄层进行合理解释。

所以, 基于高阶双谱的子波整形具有很高的实用性, 高阶双谱得到一个准确的地震子波, 再利用这个较为准确的地震子波和目标俞氏子波就可以得到一个好的子波整形效果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ulrych T J, Velis D R, Scacchi M D. Wavelet estimation revisited[J]. The Leading Edge, 1995, 14(11): 1139-1142. [本文引用:1]
[2]	杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-127. [本文引用:1]
[3]	梁光河. 地震子波提取方法研究[J]. 石油物探, 1998, 37(1): 31-39. [本文引用:1]
[4]	Connolly P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. [本文引用:1]
[5]	蔡希玲. 俞氏子波在地震数据处理中的应用研究[J]. 石油地球物理勘探, 2000, 35(4): 497-507. [本文引用:1]
[6]	朱宝山, 燕利芳, 巨朝晖, 等. 俞氏子波整形反褶积在提高地震资料分辨率中的研究与应用[J]. 工程勘察, 2014(2): 92-98 [本文引用:1]
[7]	Lazear G D. Mixed phase wavelet estimation using fourth order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. [本文引用:1]
[8]	Velis D R, Ulrych T J. Simulated annealing wavelet estimation via forth order cumulant matching[J]. Geophysics, 1996, 61(6): 1939-1948. [本文引用:1]
[9]	Matsuoka T, Ulrych T J. Phase estimation using the bispetrum[J]. Proceedings of IEEE, 1984, 72(10): 1403-1411. [本文引用:1]
[10]	张贤达. 时间序列分析——高阶统计量方法[M]. 北京: 清华大学出版社, 1999. [本文引用:1]
[11]	海洋. 基于随机建模的贝叶斯波阻抗反演研究及其在储层预测中的应用[D]. 武汉: 中国地质大学, 2010 [本文引用:2]
[12]	黄建英, 李录名, 罗省贤. 基于高阶谱的地震子波估计[J]. 成都理工大学学报: 自然科学版, 2006, 33(2): 188-192. [本文引用:1]
[13]	Sundaramoorth G, Raghuveer M R, Dianat S A. Bispectral reconstruction of signals in noise: amplitude reconstruction issues[J]. IEEE Trans. Acoustics Speech, Signal Processing, 1990, 38: 1297-1306. [本文引用:1]
[14]	李亚峻, 李月, 高颖. 基于双谱幅值和相位重构的地震子波提取[J]. 地球物理学进展, 2007, 22(3): 947-952. [本文引用:1]
[15]	王西文, 高静怀, 李幼铭. 高分辨率地震资料处理中导数小波函数的构造[J]. 石油物探, 2000, 39(2): 64-71. [本文引用:1]
[16]	张海燕, 李庆忠. 几种常用解析子波的特性分析[J]. 石油地球物理勘探, 2007, 42(6): 651-657. [本文引用:1]
[17]	崔庆辉, 芮拥军, 尚新民, 等. 混合相位地震子波提取及应用[J]. 石油物探, 2011, 50(5): 481-486. [本文引用:1]
[18]	孟大江, 王德利. 基于高阶统计复倒谱子波提取[J]. 物探与化探, 2013, 37(3): 494-499, 511. [本文引用:1]
[19]	Yu Y C, Wang S X, Yuan S Y, et al. Phase estimation in bispectral domain based on conformal mapping and applications in seismic wavelet estimation[J]. Applied Geophysics, 2011, 8(1): 36-47. [本文引用:1]
[20]	张, 曹思远, 郑晓东, 等. 基于高阶统计的时变子波估计及其应用[J]. 物探与化探, 2014, 38(5): 989-995. [本文引用:1]
[21]	高少武, 赵波, 贺振华, 等. 地震子波提取方法研究进展[J]. 地球物理学进展, 2009, 24(4): 1384-1391. [本文引用:1]

1995

0.0

... 准确的子波估计是地震资料反褶积处理、偏移、特征提取、波阻抗反演、地震资料解释和地震正演模型的基础^[1] ...

2008

0.0

杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-127.

地震子波提取方法总体上可分为确定性子波提取方法、统计性子波提取方法两大类。确定性子波提取方法不需要对反射系数序列的分布作任何假设，能得到较为准确的子波，但很容易受各种测井误差的影响，尤其是声波测井资料不准而引起的速度误差会导致子波振幅畸变和相位谱扭曲；统计性子波提取不需要测井信息，也可以得到子波的估计，但需要对地震资料和地下反射系数序列的分布进行某种假设，所得到子波精度与假设条件的满足程度有关。文中对确定性子波提取方法和统计性子波提取方法进行了详尽的评述，并认为可将通信工程中的子空间分解法的思想用于混合相位子波提取。子空间法混合相位子波提取基于信号和噪声子空间正交的原理，建立二次型的目标函数，不需要对地层反射系数做任何假设，因此子波提取准确度高且稳定性好。

... 对于经典的子波提取方法(自相关法、希尔伯特变换法)^[2,3],它们都是基于子波为最小相位假设和噪声为高斯白噪声假设 ...

1998

0.0

梁光河. 地震子波提取方法研究[J]. 石油物探, 1998, 37(1): 31-39.

摘　要：地震子波的提取是波阻抗反演及正演模型的基础工作，本文首先研究了确定性子波提了方法所存在的问题，即子波长度的确定、截断误差的影响，直流分量的消除及随机噪音的影响；然后对最近发展起来的利用地震记录的高阶累积量估算地震子波的方法进行了理论分析，将上述确定性方法和统计性方法结合起来，发展了一种约束外推地震子波的新方法，最后用实际资料进行了试算。

... 对于经典的子波提取方法(自相关法、希尔伯特变换法)^[2,3],它们都是基于子波为最小相位假设和噪声为高斯白噪声假设 ...

1999

0.0

... 研究表明,实际地震资料的地震子波大部分是混合相位的^[4],这违背了经典算法的基本假设,所以根据经典算法提取的子波也是不准确的 ...

2000

0.0

蔡希玲. 俞氏子波在地震数据处理中的应用研究[J]. 石油地球物理勘探, 2000, 35(4): 497-507.

Yu wavelet is a new wavelet that was designed by Professor Yu Shoupeng. It is characterized by narrow main lobe，low side-lobe amplitude，simple waveform，smooth and continuous amplitude spectrum，and so on;so it is a satisfactory wavelet in present high resolution processing. Its construction and characteristics are reviewed in brief ; and its applications in seismic data processing are summarized as follows:.Yu wavelet，the expected output of wavelet deconvolution，may improve deconvolution effect.·The peak frequency of Yu wavelet is adjustable，and its filtering effect is better than that of bandpass filtering..Yu wavelet with peak frequency ameliorates the accuracy of velocity analysis..Yu wavelet may be used to improve the fidelity of synthetic seismogram.·Three practical methods for analysing Yu wavelet parameters are recommended here to facilitate the use of Yu wavelet.It is shown in practice that Yu wavelet has brought good application effect in real data processing.

俞氏子波是由俞寿朋教授提出的一种新型子波 ,它具有主瓣窄、旁瓣幅度小、波形简单、振幅谱光滑连续等特点 ,是目前条件下高分辨率处理中的理想子波。本文简要回顾了俞氏子波的构成及其性质 ,并对它在地震数据处理方面的应用进行了探索 ,即俞氏子波作为子波反褶积的期望输出 ,可以改善反褶积的效果 ;俞氏子波的峰值频率可调 ,它的滤波效果优于带通滤波 ;选择高峰值频率的俞氏子波 ,可提高速度分析的精度 ;俞氏子波用于合成记录 ,可提高其保真度。本文还列举了三种实用的俞氏子波参数分析方法 ,为俞氏子波的使用提供了方便。实践表明 ,俞氏子波在实际数据处理中取得了良好的应用效果。

... 提取子波的一个重要用途就是进行子波整形处理^[5,6],以此来提高地震资料的分辨率 ...

0.0

... 提取子波的一个重要用途就是进行子波整形处理^[5,6],以此来提高地震资料的分辨率 ...

1993

0.0

... 基于高阶统计量的基本理论,利用高阶双谱估算子波的振幅谱和相位谱,最终重构一个准确的子波^[7,8] ...

1996

0.0

... 基于高阶统计量的基本理论,利用高阶双谱估算子波的振幅谱和相位谱,最终重构一个准确的子波^[7,8] ...

1984

0.0

... 由此可见,高阶统计量可以提取混合相位子波^[9] ...

1999

0.0

... 地震记录y(n)的三阶相关函数,即三阶统计量^[10]可近似表示为 ...

2010

0.0

海洋. 基于随机建模的贝叶斯波阻抗反演研究及其在储层预测中的应用[D]. 武汉: 中国地质大学, 2010

随着油气田勘探开发难度的不断增大，油气田开发过程中的精细油气储层预测显得越来越重要。在这一背景下，精细油气储层的预测方法得到了不断的发展和完善。这些方法对于寻找新的开发目标极为关键，它们为油气田的勘探开发提供有力的保证。　　储层预测是一种综合运用地震、地质、测井等基础资料，并以三维地震资料为预测主体，定量预测储层的空间几何形态及物性参数在空间的分布特征的技术。目前，油气储层预测常用的方法有波形振幅法、波阻抗反演法和频谱分析法等等。其中，波阻抗反演是最有效的储层预测方法。但是，波阻抗反演方法至今还存在很多技术问...

... 为方差,且是一个常数,通常取1^[11] ...

... 是满秩的矩阵,故可以得到^[11] ...

2006

0.0

黄建英, 李录名, 罗省贤. 基于高阶谱的地震子波估计[J]. 成都理工大学学报: 自然科学版, 2006, 33(2): 188-192.

常规的地震子波估计是在假设子波为最小相位的基础上对地震记录进行处理.针对这一局限性,研究了基于地震记录高阶谱的地震子波估计方法.该方法无需对子波作任何假设,直接从地震记录的高阶谱中恢复地震子波的振幅谱和相位谱,进而重构地震子波,并对不同相位地震子波的理论模型和野外实际资料进行了处理,结果表明这一方法对于提高地震资料的分辨率具有可行性和应用潜力.

... 同时,可以得到地震子波高阶双谱的振幅谱和相位谱^[12],分别是 ...

1990

0.0

... 2 子波的振幅重构通过地震子波的双谱重构地震子波振幅的方法有很多(如递推算法、最小二乘法和DFT法),其中最小二乘法能够有效避免其他方法中误差传递的缺点,因此笔者采用经典的最小二乘算法来完成^[13] ...

2007

0.0

李亚峻, 李月, 高颖. 基于双谱幅值和相位重构的地震子波提取[J]. 地球物理学进展, 2007, 22(3): 947-952.

This paper is based on the fact that bispectrum of seismic signals contains amplitude and phase information of seismic wavelet, also has strong anti-noise-interference ability besides. A method of extracting wavelet using bispectrum amplitude and phase reconstruction is introduced in this paper. After extracting amplitude and phase information of wavelet, one can completely reconstruct seismic wavelet by inverse Fourier transform. A new method on choosing the initial value for recursion formula of bispectrum phase reconstruction has improved the wavelet estimation stability. The feasibility of the method is demonstrated by the simulation testing.

利用地震记录双谱中包含子波的幅值和相位信息，以及其超强的抗噪声干扰能力，采用一种基于双谱幅值和相位重构的地震子波提取方法，首先提取出子波幅值及相位信息，进而通过傅立叶反变换，使子波得以完全恢复.本文针对双谱相位重构递推公式，提出一种新的初值选取方法，使地震子波估计的稳定性得到了提高.仿真实验证实了该方法的可行性.

... 其中W'就是求得的子波振幅谱的对数谱^[14],求其反对数,由其对称性就可以得到地震子波的振幅谱,即 ...

2000

0.0

王西文, 高静怀, 李幼铭. 高分辨率地震资料处理中导数小波函数的构造[J]. 石油物探, 2000, 39(2): 64-71.

基于地震子波的模拟公式,可以很好地模拟零相位和混合相位子波,在一定意义上也可以近似模拟最大相位及最小相位子波.模拟出的子波再加上适当的修正项后满足允许条件,可作为小波函数.基于改进的Morlet小波,推导出导数小波函数,能更好地适应于地震资料处理.根据构造出的各种小波函数在时间-尺度域对信号的展开特征,导数小波函数作为基本小波,可以对地震资料进行高分辨分频处理和瞬时特征提取.最后,应用实例证明了构造导数小波函数的有效性和合理性.

... 2 仿真实验根据褶积模型,利用改进的Morlet子波^[15]得到混合相位子波 ...

2007

0.0

张海燕, 李庆忠. 几种常用解析子波的特性分析[J]. 石油地球物理勘探, 2007, 42(6): 651-657.

本文通过对几种常见解析子波的数学表达式及相应波形和振幅谱的分析，阐述了它们的主要特点和适用范围，并首次介绍了最适于表达实际爆炸地震子波的阻尼拉伸正弦子波——李子波。文中着重强调了在选用带通子波进行带通滤波时，应采用频域归一化的滤波算子才能获得较好的振幅保持特性。比较宽带雷克子波和雷克子波的不同特征可知，子波分辨率的高低主要取决于主瓣的宽度和主瓣范围内的瞬时频率的高低，而与峰值频率没有关系。近似为最小相位的阻尼拉伸正弦子波——李子波，可应用于满足最小相位假设的反褶积等处理运算。

... 利用上述方法统计子波,并将所统计的混合相位子波整形为俞氏宽频子波^[16],进而实现子波整形 ...

2011

0.0

2013

0.0

孟大江, 王德利. 基于高阶统计复倒谱子波提取[J]. 物探与化探, 2013, 37(3): 494-499, 511.

Wavelet deconvolution is one of the main methods to improve the resolution of seismic data,and the key is the accuracy of the wavelet.Conventional methods usually presume that the wavelet is the minimum phase,but this may not be correct.To solve this problem,the authors utilized the property of the higher order statistic quantity that it includes phase information of the system and suppresses Gaussian noise to study the wavelet extraction method based on cepstrum and, as a result,gave the principles of extracted wavelet based on complex cepstrum,bispectrum and trispectra.In addition the authors constructed a smooth window function to improve the accuracy of wavelet.The method does not need to make any assumption about wavelet's phase,and it can extract wavelet of any phase.Tackling the mixed wavelet,the authors made theoretical experiments to verify the effectiveness of the method,and the results of actual data processing showed the effectiveness of the method.

子波反褶积是提高地震资料分辨率的主要方法之一,其关键在于子波的准确性。常规处理方法通常假设子波是最小相位的,但这是不符合实际的,针对这一局限性,利用高阶统计量包含系统相位信息以及抑制高斯噪声的特性,研究了基于复倒谱子波提取方法,分别给出了复倒双谱和复倒三谱提取子波的原理,并构造了平滑窗函数来提高子波估计的准确性。该方法无需对子波相位作任何假设,可估计任意相位子波。针对混合相位子波,进行了理论试算,验证了该方法的有效性,最后对实际资料处理的结果也说明了该方法的实际应用价值。

2011

0.0

2014

0.0

张, 曹思远, 郑晓东, 等. 基于高阶统计的时变子波估计及其应用[J]. 物探与化探, 2014, 38(5): 989-995.

Wavelet estimation is the foundation of high-resolution seismic data processing and interpretation. It is of great significance to estimate the wavelet rapidly and exactly. This paper gets the amplitude spectrum from the trispetrum and phase from the seismic data based on the principle of kurtosis maximum, which avoids phase wrapping properly, and discusses the application condition of this principle. The property of the different window functions is also compared, and Hamming is moved to calculate the time-varying wavelets. The ricker wavlet model is used which is frequency-changing to illustrate its effectiveness. In the real data processing, the method is comparatively analyzed for the well-seismic calibrated data based on different frequency ricker wavlets. The results show that the estimated wavlet amplitude spectrum is more stable, and the phase spectrum can be realized easily and is more consistent with the true wavelet.

地震子波估计是地震资料高分辨处理、解释的基础，快速准确地估计地震子波具有重要意义。笔者利用三谱估计子波的振幅谱，根据峰度最大值准则提取子波的相位，规避了相位的卷绕问题，并讨论了该准则的适用条件。比较了不同窗函数的特性，最终选定Hamming窗函数滑动求取时变子波。利用变频雷克子波模型讨论了时变子波提取的有效性。应用到实际资料处理中，与不同主频的雷克子波标定的地震记录进行对比分析。结果表明：该方法使得子波振幅谱估计更加稳定，相位谱估计更易于实现，与实际情况更加符合。

2009

0.0

高少武, 赵波, 贺振华, 等. 地震子波提取方法研究进展[J]. 地球物理学进展, 2009, 24(4): 1384-1391.

Wavelet extraction of seismic data is a basic task in the processing of seismic data deconvolution, impedance inversion and forward modeling． For the seismic data processing of high resolution, high signal-to-noise ratio and high fidelity, it has an extreme significance to estimate seismic wavelet accurately． Over the past twenty years, theories and techniques in digital signal processing, non-linear sciences and optimization have made great development, and their uses come down to the seismic data processing, at the same time it gives great impetus to the development of the technique and method of the seismic wavelet extraction． In this paper, we first briefly explain the convolution model with the closest relation to the seismic wavelet, then we give a summary of seismic wavelet extraction. Finally we simply discuss the prospect of the seismic wavelet extraction．

地震数据子波提取，是地震资料反褶积处理、波阻抗反演以及正演模拟的基础工作．准确的地震子波估计技术对于高分辨率、高信噪比、高保真度的地震勘探数据处理具有极为重要的意义．在过去的二三十年中，数字信号处理理论、非线性理论、优化理论得到了很大发展，这些为地震子波提取技术和方法注入了新的巨大活力．本文首先简要地说明了与地震子波紧密相关的褶积模型，然后对地震子波提取现状进行了概括阐述，最后给出了地震子波提取前景展望．