小波基函数是通过小波母函数平移伸缩后得到的。小波母函数ψ (t)∈ L²(R), 其傅里叶变换 ψ˙(w)满足容许性条件:

Cψ=∫-∞+∞ψ˙(w)|2w-1dw< ∞。

若对小波ψ (t)进行平移、伸缩, 即可得到小波基函数的集合{ψ _{a, b}(t)}:

ψa, b(t)=a-12ψt-ba,

其中:a、b∈ R, a> 0。a为尺度因子, 它反映一个具体的基函数的伸缩尺度, a越小, 则小波越窄。b为平移因子, 指明函数随t轴平移的位置; ψ _{a, b}(t)的中心位于t=b处。当a=2^j, b=n× 2^k, 其中j、k∈ Z, 得到离散小波函数为

ψj, k(t)=a-j2ψ(2-jt-k), j、k∈Z。

小波多尺度分析方法是通过选取小波基对重力异常场进行小波变换, 将重力异常场分解成许多小尺度异常, 再根据地质目的组合部分小尺度异常, 并对组合后异常进行分析的一种方法。异常场是指地下不同深度层次、形态、规模的地质体引起的异常的叠加, 并包含不同程度的噪声。一般情况下, 深部地质体引起的异常特征比较平缓, 以低频成分为主, 浅部地质体所引起的异常特征变化比较剧烈, 以中、高频成分为主, 噪声多为高频扰动, 小尺度局部异常特征往往叠加在异常场上。通过多尺度分析, 将异常信号分解成不同频带, 并结合异常特征进行局部场和区域场^[15]的分离以及噪音的消除处理。

区域场的分离主要是利用离散小波变换进行, 通过多尺度分析mallat算法^{[16, 17, 18]}, 得到异常场的各阶细节和逼近。设重力数据的矩阵为D, 经n阶(n为整数, n≥ 2)离散小波变换后产生小波细节D₁, D₂, …, D_n-1, D_n和n阶逼近S_n, 其间小波细节不随n的增大而改变。若将重力场进行二分, 最后分解得到的重力区域场为S_n, 重力局部异常场为D₁+D₂+…+D_n。

通常情况下, 小波基函数的选择需要考虑4个因素^{[14, 19]}:正则性、正交性、支撑宽度和消失矩阶数。正则性, 即小波基函数的光滑程度, 决定了最小化量化误差; 正则性越好, 滤掉的图像细节越多, 正则性越差, 滤波器处理效果越恶化。正交性和对称性有利于小波系数分解后的精确重构, 避免信号在多尺度分解重构后失真。支撑宽度是从时间复杂的角度考虑的, 小波变换为一个卷积的过程, 卷积核不宜太长, 否则会严重影响运算的时间。消失矩和正则性相关联, 消失距越大, 对应的小波滤波器就越平坦, 小波函数的震荡也越强, 越大的消失距将使高频系数越小, 图像能量也就越集中, 压缩性更好。通常情况下消失距大些比较适用。表1为笔者所要研究的5种常用小波簇的主要特征。

表1

表1

表1 5种小波簇的主要特征 小波簇 正交性 紧支撑性 对称性 支撑宽度 消失矩阶数 haar 有 有 对称 1 1 dbN 有 有 近似对称 2N+1 N biorNr.Nd 无 有 不对称 重构2Nr+1 Nr-1 分解2Nd+1 coifN 有 有 近似对称 6N-1 2N symN 有 有 近似对称 2N-1 N 注:N— 阶数; Nr— Bior小波的重构阶数; Nd— Bior小波的分解小波基的阶数

表1 5种小波簇的主要特征

根据重力场异常是由局部场异常(细节异常)和区域场异常(逼近异常)叠加而成, 笔者分别对每一个小波簇进行一维模型对比试验。使用同一簇的所有小波基函数分别对一维重力异常模型进行多尺度分解, 将分解得到的逼近异常S_n与模型正演异常进行比对, 求取相关系数。系数越接近1, 相似度越大, 即选取的小波基对一维重力场异常的分解则更为精确。由于小波基函数是通过母函数伸缩平移得到的, 同一个小波簇中的各个小波基性质最为相似, 即可通过一维模型试验得到各簇小波基中的最优小波基。

不同簇小波基性质相差较大, 对相同二维重力数据的成像能力不同。文中使用一维模型试验得到的各簇最优小波基, 进行二维重力模型对比试验, 并同时对华北地区实测布格重力异常数据进行试验, 比较其数据处理后的成像好坏, 选出适合重力多尺度分析的最优小波基。

表2

表2

表2 dbN小波簇处理结果相关系数 小波基 db1 db2 db3 db4 db5 db6 db7 db8 db9 相关系数 0.75282 0.72562 0.93285 0.89870 0.96431 0.95136 0.99086 0.96283 0.99460 小波基 Db10 Db11 Db12 Db13 Db14 Db15 Db16 Db17 Db18 相关系数 0.97800 0.99740 0.97594 0.99690 0.96363 0.99620 0.98042 0.99707 0.94339

表2 dbN小波簇处理结果相关系数

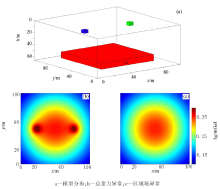
根据试验目的所设计的地质体模型如图1b所示, 异常曲线见图1a。地质体m1和m2的长度均为5 m, 埋深均为5~10 m, 剩余密度Δ σ ₁=1 000 kg/m³, Δ σ ₂=900 kg/m³, 正演得到的异常表示浅层局部场重力异常的叠加; 地质体m3长67.2 m, 埋深50~60 m, 剩余密度Δ σ ₃=500 kg/m³, 正演得到的异常表示深层的区域场重力异常。

图1

	Figure Option ViewDownloadNew Window
	图1 一维重力异常理论模型

该模型为简单2层模型, 经小波多尺度分解可得到一个由深层地质体m3引起的逼近异常和一个由浅层地质体m1、m2引起的叠加细节异常。以dbN簇小波为例, 使用簇中的所有小波基对该模型进行多尺度分解, 将得到的逼近异常曲线S_n与深层地质体m3正演异常曲线进行对比, 求取相关系数(表2), 选出系数最接近1的小波基作为该簇的最优小波基。

实验结果(表2)表明:在dbN小波簇中, N小于5的小波基正则性差, 光滑度不够, 得到的相关系数小; 随着N的增大, 正则性变好, 光滑度得到了保证, 相关系数更加接近1; N大于12以后, 支撑宽度增大导致小波局部特性变差, 相关系数下降。综合考虑, db11小波基为dbN簇的最优小波基。通过同样的分析方法选出了其他小波簇的最优小波基, 分别为bior6.8, sym8和coif5。

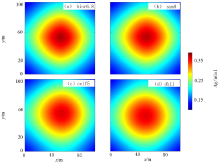
为了观察各簇最优小波基对二维数据的处理成像能力, 将一维模型的3个地质体在x-y面上延展成为正方形, 如图2a所示, 正演得到总重力异常(图2b)以及区域场异常(图2c)。

图2

	Figure Option ViewDownloadNew Window
	图2 二维理论模型

分别用db11、bior6.8、sym8和coif5小波基对二维模型正演总异常进行多尺度分解, 得到4个逼近重力异常(图3)。对比结果表明, 4个逼近异常的形态由中心的同心圆向边界的棱形转变, 使用bior6.8小波基分解得到的逼近异常中心场值最大。

图3

	Figure Option ViewDownloadNew Window
	图3 逼近重力异常

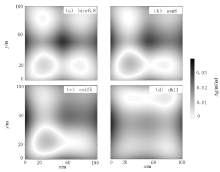
为了更加直观地观察小波基处理结果, 将分解得到的二维逼近重力异常(图3)与理论逼近异常(图2c)进行差值运算, 得到区域场异常相对误差E_误差(图4), E_误差的范围在0~0.04 mGal。各小波基处理结果的误差大小及水平偏移情况由图4所示, 结果表明, sym8小波基(图4b)和coif5小波基(图4c)分解得到的逼近异常左下角误差较大, 在对角线方向上, 逼近异常峰值位置发生了较大偏移。相比较, bior6.8小波基(图4a)和db11小波基(图4d)分解得到的逼近异常比较对称, 峰值位置偏移较小, 表明bior6.8和db11应优于sym8和coif5小波基。从异常值大小方面来考虑, db11小波基处理得到的异常中心位置异常值大小比bior6.8处理得到的要精确, 但异常中心四周的异常值大小比bior6.8得到的误差要大。

图4

	Figure Option ViewDownloadNew Window
	图4 区域场异常相对误差

引用统计学中均方差理论, 计算得到相对误差E_误差的均值μ _误差和均方差σ _误差, 如表3所示。μ _误差反映小波基处理得到的区域场异常数值的准确性, μ _误差越小, 区域场异常数值越精准; σ _误差反映误差的一致性, 即区域场异常曲面在水平面上的偏移程度, σ _误差越小, 异常曲面水平方位越准确。对比数据得出, db11小波基处理结果误差最小, 误差一致性最好。

表3

表3

表3 各小波基处理结果误差的均值μ 误差和均方差σ 误差 小波基 Bior6.8 Sym8 Coif5 db11 μ 误差/10-2 1.1827 1.2364 1.3423 1.1711 σ 误差/10-5 5.1932 5.0092 4.7832 3.866

表3 各小波基处理结果误差的均值μ 误差和均方差σ 误差

模型试验表明, db11小波基最优, 在实际数据试验中, 通过db11小波基与bior6.8小波基的对比, 进一步判断db11小波基的实用性。

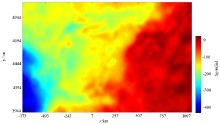
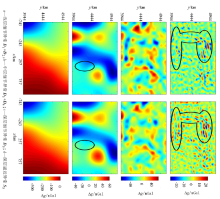
为了判断db11和bior6.8小波基处理结果的优劣, 进行实测数据对比试验, 实测数据为华北测区布格重力异常数据(图5)。测区地理范围为东经102° ~123° , 北纬32° 30'~42° 30', 采用兰勃特等角割圆锥投影, 中央经线为110° , 第一标准纬线为34° , 第二标准纬线为44° , 零点纬线为赤道(0° 纬线)。网格数据坐标范围为东西向-743~1 062 km, 南北向3 944~5 094 km。分别使用db11小波基和bior6.8小波基对华北地区布格重力异常进行5层分解, 得到5个细节异常和1个逼近异常, 经过一定的组合后, 得到浅层细节异常D₁+D₂、中层细节异常D₃+D₄、深层细节异常D₅以及深层逼近异常S₅(图6)。

图5

	Figure Option ViewDownloadNew Window
	图5 华北测区布格重力异常

图6

	Figure Option ViewDownloadNew Window
	图6 华北地区布格重力异常bior6.8小波基(左), db11小波基(右)5层分解成果

结合已有的地质背景资料对分解结果图进行分析。浅层细节异常D₁+D₂对应沉积盆地中的地层以及造山带或隆起区近地表侵入体, db11小波基处理得到D₁+D₂细节更为突出, 侵入体易被识别(已用黑线圈出); 深层细节异常D₅主要对应上地壳底部与中地壳岩石密度的变化, db11小波基处理得到轮廓刻画更为准确(已用黑线圈出); 中层细节异常D₃+D₄主要对应上地壳的结晶基底, 深层逼近异常S₅反映的主要是莫霍面起伏以及下地壳岩石密度变化, 两小波基处理结果相近, 偏差不大。

db11小波基为正交近似对称小波基, 消失矩阶数为11, 而Bior6.8小波基为非正交非对称小波基, 消失矩阶数只有5, 这使得bior6.8小波基在多尺度分解重构中丢失部分细节, 数据成像以及大尺度数据细节处理能力不如db11小波基。综合比较, db11小波基较bior6.8小波基更适合用于重力数据处理, db11小波基为最优小波基。