引用本文
王琦标, 蒋鑫, 庹先国, 毛小波, 李怀良. 西藏甲玛铜多金属矿储量估算的新方法[J]. 物探与化探, 2015,39(5): 1001-1007.
WANG Qi-biao, JIANG Xin, TUO Xian-Guo, MAO Xiao-Bo, LI Huai-Liang. A new resource estimation method for the Jiama polymetallic copper deposit in Tibet[J]. Geophysical and Geochemical Exploration, 2015,39(5): 1001-1007.
Doi:10.11720/wtyht.2015.5.20  
Permissions
Copyright©2015, 物探与化探编辑部
《物探与化探》编辑部
西藏甲玛铜多金属矿储量估算的新方法
王琦标1, 蒋鑫1, 庹先国1,2, 毛小波1, 李怀良2
1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059
2.西南科技大学 核废物与环境安全国防重点学科实验室,四川 绵阳 621010

作者简介: 王琦标(1991-),男,汉族,江西人,硕士研究生,研究方向为核地球物理,现主要从事勘探设备软件开发工作。

收稿日期: 2014-06-03
基金: 国家自然科学基金重大科研仪器设备研制专项(41227802); 国家杰出青年基金(41025015)
摘要

西藏甲玛铜多金属矿的钻孔分析数据多呈条带状分布,采用协同克里格法对这种条带状数据进行插值时,易出现端点数据权值偏大的情况。笔者介绍了协同克里格算法的相关理论,以此为基础,对端点数据的权值进行校正,使越远的数据点权值越小,并且给出了校正算法的程序代码。以2012年甲玛矿区勘探工程的Cu含量数据为例,分别进行了协同克里格法插值和权值校正的协同克里格法插值,实验结果表明,权值校正的协同克里格法能取得更为良好的效果,对于西藏甲玛铜多金属矿的地质属性、储量估算等空间数据建模具有重要意义。

关键词: 储量估算; 协同克里格法; 条带状分布; 权值校正; 西藏甲玛铜多金属矿
中图分类号:P632 文献标志码:A 文章编号:1000-8918(2015)05-1001-07 doi: 10.11720/wtyht.2015.5.20
A new resource estimation method for the Jiama polymetallic copper deposit in Tibet
WANG Qi-biao1, JIANG Xin1, TUO Xian-Guo1,2, MAO Xiao-Bo1, LI Huai-Liang2
1. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China
2. Key Laboratory for Radioactive Waste and Environmental Security, Southwest University of Science and Technology, Mianyang 621010, China
Abstract

The analytical data of drill holes from the Jiama polymetallic copper deposit exhibit striped distribution. When Cokriging is used for these striped data, the outlying data in the stripe frequently receive higher weights than all other data. This paper first introduced the relevant theory of Cokriging algorithm, then corrected the weight of outlying data in the stripe based on Cokriging algorithm with the purpose of making outlying data receive smaller weights, and finally presented the program of the correction algorithm. With the grade data of Cu in the Jiama ore district obtained in 2012 as an example, the authors calculated Cokriging and Cokriging of weight correction respectively. The results show that the Cokriging of weight correction can achieve the better effect and hence it is important for the modeling of geological properties, reserves estimation and spatial data of the Jiama polymetallic copper deposit in Tibet.

Keyword: reserves estimation; Cokriging; striped distribution; weight correction; the Jiama polymetallic copper deposit in Tibet

西藏墨竹工卡县甲玛矽卡岩— 角岩型铜多金属矿床是目前我国同类矿床矿石品质最好、成矿元素多、探明的资源量已经达到超大型规模的矿床[1]。对于该地区的储量估算采用过传统断面法[2]、SD法[3]和地质统计学方法[4], 其中协同克里格法(地质统计学方法中的一种)最能反映该地区多种金属之间的协同区域化[5]现象。

但是, 西藏甲玛铜多金属矿所处区域内的地层比较复杂, 地层曲面变化较大, 甚至可能存在地层曲面相交和错断的情况。因此, 运用协同克里格法计算储量时, 会出现钻孔数据采样不均、呈条带状分布 611的情况, 即有限的条带两端数据权值偏大, 导致插值结果不合理。在这种情况下, 笔者采用拟牛顿法[12]对协同克里格插值得到的权值进行校正, 在估值方差基本不变的前提下使协同克里格估值的权值更为合理, 并且以西藏甲玛铜多金属矿的储量估算为实例对该方法进行了验证。

1 协同克里格算法原理

在用协同克里格法 1318进行储量估算时, 对于由K个变量构成的协同区域化变量Zk(x), k=1, 2, …, K, 有相邻m个位于位置ui=(i=1, 2, …, m)处的数据点, 将中心点的品位数据设为Z(uk, i), i=1, …, m; k=1, …, K; K为协同区域化变量个数。在待估点Z(u0)处的协同克里格的估计量为

其中λ k, i是第k个区域化变量中的第i个样本点权值, 由最小化方差求出

σu02=E{Z(u0)-Z* (u0)}2→min。(2)

设样品数据点ui(i=1, 2, …, m)与待估点u0之间的距离为di, 则式(2)的最小化问题中的权值有如下约束:

2 钻孔条带状效应分析

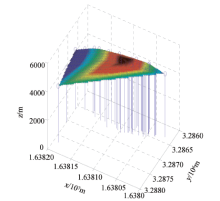
西藏甲玛铜多金属矿最主要的数据来源是沿着钻孔获取到的数据, 其中包括地面钻孔数据、钻孔化验数据、小体重数据等。原始数据为截止到2012年甲玛矿区勘探工程得到的数据, 包括58个钻孔, 共计15 187件化学样。矿床地表模型及钻孔点的三维模型如图1所示。

图1 地表及钻孔点三维模型

图2 数据被断层边界截断

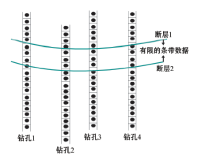
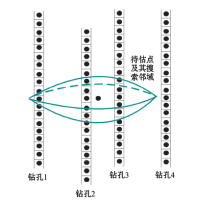
如果某一个钻孔遇到地层的错断情况, 钻孔数据就会出现边界截断, 如图2所示。另外如图3所示, 在进行协同克里格插值时首先会确定一个搜索范围, 该范围在三维空间内通常为一个椭球体的边界截断。这两种现象称之为钻孔的有限条带状数据。

图3 数据被搜索邻域截断

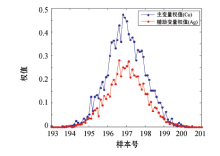
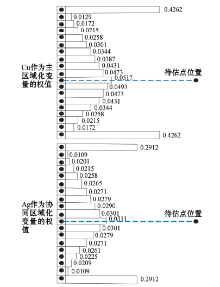
以Cu和Ag协同区域化为例, 对其中一列有限的条带状数据进行协同克里格 1318插值计算。估值计算时Cu和Ag的变差函数以及两种元素的交叉变差函数均采用球状模型, 通过计算可以得到块金效应 1318(表征变差函数原点处的连续性)为0的协同克里格权值系数, 其结果如图4所示。

图4 协同克里格引起的条带状效应

图4显示的这些权值体现了采用协同克里格估值时的条带状效应:对于单个钻孔数据的估值, 待估点离钻孔数据最远的两端, 其样品点所获得的权值异常偏大, 而离待估点较近位置的权值则普遍较小。根据克里格估值方法中的屏蔽效应 1318(即若块金效应为0或很小时, 则在待估区内的样本权系数最大, 稍远一点则其权系数显著减少), 图4显示的权值是不符合实际情况的, 特别是当数据的分布在断层或者搜索范围截出不平稳的数据时, 就会出现端点数据处的权值明显大于或小于中间数据的权值的现象, 所以需要对其进行校正。

3 拟牛顿法权值校正

对权值系数进行约束需要满足式(3)中的最小化问题约束条件。笔者采用拟牛顿法[12], 其流程如图5所示。

图5 拟牛顿法校正权值流程

图中拟牛顿法的计算过程为:为了使距离最近的已知点获得最大的权值, 使最远的已知点获得最小的权值, 首先需要对距离d按升序排列, 然后用协同克里格计算权值, 在第k个区域化变量的权值下, 给定初始迭代值xk, 0。为求最优解xk, 1, 通过下降方向Sp+1=-Hp+1∇f(xk, p+1)得到迭代公式xk, p+1=xk, p+Sp, 其中p为迭代次数, f函数为最小化方差计算公式。如式(2)所示, 当∇f(xk, p+1)的范数达到给定的控制误差时, xk, 1=xk, p+1即为最优解, Hp+1可通过如下计算公式求得:

Hp+1=Hp-HpypypTHpypTHpyp+SpSpTypTSp。(4)

其中yp=∇f(xk, p+1)-∇f(xk, p), Sp=xk, p+1-xk, p, 计算时的第一步迭代取H1=I(单位矩阵)。

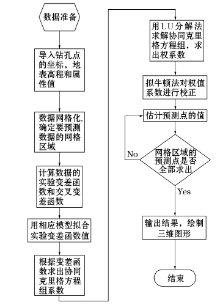
权值校正之后的协同克里格算法流程如图6所示。

图6 权值校正协同克里格插值算法流程

4 处理结果
4.1 数据预处理

采用权值校正协同克里格法估计矿床储量, 首先要选取区域化变量。区域化变量必须具备随机性和结构性的双重性质, 即在受限的地质范围内既要具有一定的相关性又要具有随机变化的统计特征。由于甲玛矿床是 Cu、Mo、Au、Ag、Pb、Zn 等的复合多金属矿床, 并且有大量的钻孔化验数据, 所以选取金属元素的含量作为区域化变量。本次采用 Cu 含量数据来进行说明。

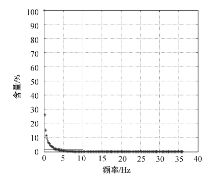
在矿产储量和品位计算之前, 先对钻孔数据进行预处理, 包括特异值处理与样品组合处理。首先根据 Cu的含量数据, 在正态概率纸上作累积频率曲线(图7)。从图上可以看出, Cu含量累积频率曲线总体上为一直线, 表明数据基本符合正态分布。

图7 甲玛矿床Cu含量累积频率曲线

在直线上部存在少量离散点, 且偏离直线方向, 这种离散点才是真正的特异值。

本次估算采用频率曲线法进行特高品位代替, 即将曲线发生偏离直线方向处的含量值取为上截品位, 将所有高于上截品位的含量数据全部用上截品位值替代。笔者取1.5%为上截品位, 矿区Cu含量高于1.5%的样品共有782个, 替代率为5.15%。如果不对这782个样品含量进行替代, 将会出现权值普遍偏大的情况, 导致插值结果不合理。替代前、后的统计分析见表1。

表1 甲玛矿床Cu特异值处理结果

甲玛矿区化学样的样长多为 1 m 或 2 m, 样品长度各不相同。在利用权值校正协同克里格方法进行资源量估算时, 要求所有参与计算的样品具有相同的样长, 即需要进行样品组合。理论上, 组合样品的长度最好与实际采矿台阶的高度一致。甲玛矿区实际采矿台阶高度为10 m, 但考虑到该矿床为矽卡岩型多金属矿床, 矿体“ 分枝、复合” 现象比较明显, 而且地下开采部分夹石剔除厚度为 4 m, 露天采矿部分夹石剔除厚度为 8 m, 因此, 取6 m长度作为组合样长, 一方面可把夹石剔除, 另一方面可把小范围内(大于6 m)的变异也反映出来。组合样中Cu特征值的统计结果见表2。

表2 甲玛矿床Cu样品组合处理的统计结果
4.2 协同克里格法储量估算

4.2.1 变差函数及结构分析

对组合样本进行统计分析, 从表3中可以看出, 组合样品中Cu含量数据与Ag含量数据相关程度最大, 所以笔者以Ag作为辅助变量对Cu的品位进行估值。

表3 组合样本中各元素与Cu的相关系数统计

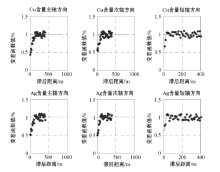
进行权值校正协同克里格法插值的第一步是得到Cu含量和Ag含量的变差函数, 以及两者的交叉变差函数。把所有钻孔点两两组合成点对, 计算其距离值, 再以球状模型拟合理论实验变差函数。Cu、Ag三个变差函数轴的方向定位及其计算结果见表4, 变差函数见图8。

图8 甲玛矿床Cu、Ag变差函数

表4 Cu和Ag变差函数参数

图中所示, 两种元素在各个方向上的变差函数比较相似, 因此推断, 所有变差函数都是各向同性的。对Cu、Ag三个轴方向上的变差函数进行结构套合, Cu品位的变差函数模型为:

γ(h)=0.45+0.5532h100-12h1003;

Ag品位的变差函数模型为:

γ(h)=0.5+0.532h107-12h1073。

以这两种品位为基础计算它们的交叉变差函数, 同样交叉变差函数的变化趋势满足球状模型, 所以用球状模型拟合计算出交叉变差函数的基台值为0.58, 拱高为0.42, 变程为55 m, 其变差函数如图9所示。

图9 甲玛矿床Cu、Ag交叉变差函数

4.2.2 权值校正

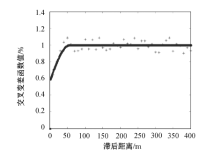
选取钻孔2012jm-8576的条带状数据作为测试数据, 选取钻孔中间位置为待估位置, 将协同克里格方程组求出的权重系数按图5所示的拟牛顿法进行权值校正, 单个钻孔的校正的权值结果如图10所示。钻孔含量数据为294个, 待估样品点的位置在197号样品点附近, 距离待估点附近的权值偏大, 离待估点越远, 权值越小, 符合实际情况。

图10 钻孔2012jm-8576权值校正结果

4.2.3 算法模型验证

为了检验权值校正协同克里格插值的准确性, 采用地质统计学自身完善的交叉验证方法进行验证。基本原理是:从信息样集合中临时抽取一个点作为已知值, 利用权值校正协同克里格插值模型和已知样品去估计这个已知值, 然后把真实值和估计

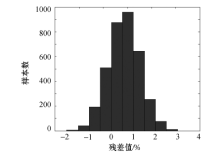
值进行比较, 对两者的残差(差值)进行统计分析, 以判断变差函数结构的正确性。对甲玛矿区样品中Cu含量估值情况进行交叉验证, 结果如图11所示。

图11 Cu含量交叉验证结果

同理用协同克里格插值模型和已知样品去估算已知值, 与权值校正的协同克里格模型相比, 结果如表5所示。

表5 权值校正协同克里格验证结果

通过验证, 残差的分布为正态分布, 各元素含量实际值与估计值之间的均值相当接近, 表明模型确定合理, 变差函数参数对元素含量进行估计是无偏的, 满足区域化变量平稳假设, 能用于下一步的储量计算。与普通的协同克里格模型相比发现, 在3 570个组合样品点上, 权值校正协同克里格插值模型减少了估值的平均误差, 而普通的协同克里格插值模型的标准差总是高于权值校正的协同克里格插值模型的标准差, 表明权值校正协同克里格模型在储量计算方面精度更高。

4.2.4 储量计算

针对三维块段模型的储量计算, 笔者首先考虑甲玛矿区的勘探网度和变差函数的特征, 以确定单元块段的尺寸参数(表6)。

表6 块段估值参数

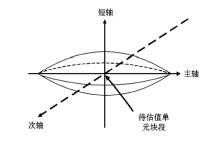
甲玛矿区共划分出153 600个单元块段(以每个坐标轴的最大值减去最小值的距离除以单元尺寸, 得出每个方向的块段数; 每个方向上块段数的乘积为总单元块段), 对每个单元块段的Cu含量进行估值时, 需要确定对于该估值点的搜索范围。由于Cu的变差函数模型以及与辅助变量之间的交叉变差函数模型都呈球状模型变化趋势, 球状模型的特点是:变差函数值随着距离变化到变程时, 变差函数值就稳定为基台值, 所以变程大小直接影响待估单元块段的搜索区域。进行权值校正协同克里格估值时, 将搜索范围定义为具有一个长轴和两个短轴的三维椭球体, 综合Cu球状模型参数和矿区钻孔分布间隔的因素, 搜索的三维椭球体长轴设为200 m, 次轴设为200 m, 短轴设为30 m, 在整个椭球体内部的单元块段都要参与估值计算(图12)。

图12 估值点搜索范围

通过计算, 甲玛矿区共探获矽卡岩型矿体中铜金属量为209万t。

5 结语

对于西藏自治区墨竹工卡县甲码铜多金属矿床储量估算, 当用传统克里格方法进行插值计算时, 没有考虑不同金属元素的相关关系, 并且使用的数据是有限的条带数据, 插值结果会出现条带状效应, 即在单个钻孔之中, 断层外围的数据要比其他位置的数据获得更高的权值。基于此, 笔者以协同克里格法为基础, 以西藏甲码铜多金属矿的钻孔数据资料为依据, 对原始数据进行了预处理、特异值处理、统计分析等, 然后计算Cu、Ag的变差函数及其交叉变差函数, 以构造协同克里格方程组, 通过求解方程组得出权值系数。

笔者着重对发生条带状效应的权值系数进行分析, 提出一种新的估值方法:采用拟牛顿法来对不符合实际情况的权值进行校正处理, 即权值校正的协同克里格方法。最后对甲玛矿区的Cu储量进行了估算, 得到Cu金属量为209万t。同时通过方差验证, 并与普通协同克里格法的验证结果进行对比, 发现权值校正的协同克里格法因为消除了条带状效应的影响, 可靠性更高, 能为矿山开采设计提供科学、可靠的依据。

The authors have declared that no competing interests exist.

参考文献
[1] 黎枫佶. 西藏墨竹工卡县甲玛铜多金属矿三维模型构建和资源量估算[D]. 成都: 成都理工大学, 2010. [本文引用:1]
[2] 施俊法, 唐金荣, 周平, 等. 世界找矿模型与矿产勘查[M]. 北京: 地质出版社, 2010, 1-72. [本文引用:1]
[3] 柳炳利. 基于SD法的固体矿产资源研究[D]. 成都: 成都理工大学, 2009. [本文引用:1]
[4] 程勖. 地质统计学软件开发与应用[D]. 吉林: 吉林大学, 2009. [本文引用:1]
[5] 牛文杰, 孟宪海, 李吉刚. 结合软数据的同位置协同克里金估值新方法[J]. 煤田地质与勘探, 2011, 39(2): 13-17. [本文引用:1]
[6] 李庆谋. 多维分形克里格方法[J]. 地球科学进展, 2005, 20(2): 248-256. [本文引用:1]
[7] 李少华, 王勇标, 李君, 等. 克里金估值中条带效应的校正[J]. 石油地球物理勘探, 2012, 47(6): 979-983. [本文引用:1]
[8] 高美娟, 朱庆忠, 张淑华. 利用贝叶斯—克里金估计技术进行储层参数预测[J]. 石油地球物理勘探, 1999, 34(4): 390-397. [本文引用:1]
[9] 李君, 李少华, 毛平, 等. Kriging插值中条件数据点个数的选择[J]. 断块油气田, 2010, 17(3): 277-279. [本文引用:1]
[10] 汪保, 孙秦. 改进的Kriging模型的可靠度计算[J]. 计算机仿真, 2011, 28(2): 113-116. [本文引用:1]
[11] 牛文杰, 朱大培, 陈其明. 滑动领域克里金插值法的改进[J]. 计算机辅助设计与图形学学报, 2001, 13(8): 752-756. [本文引用:1]
[12] 璞定国, 王华, 田蔚文. 带非精确线搜索的调整搜索方向DFP算法[J]. 运筹学学报, 2004, 8(3): 1-9. [本文引用:2]
[13] 孙红泉. 地质统计学及其应用[M]. 徐州: 中国矿业大学出版社, 1990. 10. [本文引用:1]
[14] 侯景儒, 黄竞先. 地质统计学的理论与方法[M]. 北京: 地质出版社, 1990. 3 [本文引用:1]
[15] 刘国峰, 孟小红, 岳延波, 等. 克里金法在GPS数据内插中的应用[J]. 物探与化探, 2006, 30(2): 175-178. [本文引用:1]
[16] 孙仁铎. 空间变异理论及其应用[M]. 北京: 科学出版社, 2005 [本文引用:1]
[17] 孙红泉, 康永尚, 杜惠芝. 实用地质统计学程序集[M]. 北京: 地质出版社, 1997. [本文引用:1]
[18] 杨竹溪. 克里金法与区域化探制图[J]. 物探与化探, 1981, 5(6): 333-340. [本文引用:1]
[19] 杨学善, 秦德先, 邓明国. 地学空间数据库建设快捷方法研究[J]. 煤田地质与勘探, 2005, 33(5): 19-22. [本文引用:1]