引用本文
唐小平, 刘宽厚, 耿涛, 冯治汉. 曲网格克里金网格化方法及其在重力测量近区地形改正中的应用[J]. 物探与化探, 2015,39(4): 848-854.
TANG Xiao-Ping, LIU Kuan-Hou, GENG Tao, FENG Zhi-Han. Curved-grid kriging gridding method and its application to near-station terrain correction in gravity measurement[J]. Geophysical and Geochemical Exploration, 2015,39(4): 848-854.  
Doi:10.11720/wtyht.2015.4.31
Permissions
Copyright©2015, 物探与化探编辑部
? 《物探与化探》编辑部
曲网格克里金网格化方法及其在重力测量近区地形改正中的应用
唐小平1,2, 刘宽厚1, 耿涛1, 冯治汉1
1.中国地质调查局 西安地质调查中心,陕西 西安 710054
2.国土资源部 岩浆作用与找矿重点实验室,陕西 西安 710074

作者简介: 唐小平(1982-),男,硕士,助理研究员,主要从事矿产综合地球物理研究工作。E-mail:xiaopingtang@126.com

收稿日期: 2014-06-25
基金: 国家青年基金项目(41404110); 中国地质调查局项目(1212011220600、12120113031600); 陕西省面上基金项目(2015JM4133)
摘要

文中将研究一种高精度、强稳定性与灵活性的近区地改值计算方法。首先将克里金网格化技术与曲网格方法相结合,研究曲网格克里金网格化方法(简写为CGKG-M)及其扩边技术,进而实现数据的圆域网格化;再将该方法应用于圆域近区地改值的计算中,实现任意方位、任意环数的圆域近区地改值计算;最后进行了模型与实际地形的测试和误差分析。研究结果表明,CGKG-M近区地改算法具有方法简单、计算精度高、灵活性与稳定性强、计算速度快等特点,是与GTCS-1型近区地改仪数据采集格式相匹配的一种高效、快捷的近区地改值计算方法。

关键词: 曲网格克里金网格化法; 圆域; 近区地形改正
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)04-0848-07
Curved-grid kriging gridding method and its application to near-station terrain correction in gravity measurement
TANG Xiao-Ping1,2, LIU Kuan-Hou1, GENG Tao1, FENG Zhi-Han1
1.Xi'an Center of Geology Survey,China Geology Survey,Xi'an 710054,China
2.Key laboratory for the Study of Focused Magmatism and Giant ore Deposits,MLR,Xi'an 710074,China
Abstract

In this paper,a high-accuracy and strong stability near-zone terrain correction method is discussed.Firstly,combining Kriging gridding method with curved-grid computation technology,a Curved-Grid Kriging Gridding Method(short for CGKG-M)and its extending edge techniques are implemented to realize data-gridding in circle area;Next,this method is used to compute near-zone terrain correction value and realize the gravity measurement near-zone terrain correction value's computation which contains any angles and circles.Finally,some modeling tests,real data computation and error analysis of this method are carried out.The research result has shown that CGKG-M near-zone terrain correction value computation method has some characteristics,such as high computation accuracy,strong stability and flexibility.It is a simple,efficient and fast method for near-zone terrain correction value computation which matches the measurement data form of GTCS-1 gravity measurement near-station correction instrument.

Keyword: curved-grid kriging gridding method; circle region; near station terrain correction

近区地形改正是重力勘探的一项重要工作, 传统近区地改值的计算方法主要有基于扇区(圆域)与网格(方域)两种算法[1, 2], 但均有所不足。基于网格化的方域算法在计算时, 首先将矩形框区域网格化并求出总地改值, 再减去四个角部分地改值, 从而得出实际地改值。当地形特别复杂或地形数据较少时, 这种算法精度较低, 容易引起畸变。圆域(扇区)算法是将计算区域按方位和环数分成若干个扇区, 再求取每个扇区的平均地改值, 最后计算合成后的总地改值。该方法在求取扇区平均高差, 要求每个扇区参与计算平均高差的点数不少于5个, 计算时若扇区划分太小或数据量过小或分布不均匀时, 则难以满足上述要求; 若扇区太大, 测点周围的地形描述精度将会整体下降, 从而影响地改精度。总的来讲, 方域算法在消去远端四角地形影响时存有一定误差, 圆域算法则在方法灵活性与地形数据分布等方面受到限制。故而急需研究一种高精度、强稳定性与灵活性的近区地改值计算方法, 以克服传统近区地改中存在的诸多问题。

近区地改算法最早是圆域地改算法, 由Hammer于1939年提出[3], 并沿用至今。随着计算机技术的发展, 上世纪60年代开始出现基于计算机软件开发的方域网格化算法[4], 并在此后的发展中, 该方法在重力近区、中区地改中得到了很大的发展和应用[5, 6]。一直以来, 地形数据精度及计算方法对重力地形改正的影响受到了广泛关注, 冯治汉[7]使用了直立长方体法, 并采用不同网格间距的高程数据计算北祁连地区的重力调查地形改正值, 并系统地讨论了地改精度, 得出越小网格距的高程数据对地形的模拟程度越高; 张俊等[8]为了得出高程数据网格间距对表面积分法、直立长方体法和平均高程直立长方体积法计算中区地形改正值精度的影响, 对选择的450测点, 采用不同网格间距的高程数据, 以中区分段的方式比较了三种方法的地改精度, 得出表面积分法受高程数据网格化间隔的影响较小, 直方体受到的影响最大, 同时指出影响中区地改精度的最大影响地段为50~500 m。, 随着现在光学与测量技术的发展, 在近区地改方面, 为了解决地形测量的精度问题, 近年来人们开始研制基于现代光学测量仪器的近区地形改正仪器系统。Schiavone D等对摄影制图、数字化地图和高精度的激光扫描数据进行了比较, 得出了激光扫描数据精度最高、地形重建时间最短的结论[9], 不久又研制出了基于激光扫描技术的近区地改仪[10], 但该仪器价格昂贵, 比较笨重; 刘宽厚、耿涛等研究和实验了基于激光测距技术下的近区地改, 研制出了重力测量近区地形改正系统[11], 该系统具有使用简单、仪器轻便、能适应复杂地形等特点, 主要针对0~20 m内的近区地改。本算法即为该系统的配套算法之一。

曲网格技术是基于复杂地形与内部结构建模的一类数值建模方法。1985年, Thompson等[12] 系统地阐述了曲网格技术在各类方程、各种模型中使用的基本理论; 随后, 这一技术被广泛的应用于地球物理的各个领域[13, 14], 并在此基础上发展出了正交网格等更有效的计算网格[15, 16]。

地球物理中的网格化技术很多, 如线性插值法、多元二次函数、反插值法以及克里金网格化法等[17]。克里金网格化法最早由南非采矿工程师Krige D G提出, 故命名为“ 克里金” 法[17], 后经Matheron[18, 19]发展而逐步完善, 是一种空间内插法。

文中通过引入曲网格数据计算转化原理, 先将圆域测量数据按方位与距离展开成方域, 再在方域中应用克里金网格化法进行网格化计算, 最后应用曲网格数据计算反转化原理还原到圆域中, 计算出相应点高差, 并采用圆域地改值计算方法计算出相应的地改值。

1 方法原理
1.1 圆的曲网格计算与极坐标系下克里金法

在坐标转换中, 极坐标系(θ , r, h)与直角坐标系(x, y, z)之间的转换关系为

x=rcosθ, y=rsinθ, z=h。(1)

对式(1)引入曲网格计算, 将极坐标转换为计算坐标(ε , η , z)。设计算区域为:ε ∈ (0, 1), η ∈ (0, 1), 得

ε=θ2π, η=r-r1r2-r1, z=h。(2)

将上式进行变形, 从而得到(θ , r, h)的反算公式

θ(ε)=2πε, r(η)=r1+(r2-r1)η, h=z。(3)

将式(3)代入式(1)简化得到的泛函关系

x(ε, η)=r(η)cos(ε), y(ε, η)=r(η)sin(ε), h=z。(4)

将式(4)代入克里金网格化方法中, 求取曲网格克里金网格化的基本计算公式。常规克里金方法

Z* =m(u)+∑a=1n(u)[λa(u)-m(u)], (5)

则在曲网格下的计算公式即表示为

Z* =m(u)+∑a=1n(u)[λa(u)-m(u)]=m[u(x, y, z)]+∑a=1n(u){λa[u(x, y, z)]-m[u(x, y, z)]}=m{u[x(ε, η), y(ε, η), z]}+∑a=1n(u){λa[u(x(ε, η), y(ε, η), z)]-m{u[x(ε, η), y(ε, η), z)]}。(6)

式(6)即为最终曲网格克里金网格化法, 该式实际控制坐标为(ε , η , z), 通过式(6)可以计算出任意给定的(ε , η )点上的坐标高差值z, 而通过式(3)可以求出(ε , η , z)所对应的极坐标(θ , r, h), 从而实现了曲网格克里金网格化方法在圆域网格化中的应用。

1.2 曲网格网格化方法在近区地改中的应用

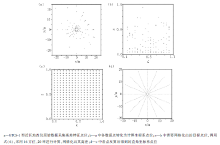
首先说明GTCS-1型仪器的数据格式, 数据以重力测点为圆心, 按方位和环数分布于测点四周(图1a), (0, 0)为测点坐标, 数据测量点数位于其周围, 稀疏分布在半径20 m的圆形内。将GTCS-1的测量数据转换为(θ , r, h)后, 应用式(2), 计算坐标系中的(ε , η , z)

ε=θ2π, η=r-r1r2-r1, z=h。(7)

其中:θ 表示方位角度; r为平距; h为高差; r1、r2表示地改外半径和内半径; 在0~20 m近区地改中, r2=20 m, r1=0.5 m, 0≤ θ ≤ 2π , 0≤ ε ≤ 1, 0≤ η ≤ 1。经过式(2)可将(θ , r, h)转化为曲网格的计算域(ε , η , z), 代入式(6)中, 即可实现任意(ε , η )下的z值求取, 进而调用反算公式(3), 即可得到相应的(θ , r, h)。具体应用过程如图1b~图1d所示, 图1b为将GTCS-1的测量数据转换为(θ , r, h)后, 按式(7)展布于计算空间之中, 将图2b代入式(6)中, 对各节点的高差进行网格化(图1c), 最后通过式(4)即可回到物理空间, 成标准的圆环分布(图1d)。假如这些点刚好为该扇区的重心位置, 则可计算出所在扇区的地改值, 将所有扇区地改值叠加, 即可得出最终地改值。

另外, 从图1c中可以看出, 与普通网格化方法相似, 可以自由选择η (对应环数)和ε (对应方位数)的间隔, 而在图1d也会得到相应的空间坐标, 从而可实现任意方位、任意环数的近区地改值计算, 至于地形测量精度与网格参数选取之间的关系, 则不在本文研究范围之内。

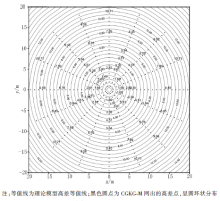
图1 曲网格克里金网格化方法(CGKG-M)在近区地改(0~20 m)中的应用示意

1.3 周期与对称扩边技术

扩边技术是网格化中重要的一项工作, 常用的扩边技术有常数扩边、余弦扩边等。文中根据测量数据具有周期性和关于圆心对称的特征, 采用周期扩边与对称扩边技术相结合, 实现了对原始数据的实数据扩边, 从而大大提高了网格化精度。图2为对称扩边与周期扩边技术示意图, A区为实测数据区, 模拟GTCS-1型近区地改仪野外数据采集点位分布, 按16方位、单方位20点测量, 每个方位控制22.5° , 测量距离大于20 m, 转换到计算域中(A区所示), 由C可知, GTCS-1型近区地改仪的采集数据是以测点为圆心的圆内, 而圆具有周期性和圆点对称性的特点, 从而可以使用原始测量的数据对网格化区域进行扩边。如图B所示, 根据周期性特征, 第1方位的左边可使用第16、15、…等方位进行扩边, 而第16方位的右边可使用第1、2、…等方位进行扩边; 图2c给出圆心对称扩边结果, 如第1方位与第9方位关于圆心对称, 所以第1和9方位可互为中心对称扩边数据, 以此类推, 可实现各方位关于圆点对称的数据扩边。

图2 周期与对称扩边技术示意

完成上述扩边后, 对A区上部的扩边可自由选择常数据补0或余弦扩边等扩边方法, 这里不多做阐述。

2 模型测试
2.1 测试模型一:圆锥体模型

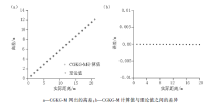
选用圆锥体模型对本方法进行测试, 锥体斜面倾角30° , 水平半径30 m, 采用16方位、10环对理论数据抽稀, 以模拟该地形下的GTCS-1型近区地改仪数据采集情况。再应用曲网格克里金网格化方法(CGKG-M)对抽稀数据进行地形重构, 并与理论模型进行比较, 结果如图3、图4所示。图3给出了理论模型与CGKG-M重构地形的高差比较, 从图中可以看出CGKG-M重构地形与理论模型差距很小, 几乎完全吻合。为了进一步说明二者之间的差异, 图4给出了CGKG-M重构地形与理论模型之间的剖面比较, 图4a为二者的高差, 圆点代表理论模型, “ +” 字地表CGKG-M重构地形, 二者几乎完全重合, 将该剖面的理论地形高与CGKG-M重构地形高相减, 从而得出二者的实际差距δ h=H-h, 图4b给出了δ h的分布情况, 从图4b中可以看出δ h很小, 在0值附近成直线分布, 均方根误差为0.000 046 m, 说明了本方法精度较高。

图3 凹陷模型等高线及其曲网格克里金网格化技术重构

图4 曲网格克里金网格化法高差点重构与理论值之间的比较

2.2 测点数据测试

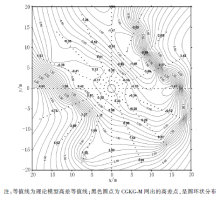
随机选择野外实测模型进行数据处理分析, 以测试本方法的实际应用情况。选择一处中间为沟, 三面为台地的模型作为本次试验的理论模型, 采用16方位、5~8点测量模式, 先将测得数据应用Surfer进行高差网格化处理, 选用参数如下:克里金法为网格化方法, x、y坐标均为-20~20 m, 网格间距1 m。将网格化成果画出等值线, 间隔0.25 m, 再采用本文所述CGKG-M方法进行网格化计算, 结果如图5中黑色圆点所示。从图中可以看出, 黑色圆点所注明的高差与等高线大多能对应, 只有较远的地方和个别地方有所差异, 这是由于:网格化方位与测量方位不完全重合, 以及远区数据量较少的缘故, 但总体上讲这两种方法地形重构效果相当, 说明了本方法精度可与常用的Surfer网格化方法媲美。

图5 复杂模型等高线及其曲网格克里金网格化技术重构

3 误差分析

前面2.1、2.2节给出了两种不同模型的数据测试结果, 进行了关于高差的相关误差分析, 所以这里不再作有关高差的误差分析了, 主要进行地改值的误差分析。选用圆锥体模型, 选择锥体倾角变化范围为0° ~75° , 水平半径为20 m, 分别采用锥体理论地改值计算与基于CGKG-M方法的圆域地改值计算[1, 2]:

锥体理论公式

Δg=2πGρRn(1-cosi)

扇形公式

ΔgT=2πGρRn(Rm+1-Rm+Rm2+Δh2-Rm+12+Δh2)

单位均为10-8m/s2, 计算结果如图6所示。

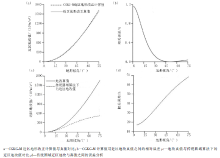
从图6a中可以看出CGKG-M计算值与理论值地改值几乎重合, 只有当锥体倾角变得很大时稍稍产生差异, 而这个差异与理论地改值之间的相对误差, 如图6b所示, 随着锥体倾角的增加, 下降趋势明显, 当倾角大于50° 又有所上升, 最终收于0.2%左右。这说明了本文所采用的基于CGKG-M的近区地改值计算方法精度较高, 稳定性较强, 另外, GTCS-1型近区地改仪最大测量仰角为70° 左右, 所以本方法完全适应该仪器的数据处理范围, 无需担心发散现象。

图6c、6d为文献[1, 2]所示传统平面克里金网格方法计算的地改值及其与理论值之间的相对误差分析, 从图中可以看出传统平面克里金网格方法随着坡度增大, 地改值与相对误差均逐渐增大, 这是由于随着地形角度增加, 平面网格的四角对地改值的影响逐渐增大, 该方法稳定性较差。

图6 曲网格克里金网格化法(CKG-M)与传统方法近区地改计算值及其与理论地改值之间的误差分析

4 结论

文中首先详细介绍了曲网格克里金网格化方法(CGKG-M)的原理与推导过程和GTCS-1近区地改仪的数据特点, 再系统介绍了该方法的周期扩边与对称扩边, 进行有关模型的地形重构测试和高差精度对比及其与surfer进行实际数据的网格化地形重构比较, 最后详细介绍了基于本方法的圆域近区地改值计算, 并进行了误差分析, 总结出该方法具有精度高、稳定性强、使用方便、可与GTCS-1型近区地改仪配合使用等特点, 具有广泛的应用前景。除了在近区地改中被应用外, 该方法还可在中、远区地改及其他相关圆域网格化计算中使用。同时, 对开发变网格圆域网格化方法具有重要意义。

The authors have declared that no competing interests exist.

参考文献
[1] DZ0004-91重力调查技术规范(1∶50000)[S]. 1991, 中华人民共和国国土资源部. [本文引用:3]
[2] DZ/T0171-1997大比列尺重力勘察规范[S]. 1997, 中华人民共和国国土资源部. [本文引用:3]
[3] Hammer S. Terain corrections for gravimeter stations[J]. Geophysics, 1939, 4: 184-194. [本文引用:1]
[4] Nagy D. The gravitational attraction of a right rectangular prism[J]. Geophysics, 1966, 31: 362-371. [本文引用:1]
[5] Forberg R. Gravity field terrain effect computations by FFT[J]. Bull Geod, 1985, 59: 342-360. [本文引用:1]
[6] Li Y C, Sideris M. Improved gravimetric terrain correction[J]. Geophysical Journal of International, 1994, 119: 740-752. [本文引用:1]
[7] 冯治汉. 区域重力调查中的中区地形改正方法及精度[J]. 物探与化探, 2007, 31(5): 455-458. [本文引用:1]
[8] 张俊, 张宝松, 邸兵叶, 等. 高程数据网格间距对重力中区地形改正精度的影响[J]. 物探与化探, 2014, 38(1): 157-161. [本文引用:1]
[9] Schiavone D, Capolongo D, Loddo M. High resolution dems for near station terrain correction in gravimetery[R]. EGM2007 International workshop, 2007. [本文引用:1]
[10] Schiavone D, Capolongo D, Loddo M. Near-station topographic mases correction for high-accuracy gravimetric[J]. Geophysics Prodpecting, 2009, 57(5): 739-751. [本文引用:1]
[11] 刘宽厚, 耿涛, 杨怀英, 等. 基于便携激光测距仪的重力测量近区地形改正系统[J]. 物探与化探, 2012, 36(3): 403-408. [本文引用:1]
[12] Thompson J F, Warsi Z U A, Mastin C W. Numerical Grid Generation: Foundations and Applications[P]. North Holland , ISBN: 044400985X, 1985. [本文引用:1]
[13] Fomberg B. The pseudo spectral method: accurate representation of interfaces in elastic wave calculations[J]. Geophysics, 1988, 53: 625-637. [本文引用:1]
[14] Nielsen P, Flemming I, Berg P, et al. Using the pseudo-spectral method on curved grids for 2D elastic forward modeling[J]. Geophysical Prospecting, 1995, 43: 369-395. [本文引用:1]
[15] 蒋丽丽, 孙建国. 基于Poisson方程的曲网格生成技术[J]. 世界地质, 2008, 27(3): 298-305. [本文引用:1]
[16] 孙建国, 蒋丽丽. 用于起伏地表条件下的地球物理场数值模拟的正交曲网格生成技术[J]. 石油地球物理勘探, 2009, 44(4): 494-500. [本文引用:1]
[17] 郭良辉, 孟小红, 郭志宏, 等. 地球物理不规则分布数据的空间网格化法[J]. 物探与化探, 2005, 29(5): 438-442. [本文引用:2]
[18] Matheron G. Principles of geostatistics[J]. Economic Geology, 1963, 58: 1246-1266. [本文引用:1]
[19] Matheron G. The intrinsic rand om functions, and their applications[J]. Adv. Appl. Prob. , 1973, 5: 439-468. [本文引用:1]