引用本文
赵亚博, 刘天佑. 迭代Tikhonov正则化位场向下延拓方法及其在尕林格铁矿的应用[J]. 物探与化探, 2015,39(4): 743-748.
ZHAO Ya-Bo, LIU Tian-You. The iterative Tikhonov regularization method for downward continuation of potential fields and its application to the Galinge iron deposit[J]. Geophysical and Geochemical Exploration, 2015,39(4): 743-748.  
Doi:10.11720/wtyht.2015.4.14
Permissions
Copyright©2015, 物探与化探编辑部
? 《物探与化探》编辑部
迭代Tikhonov正则化位场向下延拓方法及其在尕林格铁矿的应用
赵亚博, 刘天佑
中国地质大学(武汉) 地球物理与空间信息学院,湖北 武汉 430074
通讯作者:刘天佑(1945-),男,中国地质大学(武汉)地球物理与空间信息学院。E-mail:liuty@cug.edu.cn

作者简介: 赵亚博(1990-),男,中国地质大学(武汉)地球物理与空间信息学院在读硕士研究生,研究方向为地球物理数据处理与解释。E-mail:zyabo@foxmail.com

摘要

解析延拓是一种广泛应用的位场处理方法,向下延拓可以压制深部地质体的影响,突出浅部异常。但是,向下延拓滤波因子是一个高通滤波器,会造成下延结果震荡,从而限制了该方法在实际资料中的应用。文中详细介绍并实现了迭代Tikhonov正则化向下延拓方法,在理论模型上将该方法与传统频率域延拓方法进行对比,表明迭代Tikhonov正则化向下延拓方法的有效性;并将该方法应用于青海尕林格铁矿区磁测资料的处理解释中,下延结果与钻探情况相符,说明在厚覆盖层的勘查区中,运用迭代Tikhonov正则化向下延拓方法能够有效地提高资料处理解释的效果。

关键词: 重磁勘探; 向下延拓; 迭代Tikhonov正则化; 尕林格铁矿
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)04-0743-06
The iterative Tikhonov regularization method for downward continuation of potential fields and its application to the Galinge iron deposit
ZHAO Ya-Bo, LIU Tian-You
School of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
Abstract

Analytic continuation for potential field is a widely used method for processing and interpretation, because downward continuation can suppress the influence of deep geological bodies and protrude the shallow layer anomaly. However, the downward continuation filter factor is a high-pass filter, leading to unstableness of the result, and therefore it can not be used to process the real data. The authors systematically studied and implemented the iterative Tikhonov regularization method for downward continuation of potential fields. In contrast to the continuation of potential field on the theoretical model, the iterative Tikhonov regularization method indicates better effectiveness than frequency domain. The authors also applied this method to Galingeiron deposit's magnetic data processing, and the results indicate that the iteration Tikhonov regularization method for downward continuation of potential fields is worthy to use in heavy overburden exploration areas.

Keyword: gravity and magnetic exploration; downward continuation; iterative Tikhonov regularization; Galingeiron deposit

上世纪70年代初, 我国开始将计算机应用于地球物理勘探资料的处理解释。其中, 位场解析延拓方法是一种应用极广泛的方法, 该方法利用数学原理, 将观测平面换算到高于它的平面(向上延拓), 可以压制浅部干扰、突出深部异常; 而将观测平面换算到低于它的平面(向下延拓), 可以压制深部地质体的影响、突出浅部异常。多年来, 向上延拓换算得到了广泛的应用, 但是向下延拓却很少使用, 究其原因是通常采用的向下延拓方法是利用傅立叶变换实现的, 也称频率域延拓方法[1], 其滤波因子eω h(h> 0)是一个高通滤波器, 它对观测数据中的噪声有明显的放大作用, 会造成下延结果严重震荡, 在处理实际资料时几乎无法利用。

频率域直接向下延拓结果中, 针对由高频噪声引起的严重震荡问题, 在实际应用中通常采用低通滤波的方法压制高频噪声, 减小高频噪声对下延结果的影响, 但是最多只能下延3~5倍点距, 下延深度更大时会出现震荡和信号失真。出现这种问题有两方面原因:首先, 由于位场的观测信号中有用信息和噪声的频谱是叠加的, 低通滤波器不可能将全部高频噪声滤去, 随着下延深度增大, 高频噪声的影响会迅速增加, 直至淹没有用信息; 其次, 虽然通过低通滤波可以压制高频噪声, 但是也会造成有用信号的丢失, 在此基础上进行下延运算, 会造成结果的偏差。

通过向下延拓可以使得“ 观测面” 更接近场源, 得到实际观测面以下空间的异常场分布特征, 增加重磁位场资料的分辨率。基于向下延拓对重磁异常定性解释的重要性, 近年, 向下延拓方法又重新唤起人们的重视, 徐世浙院士最早提出位场延拓的积分— 迭代法[2], 这种方法可以在无噪声环境中向下延拓20倍点距而不产生震荡。之后, 国内学者对这类迭代正则化方法又作了大量深入的探讨[3, 4, 5]。但是探讨大多停留在理论上, 鲜有将这些方法用于实际资料处理中。

文中介绍了迭代Tikhonov正则化向下延拓方法, 并与传统频率域延拓方法及附加低通滤波过后的频率域延拓方法进行对比, 随后将该方法应用于实际磁测资料的处理中, 得到了较好的地质效果。

1 迭代Tikhonov正则化方法
1.1 方法原理

向下延拓问题的观测方程为

d=Gx+δd, (1)

其中:d为观测的位场值, G为向上延拓矩阵, x为延拓面位场值, δ d为观测误差。上式的最小二乘解为

x=(G* PG)-1G* Pd, (2)

其中:P为权矩阵, G* 为G的伴随矩阵。观测的位场值d中包含观测误差δ d, 较小的观测误差δ d会产生很大的计算误差δ x, 导致计算的延拓面位场值x不稳定。针对这一不适定问题, Tikhonov[6]采用不迭代的正则化方法进行解决。其正则化解为

xα=(G* PG+αI)-1G* Pd, (3)

其中:I为单位矩阵, α > 0是Tikhonov正则化参数, 该方法通过Tikhonov正则化参数α 对解的精度和稳定性进行平衡。

20世纪70~80年代曾对不迭代Tikhonov正则化方法有过研究[7, 8], 但未得到广泛应用, 因为不迭代Tikhonov正则化方法存在饱和效应[9], 即不能在提高解的光滑性的同时提高解的精度。对此, T Schroter等[10]对不迭代Tikhonov正则化方法进行了推广, 提出了迭代Tikhonov正则化方法[11]

x0=0(G* PG+αI)xn=αxn-1+G* Pd, (4)

当迭代次数n=1时, 为不迭代Tikhonov正则化方法。对式(4)运用数学归纳法

xn=I-(αIG* PG+αI)nG-1Pd, (5)

其中: I-(αIG* PG+αI)nG-1P为迭代Tikhonov正则化方法的正则化算子, Tikhonov正则化参数α 和迭代次数n是该方法的两个正则化参数。

1.2 滤波因子

迭代Tikhonov正则化方法也可以在波数域中进行, 其滤波因子为

H={1-[1-Ψ(α)Φ]n}Φ-1, (6)

其中:Φ -1=eω h为下延算子, Φ =e-ω h为上延算子, Ψ (α )= e-ωhe-2ωh+α为不迭代Tikhonov正则化方法的滤波因子, α 为Tikhonov正则化参数, n为迭代次数。其滤波特性如图1所示, 迭代Tikhonov正则化方法可以通过Tikhonov正则化参数α 及迭代次数n这两个参数调节滤波器的通带范围, 增加迭代次数n或者减小Tikhonov正则化参数α 可以使得滤波器的带通特性更加明显, 而我们通常使用的频率域向下延拓滤波因子是高通滤波器。

图1 频率域直接向下延拓和Tikhonov迭代正则化向下延拓的滤波特性曲线

2 理论模型试验及正则化参数的选取

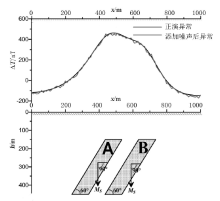
本文设计了A、B两个平行排列的倾斜二度板状体模型, 两板水平间隔为100 m, 具体参数设置见表1, 采样点距10 m, 采样点数101个。为了模拟实际观测值, 首先在模型正演值的基础上添加均值为零、标准差为10 nT的高斯白噪声, 模型正演结果及添加噪声后异常曲线(图2)可见异常形态简单平稳, 近乎单峰, 直接根据模拟异常无法定性分辨出场源体的个数、位置等信息, 这种情况下可以使用迭代Tikhonov正则化方法进行试验, 检验这种方法的效果。下延计算的精度采用下延结果与对应深度的正演理论值之间的均方误差进行衡量。

表1 理论模型参数

图2 模型正演结果及添加噪声后的异常曲线

2.1 不同方法的下延结果

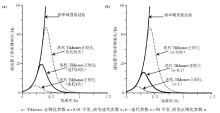
文中分别采用频率域直接下延、低通滤波后频率域直接下延和迭代Tikhonov正则化方法对加噪声的模拟异常进行下延处理。直接采用频率域延拓方法下延10 m(即1倍点距)时, 下延结果由于原始异常中的高频噪声影响, 出现明显震荡(图3a), 无法判断场源个数。运用匹配滤波方法将高频噪声压制后, 再采用频率域直接延拓方法进行下延处理, 当下延至40 m时也出现了明显的高频振荡(图3b), 这样的结果显然是不能用于解释的。最后, 采用迭代Tikhonov正则化方法对模拟观测值进行下延, 下延深度由10~140 m(近场源顶), 所得到的异常曲线形态光滑(图3c和3d), 与对应深度的正演理论值对比精度较高(图3c), 可以明显分辨出A、B两个场源体的位置(图3d)。

图3 不同下延方法的计算结果

2.2 正则化参数的选取

选取正则化参数的方法可以分为先验选取和后验选取两类方法。对于位场下延问题, 观测的误差精度等先验信息是不可能精确得到, 因此先验方法很少用到, 一般使用后验方法, 最常见的有广义交叉验证方法 (Generalized Cross— validation, GCV)[12]、L曲线法[13]和岭迹法[14]等。

迭代Tikhonov正则化方法有Tikhonov正则化参数α 和迭代次数n两个正则化参数, 这两个正则化参数均可以起到调节迭代Tikhonov正则化方法对应滤波器滤波特性的作用, 为了简单起见, 文中选用了固定的Tikhonov正则化参数α , 通过改变迭代次数n, 分析其对下延结果的影响。

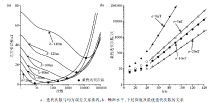
图4a为采用迭代Tikhonov正则化方法对模拟观测值下延不同深度时迭代次数与均方误差的关系曲线。模型试验结果表明, 该方法在下延深度较大时仍有较高的精度, 随着迭代次数的增加, 均方误差先减小后增大, 下延深度越大, 对应每个深度最小均方误差的最优迭代次数越大。文中又对模型正演值分别添加了均值为零、标准差σ 为0、5、10和20 nT的高斯白噪声模拟观测值, 并求取了各种噪声水平下下延深度不同时的最优迭代次数(图4b), 可见下延深度不大(10~40 m)时, 深度增大时最优迭代次数相对增加缓慢, 而当下延深度从50 m(即5倍点距)开始, 随着下延深度的增大, 最优迭代次数呈指数增加。

图4 迭代Tikhonov正则化方法的最优迭代次数选择

3 青海尕林格铁矿的应用实例

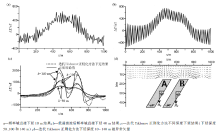
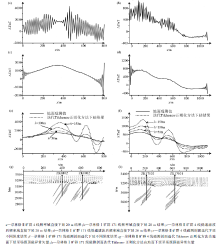
尕林格铁矿区位于塔柴板块南缘祁漫塔格成矿带[15], 矿床类型多为喷流沉积改造型, 少数为矽卡岩型。矿区广泛内分布第四纪陆相砂砾沉积, 砂砾层厚117~210 m。由于砂砾层覆盖较厚, 导致矿致磁测异常形态光滑, 所含信息较少, 为了提高磁测资料的分辨率, 选取了Ⅱ 矿群4线和Ⅰ 矿群171线磁测剖面进行了下延处理, 磁测剖面点距为10 m, 两条剖面的磁测观测值和地质剖面见矿情况见图5, 可见磁测受巨厚的沉积层影响, 异常较为低缓。

图5 尕林格铁矿群水平叠加矿体剖面

图6 尕林格铁矿群磁测剖面下延结果

采用频率域向下延拓、低通滤波后频率域向下延拓和迭代Tikhonov正则化方法对两条剖面下延的结果见图6。采用频率域向下延拓下延至20 m时, 观测异常值中的高频噪声被放大, 结果震荡较为剧烈(图6a、6b)。匹配滤波压制高频噪声后进行频率域直接延拓的结果见图6c和6d, 由于已经压制了高频噪声, 异常的主体部分相对光滑, 但由于扩边等问题引发的边界效应明显, 在异常的边界处震荡明显, 随延拓深度增加, 会使得边界效应扩散, 淹没有用信息。

采用迭代Tikhonov正则化方法对两条磁测剖面进行下延处理, 下延计算中的正则化参数通过GCV法进行选取。下延50、100和150 m的结果见图6e、6f, 原始观测结果中水平叠加的层状矿体由于埋深大, 没有明显的双峰异常, 经过向下延拓50、100和150 m后, 下延结果稳定, 水平叠加异常的特征十分显著。通过迭代Tikhonov正则化方法由地面下延至场源顶得到的磁异常矢量图见图6g和6h, 揭示了异常场在地下空间的分布, 两条剖面的结果均可以明显的分辨出场源体的位置, 提高了对矿区磁异常场分布特征的认知。

4 结论

文中详细介绍了迭代Tikhonov正则化方法的方法, 并通过建立理论模型对该方法进行了试验, 并与频率域向下延拓及低通滤波后频率域向下延拓方法进行了对比, 得出迭代Tikhonov正则化向下延拓方法延拓深度大且结果稳定。将迭代Tikhonov正则化方法用于青海尕林格铁矿磁测资料处理, 结果表明迭代Tikhonov正则化方法的下延结果稳定, 能够有效识别水平叠加矿体异常, 在厚覆盖层的勘查区中, 迭代Tikhonov正则化向下延拓方法是一种值得推广采用的处理解释方法。

The authors have declared that no competing interests exist.

参考文献
[1] 侯重初. 位场的频率域向下延拓方法[J]. 物探与化探, 1982, 6(1): 33-40. [本文引用:1]
[2] 徐世浙. 位场延拓的积分—迭代法[J]. 地球物理学报, 2006, 49(4): 1176-1182. [本文引用:1]
[3] 曾小牛, 李夕海, 刘代志, 等. 积分迭代法的正则性分析及其最优步长的选择[J]. 地球物理学报, 2011, 54(11): 2943-2950. [本文引用:1]
[4] 曾小牛, 刘代志, 李夕海, 等. 位场向下延拓的改进迭代维纳滤波法[J]. 地球物理学报, 2014, 57(6): 1958-1967. [本文引用:1]
[5] 姚长利, 李宏伟, 郑元满, 等. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报, 2012, 55(6): 2062-2078. [本文引用:1]
[6] Tikhonov A N, Arsenin V Y. Solutions of Ⅲ-Posed Problems[M]. New York: JohnWiley and Sons, 1977. [本文引用:1]
[7] 《重磁资料数据处理问题》编写组. 重磁资料数据处理问题[M]. 北京: 地质出版社, 1977. [本文引用:1]
[8] 梁锦文. 位场向下延拓的正则化方法[J]. 地球物理学报, 1989, 32(5): 600-608. [本文引用:1]
[9] Kirsch A. An introduction to the mathematical theory of inverse problem[M]. New York: Springer, 1996. [本文引用:1]
[10] Schroter T, Tautenhahn U. On the optimality of regularization methods for solving linear ill-posedproblems[J]. Journal for Analysis and its Applications, 1994, 13(4): 697-710 [本文引用:1]
[11] 傅初黎, 李洪芳, 熊向团. 不适定问题的迭代Tikhonov正则化方法[J]. 计算数学, 2006, 28(3): 237-246. [本文引用:1]
[12] Jansen M, Malfait M, Bultheel A. Generalized cross validation for wavelet thresholding[J]. Signal Processing, 1997, 56(1): 33-44. [本文引用:1]
[13] Hansen P C. Analysis of discrete ill posed problems by means of the L-curve[J]. SIAM Review, 1992, 34(4): 561-580. [本文引用:1]
[14] 王振杰. 大地测量中不适定问题的正则化解法研究[D]. 北京: 中国科学院研究生院(测量与地球物理研究所), 2003. [本文引用:1]
[15] 张德全, 丰成友, 李大新, 等. 柴北缘—东昆仑地区的造山型金矿床[J]. 矿床地质, 2001, 20(2): 137-146. [本文引用:1]