常用雷达解释软件将主机接收到的电磁波振幅v_s时间序列按测点顺次排列, 从而得到雷达图像, 在常规直线探测中, 面状构造的反射信息形成直线排列的同相轴, 球状体构造形成双曲线形同相轴, 因此分析雷达图像的同相轴特征即可对面状构造进行偏移校正, 也可反演计算球状体的空间几何参数。而圆形测线的法向反射路径和测线的半径相关, 平面

构造和球状地质构造在圆形测线的雷达图像中均表现为弧状同相轴, 凭借直观经验难以对反射信号作出定性、定量判断, 以下给出平面模型和球状体模型在圆形测线中的时距曲线方程。

代入介电常数将雷达图像纵坐标作时深转换后, 同相轴横坐标x为测线长度, 即圆形测线的圆弧长度, y为反射点的深度v_t/2。对于平面模型, 需要求解的参数有结构面的走向、倾角和结构面到测线的最小距离。

图1

	Figure Option ViewDownloadNew Window
	图1 平面模型三维视图

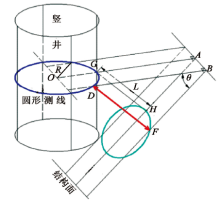
如图1所示, 当雷达天线为收发一体或收发距远小于探测深度时, 雷达射线DF垂直于结构面, 反射点轨迹为圆形测线在结构面上的投影, 为一椭圆。当圆形测线位于水平面上时, 圆形测线所在平面和结构面的夹角θ , 即为结构面的倾角, 其交线AB为结构面走向。整个圆形测线上G点到结构面的距离最小, 在雷达图像中可以很准确地读取同相轴顶点深度, 即为结构面到测线的最短距离GH, 同时读取G点的方位角α , 从而得到结构面的走向为α +90° 。当在平硐或斜井中探测时, 根据硐室的走向和倾角将θ 和α 作相应变换, 同样可得到结构面的走向和倾角。

根据图1中的空间几何关系, 可得到测线上任一测点的雷达同相轴反射信号D(x, y)关系式为

y=L+R[(1-sin(x/r)]sinθ, (1)

式中, L为平面到圆形测线的最短距离, 即实测曲线中顶点深度; R为圆形测线半径; θ 为反射平面与圆形测线平面的夹角。式(1)中已知R、L, 根据实测的(x, y)进行回归分析, 可得到θ 的最优解。

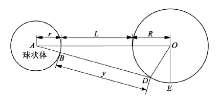
对于地下球状目标体, 在探地雷达的探测实践中, 由于雷达天线发射角有一定限制, 往往需要目标体与雷达测线足够近且目标体与雷达测线基本在同一平面内才能采集到较强的反射信号。如图2所示。考虑球心和圆形测线在同一平面内的情形, 测点D在球面的反射点为B, 反射路径BD反向延伸通过球心A, 则雷达图像同相轴D(x, y)的关系式为

y=R2+(L+R+r)2-2R(L+R+r)sin(x/R)-r, (2)

式中, L为实测曲线中顶点深度, R为圆形测线半径, r为球状体半径。式中已知R、L, 根据实测的(x, y)进行回归分析, 可得到r的最优解。

图2

	Figure Option ViewDownloadNew Window
	图2 球状体模型几何关系

设计4个模型:

Ⅰ :平面模型, L=3 m, R=4 m, θ =90°

Ⅱ :平面模型, L=3 m, R=4 m, θ =40°

Ⅲ :球状体模型, L=3 m, R=4 m, r=3 m

Ⅳ :球状体模型, L=3 m, R=4 m, r=3 m。

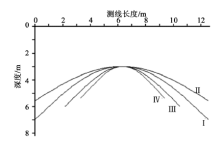
将式(1)和式(2)作正演计算, 得到结果如图3所示。

图3

	Figure Option ViewDownloadNew Window
	图3 探地雷达圆形测线平面和球体正演

分析图3中的曲线特征, 可定性归纳几点规律:

(1)曲线Ⅰ 是判断平面和球状体的分界线, 曲线曲率大于Ⅰ 者为球状体, 小于Ⅰ 者为平面。

(2)平面模型中曲线曲率越大, 则平面和圆形测线的夹角越大。

(3)球体模型中曲线曲率越大, 则球状体的半径越小。

(4)平面模型最大可探测范围为测线的半个圆周, 球状体模型最大可探测范围小于半个圆周, 且随球状体的半径减小而减小。

关于定量解释, 笔者提供实测曲线与正演计算结果相对比的曲线拟合方法, 基本原则是按照式(1)或式(2)过两点(含雷达同相轴顶点)绘制如图3中的正演曲线, 使所绘曲线与雷达图像同相轴吻合达到最佳, 再据此两点计算所需参数。

开发了相应解释软件, 其步骤为:

(1)雷达图像预处理。首先应对雷达图像进行x轴插值校正, 用以修正因雷达天线不均匀移动造成的x轴方向伸缩变形。校正的关键在于采集数据时必须在天线经过圆形测线的某些特征方位角时做上适当的标记, 可使用罗盘测定测线起点和其他特征方位角。因解释软件不对雷达数据直接成图, 需对雷达图像截图后再供解释软件使用, 因此应对雷达图像按纵横比例1∶ 1截取图像并保存为已知分辨率(像素/m)的图形文件。

(2)确定同相轴顶点。

(3)在雷达图像上点取同相轴顶点可以确定目标体与测线的最近距离, 此点的横坐标可用以计算结构面的走向, 并且可预先确定正演曲线的一点。

(4)追踪同相轴, 计算各项反演参数。

(5)在雷达图像上点取通过同相轴的另外一点, 即可计算式(1)或式(2)中的参数, 得出计算结果。

(6)修正曲线顶点和曲率以达到最佳拟合效果。

和数值拟合方法相比, 曲线对比方法不需要从雷达图像逐点读取数值, 且可以实时将实测曲线和正演曲线进行对比, 即时修正, 最大限度减少读数误差, 因而更加准确、快速, 且操作简单。

锦屏二级水电站高压管道竖井位于山体坡岸部位, 围岩为T₂y₅大理岩, 工区内褶皱挤压强烈, 岩层陡立, 断裂及岩溶发育强烈, 受构造控制因素影响甚至形成竖直向溶蚀管道。为了解竖井围岩的溶蚀状况, 施工过程中使用探地雷达即时进行了全程跟踪探测。竖井断面为圆形, 洞径8 m, 根据现场施工条件, 对洞周每掘进两个循环进行一次圆形测线探测。

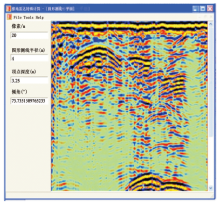
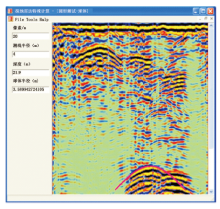
3号高压竖井高程1 386 m, 雷达探测成果如图4、图5所示。雷达图像中发现两处明显的弧状同相轴, 使用圆形测线解释软件判断为结构面和球状体。结构面距洞壁最近为3.25 m, 走向垂直最近点方位角, 倾角为74° , 根据两次连续探测结果判断倾向竖井方向, 将在探测位置下方被揭露。球状体距测线最近点21.9 m, 半径约3.6 m。经开挖证实, 结构面产状与探测结果基本吻合, 球状体实为相邻已开挖竖井, 设计半径为4 m, 两井壁相距22 m。可见解释成果基本准确, 且可根据不同位置的多次球状体反演结果进一步推测反射体是球状体或溶蚀管道, 并可计算其延伸方向。

图4

	Figure Option ViewDownloadNew Window
	图4 3号高压竖井雷达探测结构面解释成果

图5

	Figure Option ViewDownloadNew Window
	图5 3号高压竖井雷达探测球状体解释成果

目前, 国内隧道工程建设行业对于先进技术的应用逐渐呈现出全方位、多角度、立体化的发展趋势, 对隧道工程检测技术也提出了更高的要求。探地雷达作为一种常规物探手段在隧道工程质量检测中有不可替代的作用, 探地雷达有较高的分辨率, 精细化探测是大势所趋, 怎样提高探地雷达的探测水平、给出更加准确可靠的解释是每一个检测技术人员的责任。本文给出的圆形测线解释方法可应用于特殊条件的工程地质问题, 面对复杂的地质条件和施工环境, 应加深研究, 得出一些深入细致的解释方法, 更好地满足工程建设的需要。