引用本文
任泽, 刘修国, 张剑波, 高艳芳. 一种极值无偏的地球化学等值线图生成方法[J]. 物探与化探, 2015,39(3): 610-614.
REN Ze, LIU Xiu-Guo, ZHANG Jian-Bo, GAO Yan-Fang. A contour generating algorithm for solving excursion of geochemical concentration focus[J]. Geophysical and Geochemical Exploration, 2015,39(3): 610-614.
Doi:10.11720/wtyht.2015.3.30  
Permissions
Copyright©2015, 物探与化探编辑部
《物探与化探》编辑部
一种极值无偏的地球化学等值线图生成方法
任泽1, 刘修国1, 张剑波1, 高艳芳2
1.中国地质大学 信息工程学院,湖北 武汉 430074
2.中国地质科学院 地球物理地球化学勘查研究所,河北 廊坊 065000

作者简介: 任泽(1989-),男,硕士研究生,从事地理信息科学和地球化学相关的研究工作。E-mail:renzeGIS@126.com

收稿日期: 2014-12-25
基金: 中国地质调查局地质调查工作项目(12120113026700); 国家自然科学基金项目(41001225); 长江三角洲重点地区三维地质调查项目(1212011220250)
摘要

利用野外获得的离散点数据制作地球化学图,通常采用规则矩形网格化和不规则三角网格化两种方式,前者易出现元素浓集区中心与极值点偏移的现象,后者难以保证等值线圆滑美观,且成图边界不规则。针对上述问题,笔者提出了一种极值无偏的地球化学等值线图生成方法,合并极值点与规则矩形网格点,并剔除畸形网格点,在此基础上构建不规则三角网,而后追踪等值线,通过极值点和规则矩形网格点分别控制等值线图的精度和可视化效果。实验结果证明,采用该方法制作的等值线图,元素浓集中心与极值点位置完全吻合,曲线光滑美观,同时有效解决了扩边问题。

关键词: 浓集中心偏移; 极值点提取; 畸形网格点剔除; 地球化学图件
中图分类号:P632 文献标志码:A 文章编号:1000-8918(2015)03-0610-05
A contour generating algorithm for solving excursion of geochemical concentration focus
REN Ze1, LIU Xiu-Guo1, ZHANG Jian-Bo1, GAO Yan-Fang2
1. Faculty of Information Engineering, China University of Geosciences, Wuhan 430074, China
2. Institute of Geophysical and Geochemical Exploration, CAGS, Langfang 065000, China
Abstract

Grid and TIN are usually used during the computer graphics of medium-large scale geochemical contour maps; nevertheless, the former generates the problem of "excursion of geochemical concentration focus", while the latter can't ensure smooth contours as well as regular border. Aimed at solving these problems, this paper presents a contour generating algorithm for discrete data based on extreme points constraint. Firstly, the original sampling points and grid points are merged. Secondly, the abnormal grid points are rejected. Finally, triangulated irregular networks and track contour lines are built. The original sampling points and grid points are merged to improve accuracy and visualization of contour lines. The experimental results show that geochemical concentration focus coincides with extreme points in the contour map generated by this method, which is visually smooth and edge-expanded.

Keyword: excursion of geochemical concentration focus; extreme points extraction; rejection of abnormal grid points; geochemical map

在进行水系沉积物地球化学测量工作中, 一般采用沿沟谷水系的树枝状网代替正规测网, 采样所得数据为不均匀分布的离散点数据[1]。利用上述数据, 在计算机辅助下绘制多个元素的地球化学图和异常图, 是地球化学勘查工作中的重要内容之一。

传统的等值线绘制主要基于规则矩形格网(Grid)和不规则三角网(triangulated irregular networks, TIN)。Grid数据通常由离散点数据经过插值算法而得, 虽然可以避免因数据分布不规则所带来的影响, 但受插值策略和参数的影响, 容易造成采样点附近数据失真, 出现元素浓集中心与极值点位置不吻合的现象。另一方面, TIN数据是由直接对离散点数据实施三角化过程而来, 能够保证数据精度, 但其绘制的等值线不够圆滑, 影响可视化效果, 同时还需进行扩边处理, 以保证等值线图边界与工区边界一致。

为了兼顾制图精度与可视化效果, 笔者结合中大比例尺化探水系沉积物数据特征, 提出了一种极值无偏的地球化学等值图生成方法:从原始采样点中提取极值点, 与规则矩形网格节点合并, 然后通过筛选策略剔除合并后点集中的畸形网格点, 最后构建三角网并追踪等值线, 分别通过原始采样点和规则矩形网格点控制等值线图的精度和可视化效果。以冀东某地区的1∶ 50 000水系沉积物采样点为实验数据, 通过对比实验说明, 该方法有效解决了元素浓集中心与极值点偏移的问题, 同时能够保证地球化学图的图面效果。

在中国地质科学院地球物理地球化学勘查研究所与中国地质大学(武汉)联合开发的“ 中大比例尺化探数据一体化处理” 系统中, 已经采用了笔者提及的方法, 目前, 该系统软件正在全国化探领域进行试用推广。

1 问题描述

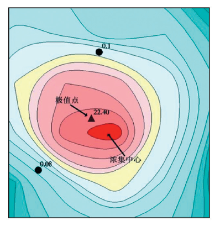
在编制地球化学图中, 规则矩形网格化法(Grid)是常用的离散数据网格化方法[2]。得益于矩形格网的规则性和均匀性, 利用Grid方法绘制的等值线图圆滑、自然、美观。然而, 该方法将网格节点作为等值线追踪的基准点, 忽略了原始数据的空间结构特点, 精确表示元素含量的关键特征时较为困难, 从而导致等值线圈定的极值区与原始数据的极值点无法套合, 在地球化学图面上, 即呈现为元素浓集中心与极值点的空间位置不吻合(图1), 造成地球化学图件成果与实地调查情况不相符, 为地球化学异常的追踪、查证带来极大的困难, 甚至是误导。

图1 高值点与浓集中心偏移现象示意

为了避免Grid网格化过程中的精度损失, 往往采取另一种直接对原始采样点建网的常用网格化方法— — 不规则三角网。基于该方法进行离散点网格化, 网格点就是原始采样点本身, 减少了精度损失, 同时适用于各种数据分布密度和不规则形状区域[3]。然而, 作为TIN的基本单元, 三角形的几何形状直接决定着TIN的应用质量[4]。由于该方法绘制的等值线趋势易受病态三角形影响, 所以往往勾绘出的等值线不够圆滑美观[5]。除此之外, 按照地球化学勘查的要求, 地球化学图的成图范围或为以标准图幅为单位的梯形, 或为规则的矩形, 而不规则三角网法制作的等值线图边界为不规则凸包, 因此还需要对数据进行扩边处理[5]。如图2所示, 利用不规则三角网绘制的地球化学等值图中, 等值线形态不佳, 且成图边界与图框之间留有空白, 难以满足地球化学成果表达的需求。所以对离散点数据采用不规则三角网的方法来制作地球化学图, 虽然能够解决偏移问题, 但是因其不够圆滑及不能扩边的问题, 使得图面不够美观, 在地球化学图的编制过程中不能够被广泛应用。

图2 规则三角网绘制的地球化学图示意

针对上述问题, 众多学者提出了多种解决方法。宋敏和张见明等[6]采用矩形网格法绘制等值线, 在等值点的追踪过程中加密局部等值点, 并且在细分后的节点上重新计算高程值, 有效提高网格化精度, 但是浓集中心偏移的现象依旧存在。胡金虎[7]通过对原始TIN模型进行加密, 得到均匀分布的三角网格。王学春和尚继红[8]利用三次Bezier曲线拼接模型实现了完全满足拓扑关系的等值线光滑。边淑莉和柳佳佳[9]等则提出了基于规则格网DEM追踪等值线的改进算法。此外, 多位学者对基于TIN追踪等值线的算法进行优化[10, 11, 12], 虽然提高了制图可视化效果, 但是具体到中大比例尺化探制图工作中, 依然需要提高表达精度并解决扩边问题。

2 算法实现
2.1 算法流程

针对上文提到的传统网格化方法的诸多问题, 一个行之有效的思路是原始采样点集A与内插后得到的规则矩形网格点集B合并, 得到一个新的点集C, 然后对点集C构建不规则三角网并追踪绘制等值线。

点集C通过原始采样点标定元素值浓集中心位置, 提高等值线精度, 防止高值点和浓集中心偏移的现象出现; 通过分布均匀的矩形网格节点控制生成的三角形形状, 减少病态三角形的生成, 绘制的等值线更加圆滑美观; 同时, 规则矩形网格点的加入, 填补了原始采样点分布范围到图框边界之间的空白区域, 能够保证等值线图的边界与图框边界吻合。

除此之外, 为了减少病态三角形的生成, 笔者提供了两种改进策略:以极值点点集A'取代原始采样点集A, 与点集B合并; 删除点集C中易导致病态三角形生成的畸形网格节点。

图3 算法及其改进策略流程

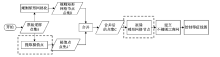
结合图3, 对基于极值点约束的离散数据场等值线生成算法绘制等值线图的完整流程详述如下。

(1)对原始采样点集A提取极值点, 得到极值点点集A'。

(2)对原始采样点集A进行规则矩形网格化, 得到规则矩形网格节点点集B。

(3)合并点集A'和点集B, 得到点集C。

(4)删除点集C中导致病态三角形生成的畸形网格节点, 得到点集D。

(5)利用点集D建立不规则三角网, 绘制等值线图, 绘制结束。

下面具体说明其中的关键步骤。

2.2 极值点提取

显而易见, 点集C中包含的原始采样点越多, 对矩形网格节点的均匀性破坏越大, 越容易形成病态三角形。因此, 为了减少病态三角形的生成, 采用以极值点点集A'取代原始采样点集A, 与点集B合并的策略。

极值点是指那些在局部邻域分析范围内, 比周围所有点的元素值高(或低)的采样点, 是最具控制性的特征点位[13]。对地球化学图而言, 极值点是位于最内层等值线所圈定的区域内的采样点的集合, 由此得到极值点集提取的方法, 具体如下:①对原始采样点点集A构建不规则三角网, 并制作地球化学等值线图; ②根据等值线与原始采样点的拓扑关系, 提取位于最内层等值线所圈定的区域内的采样点, 即为极值点点集A'。

由于利用不规则三角网追踪的等值线图不会产生浓集中心偏移的现象, 所以用该方法提取的极值点集满足算法需求。

2.3 畸形网格点剔除

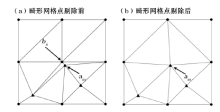
在点集合并之后, 如果直接对合并后的新点集C建立不规则三角网模型, 可能会因为规则矩形格网节点与原始采样点的距离过近, 导致最终的不规则三角网形状难以达到最优化[14, 15]。在此将与原始采样点距离过近的网格单元顶点称为畸形网格点。如图4a所示, 实心圆点bn为规则矩形网格节点, 三角形点am为原始采样点, 由于bn与am的距离过近, 导致以bnam为底边的两个三角形顶角过于尖锐, 势必会造成等值线局部曲率变化过大, 从而影响可视化效果。即使利用计算机图形学方法对等值线进行光滑处理, 但其本质也是以降低等值线的精度为代价, 而且处理效果往往不能达到预期。

图4 畸形网格点对三角形构网的影响

为了能够最大程度降低畸形网格点对三角网形态的影响, 可采取剔除畸形网格点, 保留原始采样点的策略(如图4b所示)。

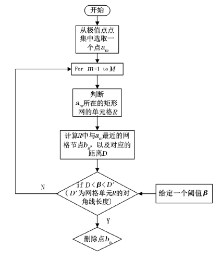
(1)已知点集C中, 来自规则矩形网格节点点集B的点的数量为N, 来自极值点点集A'的点的数量为M。

(2)对于来自极值点点集A'中的一点am, m∈ [1, M], 确定点am所在的矩形网的单元格R, 进而确定单元格R中距离点am最近的点bn, 且点bn来自规则矩形网格节点点集B, n∈ [1, N], 并通过以下公式计算点bn与点am的距离D:

D=(xbn-xam)2+(ybn-yam)2,

其中, xbn和ybn分别为点bn的x、y坐标, xam和yam分别为点am的x、y坐标。

(3)通过

D'=X2+Y2

计算网格R的对角线长度D', 其中, X和Y分别为规则矩形网格节点点集B中任意2个相邻点在x以及y方向上的点距。

(4)判断是否删除网格节点bn:给定阈值β , 若D< β < D' , 则删除节点bn; 否则保留。

(5)重复步骤(2)到步骤(4), 直到对极值点点集A'中的每个点判断一次是否删除最近网格节点, 最终剩下的所有点构成点集D。对应的算法流程如图5所示。

图5 畸形网格节点剔除算法流程

由图4b可以看出, 在剔除了畸形网格节点bn后, 重新构建的不规则三角网消除了图4a中以bnam为底边的尖锐三角形, 使得不规则三角网的形状更佳, 从而保证绘制的等值线更加圆滑美观。

3 实验与分析

实验采用冀东某地区1∶ 50 000水系沉积物离散采样点数据, 采样面积为460 km2, 采样平均密度为4个采样点/km2。为了验证方法的有效性, 分别

对实验数据进行以下处理:

(1)采用规则矩形网格法绘制等值线。内插采用距离反比加权(inverse distance weighting, IDW)算法, 网格间距设为0.5 km× 0.5 km, 四方向搜索, 最少有效搜索点数为5个。

(2)采用不规则三角网绘制等值线。采用Delaunay三角剖分算法建网, 保证三角网的形态最优。

(3)采用基于极值点约束的离散数据场等值线生成算法绘制等值线。通过处理(1)得到规则矩形网格节点, 将其与原始数据中的极值点集合并, 之后剔除畸形网格点, 并建立Delaunay三角网。

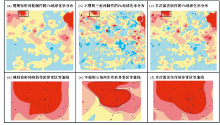
以0.1为等对数间隔, 利用以上三组网格数据绘制该地区的Pb地球化学图, 结果如图6所示。图中, 图6a、图6b、图6c分别为采用上述三种处理方式绘制的研究区域Pb地球化学图。选取图6a中该区域内极值点偏移现象比较明显的某处异常(异常范围由黑色矩形框标记), 将三幅Pb地球化学图中该范围同比放大显示(图6d、图6e、图6f), 对其进行整体和细节的对比。

就整体的可视化效果而言, 图6a和图6c中绘制的等值线更加圆滑美观, 极少出现局部曲率变化过大的曲线, 更加符合地球化学工作者的意愿。图6b中等值线形态不够美观且成图边界不规则, 无法满足地球化学勘查科研或生产的需要。

图6 三种不同方法制作的Pb等值线分布(· 代表原始采样点, ▲代表极值点)

然而, 在利用规则矩形网格制作的地球化学图中, 会出现元素浓集中心与极值点位置偏移的图面效果, 这种现象是不符合实际情况的。尤其当这种问题出现在地球化学元素异常区的时候, 将会给地化工作者带来极大不便甚至误导。图6d中, 极值点并未处于元素浓集区中心内, 而图6e和图6f中二者的位置是完全吻合的。实验表明, 应用本次算法制作的等值线图结合了规则矩形格网和不规则三角网二者的优点, 在保证可视化效果的同时, 提高了等值线图的精度。

4 结语

提出了一种基于极值点约束的离散数据场等值线生成算法, 通过原始采样点和规则矩形网格点合并点集, 有效地解决了地球化学图中元素浓集中心与极值点偏移的问题。实验结果表明, 采用该算法制作的等值线图, 在保证可视化效果的前提下, 提高了地球化学图的表达精度。

该方法提高了制图精度, 并达到了一定可视化美观程度, 但并未将所有的原始采样点纳入合并后的点集, 精度上仍有提高的空间, 同时在极值点附近, 元素的含量梯度可能会急剧变化, 从而形成紧密套合的多级闭合等值线。基于现存问题, 未来可进一步结合三角网加密技术, 继续深入研究中大比例尺地球化学图浓集中心偏移问题的解决方法。

The authors have declared that no competing interests exist.

参考文献
[1] 吕国安. 成矿区带地球化学异常评价方法[M]. 北京: 冶金工业出版社, 2002: 17-19. [本文引用:1]
[2] 韩小明, 张晓梅, 王瑞, 等. 地球化学等值线图生成方法研究及相关软件使用对比[J]. 新疆地质, 2007(3): 327-330. [本文引用:1]
[3] Wang Z W, Zhu C Q, Wang Y G. The reconstruction and applications of the contour lines based on TINs[C]// Proceedings of the 8th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences. Shanghai: 2008: 100-106. [本文引用:1]
[4] Sohler C. Fast reconstruction of delaunay triangulations[J]. ComPutationalGeometry, 2005, 31: 166-178. [本文引用:1]
[5] 王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009(4): 1327-1338. [本文引用:2]
[6] 宋敏, 张见明, 覃先云. 基于格网DEM的自适应等值线图及UG实现[J]. 微计算机信息, 2010(30): 181-182. [本文引用:1]
[7] 胡金虎. 基于不规则三角网的高精度等值线生成方法[J]. 工程勘察, 2011, (02): 64-68. [本文引用:1]
[8] 王学春, 尚继宏. 三次贝塞尔曲线拼接模型的折线式等值线曲线化应用[J]. 测绘科学, 2011(2): 192-194. [本文引用:1]
[9] 边淑莉, 柳佳佳, 王海龙, 等. 基于规则格网DEM的等高线提取算法的优化与实现[J]. 测绘科学. 2008(6): 151-153. [本文引用:1]
[10] 胡德鹏, 黄晓萍, 任年海. 基于不规则三角网(TIN)的追踪等值线算法及对等值线光滑算法的研究[J]. 计算机与信息技术, 2006(3): 46-48. [本文引用:1]
[11] 吴凡, 粟卫民, 杨英伟, 等. 基于联合Delaunay三角网的等高线地形特征提取研究[J]. 中国矿业大学学报. 2007, 36(2): 172-176. [本文引用:1]
[12] 郑春燕, 郭庆胜, 胡华科, 等. 基于约束Delaunay三角网建立等高线层次结构的方法[J]. 武汉大学学报: 信息科学版. 2008, 33(5): 524-527. [本文引用:1]
[13] 罗明良, 汤国安. 地貌认知及空间剖分的山顶点提取[J]. 测绘科学, 2010(5): 126-128 [本文引用:1]
[14] 陈仁喜, 龙毅. 顾及三角形处理的TIN建立算法[J]. 武汉大学学报: 信息科学版. 2003(5): 619-622. [本文引用:1]
[15] 徐道柱, 刘海砚. 大量约束边条件下Delaunay三角网的快速生成[J]. 测绘工程. 2007(3): 6-10. [本文引用:1]