作者简介: 李俊杰(1989-),男,江西上饶人,硕士,助理工程师,从事电法勘探无网格化正演研究工作。 Email:838885421@qq.com
无网格法作为一种新型数值方法,精度高、自适应分析容易,避免了复杂的网格生成过程,在计算力学领域应用广泛。尝试将无网格算法用于点源二维电场的计算,从点源二维变分问题出发代入移动最小二乘近似构造的形函数,推导了与之对应的无网格总体矩阵表达式并用含背景网格的高斯积分将其离散化;通过一个简单的二层模型算例验证了算法的正确性。
The mesh-free method, as a new numerical method which avoids the mesh generation and possesses the advantages of high precision and simple adaptive analysis, has been widely used in the field of computational mechanics. In this paper, the authors attempt to calculate the point source two-dimensional electric field by using mesh-free method. The moving least square approximation theory is introduced and stiffness matrix of mesh-free method is deduced into shape function structured by moving least squares approximation corresponding to the point source two-dimensional variational problem, and the expression is discretized by Gauss integral containing background grid. At last, the validity of the algorithm is verified by a simple calculation of two-dimensional model.
点源二维电场正演
笔者以点源二维电场问题为例介绍了无网格法的近似原理, 从点源二维变分问题出发结合无网格思想推导了总体矩阵的无网格化离散表达式, 并通过一个简单二层地质模型的计算验证了算法的有效性。
点源为三维源, 需先采用傅立叶变换将三维点源从空间域转化为波数域二维源, 当地下电性结构为二维时, 取走向为z轴, x轴与z轴垂直, y轴垂直向上, 求解域为矩形区域, 4个顶点依次以A、B、C、D逆时针编号, 波数域电位满足变分问题[14]:
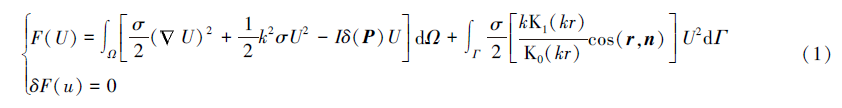
式中:▽是二维哈密顿算子, ▽=
无网格法利用位于积分点支持域内的场节点构造形函数, 用Galerkin法建立系统方程, 近似手段多采用移动最小二乘法, 其优点是能够通过权函数的适当选取来得到具有高阶连续性的形函数, 系统矩
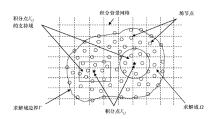
阵表达式中包含的积分可采用含背景网格的高斯积分求解。图1为无网格法背景网格、支持域、积分点与场节点示意。
由于背景网格的积分常选用高斯积分法, 故积分点又称高斯积分点或高斯点, 对于节点均匀分布的情况支持域尺寸一般取横、纵向节点间距与支持域无量纲尺寸之积, 本文中支持域无量纲尺寸α =1.0。
将变分符号代入式(1), 代入MLS构造的的形函数
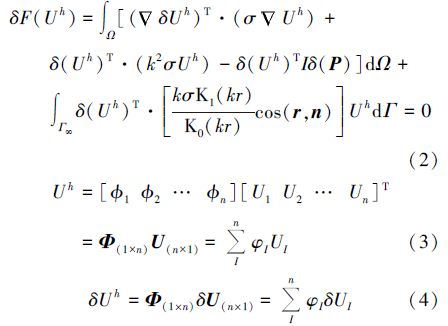
式中:Φ 为形函数矩阵; n为支持域内的节点数; U为支持域内n个节点的场向量。将式(3)、式(4)代入式(2), 有
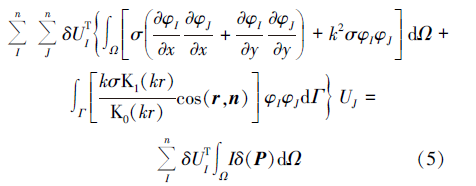
式(5)采用支持域内n个场节点编号, 对于求解域内所有场节点还应有一个用于将局部节点矩阵组装成总体刚度矩阵的总体编号体系。当节点I和节点J位于不同支持域时, 其相应的被积函数为零, 因此可得到按求解域节点编号的总体编号体系方程
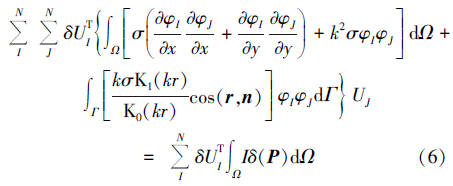
式(6)右端的积分代表点源对二维电场的贡献, δ 函数积分存在式(7)的数值解
式中x0与y0为点源P所在位置的坐标, 将式(7)代入式(6)得
由于δ UT是任意的, 故式(8)成立的条件为
式(9)即为无网格法构造的系统方程。由于求解域为矩形, 具体计算时应先将K包含的无穷边界积分项展开成
式中r=
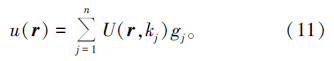
| 表1 最优化波数 |
K的表达式中包含对求解域Ω 与求解域边界Γ 的积分, 为计算这些积分, 须将求解域离散成一组背景网格(图1), 总体积分可表示成这些单元积分之和的形式, 每个单元的积分利用高斯积分法求解:
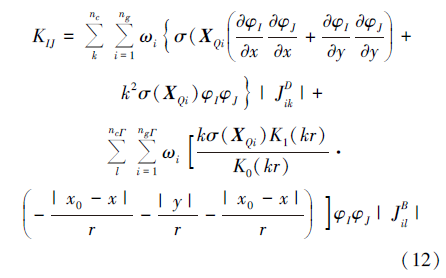
式中:nc与ncΓ 分别为背景单元及边界单元的个数; ng与ngΓ 分别为背景单元及边界单元内的高斯点数目, 本文中每个背景单元采用4(2× 2)个高斯点, 每个边界单元采用2个高斯点; ω i为第i个高斯点XQi的权系数;
点源二维问题数值计算精度一般受求解域大小、场节点分布方式及最优化波数的选取控制, 影响因素较为复杂。不同电极距的计算往往涉及节点的重新分布, 节点的变动有时会导致较差的计算效果。本文旨在介绍二维变分问题的无网格解法, 故先以单个电极距(r=1 m)的计算来验证算法的正确性, 影响无网格法求解精度的因素仍需进一步研究。
研究一个二层介质模型:第一层电阻率ρ 1=1 Ω · m, 层厚h1=2 m; 第二层电阻率ρ 2=19 Ω · m。表2为该模型在偏移距r=1 m处的计算电位值。
| 表2 r=1 m时模型不同数值方法的电位计算结果 |
(1) 将无网格算法应用于点源二维问题的正演计算, 简述了无网格法基本原理。
(2) 从点源二维变分问题出发, 代入无网格法构造的形函数, 推导了点源二维波数域电位的总体矩阵的表达式, 均匀半空间模型电位的数值计算验证了无网格算法的正确性, 其计算精度与有限元法双二次插值相当。
由于场源点是奇异点, 在点源附近随着r的增大电位衰减很快, 因此r较小时双二次插值的精度高于线性插值。表2显示无网格法计算结果与有限元双二次插值相当。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|