等效偏移距在垂直地震剖面中的研究及应用

引用本文

孙乃泉, 陈占国. 等效偏移距在垂直地震剖面中的研究及应用[J]. 物探与化探, 2015,39(3): 589-594.
SUN Nai-Quan, CHEN Zhan-Guo. The study and application of equivalent offset migration of VSP[J]. Geophysical and Geochemical Exploration, 2015,39(3): 589-594.
Doi:10.11720/wtyht.2015.3.26 复制到剪切板

Permissions

《物探与化探》编辑部

等效偏移距在垂直地震剖面中的研究及应用

孙乃泉¹, 陈占国²

1.长安大学地质工程与测绘学院,陕西西安 710054

2.中国石化石油物探技术研究院,江苏南京 211103

作者简介: 孙乃泉(1977-),男,黑龙江哈尔滨人,博士,主要从事地震资料特殊处理及解释方面研究。

收稿日期: 2014-09-11

基金: 国家自然科学基金项目(41074089)

摘要

基于散射理论的等效偏移距方法在地震资料数据处理中具有独特的优势,尤其在速度分析和偏移成像方面。笔者将该理论应用到垂直地震剖面(VSP)数据处理中,研究了基于该理论的VSP数据共散射点道集的形成方法,并试验了VSP共散射点道集在速度分析和成像方面的应用效果。理论模型和实际资料测试结果表明,该方法能方便有效地为VSP提供不受初始速度和地层倾角影响的有效偏移速度,除了能在常规成像方法的成像区域内准确成像外,还能在常规成像方法的盲区外有效成像,在一定程度上扩大了VSP方法的成像范围,具有有较好的研究意义和应用前景。

关键词: 等效偏移距; 垂直地震剖面; 速度分析; 偏移成像

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)03-0589-06

The study and application of equivalent offset migration of VSP

SUN Nai-Quan¹, CHEN Zhan-Guo²

1.College of Geology Engineering and Geomatics,Chang'an University,Xi'an 710054,China

2.SINOPEC Geophysical Research Institute,Nanjing 211103,China

Abstract

The concept of equivalent offset migration (EOM) method is introduced to vertical seismic profile (VSP) in the paper.The definition of the VSP equivalent offset migration and data processing method based on VSP equivalent offset migration method are also introduced.The EOM method,which has particular advantages in velocity analysis and imaging,provides ideas for VSP scattered wave imaging and velocity analysis.The results of theoretic test and analysis of real data show that the VSP equivalent offset migration method is effective and feasible, and has the prospect of study and application.

Keyword: equivalent offset migration; vertical seismic profile; velocity analysis; migration imaging

Show Figures

Bancroft和Geiger等人^{[1, 2, 3, 4]}最早提出了等效偏移距(equivalent offset migration, EOM)的概念。这种方法建立在散射波理论和克希霍夫叠前时间偏移原理上, 它将地震散射波的双平方根旅行时公式用一个等效偏移距的概念转换成了单平方根公式, 在转换后没有发生数据时移。Fowler^[5]证明双平方根方程可以简化成多种双曲线形式, 但EOM方法是唯一没有引起时间改变的转换方法。因此, 我们可以利用等效偏移距将所有输入的地震道采样点以散射点为中心, 映射在给定的等效偏移距道上, 这个道集称为共散射点(CSP)道集。CSP道集聚集了所有可能的散射能量, 它具有更高的覆盖次数和更大的偏移距范围^[6]。其时距关系符合双曲线规律, 而且其速度分析结果不受地层倾角的影响^{[7, 8]}。

在地面地震中, 等效偏移距方法的应用比较成熟, 尤其对复杂地质条件下的低信噪比资料的速度分析和成像有独特的优势^[9]。笔者利用地面等效偏移距方法原理, 研究了VSP的等效偏移距方法, 并通过它进行VSP速度分析和成像应用, 从而为VSP的速度分析和成像提供一种新的途径。

1 VSP的等效偏移距

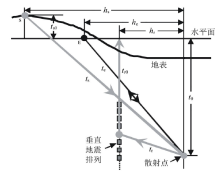
将地面地震等效偏移距的定义CSP道集^[10]引入到垂直地震剖面(VSP)中。考虑到接收方式的特殊性, 引入一个从井中接收点到基准面的虚拟垂直单程旅行时 $\begin{matrix} {t_{r 0}}^{[11]} \end{matrix}$ , 将地表震源处到散射点再到井中接收点, 以及井中接收点到基准面的旅行时之和作为VSP记录的总射线旅行时(图1), 这个关系表示为

$\begin{matrix} \begin{matrix} t = {[(t_{0} + t_{s 0})^{2} + (h_{s} / v_{s})^{2}]}^{\frac{1}{2}} + \\ {[(t_{0} - t_{r 0})^{2} + (h_{r} / v_{r})^{2}]}^{\frac{1}{2}} + t_{r 0}, (1) \end{matrix} \end{matrix}$

式中:h_s和h_r分别是地面震源和井中接收点到散射点的水平距离, v_s和v_r分别是地面震源和井中接收点到散射点的均方根速度, t₀是基准面到散射点的单程垂直旅行时, t_s0是地表震源到基准面的单程垂直旅行时; t_s0是带有符号的, 高于基准面取正, 低于基准面取负; t_r0始终为正, 且对井中每一个接收道来说, t_r0是常量, 如果基准面选在零偏移距震源高程面上时, 则t_r0就是零偏移距记录的直达波走时。

	Figure Option View Download New Window
	图1 VSP的等效偏移距定义示意

引入等效偏移距的概念后VSP记录的等效偏移距公式可以写成

$\begin{matrix} \begin{matrix} {[(t_{0} + t_{s 0})^{2} + (h_{s} / v_{s})^{2}]}^{\frac{1}{2}} + t_{r 0} + \\ {[(t_{0} - t_{r 0})^{2} + (h_{r} / v_{r})^{2}]}^{\frac{1}{2}} = 2 {[t_{0}^{2} + (h_{ε} {/ v)}^{2}]}^{\frac{1}{2}} 。 (2) \end{matrix} \end{matrix}$

VSP的等效偏移距的显式表达式为

$\begin{matrix} h_{ε} = v_{ε} {[t^{2} / 4 - t_{0}^{2}]}^{\frac{1}{2}}, (3) \end{matrix}$

式中:v_ε是散射点到基准面的均方根速度。v_s和v_r可以用v_ε表示为

$\begin{matrix} \begin{matrix} v_{s} = {(\frac{t_{0} v_{ε}^{2} + t_{s 0} v_{s 0}^{2}}{t_{0} + t_{s 0}})}^{\frac{1}{2}}, (4) \\ v_{r} = {(\frac{t_{0} v_{ε}^{2} + t_{r 0} v_{r 0}^{2}}{t_{0} + t_{r 0}})}^{\frac{1}{2}}, (5) \end{matrix} \end{matrix}$

式中:v_s0为地表震源处的近地表速度, v_r0为井中接收点到基准面的均方根速度。

2 VSP共散射点道集的映射方法

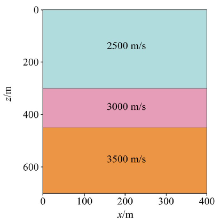
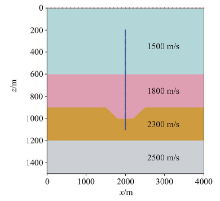
依据VSP的等效偏移距定义公式, 可以将VSP记录映射到CSP道集中。公式(2)的应用前提是需要知道速度参数。由于在地面地震中CSP道集对速度参数不敏感^{[12, 13]}, 在VSP中CSP道集也满足这一性质。图2是一个两层水平层的速度模型, 图3是该模型的VSP记录在不同速度误差下的抽取的某一个CSP道集。从道集可以看到, 在速度误差从50%变化到150%时, CSP道集的两组同相轴曲率以及同相轴对应的t₀时间都没有发生变化, 变化的只是同相轴有效数据的的偏移距范围。因此在VSP的CSP道集初次形成时, 可以通过现有的常规VSP速度分析手段提供初始速度v_ε。

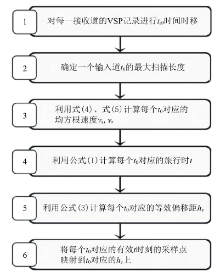
同时注意到, 公式(2)中引入了t_r0时间, 因此需要先对每一道VSP记录进行t_r0时间的静校正时移, 使记录满足公式走时关系。在公式(3)中h_ε是t₀的函数, 对于给定的输入道和指定的CSP道集, 在t₀值确定后, 初始速度v_ε是确定的, t可以通过式(1)计算得到。式(1)中的速度v_s和v_r可以借助均方根速度v_ε通过式(4)、式(5)分别计算得到。因此可以用t₀时扫描的办法将一个输入道映射到一个CSP道集上, 主要流程见图4。

	Figure Option View Download New Window
	图2 水平层状模型

	Figure Option View Download New Window
	图3 不同初始速度误差的CSP道集(从左到右速度误差分别为50%、80% 、100%、120%和150%)

	Figure Option View Download New Window
	图4 VSP共散射点道集的映射流程

3 VSP共散射点道集的速度分析

从形式上看, VSP的共散射点道集是双曲线, 它的时距关系与界面倾角无关, 只与散射点位置有关, 因此可以对形成的CSP道集像地面地震速度扫描一样进行速度分析, 得到的速度v就是偏移速度。在CSP道集映射过程中, 由于初始速度是由其他常规速度分析方法获得, 因此在用初始速度形成CSP道集后首先进行速度分析, 用更新的速度, 重新抽取CSP道集, 然后再次速度分析, 这样迭代速度分析直到达到成像速度精度的要求即可, 经验证明, 一般迭代两到三次即可。

4 VSP共散射点道集的成像

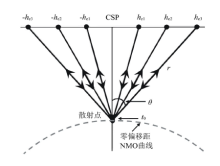
根据等效偏移距原理, 形成的CSP道集是满足双曲线形式的共成像点道集, 所以CSP道集成像方法的思路是对每个CSP道集沿双曲线轨迹应用Kirchhoff积分公式做保幅叠加, 这个过程相当于做动校正和叠加。具体做法如图5, 对于一个CSP道集, 对每一个成像点t₀(或z₀), 沿双曲线轨迹, 将每个等效偏移距道的能量乘以倾斜因子cosθ 和球面扩散因子vr^1/2(2D)后叠加到输出道的t₀时刻。在所有t₀时刻叠加完之后再对输出道以滤波因子ρ (t)进行褶积滤波即可, 其中θ 是z₀点与等效点的连线与垂直方向的夹角, r是z₀点与等效点的距离。

	Figure Option View Download New Window
	图5 等效偏移距偏移原理

5 模型测试

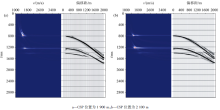
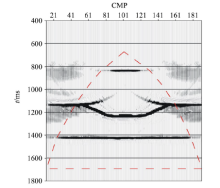
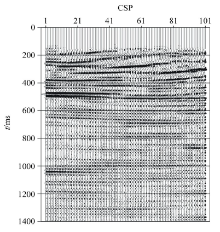
如图6, 是一个带有地堑构造的层状模型, 各层速度逐层递增。炮点范围0~4 000 m, 炮间距100 m。接收点深度200~1 100 m, 道间距10 m。图7是合成的其中一炮上行P波的记录。CSP道集抽取参数为:CSP范围1 000~3 000 m, 间距10 m, 最大等效偏移距2 000 m, 等效偏移距间隔10 m。图8是抽取的部分CSP道集和对应的速度谱(CSP点位置为1 900 m, 2 100 m), 从CSP道集上看, 道集形式和CMP道集类似都是双曲线形式, 三个双曲同相轴分别对应着三组地层, 而且道集覆盖次数很高(最大能达到200次, 对于一般的VSP道集来说, 是无法达到这么多的覆盖次数)。在速度谱上三个同相轴的速度能量聚焦的比较集中, 可以容易拾取各层的均方根速度。图9是通过VSP等效偏移距方法对模型数据成像的结果。成像的结果和模型构造是吻合的, 较清晰的呈现出了上下两层水平界面和中间的一个地堑构造。

为了与常规成像方法比较, 图10给出了Kirchhoff偏移成像结果, 比较两种结果, 在井附近反射波覆盖的区域里(红色线框示意区域, 也是VSP-CDP成像区), 两种成像方法的结果都能清晰且正确成像, 成像效果基本一致。在离井较远的低反射覆盖或无反射覆盖的区域, 本成像方法虽然有一定的偏移噪音, 但是构造的轮廓基本清晰呈现, 而Kirchhoff方法在反射成像区域外, 地堑构造两侧的地层虽也正确成像, 但也有一定的噪音, 同时在第一层水平层的成像中, 反射区外根本没有成像。因此, 通过比较可以看到, VSP的CSP道集成像, 在反射波覆盖区域内, 成像效果和常规方法不相上下上下, 而低反射波或无反射波区域内, 等效偏移距方法依然能够正确成像, 在一程度上扩大VSP的成像范围。

	Figure Option View Download New Window
	图6 地堑构造模型

	Figure Option View Download New Window
	图7 地堑构造模型单炮上行P波记录(炮点位置3 900 m)

	Figure Option View Download New Window
	图8 地堑构造模型部分CSP道集和速度谱

	Figure Option View Download New Window
	图9 地堑构造模型的CSP道集成像结果

	Figure Option View Download New Window
	图10 地堑构造模型的Kirchhoff偏移成像结果

6 实际资料测试

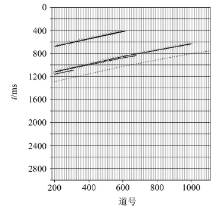
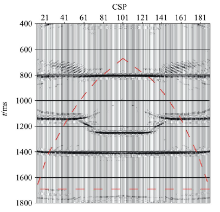
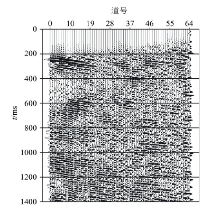
图11显示的是某WalkAway VSP的其中一炮上行P波记录, 该VSP记录总共25炮, 炮点偏移距范围0~1 000 m, 40 m炮间距。64道接收, 接收点深度300~930 m, 10 m道间距。CSP抽取参数:CSP范围0~500 m, 间距5 m, 最大等效偏移距1 000 m, 等效偏移距间隔20 m。图12是形成的部分CSP道集和对应速度谱(CSP位置100 m, 200 m), 可以看到, CSP道集覆盖次数较高, 浅层的同相轴很清晰; 同时, 能量谱上能看到清楚的能量团, 对应着CSP道集上的相应同相轴。图13是对实际资料的CSP道集等效偏移距偏移的结果。与一般的VSP成像结果比较, 该成像剖面成像范围很大, 但是和模型资料一样, 在远离井口的方向(CSP大号方向), 浅层的同相轴明显的失真, 出现上翘的现象, 这个原因一方面是由VSP记录炮点和接收点严重的不对称性造成的, 在这些地方, 共散射点道集的叠加不能使远散射点能量被完全抵消掉, 另一方面, 观测系统炮数较少, 偏移距较小, 此区域属于反射波盲区, 理论上等效偏移距方法可以在此区域成像, 但是不利的观测系统, 使远散射点能量强于近散射点能量。因此在造成浅层远离井的剖面上偏移噪音严重, 建议在观测系统设计时, 适当增大炮点偏移距, 增加炮点数量来改善浅层的成像效果。

	Figure Option View Download New Window
	图11 实际资料的上行P波记录

	Figure Option View Download New Window
	图12 实际资料的CSP道集和速度谱

	Figure Option View Download New Window
	图13 实际资料的CSP道集成像结果

7 结论

通过VSP的等效偏移距方法原理, 以及模型资料和实际资料的实验处理可以看到, 等效偏移距方法将VSP记录映射成的共散射点道集, 与地面记录的共散射点道集一样, 是一种完全的双曲线形式的道集, 具有较高的覆盖次数和较大的偏移距范围, 通过这种道集可以进行和地面地震一样的速度分析和成像。其速度分析的结果不受地层倾角的影响, 可以为后续的偏移成像直接提供偏移速度; 其成像过程是叠前偏移的过程, 而且成像结果在常规成像方法的成像区域内, 成像效果和常规方法基本一致, 在常规成像方法的成像区域外也能较好的成像, 但同时还存在一定的噪音干扰, 因此, 如何有效的压制噪音干扰是本方法今后亟需解决的问题之一。总之, 基于等效偏移距原理的VSP速度分析和成像方法, 不失为VSP记录的速度分析和成像提供了一种新方法和途径。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Bancroft J C, Geiger H D. Equivalent offsets and CRP gathers for prestack migration[C]//Expand ed Abstracts of 64^thSEG Annual International Meeting, 1994: 672-675. [本文引用:1]
[2]	Bancroft J C, Geiger H D, Foltinek D, et al. Prestack migration by equivalent offsets and CSP gathers[J]. CREWES Report, 1994, 6(27): 1-18. [本文引用:1]
[3]	Bancroft J C, Geiger H D, Wang S W, et al. Prestack migration by equivalent offsets and CSP gathers: an Update[J]. CREWES Research Report, 1995, 7(27): 1-10. [本文引用:1]
[4]	Bancroft J C, Wang S, Foltinek D S, et al. Common scatter point (CSP) prestack migration[C]//National Convention: Expand ed Abstracts CSEG, 1995. [本文引用:1]
[5]	Flower J C. A comparative overview of prestack time migration methods[C]//Expand ed Abstracts of 66^th SEG Annual International Meeting, 1996: 1571-1574. [本文引用:1]
[6]	秦宁, 李振春, 杨晓东, 等. 叠前多级优化联合偏移速度建模[J]. 地球物理学进展, 2013, 28(1): 320-328. [本文引用:1]
[7]	斯兴焱, 李录明, 胥良君, 等. 三维VSP多波速度分析方法及应用[J]. 石油物探, 2012, 51(1): 56-64. [本文引用:1]
[8]	刘玉金, 李振春, 黄建平, 等. 绕射波叠前时间偏移速度分析及成像[J]. 地球物理学进展, 2013, 28(6): 3022-3029. [本文引用:1]
[9]	李战业, 尹军杰, 王赟. 地震散射波模拟成像在金属矿勘探中的应用[J]. 地质与勘探, 2009, 45(2): 80-84. [本文引用:1]
[10]	王伟, 尹军杰, 刘学伟, 等. 等效偏移距方法及应用[J]. 地球物理学报, 2007, 50(6): 1823-1830. [本文引用:1]
[11]	Bancroft J C, Xu Y. Equivalent offset migration for vertical receiver arrays[C]//Expand ed Abstracts of 69^th SEG Annual International Meeting, 1999. [本文引用:1]
[12]	Bancroft J C. Velocity sensitivity for equivalent offset in CSP gathers[C]//CREWES Research Report, 1995. [本文引用:1]
[13]	陈占国. 地震散射波成像方法研究[D]. 西安: 长安大学, 2012: 52-53. [本文引用:1]

1994

0.0

... Bancroft和Geiger等人^[1,2,3,4]最早提出了等效偏移距(equivalent offset migration,EOM)的概念 ...

1994

0.0

... Bancroft和Geiger等人^[1,2,3,4]最早提出了等效偏移距(equivalent offset migration,EOM)的概念 ...

1995

0.0

... Bancroft和Geiger等人^[1,2,3,4]最早提出了等效偏移距(equivalent offset migration,EOM)的概念 ...

1995

0.0

... Bancroft和Geiger等人^[1,2,3,4]最早提出了等效偏移距(equivalent offset migration,EOM)的概念 ...

1996

0.0

... Fowler^[5]证明双平方根方程可以简化成多种双曲线形式,但EOM方法是唯一没有引起时间改变的转换方法 ...

2013

0.0

... CSP道集聚集了所有可能的散射能量,它具有更高的覆盖次数和更大的偏移距范围^[6] ...

2012

0.0

斯兴焱, 李录明, 胥良君, 等. 三维VSP多波速度分析方法及应用[J]. 石油物探, 2012, 51(1): 56-64.

针对三维VSP多波速度分析问题,研究并实现了三维VSP上行反射纵波及转换波的速度分析方法.该方法可求取接收点以下反射层的多波速度,填补了常规VSP速度分析方法中仅依靠下行波初至求取接收点以上地层速度的缺陷.该速度分析方法包含非零偏VSP多波时距曲线公式、纵波反射点计算、转换波转换点的迭代算法及在没有横波初至信息的情况下求取检波点处横波速度的方法.在此基础上,建立了三维VSP多波速度分析流程和步骤.应用于理论VSP多波资料及实际斜井三维VSP多波资料的处理,得到了与地面地震时间坐标一致的多波叠加速度模型、多波动校正道集及叠加剖面.处理结果证明了该方法的正确性和有效性.

... 其时距关系符合双曲线规律,而且其速度分析结果不受地层倾角的影响^[7,8] ...

2013

0.0

刘玉金, 李振春, 黄建平, 等. 绕射波叠前时间偏移速度分析及成像[J]. 地球物理学进展, 2013, 28(6): 3022-3029.

The important heterogeneous objectives of structural and lithologic interpretation, such as faults, salts, karst caves and fractures et al , usually act as extremely complex diffractions on the seismic record. Therefore, it's very important to correctly identify and image diffractions for hydrocarbon exploration and production. However, high-resolution information, encoded in diffracted waves, is generally lost during conventional seismic data processing workflow and imaging methods, which incline towards reflections. We propose here method to extract diffractions from total wavefield by plane wave destructor based on the differences of time distance curve in the simulated plane wave sections. After extraction, prestack time migration velocity analysis and imaging method based on common scattering-point gathers is used to obtain reliable root-mean-square velocity field and high resolution imaging result specific to diffractions. The synthetic example of 2-D SEG/EAGE salt demonstrates that the proposed method is effective and applicable.

1. College of geosciences, China University of Petroleum (East China), Qingdao 266555, China; 2. Geophysical Research Institute, BGP Inc., CNPC, Zhuozhou 072751, China

断层、盐丘、溶洞、裂缝等非均质体作为现阶段构造、岩性解释的重要目标，在地震记录上多表现为极其复杂的绕射波响应特征，正确识别和成像绕射波对油气勘探开发具有十分重要的现实意义.然而，常规的处理流程和成像方法都是针对反射波而言的，会在一定程度上压制携带高分辨率信息的绕射波波场，针对这一问题，本文根据绕射波和反射波在合成平面波记录上的时距曲线差异，采用平面波解构滤波器(PWD)从全波波场中提取出绕射波波场，然后采用基于共散射点道集(CSP)的叠前时间偏移方法，充分利用绕射波波场的信息，不仅可以得到较为可靠的均方根速度场，而且可以改善特殊地质体的成像效果.二维SEG/EAGE盐丘模型处理表明，本文提出的方法正确有效，具有一定的应用价值.

... 其时距关系符合双曲线规律,而且其速度分析结果不受地层倾角的影响^[7,8] ...

2009

0.0

李战业, 尹军杰, 王赟. 地震散射波模拟成像在金属矿勘探中的应用[J]. 地质与勘探, 2009, 45(2): 80-84.

Abstract:The seismic data collected during the base metal exp loration can be hampered by a variety of non - reflecting signals because of the hetero2geneity of ore bodies and host rocks. It is difficult to p roduce a high - quality seismic p rofile when conventional seismic p rocessing algorithms are app liedto the data. According to the Huygens - Fresnel p rincip le, every grid node can be considered as a vibrating source, and geologicalmodel can be discretewithin the grids. Therefore we have stacked all kinds of waves, including scattered waves from these grids. It seems that the more scattered signals areused and the better themigrated section is. Two geologicalmodels are simulated and tested, one is the Tongling coppermine in the eastern China, and an2other is Gejiu tin mine in Yunnan Province of the south - western China. We have simulated the seismic scatteringwave generated high - qualitymigratedseismic p rofiles, which match the geologicalmodels verywell. It p roves that imaging of the seismic scattered wavemay be an app rop riate tool to p rocess theseismic data in base metal exp loration

[摘要]由于金属矿地质模型一般具有强非均匀性,造成金属矿地震勘探中采集到的信号杂乱,应用常规的反射地震处理技术难以获得可靠的成像效果。而基于惠更斯%菲涅尔原理的散射成像方法能充分利用地震信号中的全波场信息,例如反射波、绕射波、回转波、直达波、转换波等,它们都是散射波的一种表现形式,从而可以获得较好的成像效果。结合中国东部典型铜矿- 铜陵冬瓜山铜矿与中国西部典型锡矿- 云南个旧锡矿的地质模型,我们模拟了散射波地震记录,并通过散射成像方法获得了高质量的偏移结果,从数值模拟角度证明了散射成像在金属矿地震勘探中具有较好的应用前景。

... 在地面地震中,等效偏移距方法的应用比较成熟,尤其对复杂地质条件下的低信噪比资料的速度分析和成像有独特的优势^[9] ...

2007

0.0

王伟, 尹军杰, 刘学伟, 等. 等效偏移距方法及应用[J]. 地球物理学报, 2007, 50(6): 1823-1830.

When the geologic structure is complex, the dip of the layer is large, or the lateral change of lithology is abrupt, the reflection waves are weak with a low signalnoise ratio, even unable to be received. Routine imaging method is invalid for such data, but the equivalent offset migration based on scattered waves is viable. The method consists of two steps: the first is a gathering pro cess that forms common scatter point gathers; the second is a focusing process that applies a simplified Kirchhoff migration on the CSP gathers. Based on examples of numerical simulating and sea data, the paper shows that the method of scattering image is widely and practicably valuable in processing of complicated geologic structure and low signalnoise ratio seismic data.

1 Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing 100085, China;2 Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;3 China University of Geosciences, Beijing 100083, China

当勘探目标地质构造复杂、地层倾角较陡或岩性横向突变时，在地表接收到的反射信号较弱、信噪比较低，甚至接收不到反射波，常规偏移成像方法对这类数据很难精确成像，因此可以考虑基于散射理论的等效偏移距方法来成像.该方法分两步进行：第一步是抽取共散射点道集；第二步是对共散射点道集进行克希霍夫积分偏移.文中数值模拟及实际资料的实例表明，该方法在复杂地质目标及低信噪比地震资料的成像处理中具有一定的实用价值.

... 1 VSP的等效偏移距将地面地震等效偏移距的定义CSP道集^[10]引入到垂直地震剖面(VSP)中 ...

1999

0.0

1995

0.0

... 由于在地面地震中CSP道集对速度参数不敏感^[12,13],在VSP中CSP道集也满足这一性质 ...

2012

0.0

... 由于在地面地震中CSP道集对速度参数不敏感^[12,13],在VSP中CSP道集也满足这一性质 ...