一种新型有限差分网格剖分方法在大地电磁一维正演中的应用

引用本文

张辉, 唐新功. 一种新型有限差分网格剖分方法在大地电磁一维正演中的应用[J]. 物探与化探, 2015,39(3): 562-566.
ZHANG Hui, TANG Xin-Gong. The application of a new mesh generation method for finite difference to MT 1D inversion[J]. Geophysical and Geochemical Exploration, 2015,39(3): 562-566.
Doi:10.11720/wtyht.2015.3.21 复制到剪切板

Permissions

《物探与化探》编辑部

一种新型有限差分网格剖分方法在大地电磁一维正演中的应用

张辉^1,², 唐新功^1,²

1.油气资源与勘探技术教育部重点实验室(长江大学),湖北武汉 430100

2.长江大学地球物理与石油资源学院,湖北武汉 430100

通讯作者: 唐新功(1968-),男,教授,博士生导师。E-mail:tangxg@yangtzeu.edu.cn

作者简介: 张辉(1988-),男,长江大学在读硕士研究生,研究方向为电磁勘探。E-mail:xxx.zhanghui@qq.com

收稿日期: 2014-08-11

基金: 国家自然科学基金项目(41274115,41274082); 国家重点基础研究发展计划(973计划)项目(2013CB228605); 中石油创新基金项目(2013D-5006-0302)

摘要

介绍了有限差分算法在大地电磁测深法中的应用,推导了一维层状介质和连续介质模型下的有限差分算法,提出了一种新的网格剖分方法,并通过两层和三层介质模型的正演计算,验证了算法的正确性以及网格剖分方法的合理性。设计了一种连续介质模型,与两种不同程度近似的多层层状介质模型进行了正演结果的对比,指出了研究连续介质模型正演的必要性。对于连续介质模型,计算中剖分得越详细,其结果越接近真实值,而随着误差的逐渐减小,精确度的提高不再明显,但资源与时间的消耗将大幅增加。因此,无限制地减小网格步长是不必要的。同时,为了兼顾误差大小与网格步长的关系,采用了一种将一次网格剖分进行二次差分计算的方法得到新的结果,使计算结果明显得到了改善。

关键词: 大地电磁; 有限差分; 一维正演; 连续介质; 网格剖分方法

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)03-0562-05

The application of a new mesh generation method for finite difference to MT 1D inversion

ZHANG Hui^1,², TANG Xin-Gong^1,²

1. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Yangtze University, Wuhan 430100, China

2. Department of Geophysics and Petroleum Resource, Yangtze University, Wuhan 430100, China

Abstract

This paper describes the application of finite difference algorithms in MT method, deduces the algorithms of 1D layered and continuous medium, and proposes a new mesh generation method. Meanwhile, with two-layer or three-layer medium model inversion calculation, the paper demonstrates the correctness of the algorithms and rationality of the grid subdivision method. The authors also designed a kind of continuous medium and made a comparison of the inversion result between two kinds of multiple layered medium models which have different layer approximations, and indicated the necessity of continuous medium model inversion research. For continuous medium model, the fine the grid, the better the approach result. Nevertheless, with the gradual decreasing of the error, the improvement of accuracy becomes not so distinct. However, resource and time consumption will dramatically increase. So decreasing grid spacing without restriction is not necessary. What's more, taking both the error and grid spacing into consideration, the authors conducted second difference calculation in first mesh generation and achieved a new conclusion, which can distinctly improve the calculation result.

Keyword: finite difference; MT; 1D inversion; continuous medium; new mesh generation method

Show Figures

大地电磁测深法(MT)是利用天然的大地电磁场作场源, 探测地下电性结构, 研究地质构造的一种电磁测深方法。当天然交变电磁场以平面波的形式垂直入射大地时, 由于电磁感应现象, 地面上电磁场观测值将包含有地下电阻率的分布信息。不同频率的电磁波, 可以穿透的地层深度不同。因此, 研究大地对电磁场的频率响应, 可以获得地下不同深度介质电阻率的信息^[1]。

目前, 大地电磁测深数值模拟的主要方法有有限差分法、有限单元法和积分方程法。三种方法各有其优缺点, 而有限差分法作为一种经典的数值模拟方法, 依靠其相对简单的理论基础及简便的计算过程, 在地球物理工作中应用非常广泛^[2]。其基本思想是把连续的定解区域用有限个离散点构成的网格来代替, 将每一处导数用有限差分近似公式代替, 从而把求解偏微分方程的问题转换成求解代数方程的问题。

早在70年代初期, Jepsen就对有限差分法电阻率正演数值模拟进行了详细论述^[3], Mufti采用非均匀网格剖分方式达成了以较少节点获得较高精度的目的^[4]。从80年代开始, 周熙襄、罗延钟等地球物理工作者为有限差分法在国内的发展做出了非常大的贡献 $\begin{matrix} ^{[57]} \end{matrix}$ 。而到了现代, 有限差分法更是得到了极大的发展, 几乎运用到了电法勘探的各个分支当中, 成为一种最基本、最有效的数值模拟方法 $\begin{matrix} ^{[810]} \end{matrix}$ 。

在有限差分法的发展过程中, 计算精度与计算速度一直是所有研究者致力改进的方向。传统的有限差分法网格剖分方式, 网格步长都是固定不变的, 但这种算法在某些情况下缺乏足够的稳定性^[11]。在大地电磁测深法中, 由于天然电磁波具有很宽的频谱, 不同频率的电磁波衰减快慢大大不同。若将传统的网格剖分方式运用到大地电磁测深法有限差分法中, 固定的网格步长, 对于衰减极快的高频电磁波, 很容易造成采样的不足; 而对于衰减极慢的低频电磁波, 又会出现过采样的情况。要想使全频率域都达到理想的计算精度, 传统的做法必须要对任一频率都采用很小的网格步长, 而这样做却极大地损失了计算速度, 同时也造成了存储资源的浪费。

因此, 有限差分法运用在大地电磁正演中时, 是不宜采用传统的网格剖分方式的。这种不足, 可以通过可变步长的网格剖分方式加以改进。本文将以一维层状介质和连续介质为例对此问题进行分析和讨论。

1 有限差分格式推导

根据大地电磁测深理论, 一维介质中电磁场满足的微分方程为^[12]:

$\begin{matrix} \frac{\partial^{2} E_{x}}{\partial z^{2}} + iωμ σ_{z} E_{x} = 0 (1) \end{matrix}$

式(1)中, σ _z为深度h=z时的地层电导率。

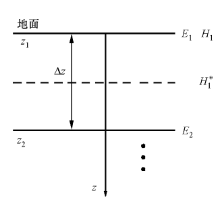
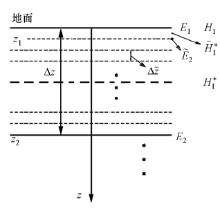
应用有限差分方法对地电模型进行网格剖分, 如图1所示。图中, z₁、z₂、z₃、…、z_n为网格节点, E₁、E₂、E₃、…、E_n和σ ₁、σ ₂、σ ₃、…、σ _n分别为各节点处的电场值和电导率值, Δ z为网格步长。

在节点i+1/2和i+3/2处, 偏导数可以近似为

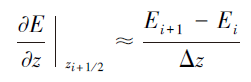
因此, 节点i+1处的二阶偏导数可以近似为

$\begin{matrix} \begin{matrix} \frac{\partial^{2} E}{\partial z^{2}} |_{z_{i + 1}} & \approx (\frac{\partial E}{\partial z} |_{z_{i + 3 / 2}} - \frac{\partial E}{\partial z} |_{z_{i + 1 / 2}}) \\ = \frac{1}{Δz} (\frac{E_{i + 2} - E_{i + 1}}{Δz} - \frac{E_{i + 1} - E_{i}}{Δz}) \\ = \frac{1}{Δ z^{2}} (E_{i + 2} - 2 E_{i + 1} + E_{i}) 。 (2) \end{matrix} \end{matrix}$

根据电磁场基本理论和自然边界条件, 地下无限远处的电场衰减为零, 因此下边界条件为E_n=0, 同时取上边界条件为E₁=1, 结合式(1), 可以得到方程组:

$\begin{matrix} |\begin{matrix} 1 & 0 & 0 & 0 & \dots & 0 \\ \frac{1}{Δ z^{2}} & iωμ σ_{2} - \frac{2}{Δ z^{2}} & \frac{1}{Δ z^{2}} & 0 & \dots & 0 \\ 0 & \frac{1}{Δ z^{2}} & iωμ σ_{3} - \frac{2}{Δ z^{2}} & \frac{1}{Δ z^{2}} & \dots & 0 \\ ⋮ & ⋱ & ⋱ & ⋱ & ⋱ & ⋮ \\ 0 & \dots & 0 & \frac{1}{Δ z^{2}} & iωμ σ_{n - 1} - \frac{2}{Δ z^{2}} & \frac{1}{Δ z^{2}} \\ 0 & \dots & 0 & 0 & 0 & 1 \end{matrix}| |\begin{matrix} E_{1} \\ E_{2} \\ E_{3} \\ ⋮ \\ E_{n - 1} \\ E_{n} \end{matrix}| = |\begin{matrix} 1 \\ 0 \\ 0 \\ ⋮ \\ 0 \\ 0 \end{matrix}| (3) \end{matrix}$

解方程组(3), 即可得地下各节点处的电场值。

根据电磁场基本理论, $\begin{matrix} \frac{\partial E_{x}}{\partial z} \end{matrix}$ =iω μ H_y, 即可得到地面近似磁场强度表达式

$\begin{matrix} H_{1}^{*} \approx \frac{1}{iωμ} (\frac{E_{2} - E_{1}}{Δz}) 。 (4) \end{matrix}$

由此即可利用卡尼亚视电阻率公式^[13]:

$\begin{matrix} ρ_{a} = \frac{1}{ωμ} {|\frac{E_{x}}{H_{y}}|}^{2} = \frac{1}{ωμ} {|\frac{E_{y}}{H_{x}}|}^{2} (5) \end{matrix}$

求解视电阻率。

2 正演模型计算

如前言中所述, 在有限差分算法实现过程中, 网格剖分是非常重要的一个步骤。合适的网格步长既能节约计算时间、减少资源浪费, 又能得到满足精度需求的解。而运用在大地电磁测深法当中时, 由于不同频率的电磁波衰减快慢区别很大, 因此衰减为零时的地层厚度差别非常大, 所以不宜选取同一网格参数来进行差分计算。

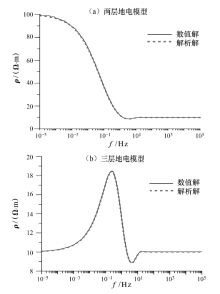
考虑到不同频率的电磁波衰减差别很大, 本文选取了与频率密切相关的趋肤深度δ 作为度量单位, 设计了能够同时适应不同频率电磁波的网格剖分参数:网格步长为 $\begin{matrix} \frac{1}{500} \end{matrix}$ δ , 深度为20δ 。

2.1 层状介质模型

对于一维水平均匀层状介质, 各电磁场分量存在解析解, 即视电阻率也存在解析解^[13]。设计了两层和三层两种层状介质模型(表1), 分别用解析解和有限差分法进行数值求解并对二者结果进行了对比, 结果见图2。

	Figure Option View Download New Window
	图2 层状介质模型数值解与解析解计算结果对比

表1 层状介质模型参数

定义数值解与解析解的视电阻率计算误差为^[14]:

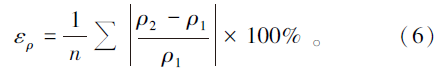
上式中, n为频点数, 本文中取100; ρ ₁、ρ ₂分别为解析解、数值解的视电阻率。

由上式计算的视电阻率误差非常小, 两层介质模型和三层介质模型分别为0.36%和0.21%, 表明了文中所导出的有限差分格式是正确的, 而且网格剖分方法也是合适的, 没有出现低频端剖分不足以致视电阻率曲线上翘的情况^[15]; 同时, 由于采用了同一度量单位, 因此高频端与低频端的计算量是相同的, 并没有为了使低频端数据变好而额外增加高频端的计算量。

2.2 连续介质模型

上面的正演计算假设地电模型是层状的, 但在很多情况下, 连续介质模型也常常被使用^[16]。处理连续介质模型的做法之一是可以把连续介质离散为若干层状介质进行等效。若将连续介质模型假设为层状, 则势必会造成正演结果的不够精确或地电信息的缺失^[17]。因此, 研究电性参数连续变化的一维大地电磁有限差分正演算法是有意义的。同时也可为二维、三维的大地电磁数值模拟正演计算奠定基础。

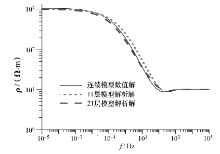
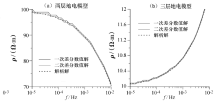
设计了一个准三层地电模型(图3a), 其中第一层和第三层的电阻率为常数, 第二层为电阻率随深度变化而线性增加的连续介质模型。由于这一模型已经不是均匀层状介质模型, 因此无法直接求得其解析解, 只有将电性参数连续变化的第二层近似地分割为多层, 才能得到真实值的解析解, 且分割层数越多, 解析解应该越接近真实值。对此分别设计了11层和21层两种近似层状介质模型(图3b、图3c)。三种模型的正演结果见图4。

	Figure Option View Download New Window
	图3 连续介质模型与近似层状介质模型示意

	Figure Option View Download New Window
	图4 三种模型的解析解正演结果对比

两种近似模型与图3a模型的视电阻率计算误差分别为12.2%和6.9%。可以看出, 近似的均匀层状介质模型与真实的连续介质模型正演结果误差较大, 随着分层数的增加, 误差呈逐渐减小的趋势。

3 网格剖分方法与误差讨论

我们知道, 通过式(5)计算卡尼亚视电阻率时, E_x和H_y分别为地表同一点的电场值和磁场值。而通过有限差分法计算出来的E₁和 $\begin{matrix} H_{1}^{*} \end{matrix}$ , 并不是同一点的场值。如图5所示。

图5中的 $\begin{matrix} H_{1}^{*} \end{matrix}$ , 是通过式(4)所计算得来, 并不等于和E₁在同一点的H₁的值。由电磁场的衰减理论可知, 计算值 $\begin{matrix} H_{1}^{*} \end{matrix}$ 小于真实值H₁, 因此, 计算出的卡尼亚视电阻率比理论值偏大。将图2的低频端单独显示(图6), 即可发现这一细节。

	Figure Option View Download New Window
	图5 E₁和 $\begin{matrix} H_{1}^{*} \end{matrix}$ 、H₁位置示意

	Figure Option View Download New Window
	图6 层状介质模型数值解与解析解低频端计算结果

	Figure Option View Download New Window
	图7 加密的网格剖分示意

	Figure Option View Download New Window
	图8 新型网格剖分下的计算结果对比

由有限差分原理可知, $\begin{matrix} H_{1}^{*} \end{matrix}$ 与H₁的误差大小与网格步长Δ z密切相关。若想减小误差, 必须缩短步长, 而如果全部研究区域都采用短步长, 又会造成内存的巨大开销以及计算时间的成倍增加。因此, 笔者采取了一种新方法(图7):在前文所述的基础上, 通过有限差分算法得到各节点E₁、 E₂、 E₃、…、E_n的值之后, 以E₁为上边界条件, 以E₂为下边界条件, 将之前的第一个网格再进行一次网格剖分, 通过二次差分计算得到一个新的 $\begin{matrix} {\dot{E}}_{2}^{0} \end{matrix}$ , 因此通过式(4)可以得到一个新的 $\begin{matrix} {\dot{H}}_{1}^{*} \end{matrix}$ , 此时的 $\begin{matrix} {\dot{H}}_{1}^{*} \end{matrix}$ 将比 $\begin{matrix} H_{1}^{*} \end{matrix}$ 更接近于真实值H₁, 由此计算得出的卡尼亚视电阻率也将更接近于理论值。采取上述方法改进之后, 效果明显改善。图8给出了计算结果的低频端。

由 $\begin{matrix} {\dot{H}}_{1}^{*} \end{matrix}$ 与 $\begin{matrix} {\dot{H}}_{1} \end{matrix}$ 的计算误差造成的视电阻率误差, 在连续介质模型中也同样不可避免。在采取上述方法改进后, 各模型的视电阻率计算误差对比见表2。

表2 二次差分与一次差分计算值误差对比

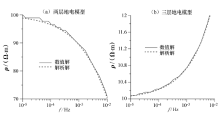
表2显示, 对于层状介质模型, 二次差分的改进效果相对比较明显, 而对于连续介质模型, 改进效果不明显。这表明主要误差来源已经不是H₁的计算不准确, 而是近似的层状介质模型与真实的连续介质模型之间的模型差异。

通过解释网格剖分方法造成误差的原因以及相应解决办法的讨论, 发现误差的大小与网格步长的大小呈正相关; 虽然在初期, 网格步长的减小会使误差急剧减小, 但在达到了足够的计算精度之后, 这种改观已不再明显。因此, 在满足精度要求之后, 没有必要牺牲资源与时间无限制地减小网格步长。

4 结论

(1)提出了一种新的有限差分网格剖分方法, 通过自动变步长适应不同频率的电磁波, 使同一套网格剖分参数可以运用于不同的频段, 既不会使低频端出现欠采样, 也不会使高频端出现过采样。分别通过对层状介质模型、连续介质模型的一维正演计算, 验证了本算法的正确性以及改进网格剖分方法的合理性。分析表明了有限差分算法的正演结果可以真实地反映地下介质的地电特性, 是大地电磁测深正演计算中一种简单、高效的数值模拟方法。

(2)指出了有限差分算法结果的误差大小与网格步长大小密切相关。减小网格步长可以适当提高有限差分数值解的精确度, 但随着误差的逐渐减小, 精确度的提高不再明显, 资源与时间的消耗将大幅增加。因此, 无限制的减小网格步长是没有必要的。

(3)为了兼顾误差大小与网格步长的关系, 采用了一种将一次网格剖分进行二次差分计算的方法得到新的结果, 使计算结果明显得到了改善。而且不同的频点计算量完全相同, 在达到最佳精度的同时不会额外增加工作量。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005. [本文引用:1]
[2]	葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 西安: 西安电子科技大学出版社, 2011. [本文引用:1]
[3]	Anders F Jepsen. Numerical modelling in resistivity prospecting[M]. University of California, 1969. [本文引用:1]
[4]	Mufti I R. Finite-difference resistivity modelling for arbitrary shaped two-dimensional structures[J]. Geophysics, 1976, 41(1): 62-78. [本文引用:1]
[5]	周熙襄, 钟本善, 江玉乐. 点源二维电阻率法有限差分法正演计算[J]. 物探化探计算技术, 1983, 5(2): 1-9. [本文引用:1]
[6]	罗延钟, 万乐. 二维地形不平条件下均匀外电场的有限差分模拟[J]. 物探化探计算技术, 1984, 6(4): 15-16. [本文引用:1]
[7]	周熙襄, 钟本善, 江玉乐, 等. 电法勘探数值模拟技术[M]. 成都: 四川科学技术出版社, 1986. [本文引用:1]
[8]	高本庆, 刘波. 电磁场时域数值技术新进展[J]. 北京理工大学学报, 2002, 22(4): 401-406. [本文引用:1]
[9]	田培培, 冯雪, 关珊珊, 等. 时域航空中心回线源三维异常体的电磁响应探测分辨率[J]. 物探与化探, 2013, 37(3): 538-542. [本文引用:1]
[10]	李鸿军, 黎冬林, 化得钧, 等. 探地雷达在检测预应力梁钢绞线孔注浆效果的应用[J]. 物探与化探, 2013, 37(4): 696-700. [本文引用:1]
[11]	李胜军, 孙成禹, 倪长宽, 等. 声波方程有限差分数值模拟的变网格步长算法[J]. 工程地球物理学报, 2007, 4(3): 207-212. [本文引用:1]
[12]	柳建新, 童孝忠, 郭荣文, 等. 大地电磁测深法勘探——资料处理、反演与解释[M]. 北京: 科学出版社, 2012. [本文引用:1]
[13]	陈乐寿, 王光锷. 大地电磁测深法[M]. 北京: 地质出版社, 1990. [本文引用:2]
[14]	李予国, 徐世浙, 刘斌, 等. 电导率分块连续变化的二维MT有限元模拟(Ⅱ)[J]. 高校地质学报, 1996, 2(4): 448-452. [本文引用:1]
[15]	王涛, 柳建新, 童孝忠, 等. 有限单元法与有限差分法在MT一维正演模拟中的对比分析[J]. 物探化探计算技术, 2013, 35(5): 538-543. [本文引用:1]
[16]	徐世浙, 于涛, 李予国, 等. 电导率分块连续变化的二维MT有限元模拟(Ⅰ)[J]. 高校地质学报, 1995, 1(2): 65-73. [本文引用:1]
[17]	南东辰, 强建科. 大地电磁连续介质反演在庐枞矿集区的应用[J]. 工程地球物理学报, 2012, 9(3): 273-278. [本文引用:1]

2005

0.0

... 因此,研究大地对电磁场的频率响应,可以获得地下不同深度介质电阻率的信息^[1] ...

2011

0.0

... 三种方法各有其优缺点,而有限差分法作为一种经典的数值模拟方法,依靠其相对简单的理论基础及简便的计算过程,在地球物理工作中应用非常广泛^[2] ...

1969

0.0

... 早在70年代初期,Jepsen就对有限差分法电阻率正演数值模拟进行了详细论述^[3],Mufti采用非均匀网格剖分方式达成了以较少节点获得较高精度的目的^[4] ...

1976

0.0

1983

0.0

1984

0.0

1986

0.0

2002

0.0

2013

0.0

2013

0.0

2007

0.0

... 传统的有限差分法网格剖分方式,网格步长都是固定不变的,但这种算法在某些情况下缺乏足够的稳定性^[11] ...

2012

0.0

... 1 有限差分格式推导根据大地电磁测深理论,一维介质中电磁场满足的微分方程为^[12]: ...

1990

0.0

... 由此即可利用卡尼亚视电阻率公式^[13]: ...

... 1 层状介质模型对于一维水平均匀层状介质,各电磁场分量存在解析解,即视电阻率也存在解析解^[13] ...

1996

0.0

... 定义数值解与解析解的视电阻率计算误差为^[14]: ...

2013

0.0

... 21%,表明了文中所导出的有限差分格式是正确的,而且网格剖分方法也是合适的,没有出现低频端剖分不足以致视电阻率曲线上翘的情况^[15] ...

1995

0.0

... 2 连续介质模型上面的正演计算假设地电模型是层状的,但在很多情况下,连续介质模型也常常被使用^[16] ...

2012

0.0

... 若将连续介质模型假设为层状,则势必会造成正演结果的不够精确或地电信息的缺失^[17] ...