TEM中心回线电动势求解全区视电阻率的实用特性

引用本文

蒋邦远. TEM中心回线电动势求解全区视电阻率的实用特性[J]. 物探与化探, 2015,39(3): 530-536.
JIANG Bang-Yuan. Characteristics of applying TEM in-loop configuration induced electromagnetic force formula to the calculation of apparent resistivety[J]. Geophysical and Geochemical Exploration, 2015,39(3): 530-536.
Doi:10.11720/wtyht.2015.3.16 复制到剪切板

Permissions

《物探与化探》编辑部

TEM中心回线电动势求解全区视电阻率的实用特性

蒋邦远

中国地质科学院地球物理地球化学勘查研究所,河北廊坊 065000

作者简介: 蒋邦远(1931-),男,教授级高工,享受国务院政府特殊津贴,1952年南京大学物理系毕业,长期从事电磁法研究。

收稿日期: 2014-05-28

摘要

自中心回线全区电动势响应推导得出后,发表了很多用它求解全区视电阻率特性的文章,总结的特点为:唯一解、双解及无解。它是纯数学理论结果,正确无误,然而并不全面。笔者认为层状大地实测数据求全区视电阻率特征的要点在于曲线的连续性。笔者根据模型研究认为层状大地的曲线都是不连续的,因为无唯一解,在转换点两侧的左右支不是无解就是偏解。因为实测层状大地的数据是非连续采样读取,极少可能正在转换点上,所得响应值大于理论值则无法求得视电阻率(无解),若低于理论值虽可求得视电阻率值,但其值并不正确,笔者命名此特征为“偏解”。“偏解”特征为以往所忽略,为使全区视电阻率曲线连续,采用归一法求全区视电阻率是一个合适的方法。

关键词: TEM; 中心回线; 全区视电阻率; 电动势; 模型计算; 发射回线边长; 阶跃波激发

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2015)03-0530-07

Characteristics of applying TEM in-loop configuration induced electromagnetic force formula to the calculation of apparent resistivety

JIANG Bang-Yuan

Institute of Geophysical and Geochemical Exploration, CAGS, Langfang 065000, China

Abstract

Since the derivation of the in-loop full-zone voltage response formula, many papers have dealt with utilizing it to work out the solution for full-zone apparent resistivity, and the conclusions have three points: unique valued, dual-valued and undefined valued. The conclusions are based on mathematical theoretical analysis. They are of course correct, but not perfect. The main characteristic of the full-zone apparent resistivity curve of observed data is continuous or discontinuous. Based on model study, the author concluded that the main characteristics of an observed data on he layered earth are as follows: the full-zone apparent resistivity curves are all discontinuous, and there are three factors, i.e., no unique value exists because measurements are discontinuous, and therefore sampling time is rarely just at the transition point; undefined value exists because observed value is greater than homogeneous half-spaces; wrongly defined value exists when the observed response is lower than homogeneous half-space's. The last term is named by the author firstly. The normalizing processing is the only method to get the continuity of the full-zone apparent resistivity.

Keyword: TEM; central loop line; whole area resistivity; electrodynamic force; model calcuation; side length of emission loop linestep wave excitation

Show Figures

根据文献[1]记载, 早在1951年, j.R.Wait就推导出中心回线全区感应电动势表达式, 随着瞬变场仪器取样延时日益提早(达到微秒级)以及个人计算机的普及, 在20世纪80年代, 该公式在国内外得到广为应用, 至今已不可或缺。国内发表了不少介绍此公式的文章, 极大地提高了成果的解释水平, 取得好的地质效果。然而凡事皆一分为二, 该公式较之近带视电阻率有很大优点, 但从实用效果来说称之为“ 全区” 尚嫌不足。不知从何时起, 不少文章在叙述利用该公式求解视电阻率之特性时趋于一致, 即:单解、无解和双解, 并强调判断双解之孰为正确极为困难。笔者认为, 就纯数学分析而言, 解的三种情况当然存在, 但并不全面, 双解之判别也并不困难, 更为重要的是全区视电阻率的这些特点如何利用与避免鲜见介绍。从实用观点看, 这些恰是某种视电阻率计算方法优势的检验标准。笔者以模型计算结果为依据对此类问题加以分析。

1 全区视电阻率公式及其特性

1.1 原公式

已有的均匀半空间、阶跃波激发的中心回线电动势响应公式为^{[1, 2]}

$\begin{matrix} ε = \frac{mI}{σ a^{3}} [3 \erf (θa) - \frac{2}{\sqrt[]{π}} θa (3 + 2 θ^{2} a^{2}) e^{- θ^{2} a^{2}}] (1) \end{matrix}$

式中:m— 接收磁矩, a— 发射回线半径, θ =(μ ₀σ /4t)¹^/², σ — 均匀半空间电导率, μ ₀— 自由空间磁导率。

1.2 改写公式

野外工作所用发射回线大多为方形, 延时多为毫秒级, 响应多为毫伏级, 故将式(1)改写为

$\begin{matrix} \begin{matrix} ε = \frac{3 π^{\frac{3}{2}} S_{R} Iρ}{L^{3}} \{\erf (u) - [1 + \frac{2}{3} u^{2}] \frac{2}{\sqrt[]{π}} u e^{- μ^{2}}\}, (2) \\ u = \frac{L}{100} \frac{1}{\sqrt[]{ρt}}, (3) \\ ρ = {(\frac{L}{100})}^{2} / (t u^{2}), (4) \end{matrix} \end{matrix}$

式中:erf(u)— 误差函数; L— 方形发射回线边长(单位m); S_R— 接收线圈等效面积(单位m²); I— 发射电流(单位A); ρ — 均匀半空间电阻率(单位Ω · m); t— 采样延时(单位ms); μ ₀=4π × 10^-7 H/m, 已代入公式中, 故无显示。

将式(4)代入式(2), 整理简化得

$\begin{matrix} \begin{matrix} ε = \frac{3 π^{\frac{3}{2}} S_{R} I}{10 Lt} \cdot \frac{f (u)}{u^{2}}, (5) \\ f (u) = \{\erf (u) - [1 + \frac{2}{3} u^{2}] \frac{2}{\sqrt[]{π}} u^{2} e^{- u^{2}}\} 。 (6) \end{matrix} \end{matrix}$

将式(5)改写为ε 、t两变数之函数F(u):

$\begin{matrix} F (u) = \frac{f (u)}{u^{2}} = \frac{10 L}{3 π^{\frac{2}{3}} S_{R} I} \cdot εt 。 (7) \end{matrix}$

式(5)、式(7)中, ε 的单位为mV。

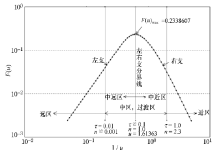
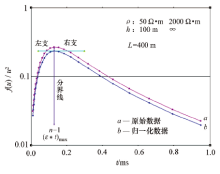
F(u)在一些文章中被称为“ 归一化感应电动势” , 从量纲概念考量, 在本文中称之为“ F(u)函数” 。F(u)函数与1/u的关系曲线示于图1, 此曲线之形状有文章称之为“ 钟形” , 其实更像频率谐振曲线, 曲线随1/u之增长(对于均匀大地也就是随取样延时的增长)逐步上升, 达到极大值F(u)_max后又逐步下降, 极大点的幅值F(u)_max=0.233 896 07, 对应的参数u=1.613 63, 以两者连线为界, 一边称左支, 一边称为右支。根据有关指南^[3], 曲线标出众所周知的远、中、近三区(带), 为叙述方便, 笔者又提出中远带与中近带的分区名词, 从实用考虑, 在特征点处还标出综合参数τ 和延时t的幂指数n。

	Figure Option View Download New Window
	图1 均匀大地F(u)函数与变数u之关系曲线

图1中的正演曲线显示出所有均匀大地的共同特征。设 F(u)为理论数据, f(u)/u²为实测计算值, 以图1曲线很易判断有下述情况:当[f(u)/u²]_max=F(u)_max时有唯一单解, f(u)/ $\begin{matrix} u_{\max}^{2} \end{matrix}$ > F(u)时无解, f(u)/ $\begin{matrix} u_{\max}^{2} \end{matrix}$ < F(u)时有双解。然而, 求解视电阻率的特性尚不止此。

2 全区视电阻率ρ _f的试算

2.1 区带的划分

为确定双解中的正确解, 在计算视电阻率之前, 首先确定左、右支分界线对应的延时是最理想的方法。因为式(7)不是解析式, 数据又是非连续观测得到, 故以确定延时t的幂值n为必要条件:n= $\begin{matrix} \frac{\ln (ε_{i} / ε_{i + 1})}{\ln (t_{i + 1} / t_{i})} \end{matrix}$ , (ε t)_max为充分条件。因为响应为非连续观测所得, 故按实测值求得n=1几乎不可能, 需利用n=1附近的ε 和t插值求得, 而后利用对应n=1的t和ε 值求其乘积, 当作极大值(ε t)_max, 由此区分出左、右两支, 双解分辨问题自然解决。

2.2 ρ _f的计算

采用两种方法求解全区视电阻率。

一种为改良的逐次逼近法, 在式(6)、式(7)中应用。首先, 计算均匀大地F(u) — u的数据表, 存入数据库; 由式(7)求得实测数据; 通过程序数据库查得相应u值, 代入式(4)求得ρ _f。

另一种为归一(化)法。此法有两类, 一类是将式(7)的右项除以K₁(可称之为归一系数), 使[f(u)/u²]_max=F(u)_max=0.233 860 7; F(u)对应既定之u, 将u代入式(4)并乘以K₁得ρ _f; 苏朱刘、胡文宝介绍的方法即属此类^[4]。笔者所用归一法, 是以前述区分区带的(ε t)_max来归一各延时的ε t乘积, 即K₂=ε t/(ε t)_max。可见, 在n=1, 即理论之F(u)_max处, K₂=1, 而不是 0.233 860 7, 但对应的u值相同, 求ρ _f仍用式(4)而不需乘K₂。

两种归一法得到的ρ _f曲线基本一致, 也各有特点。

3 模型计算

3.1 均匀半空间

现有仪器采用的延时比值(t_i+₁/t_i)为1.2~1.3, 为了更好地说明问题, 此计算采用比值为1.1。

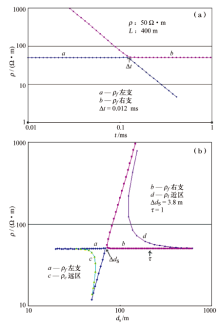
图2a为显示均匀大地ρ _f特征的常用图件。笔者最早见之于spies的文章^[1], 特征与本文相同。图2a中两曲线在[f(u)/u²]_max极值点附近右支ρ _f> 50 Ω · m并愈来愈大, 左支ρ _f< 50 Ω · m并愈来愈小, 即左、右支曲线在极值点并不相连, 而是间断。spies对类似特点未加描述, 也未指出左、右支间断的存在。

图2b为ρ _f — d_s曲线, 为本文第一次采用。d_s为视深度, 其计算式为:d_s=28.08 $\begin{matrix} \sqrt[]{ρ_{f} t} \end{matrix}$ 。图2b更明显地显示出均匀大地ρ _f的特性:ρ _f=50 Ω · m的水平曲线部分为符合定义的左、右支, 而在临近[f(u)/u²]_max处, 按左、右支计算的曲线突然转变方向, 与定义曲线成折线, 左、右支折线部分在模数相等的双对数坐标上为一条直线上, 并与x轴成75° 。这种特征, 笔者命为“ 折返” 。两折返的起点明显不相互连接, 折返现象又是一种分辨左、右支的方法。

	Figure Option View Download New Window
	图2 均匀半空间的ρ _f— t(a)及ρ _f— d_s(b)曲线

由相似准则可知, 此计算个案等同于无数个模型的计算。均匀半空间中电阻率曲线还有间断, 可以推断在层状大地上, 以t_i+₁/t_i> 1.1的不连续观测, 恰恰能取得极大值点的数据的可能性极小。换言之, 不存在[f(u)/u²]_max=F(u)_max单解, 只有近似解, 此解既使对均匀大地亦须观测密度和精度很高方有可能, 称之为“ 视单解” 。

图2b中还给出由远、近带公式分别计算出的ρ _e和ρ _l曲线作比较, 可见早年常用的ρ _l较之ρ _f右支误差甚大, 此例有约120 m的深度无法测到。

3.2 两层大地

3.2.1 G型(ρ ₁< ρ ₂)大地

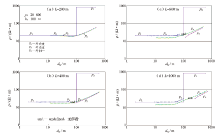
用同一模型, 计算4种发射边长的ρ _f, 结果见图3。图3a的发射边长最短, L=200 m, 由左、右支曲线的特点可知极值约在d_s=30 m处, 处于第一地层中部, 基本无第二层的影响, 故左、右支ρ _f与归一化之ρ _f重合, 在第二地层之边界处d_s=75 m, 有一弱的“ 下凹” , 可谓是标准的G型二层ρ _f曲线。

随着边长L的增长, 左、右支曲线出现无解部分, 曲线间断(不连续), “ 下凹” 消失以及ρ _f左支在无解前的曲线上扬, 明显反映出第二层的影响; 归一化ρ _f则都是连续曲线。无解的原因则是在极大值左、右某段, f(u)/ $\begin{matrix} u_{\max}^{2} \end{matrix}$ > F(u), 无法拟合。

	Figure Option View Download New Window
	图3 G型二层大地不同发射边长的ρ _f— d_s曲线

3.2.2 D型(ρ ₁> ρ ₂)大地

边长L小, 左、右支ρ _f都在第一地层, 未受第二层影响情况下(图4a), 与归一化ρ _f曲线重合, 在二层接触带上曲线“ 上凸” , 为众所熟知的D型曲线。

随着边长增大, 左、右支曲线在采用国外某程序计算中虽未显示无解, 但相互间的距离愈来愈大, 并出现两个未见有文章提及的特征:其一, 上凸幅度以L=400 m条件下为最强, 而后随L再增大而减弱至完全消失; 其二, 左支受第二层的影响随L加大而增强, 同时右支受第一层的影响愈来愈弱, 以致消失(图4d), 相应的归一化曲线随L的增大而与二层大地愈来愈契合。从理论上讲, 此等现象指出边长愈大探测浅层的效果愈好, 然而边长愈大回线的自身暂态愈大, 关断延时愈来愈长, 从而此特点无法利用。

	Figure Option View Download New Window
	图4 D型二层大地不同发射边长的ρ _f— d_s曲线

3.3 间断、无解与偏解

图3、图4中逐次逼近法的ρ _f曲线出现间断(不连续), 其原因是该取样延时的数据无解或偏解。

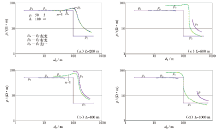
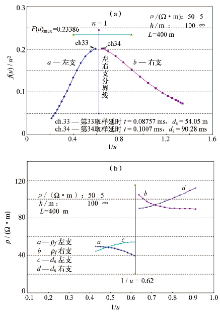
无解有确切的数学诠释, 即已提过的f(u)/u²> F(u)_max。从图5可清晰地看出此例曲线中有4个值大于F(u)_max, 从而ρ _f曲线间断(图3b)。因为无解, 图5的横坐标无法选1/u, 而采用t。

	Figure Option View Download New Window
	图5 G型大地无解的图解

“ 偏解” 的含义是数据有解, 然而偏离了客观实际, 从而导致曲线之间断、不连续。此名词由笔者第一次提出, 可商榷。图6为此名词之图解。图6a中, 左、右支全部有解, 但在分界线两侧, 两相邻延时之比为1.15, 远密于仪器常用的1.25, 但两者对应的视深度差达36.23 m。为进一步说明此现象, 绘制了图6b, 所用步长更密(为1.05), 但分界线两侧相邻延时之Δ ρ _f=50 Ω · m, Δ d_s=36 m。由c、d曲线之特征可知, 如实际步长达1.25, 则间隔更大。

二层大地是各型多层大地的基础, 所以无解和偏解普遍存在, 只要回线边长选择不当, 所有类型之地层的全域视电阻率曲线都会出现不连续。

	Figure Option View Download New Window
	图6 D型大地偏解的图解

3.4 七层大地

一种计算方法是否实用, 以均匀大地试计算是必要条件, 用多层大地并以ρ _f做为高一级的反演方法的初值, 做高一级的反演为充分条件, 本计算即此目的。

七层大地所用一维直接快速反演为实用“ 烟圈” 反演公式^[5]:

$\begin{matrix} \begin{matrix} ρ_{r} = 4 {[\frac{\sqrt[]{ρ_{i + 1} t_{i + 1}^{h}} - \sqrt[]{ρ_{i} t_{i}^{h}}}{t_{i + 1}^{h} - t_{i}^{h}}]}^{2} \sqrt[]{t_{i + 1}^{h} t_{i}^{h}}, (10) \\ t^{h} = t_{r} / \ln (\frac{t_{r} + t}{t}), (11) \end{matrix} \end{matrix}$

其中, t_r— 斜阶跃关断延时, t— 取样延时, 两个参数的单位相同。式(11)即为双曲线关断效应改正公式。

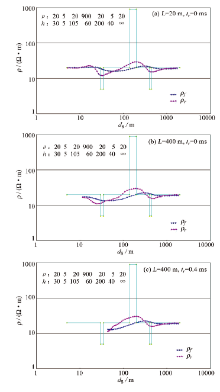
此模型相当于在20 Ω · m的大地中有“ 低” 、“ 高” 、“ 低” 三层其他地层, 以两种发射边长以及阶跃波、斜阶跃波激发, 结果见图7。

图7a为L=20 m短发射边长的结果, 属近带, 故第一低阻层伴有“ 上凸” 畸变。图7b的L=400 m, 其中分带界线约在d_s=80 m处, 即第一低阻层位于远带, 故无“ 上凸” 畸变, 又由于远带的高频成分多, 故低阻异常显示较早。图7c为斜阶跃波激发, 数据经后延改正处理, d_s最浅处已大於第一低阻层的厚度, 故无显示, 这正是长发射回线边长探测浅层不实用的原因。

	Figure Option View Download New Window
	图7 HKH七层大地ρ _r与ρ _f一维反演对比

三种情况中共同之处是“ 烟圈” 反演ρ _r曲线都较全域视电阻率反演ρ _f效果更明显:异常幅度大, 位置与异常体更一致。须指出, 不同边长的异常幅度基本一致, 但纯近带的异常曲线圆滑, 这是因为无中间带左、右支归一问题。然而在实际工作中, 以L=20 m欲探测深度大于200 m的目的物, 发射功率往往不够。

4 全区视电阻率特征归纳

用电动势公式(1)计算视电阻率, 通常所谓单解、双解和无解是一种纯数学分析。将其应用于实际层状大地中, 即使采用阶跃波激发, 存在的主要问题还是曲线的不连续。曲线不连续不仅是由于无解, 还有偏解, 因此是普遍存在的问题, 其解决方法应是恰当地选择发射边长及采用归一法计算。在斜阶跃波激发、后沿改正法不当、接收线圈有暂态的情况下, 逐次逼近法求得的全区视电阻率特征见表1。

表1 全区视电阻率特征统计

序号	地电条件	解的特点	数学条件	曲线特征及说明
1	均匀大地	视单解	[f(u)/u²]_max=F(u)_max	左、右支曲线间断距离不大, 误差可接受
2	层状大地 n=1位于第一层	视单解	[f(u)/u²]_max=F(u)_max	左、右支曲线间断距离不大, 误差可接受
3	G型、K型等大地	无解	[f(u)/u²]_max> F(u)_max	左、右支曲线间断, 不连续
4	D型、H型等大地	偏解	[f(u)/u²]_max< F(u)_max $\begin{matrix} \frac{1}{u_{x}} \end{matrix}$ < $\begin{matrix} \frac{1}{u_{\max}} \end{matrix}$ < $\begin{matrix} \frac{1}{u_{y}} \end{matrix}$ , t_y> t_x	左、右支曲线间断, 不连续
5	层状大地	双解	[f(u)/u²]_max< F(u)_max	计算前未判别区带
6	层状大地	单解	[f(u)/u²]_max< F(u)_max	计算前已判别区带

表1 全区视电阻率特征统计

归一法计算全区视电阻率则适用于全区, 左、右支很易分辨, 唯一要求是数据要包括[f(u)/u²]_max在内。

两种算法的实际应用要点:

Ⅰ :不适用于远带。远带的条件是取样延时很早, 发射边长很大或两者都具备, 而远带的目的物应是浅层、体积小, 故延时虽早但属于远带的时段不够。

Ⅱ :若发射回线边长大, 则关断延时长, 远带大部被后沿改正删去。

Ⅲ :归一法必须包括中带, 如不包括, 则须用逼近法的右支, 但右支靠近中带部分往往有畸变, 出现“ 上凸” 或“ 下凹” 现象。

Ⅳ :中带是过渡带, 往往是无解或偏解, 采用归一法主要是视觉上的改善, 原本应有的信息将会被“ 圆滑” 掉。

Ⅴ :仪器性能无法变动, 地电条件客观存在, 欲取得尽可能满意的地质效果唯一可选择的是发射回线边长。要取得相对合适的边长, 应预先做模拟计算。

5 结论与建议

(1) 式(1)计算电动势属正演, 用于求视电阻率则属反演, 尚有不少问题, 称之为全区视电阻率公式, 易产生误导。

(2) 从应用的条件看, 发射为斜阶跃波, 在关断效应校正法不理想、接收线圈延时较大的条件下, 适用于中— 近区, 达不到全区。

(3) 中带是讯息模糊区, 又不可舍去, 故建议在主要的推断解释图件(拟视电阻率断面图)上绘出(ε t)_max归一值的曲线, 将有助于解释。

(4) 在既定的仪器性能下, 对待客观的探测目的物必须精心设计发射边长。

(5) 探测目的物在浅部和深部都有分布时, 应考虑采用长、短两个回线, 用一个边长的回线往往取不到满意的结果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Spies B R, Eggers D E. The use and misuse of apparent resistivity in electromagnetic methods[J]. Geophysics, 1986, 51(7). [本文引用:2]
[2]	米萨克N 纳比吉安. 勘查地球物理电磁法(第一卷): 理论[M]. 赵经祥, 王艳君, 译. 北京: 地质出版社, 1992. [本文引用:1]
[3]	卡麦涅茨基 ф M. 金属物探过渡过程法应用指南[M]. 李立, 蔡刚民, 译. 北京: 地质出版社, 1980. [本文引用:1]
[4]	苏朱刘, 胡文宝. 中心回线方式瞬变电磁测探虚拟全区视电阻率和一维反演方法[J]. 石油物探, 2002, 41(2). [本文引用:1]
[5]	蒋邦远. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 1998. [本文引用:1]
[6]	朴化荣. 电磁测深法原理[M]. 北京: 地质出版社, 1990. [本文引用:1]
[7]	杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社, 1997. [本文引用:1]