作者简介: 李金丽(1989-),女,汉族,内蒙古赤峰人,现为中国石油大学(华东)在读研究生,主要从事地震波衰减补偿和偏移成像方面的工作。
地震波在地下介质中传播时,由于地下介质的吸收衰减作用,地震波的部分弹性能量不可逆转的转化为热能而发生耗散,使得地震波的能量发生衰减,相位产生畸变,降低了地震资料的分辨率和信噪比。为了实现对地震波的吸收衰减进行补偿,国内外许多学者在这方面做了大量的研究工作。笔者简单介绍了地震波的衰减机制和影响地震波衰减的主要因素,重点概括了各种地震波衰减补偿的研究方法,如反 Q滤波方法、时频分析方法和反 Q偏移方法,分析了各种补偿方法的优缺点。最后用黏声波逆时偏移方法对地震波衰减进行了补偿,并预测了地震波衰减补偿研究的发展趋势。
The energy in seismic waves will be absorbed when the waves travel in the earth,because the medium in the earth is viscoelastic.There are many kinds of energy absorption,such as geometric spreading,intrinsic attenuation, transmission losses,and energy conversion.Such energy absorptions will decrease the signal-to-noise ratio and the resolution of seismic data.In order to realize the energy compensation,many scholars both in China and abroad have tried their best to do a lot of work. In this paper,the seismic attenuation mechanism and the main factors affecting the seismic wave absorption were reviewed.Several kinds of methods of energy compensation for seismic absorption attenuation including inverse Q filtering ,time-frequency analysis and inverse Q migration were emphasized.An analysis shows that these methods have their own advantages and disadvantages.The authors implement the viscoacoustic wave equation for the forward and backward wave propagation to correct the attenuation effects in reverse time migration.A numerical test demonstrates that the attenuation effects in reverse time migration can be properly compensated and the attenuation compensation can enhance the high-wavenumber components in complex geological structures.Finally,the development trend of seismic wave energy compensation is forecasted.
随着对地下介质研究的不断深入, 人们逐渐发现地下介质并非是完全弹性介质, 即使对透射损失、几何扩散等因素引起的衰减补偿后, 地震剖面上中、深层的能量仍要弱于浅层。这表明波在传播的过程中发生了能量的耗损。地震波衰减导致地震剖面上来自深层的能量变弱, 子波发生畸变, 信噪比变低。由于高频比低频衰减得快, 所以使得地震波的主频逐渐变小[1, 2]。目前发展了很多种地震波吸收衰减理论, 而针对不同衰减理论又有不同的补偿方法。文中简单介绍了地震波的吸收衰减理论, 重点论述了反Q滤波、时频分析和反Q偏移等各种地震波衰减补偿方法, 分析了他们的优缺点。最后用黏介质逆时偏移方法对地震波进行衰减补偿, 并在此基础上预测了地震波吸收衰减补偿的发展趋势。
随着地震波理论的不断发展, 国内外学者提出了大量的地震波衰减解释理论[3, 4, 5, 6, 7, 8], 大体上分为以下三类: 一是假设地下介质是非均匀介质, 大地吸收衰减特性用散射理论来解释; 二是假设地下介质是粘弹性介质, 利用Maxwell, Kelvin-Voight, SLS等模型来研究地震波能量的衰减; 三是假设地下介质是双相介质, 主要包括喷射流动理论和BOIT理论。
1.1.1 散射理论
散射是指波在非均匀介质中传播时, 由于介质的非均匀性而致使部分波向多方面改变方向的现象。Chernov针对地震波的散射问题, 运用标量波的传播理论加以解决, 他的这一创造性研究, 开辟了地震波散射理论的新天地。此后, Aki、Chouet、Sato等分别运用Chernov提出的理论来模拟地震波尾波的生成。Seifert等人通过实验验证了, 当未固结的岩石孔隙被流体胶结充填时, 地震波通过该孔隙将发生能量衰减, 究其原因是由散射造成的。Hudson J A和Knopoff[9]通过研究发现, 地震波在经过含有孔隙的介质时能量将发生衰减, 研究发现产生衰减的因素主要有两个:其一是孔隙中的填充物与流体相互耦合的粘滞性造成了能量的耗损; 其二是由于能量的耗散, 改变了原波的传播方向, 将有效地震波转换成了噪声或者尾波。尹军杰等[10]通过对地震波散射理论的研究, 详细地论述了前人在散射波数值模拟和应用方面的不足, 并针对不足提出了一些改进策略。
1.1.2 BISQ理论和喷射流动理论
影响地震反射特征的主要因素是介质的密度和速度。当孔隙中含有流体时, 介质变为双相介质或多相介质, 关于双相介质, 从1982年已经出现了近20种理论。最早的应为Voigt-Reuss模型(1928-1929), 而早期最实用的则是Gassmann方程(1951)。Murphy等[11]验证了致使沉积物中纵横波发生速度频散和能量衰减的主要原因是沉积物的喷流机制。而在1956年, Boit利用潮湿土壤的电位特性和声波的吸收特性, 提出了著名的Boit双相介质理论, 在这之后又出现了被广泛使用的维利(Wyllie)时间平均方程。Dvorkin和Nur[12]在前人研究的基础上提出了BISQ模型, 并将实际数据与理论模型进行试算对比, 验证了所提理论的准确性要高于Boit所提出的理论。Parra[13, 14]在Dvorkin和Nur的基础上, 又将此模型运用到了VTI双相介质中。杨顶辉等[15]在各向异性介质中, 基于介质中固相和液相耦合现象, 提出了BISQ方程。
为了直观形象准确的描述地震波的吸收衰减, 国内外学者引入了大量参数来表征地层的吸收衰减[16], 主要有对数衰减量(δ )、吸收系数(α )、衰减系数(β )和品质因子(Q)等。其中这些参数之间有如下关系
其中:A1、A2是波传播的振幅值。
合理有效地估计和补偿地下介质对地震波高频成分的的吸收, 不仅对于提高地震资料的分辨率和信噪比至关重要, 而且还可以提高偏移成像的精度并为后期地震解释技术提供可靠的依据。诸如谱白化方法[20, 21]和反Q滤波法都是早期使用的衰减补偿方法, 后来又有一些学者提出了很多新方法, 如时频分析法和反Q偏移法等。笔者主要对目前发展比较成熟的几种方法进行归纳和总结, 概括这些方法的优缺点及其可行性。至于其他方法, 这里就不再详细论述。
反Q滤波[22-24]方法可以有效地补偿地震波能量的衰减, 是一种高效的吸收补偿方法。它不仅可以补偿高频能量的衰减, 还可以改善地震记录的相位特性, 从而得到高信噪比和高分辨率的地震资料。反Q滤波方法按实现方法不同, 可以分为基于波场延拓的反Q滤波方法、用级数展开作近似的反Q滤波方法[25-28]和其他反Q滤波方法三大类。由于庞大的计算量限制了用级数展开作高频近似的反Q滤波方法在工业上的应用, 所以这里就不再对其进行详细论述。
为了克服用级数展开作近似的反Q滤波方的缺陷, 许多学者又另辟蹊径寻找新方法, 此时基于波场延拓的反Q滤波方法便应运而生, 其中运用快速傅里叶变换的波场延拓反Q滤波方法[29], 具有高速高效的优点, 广泛用于实际生产中的。
Hargreaves[30, 31]提出了与Stolt偏移成像方法相类似的相位移补偿方法, 然后用级联式展开计算, 逐层进行Q值补偿, 运算速度非常快。但是该方法只能补偿地震波在传播过程中的相位畸变, 且无条件稳定, 没有考虑振幅影响, 所以此方法并不能得到真正的振幅信息。究其原因主要是当反Q滤波中包含振幅补偿因子时会产生不稳定, 随机噪声将会被放大, 湮没有用信息。
Wang Yanghua[32]在Hargreaves理论的基础上提出了一种新的反Q滤波方法。这个方法的主要思想是:把地下介质看成是层状介质, 每一层均为常Q层, 逐层进行反Q滤波。反Q滤波通过以下两个过程实现:①波场正向外推。将地表的波场值正向延拓到目的层顶部, 为了控制稳定性, 加入稳定因子; ②将目的层看成是常Q层, 进行反Q滤波。Wang Yanghua分别对只补偿相位和相位与振幅同时补偿的模型进行了试算, 证明了该方法的高效性和稳定性。Wang Yanghua[33, 34]在2008年又提出了一种以地下介质为水平层状介质为前提, Q是时间或深度的函数的反Q滤波方法。为了控制振幅补偿的不稳定性, Wang在其方法中还引入了振幅增益控制因子, 确保了补偿的稳定性。
王文闯等[35]在Carlos[36]的基础上提出了一种联合时间域和频率域的双域反Q滤波补方法。该方法假设地下是层状介质, 逐层进行延拓补偿, 且每一层的输出都看作是下一层的输入。在每一恒Q层内, 利用波场插值和傅里叶反变换方法在频率域内进行精确的相位补偿, 然后进行时频域转化, 在预先设定的增益控制参数的约束下推导得到振幅补偿算子, 结合第一步, 实现稳定高效的振幅补偿。他们将这个方法应用到中国西部沙漠地区的两条2D测线上进行试算和验证, 通过补偿前和补偿后的叠加剖面对比发现, 补偿后的叠加剖面不仅同相轴的连续性得到了显著改善, 而且地震资料的分辨率也得到提高。
张瑾, 刘财等[37]根据前人提出的反Q滤波不稳定问题, 将解决位场不适定问题的正则化方法与反Q滤波方法相结合, 提出了一种新的衰减补偿方法。该方法以声波方程为基础, 运用傅里叶变换得到正反向外推的精确算子, 然后进行深时转化, 代入速度频散公式, 得到补偿公式。为解决振幅补偿过程中存在的高频随机噪声放大问题, 引入正则化滤波算子。通过模型试算发现, 与常规反Q滤波补偿方法相比, 此方法不仅能对地震波能量进行有效的补偿, 同时还具有较强的抗干扰能力。
姚振兴和高星等[38]在2003年, 针对之前学者提出的反Q滤波补偿算法均是在时间域实现的这一情况, 提出了一种在深度域进行补偿的方法。该方法主要是先将时间域的Q滤波算子, 通过变量代换处理, 转换成深度域的表达式, 然后运用迭代算法进行计算, 最后将此方法用于某地区的叠后深度剖面, 经过试算, 证明了地震剖面经过补偿, 不仅达到了提高地震资料分辨率和信噪比的目的, 而且还确保了地震剖面上中、深层地层同相轴的连续性。
Yan和Liu[39]通过对反Q滤波补偿方法进行推广, 得到了沿着地震波传播路径对叠前PP波和PS波进行补偿的反Q滤波方法。Wang Yanghua等提出的反Q滤波方法都是基于零偏移距的地震记录进行补偿, 而合理的补偿应该沿着波的传播路径进行振幅补偿和相位校正。Yan和Liu提出的方法可以合理有效的对地震波进行补偿, 从而提高了地震记录的分辨率和信噪比。
黄飞[40]在Yan和Liu方法的基础上把反Q滤波方法应用到了多波勘探的地震数据中。借鉴叠后反Q滤波传播算子, 推导了叠前反射波和转换波的补偿算子, 优化了沿着反射波和转换波传播路径进行补偿的算法, 为验证方法的准确性, 将该方法运用到多层CSP道集上, 通过模型试算表明, 与Yan和Liu方法相比, 此方法在提高计算效率的同时, 确保了补偿效果稳的定性。
以上反Q滤波方法虽在地下介质的吸收补偿中发挥了巨大的作用, 但是如何将其成功地应用到实际生产中还是一个难题。目前地震波Q补偿方法在实际生产中仍需要解决以下几个技术难题:准确求取Q值、控制补偿过程中的噪声以及评价补偿效果。很多反Q滤波方法在进行高频补偿之前, 需要准确地估计介质的品质因子, 但是实际地震记录很难准确估计介质的品质因子, 尤其是低信噪比地区。还有一些方法在使用时, 假设地震资料中的噪声是白噪的或者没有噪声干扰, 事实上这与实际是不相符的, 实际资料中不仅含有噪声, 而且有时候噪声干扰还比较严重。噪声的存在首先降低了地震资料的信噪比, 其次在振幅补偿过程中被放大, 淹没有效信息。
鉴于反Q滤波补偿方法补偿前需要求取Q值, 而实际地震资料中Q值又难求取, 许多专家和学者又提出了新的补偿方法。其中时频分析方法同时联合时间域和频率域信息, 是分析非平稳信号的有力工具, 它克服了傅里叶变换中时域和频域完全分离的缺陷。
白桦[41]在地震信号时频分析理论的基础上, 提出了一种基于短时傅里叶变换的地层吸收补偿技术。该方法主要通过如下三个过程实现:①短时傅里叶变换补偿方法, 在原始傅里叶变换理论的基础上增加一个窗函数, 来分段分频描述地震信号; ②提取单一频率的吸收因子, 并将每一个频率的吸收因子进行道集加权; ③将加权后的结果进行短时傅立叶逆变换来重构地震记录, 最终实现地震波的衰减补偿。
将该方法应用到国内某海域2D叠后资料, 实际效果表明该方法无需预知Q值, 能适应常Q和变Q情况, 算法简单、灵活, 易于实现。但是同样也存在着窗函数比较固定, 且固定的窗函数决定了变化率唯一性问题。
李鲲鹏[42, 43]针对短时傅里叶变换中所加窗函数的形态比较单一, 不能反应不同时刻地震信号的变化这一问题提出了另一种补偿方法。此方法先将地震信号用小波函数分频, 然后根据地层吸收特点, 提取各个频率的吸收因子, 对小波系数进行倒数加权, 将加权后的系数用于地震记录的重构, 以此来消除地震波的吸收衰减。该方法同样对Q没有严格要求, 具有普遍适用性。实际资料处理效果表明, 该方法不仅可以消除地下介质对地震波的吸收衰减, 还可以提高地震资料的品质。
由于小波变换是一种时间— 尺度分析方法, 尺度和频率之间没有直接联系, 其适用范围受到一定的限制。Braga L L S 和Moraes F S[44]提出了将小波变换和反Q滤波相结合的小波域的反Q滤波方法。该方法为了防止在振幅补偿的过程中, 将噪声放大, 采用了在小波域进行反演的方法。理论与实际数据表明, 该方法不仅可以提高地震资料的垂直分辨率, 而且在Q值估计不准确的时候, 地震资料也能得到很好的补偿。
S变换是集短时傅里叶变换和小波变换于一体的一种时频分析方法。与短时傅里叶变换相比, S变换的窗函数宽度是可变的, 与小波变换相比, S变换可以直接与频率相联系, 基于以上原因使得S变换在地震资料的时频分析中得到了广泛应用。
Stockwell等[45]提出了S变换的表达式, 并利用S变换方法对地震波的衰减进行补偿。与短时傅里叶变换和小波变换等时频方法相比, S变换的时频谱分辨率与频率相关, 具有多尺度多分辨率分析的能力。但是S变换仍然具有缺陷, 其窗函数随着频率变化比较单一, 不能依据需要进行修改, 缺乏灵活性。
针对S变换中窗函数形态单一, 不能用于实际生产这一难题, 很多专家和学者在原有方法的基础上进行了改进, 提出了广义S变换的补偿方法。
Mansinha等[46]将高斯窗函数中的f用f/γ GS替换, 推导可得
当γ GS取值偏小时, 可以改善S变换的分辨率, 但是同时会影响频率域的分辨率, 解决此问题的方法就是选择不对称的窗函数。McFaden等[47]给出了窗函数不对称的广义S变换; Pinnegar等[48]在窗函数为非对称的前提下, 给出了窗函数标准差可调节的广义S变换; 高静怀等[49]将S变换中的变换基函数gf(t)exp(-i2π ft)一起进行考虑, 在原有基础上进行了改进。
张固澜等[50, 51]依据广义S变换提出了改进的广义S变换, 实现了地震波的高频补偿。其主要思想是:假设地下是完全弹性介质, 地层没有衰减, 则来自地下深层的反射波与浅层相比, 除了相位谱相差一线性系数外, 具有相同频率宽度的振幅谱。
地震信号可以看成是不同频率成分组合而成, 而各频率所对应的能量分布规律具有相似性。由于地下是非弹性介质, 存在着对能量的吸收衰减作用, 使得不同频率能量分布不相同, 通过给地层乘以一个时变系数使其能量分布相同, 来实现对地层的吸收补偿。
将该方法用于一实际VSP数据进行衰减补偿, 通过对比补偿前后的剖面图发现, 此方法不仅能进行无损的广义S变换, 而且还能提取时变Q值, 解决了传统方法中Q补偿存在的问题。
孙佳琳[52]在其硕士论文中提出了以Curvelet变换为基础的衰减补偿方法。Curvelet 变换是一种新的多尺度, 多分辨率分析方法。该方法首先用 Curvelet 变换对地震信号进行分频处理, 然后根据 Curvelet 变换特点, 提取各个时间点处的加权因子并用倒数进行加权, 使各频段相应角度信号深浅层能量比相同, 最后重构加权后的数据。利用该方法对地震数据进行补偿处理后, 地震剖面深浅层反射波能量基本相同, 中深层地震资料分辨率有所改善, 高频成分得到恢复, 地震波有效频带变宽。
以上各种时频分析方法在地震波的吸收衰减补偿方面都发挥了巨大的作用, 与反Q滤波方法相比, 时频分析方法无任何假设条件, 无需求取Q值, 是分析非平稳信号有效工具。其中改进的广义S变换, 由于所加高斯窗的窗宽度是频率的函数, 满足了地震波衰减补偿的要求, 所以其补偿效果要优于短时傅里叶变换和小波变换等方法。
目前, 地震波主要的衰减补偿方法有反Q滤波、时频分析和反Q偏移等方法。反Q滤波方法只是对单道地震记录进行衰减补偿, 忽略了传播路径上吸收衰减的影响, 且吸收衰减往往是发生在波传播路径上, 因此不能进行合理的补偿。而反Q偏移[53-54]方法拥有足够精确的传播算子时, 可以对地下介质进行高效的补偿。反Q偏移根据原理的不同, 主要分为基于射线追踪理论、单程波动方程理论和双程波动方程理论三大类。
在以波动方程为理论的偏移成像方法没有出现前, 以射线追踪为理论的偏移成像方法一直占有主导地位, 随着人们对地下介质认识的不断深入, 运用射线理论进行真振幅偏移成像[55, 56]也逐渐得到了专家和学者的青睐。
任浩然和王华忠等[57]基于射线理论提出了一种沿射线路径进行衰减补偿的方法。由于地震波的吸收衰减主要发生在波的传播路径上, 所以此方法首先要准确地确定地震波的传播路径, 然后沿着波的传播路径进行衰减补偿, 最后对利用粘弹性波动方程得到的正演炮记录的垂直分量进行衰减补偿, 通过与没有衰减的正演炮记录对比发现, 补偿后的地震剖面形态更加清晰, 能量得到了加强。虽然此方法实现了地震波吸收衰减补偿, 但是其稳定性还有待商榷。
Xin等[58]和Xie等[59]基于射线追踪理论的偏移方法, 在波的传播过程中根据传播路径和传播时间进行衰减补偿。Maud Cavalca等[60]提出了在复杂介质中基于射线追踪和波场外推理论的Q补偿方法。该方法是分别将Q补偿与Kirchhoff偏移方法和逆时偏移相结合, 达到在偏移成像的过程中对高频进行补偿。
以上方法都是基于射线追踪理论, 这些方法均实现了沿着波的传播路径进行补偿, 具有运算速度快等优点。但是射线理论忽略了波的动力学特征, 只考虑了波的运动学特征。
随着地震波波动理论的发展, 以波动方程[61]为理论的偏移成像方法如雨后春笋般蓬勃发展。而在黏介质中基于单程波方程理论[62, 63, 64, 65, 66]的偏移补偿方法显示了其强大的生命力。
Dai等[67]推导出了纵波方程反Q滤波算法。杨午阳[68]在其博士论文中实现了2D和3D的频率— 空间域粘弹性波动方程保幅偏移算法。Mittet等[69]推导了黏声波有限差分方法, 并将此方法用于衰减补偿。张立彬和王华忠[70]对反Q滤波方法的稳定性进行了讨论, 结合稳定因子法和增益截频法, 详细的论述了偏移过程中出现的不稳定问题。为控制偏移过程中的假频, 提出了新的压制方法。Valenciano等[71]运用单程波动方程对地下粘介质进行补偿。
孙天真等[72]提出了基于粘声介质的反Q滤波叠前深度偏移方法对地震波进行衰减补偿。他们基于现有的衰减补偿方法, 首先运用单程波方程理论, 将地下介质的真实速度用复速度替代, 这里复速度是频率和品质因子的函数, 然后在f-k域推导传播算子。为了提高算子的精度, 将延拓算子进行展开计算。最后对Marmousi模型进行反Q滤波叠前深度偏移, 模型的速度采用李氏经验公式进行求取, 通过与单程波叠前深度偏移对比发现, 该方法能恢复反射界面的中深层能量, 同相轴连续性得到改善, 拓宽了频带, 使得频率信息变得更丰富。
李雪英等[73]提出了黏性介质叠前时间偏移方法。他们假设地层的Q值是常数, 用等效Q值来代替随时间和深度变化的Q值, 克服了反Q滤波中不能处理Q值为非均匀情况的难题。该方法主要有以下三个关键点:①理论公式推导, 推导出了粘性介质中旅行时和振幅的计算公式; ②运用反褶积成像条件进行偏移成像, 在成像过程中引入高频补偿算子保证其稳定性; ③模型试算, 运用二维模型分别进行常规叠前时间偏移和黏性补偿的时间偏移。
通过对比发现, 该方法具有对地下复杂构造进行稳定、高效成像的能力, 能在偏移成像过程进行衰减补偿, 可以准确获得深层界面的反射信息。
前面提到的方法都是基于波在传播路径上运用单程波动方程偏移成像进行补偿的。为了克服单程波补偿的缺陷, 将地震波衰减补偿理论与双程波动方程偏移相结合, 提出了黏介质逆时偏移[74]对地震波进行衰减补偿。
Deng Feng和 McMechan G A等[75]在完全弹性介质逆时偏移理论的基础上提出了黏弹介质真振幅叠前逆时深度偏移方法。该方法对标准线性固体模型, 采用空间八阶, 时间二阶的高阶有限差分法进行数值模拟。在偏移成像过程中, 为了重建各个反射层P波的振幅信息, 根据四种波之间的关系, 运用Zoeppritz方程求解各种波的振幅信息。在优化方程的同时, 将Q补偿算子引入到偏移算子中, 实现地下介质的衰减补偿。利用该方法分别对倾斜地层和盐丘模型进行真振幅逆时偏移成像, 证明了该方法可以高效、稳定地补偿地震波在传播过程中能量(几何扩散、固有衰减、透射损失和能量转化)损失。但是这种方法存在着计算量大和耗费计算机内存的缺点, 如何有效减少计算量, 降低存储仍是需要解决的问题。
李振春和郭振波等[76]将最小二乘算法和逆时偏移相结合提出了黏声介质最小平方逆时偏移。通过将地球物理反演方法与黏介质逆时偏移成像相结合, 不仅克服了反Q滤波补偿存在的不稳定性问题, 而且还提高了振幅补偿的高保真度。该方法主要分为以下四个步骤:①优化方程, 将其转化为线性形式, 并建立黏介质最小二乘逆时偏移目标函数; ②求解目标函数, 得到目标函数的解, 与此同时求解正向外推和反向外推的偏移算子; ③引入动态相位编码技术。将最小二乘逆时偏移的计算量降低到与常规逆时偏移相同, 来克服逆时偏移计算量大和存储量大的缺点; ④模型试算。将此方法应用到简单的平层模型和盐丘模型中。通过测试发现, 此方法可以很好的对地下复杂构造形态进行成像。
Bai Jianyong 等[77]提出了粘声介质的逆时偏移对地下介质振幅衰减和速度频散进行补偿。该方法主要是在时空域采用标准线性固体模型来模拟地震波传播过程中的吸收衰减, 然后利用伪谱法求解粘声波方程。粘声波方程为
其中, r=
式中:P=P(x, t, xs)为t时刻, 炮点位置在xs, 接收点在x处的波场值; f是震源项, H(t)是单位阶跃函数, r是记忆变量, 用来描述黏性介质的损耗机制; 应力松弛时间τ σ 和应变松弛时间τ ε 可以通过品质因子求解
其中:ω 是角频率, 方程(5)中τ 是无单位的量纲。τ =τ ε /τ σ -1, 由于实际地下介质的Q值往往大于20, 故近似有τ ≪1。
方程(4)中如果不考虑震源项影响, 得到频散关系
式中:v0为速度且为常数。经过近似及其整理可以得到|k|和ω 之间的关系:
从而得到了t-x域的频散关系为
上式中, 第二项是伪谱法— 有限差分算子, Δ 是拉普拉斯算子, 此时方程中记忆变量已经被消去, 不含有记忆变量。方程中包含着衰减项和频散项。如果只考虑衰减可以得到下式
式中:“ +” 代表正向传播, “ -” 代表反向传播。
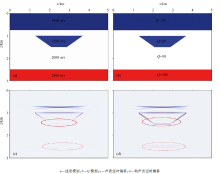
运用此方法对断层模型进行测试, 来检验所提方法的准确性(图1)。速度模型和Q模型分别如图1a和图1b所示, 在模型中梯形区域是低速和低Q区域, 低Q区域代表着强吸收区域, 模型试算采用主频为18 Hz的雷克子波, 每炮共501个接收道, 道间距为8 m。图1c是声波逆时偏移的结果, 图1d是粘声波逆时偏移的结果。通过对比可以知道, 常规声波方程逆时偏移中, 低Q值区域下面的同相轴模糊不清, 地震波吸收比衰减较严重。利用文中所提出的方法进行逆时偏移, 偏移结果证明, 衰减得到了很好补偿, 振幅得到恢复, 梯形低Q区的边界及其下方的水平同相轴(图中椭圆所示)更加清晰, 得到了高分辨率成像剖面。
为了直观地表示粘声波偏移对地震波衰减能量的补偿作用, 分别抽取声波和粘声波逆时偏移之后的某一道集的部分数据, 并画出其振幅曲线图, 如图2所示。通过振幅曲线发现, 粘声波逆时偏移确实在一定程度上可以对地震波的衰减进行补偿, 使振幅得到加强。
在进行反Q偏移成像或者反Q滤波补偿时, 为了研究的方便, 总是假设Q值为常数。实际上Q值并不是常数, 而是变化的, 因此在偏移成像以及反Q滤波补偿时, 需要准确估计Q值大小, 然后再对衰减进行补偿。而实际资料中Q值很难被准确估计, 若估计的Q值远小于真实Q值, 在地震波补偿的过程中, 将造成欠补偿, 致使中深层高频部分的能量不能得到有效的恢复, 深部能量微弱, 最终使得深层地质构造不能准确成像。如果估计的Q值远大于真实Q值, 在地震波补偿的过程中, 将造成过补偿, 使得高频能量被过度补偿, 从而引起补偿算子的不稳定, 噪声被放大, 使得深部的有效信息被高频不稳定能量及噪声所淹没, 最终影响地质构造的成像精度。因此Q值的准确估计与否, 将直接关系到偏移成像的精度。随着地震勘探技术的不断发展, Q值估计方法也得到了迅速的发展, 关于如何准确提取Q值, 这里就不再详细论述。
由于波动方程叠前深度偏移具有对地下复杂构造进行成像的能力, 所以其现在变成了主流的偏移成像方法之一, 该方法不仅对剧烈变化的速度场具有很好的适应性, 而且还能对复杂构造和陡倾角进行成像。但它不能对地下介质进行准确的补偿, 只有将地层的非弹性吸收效应考虑到偏移成像中, 才能得到地下复杂构造的准确形态。同样, 随着各种偏移成像技术的发展, 反Q偏移技术也得到了飞速的发展, 已经从单程波方程发展到了双程波方程。但是如何应用到生产实际还是一个难题。
随着人们对油气需求量的不断增长, 深层油气藏勘探已成为当今勘探研究的主要对象, 但是由于地下介质是非均匀的, 地震波在地下传播的过程中要发生能量的衰减和波形的畸变, 只有合理有效实现对地震波衰减的补偿, 才能得到地下介质的深层信息和构造特征, 以及获得高信噪比和高分辨率的地震剖面。目前发展比较成熟的地震波衰减补偿方法主要有谱分解、反Q滤波、时频分析和反Q偏移等, 并且每个方法都有其各自的优缺点。
反Q滤波补偿理论经过几十年漫长的演化, 已经由不稳定发展到稳定, 由只补偿相位到既补偿相位又补偿振幅, 逐步形成了完整的理论体系。由于反Q滤波需要求取Q值, 故使得补偿质量的优劣将与Q值的准性息息相关, 但是一般情况下, 地下结构形态比较复杂, Q值很难准确求取, 从而限制了反Q滤波补偿方法在实际生产中的广泛应用。时频分析方法是处理非平稳信号的有效手段, 可同时兼顾信号的时间域和频率域信息, 无需预知Q值, 在地震波衰减补偿方面发挥了显著的优势。反Q偏移方法是沿着波的传播路径对地震波进行衰减补偿, 确保深层的能量得到有效恢复, 获得深层复杂构造的地震剖面信息。
笔者仅对粘声波逆时偏移原理进行了初步验证, 如何将这一方法应用到实际生产中还有待于进一步研究。随着多波多分量勘探技术的发展, 如何实现联合P波和SV波地震波衰减能量补偿也将是今后研究的一个热点。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|
| [62] |
|
| [63] |
|
| [64] |
|
| [65] |
|
| [66] |
|
| [67] |
|
| [68] |
|
| [69] |
|
| [70] |
|
| [71] |
|
| [72] |
|
| [73] |
|
| [74] |
|
| [75] |
|
| [76] |
|
| [77] |
|