作者简介: 赵博(1985-),男,博士,主要从事矿床地球化学、区域地球化学等方面的研究工作。E-mail: xqqelove@163.com
以浙西北地区1:20万Cu水系沉积物测量为例,通过含量排列法对由分形求和法所圈定的地球化学异常区进行了内部结构分析,认为无标度区掩盖了异常场的内部结构。借鉴前人提出的含量排列法,将异常区数据从小到大按顺序等间距自然排列,并用三段直线( L1、 L2、 L3)进行拟合, L1为一级异常, L2、 L3被归入二级异常。结果发现,一级弱异常基本不含矿,但仍有个别矿点落入该区;二级异常近似代表了矿致异常,与区域断裂、岩浆活动中心在空间上具有更显著的相关性,从中强调了岩浆源区、构造背景转换和断裂交汇的控矿意义,由此圈定出了一些重点异常作为下一步成矿预测工作的首选靶区。
With 1:200 000 stream sediment survey of copper in northwestern Zhejiang Province as an example, the authors used the content arrangement method to study the internal structural features of Cu geochemical anomalies delineated by the Fractal Summation Method in this area. It is the stability of fractal non-scale section that masks the internal spatial structure of the anomalous field, and the ignored fact therein is that such an internal structure can be manifested by a natural revelation or content arrangement (of copper from small to large content) of the original anomalous sample data itself, rather than an effort to overcome the stability of non-scale sections. Three lines of L1, L2, and L3 are used to fit the hierarchical evolution trends, namely the internal structure, of anomalous data, and therein, L1 specifies the primary anomaly, and L2+L3 specify the advanced anomaly. Studies show that the primary anomaly (L1) may correspond in general to a weak mineralization and essentially barren area, although it does contain some weak mineralization or several hidden ore spots; the secondary one (L2+L3) can be approximately or equally considered as the mineralized anomalous area, between which and the regional tectonomagmatic activity there is a further significant spatial correlation; some new undiscovered copper prospecting target was discovered at last on the basis of the study of the ore-controlling significance of magmatic source, tectonic transformation, and convergence of faults in this area.
从具有随机性的地球化学数据中了解元素的分布特征, 是揭示元素矿化富集及空间变化规律的重要途径之一[1]。Allegre和Lewin[2]针对地球化学场元素的分布形式进行了详细的分析, 将其划分为两大类和四大亚类:正态和多模式分布、分形和多重分形分布, 又对其形成机制进行了详细的研究, 指出正态和多模式分布对应于混合作用占主导地位的地球化学过程, 分形和多重分形分布则对应于分异占主导地位的地球化学过程; Cheng[3]则认为, 地球化学元素的正常值往往服从统计学中的大数定量, 即满足正态分布或对数正态分布, 用于描述多维分形围绕均值周围的局部特征; 赵鹏大等[4]补充到, 关于呈正态分布的地质变量的成因, 一般认为是由许多微小的随机因素综合作用的结果, 它们之间势均力敌, 没有一个因素是突出显著的。然而, 异常值会服从分形— 多重分形分布, 事实上, 地质— 地球化学过程既非完全无序, 又非完全有序[5], 而是介于二者之间, 即处于分形自组织态; 地质现象的复杂性和自组织程度, 可用分维数D和无标度区宽度[6](如异常区面积等)进行定量刻画。
本次研究和思考主要基于MATLAB平台, 由算法相对简单的分形求和模型(fractal summation model)入手, 以含量排列法(content arrangement method)为主要分析手段, 对浙西北地区1:20万Cu水系沉积物测量数据进行内部结构分析, 以期为该区下一步找矿工作提供参考。
Shen[7, 8]认为, 分形分布要求大于(等于)某一尺度的数目, 与物体大小之间存在幂函数(power-law relationship)关系, 即具有尺度不变性, 并提出了分形求和模型用以确定地球化学数据分组界限。现简要介绍之。
设分形模型N(r)=Cr-D, r> 0[7],
其中, r表示特征尺度; C> 0, 称为比例常数; D> 0, 称为一般分维数。N(r)=N(≥ r)表示尺度大于(等于)r的数目或和数, 如N(r)可以表示元素品位大于(等于)r时的样品数目或和数。
设某成矿元素的含量值为{xi}, i=1, 2, …, N, 则有
该式旨在针对所有满足xi≥ r的i求和, min(xi)≤ r≤ max(xi), 其中1≤ i≤ N。于是得到数据集{N(ri), ri}, 将这些数值代入分形模型并对等式两边取对数, 则问题化简为一元线性回归方程
用最小二乘法即可求出斜率的估计量, 即分维数D; 而当N(ri)— ri散点大致分布在二段(或二段以上)的直线时, 另可采用分段拟合求得D1、D2(、D3, …), 不同分维数之间的界限点为异常下限T。大量证据[8]表明, 元素含量的分布的确具有某种分形特征, 甚至导致矿石形成的那些物理和化学过程在相当大的尺度范围内是标度不变的, 但这并没有限制其他成矿理论的提出。这样, 通常会产生所谓“ 两种分形” 的概念, 它们有时分别称为“ 构造” 分形和“ 结构” 分形[9]。D1反映的是具有大区域尺度特点的分形, 系统因素起主导作用, 代表由较低含量值(点)控制的背景区或亏损区; D2和(或)D3则体现了较小尺度的特征, 如局部范围的变化以及各种随机因素(如矿化— 蚀变)的影响等。Turcotte等[10]认为, D2主要反映元素的较高浓集分布特征, D1反映较低的背景值, 两者的分离是由于存在元素在矿床中的富集上限所造成的。Arias等[6]指出, D2值越小, 则拟合的直线越平缓, 元素从低含量点到高含量点的变化频率下降得越慢, 元素含量在空间上的丛集程度越高, 意味着存在着较多的高含量点, 有富集成矿的趋势; 反之, D2值越大, 则高含量点分布较少, 意味着主要含量点集中在低含量区, 也就不存在富集成矿的可能[11]。如果没有高效的富集机制D2, 即便是最有利的构造环境、高丰度背景等也只能产出一个面积巨大、低品位的异常, 而不是矿床[12]。分形模型展示了地球化学场的“ 背景— 异常” 二元结构。因此, 较早的文献[7, 13]通常将D1→ D2的第一拐点作为异常下限。但近来研究发现, 这样的异常下限值在很大程度上与背景值相近, 或者就是背景值, 于是出现了异常下限偏低的现象, 甚至异常区大于背景区。大多数研究者已经注意到这一问题, 并已经解决了这一问题[14, 15, 16], 如采用多重分形的第二拐点作为异常下限值[17]等。笔者无意解决异常场“ 是否可以再分” 的问题, 或对已知地球化学异常进行所谓“ 二次圈定” , 而是考虑在稳定的分形无标度区条件下, 如何剖析异常场的内部结构, 因为这涉及到区分矿致异常和非矿致异常等问题, 具有重要的理论和实践意义。
赵博[18]曾对浙西北地区(118° 00' ~119° 00'E, 28° 40'~29° 40'N)Cu1:20万水系沉积物测量的分形数据特征进行了研究, 将总计2 860个样本数据(除图幅东北角个别弃点外, 采样点基本覆盖整个研究区域, 采样间距严格按1:20万区域地球化学勘查规范执行, 采样分布图及其他说明见参考文献[33])全部代入Shen[7]的分形求和模型, 结果如图 1。在图中, D1、D2依次为相应组段(即无标度区)的斜率, 前者代表地球化学背景场分维, 后者代表异常场分维; N1、N2表示相应组段内的样品数目, 样本数共计2 860个; T为两组段的分界点, 可作为异常下限; 取采样步长即ri→ ri+l, l=1代入分形求和模型进行计算, 详细步骤见文献[6]。N1和N2的线性拟合优度分别为0.942和0.917, 表示拟合程度较好。本文附录部分给出了计算模型(分形求和法)的MATLAB源代码。这里, 步长l规定了计算机扫点的密度。l=1时, 2 860个化探样品被全部纳入计算; l=2意味着从第一个样品点起, 每隔一个点纳入计算, 这样只有1 430个点参与统计; 其他以此类推。图2a考察了扫点密度的降低(l增大)对无标度区稳定性的影响。
根据异常下限(T)发现, 仅有45%的样品归入了背景值的范畴, 另外55%的样品被圈定为异常, N1/N2≈ 0.82。韩东煜等[19]认为, 在化探异常比较显著的情况下, 由分形确定的异常下限(T)要高于传统方法(均值± 2倍方差)确定的异常下限, 从而可以减少异常查证的面积, 达到迅速定位靶区的目的。在化探异常不够显著的情况下, 由分形确定的异常下限一般低于传统方法确定的下限值, 进而在客观上增大了异常的面积, 避免漏掉有用的弱异常信息。然而, 这种“ 异常大于背景” 的情形显然使得每一个有地球化学找矿经验的人都感到陌生无比, 因为它不可避免的扩大了异常查证的范围和工作难度, 继而难以有效追踪并发现矿致异常源, 或者难以排除与预测对象无关的干扰信息。Ma等[20]认为, 应注意在双对数坐标图上拟合的含量— 累加样品数量关系, 如果靠近纵坐标的近似水平分布的曲线所代表的含量位于实验室测试的检测限附近, 就应当谨慎处理, 因为这部分数据的可信度较低, 不能简单视为背景分布。但事实上Cu的检测通常使用火焰原子吸收法测定[21], 最低检出限为0.05× 10-6, 这一批样品中Cu的最小含量为2× 10-6, 远远高于最低检出限, 因此不存在检测限问题。由此, 我们将其归因于分形无标度区及分维数的稳定性, 认为这种稳定性掩盖了异常场的内部结构。
尽管李长江等[13]列举了D2表征金属成矿潜力的众多优势, 但这种将矿致异常和非矿致异常(次生富集)糅合在一起并使用D2进行统一描述的做法, 有时并不利于成矿预测。无标度区的稳定性由图2说明。如图2a, 大幅度改变取样步长l, 异常下限(T)的位移并不明显。图2b试着只针对图1中的异常场数据(N2=1 562)再进行一次分形求和计算, 但异常区仅具有单一分形结构, 这很可能意味着无标度区因其稳定性而难以进行二次分解。图2c中, 我们将图1的研究区范围分割为2~4个等面积的子区域, 但除了个别子区的N1/N2比值较高外, 大部分子区异常大于背景的情况并没有得到明显抑制; 另如118° 30'E~119° 00'E和28° 40'N~29° 10'N等子区范围内的N1/N2虽然高达1.17, 但异常下限T仅为19.5, 远远低于Cu的克拉克值, 更不可能成为矿致异常。总之, 具有成矿潜力的异常不等于最终都能成矿, 如许多赋存大量具成矿潜力花岗岩的地区最终成矿的花岗岩仅是其中的一小部分, 因此从潜力到“ 实力” 的过渡有赖于进行异常结构剖析[22, 23, 24, 25], 但这必须借助于其他方法。
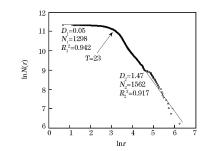 | 图1 浙西北地区1:20万Cu水系沉积物测量N(r) — r双对数图解 [18] |
异常下限的确定, 在矿产勘查和资源预测中占有十分重要的地位。杨大欢等[26, 27]在研究背景和异常关系的基础上, 提出了一种求地球化学异常下限的有效方法, 即含量排列法, 该方法并不要求数据服从正态分布或分形分布, 而是通过对原始数据从小到大进行自然展示求得异常下限。所谓“ 自然展示” , 具体来说, 假定一个化探工作区域(或图幅)同时涵盖了背景区和异常区, 不妨将这些化探数据从小到大(或从大到小)按顺序等间距自然排列, 以排列方向为横坐标, 以元素含量为纵坐标, 则元素含量点的排列可拟合成几段斜率不等的直线段。由于导致背景场与异常场的主要地质— 地球化学控制因素不同, 因此其所形成的元素含量分布图式有所不同, 这样由元素含量顺序排列拟合成的直线, 斜率缓的与背景场对应, 斜率陡的与异常场对应。杨大欢等[27]以广东始兴地区矿产远景调查工作为例, 通过含量排列法确定出该区水系沉积物单个元素的多级异常下限, 证实其较之于传统方法(均值± 2倍方差)更好地反映了研究区的地质背景和实际矿化特征。笔者针对Cu地球化学异常场的内部结构剖析, 在很大程度上借鉴了这一思想, 因为金属在异常场成矿富集的阶段、效率或成因(非矿致、矿致)不同, 由含量排列法拟合的直线斜率及样品数目必不相同。
从背景到异常意味着由缓慢的、长期的“ 量” 的积累到革命的、激变式“ 质” 的飞跃, 但这种飞跃是分阶段或分层次完成的。图3为异常场原始数据从小到大的自然展示。图3a表明Cu在异常场的概率密度分布并不符合正态分布, 这与引言中Cheng[9]的认识相吻合, 但其中明显存在具有高、中、低频率的3个子段, 对比图3b这种趋势更为清晰。于是, 异常场的内部结构由此显明:Cu仅在图 1异常区中含量由小到大变化时, 可以用3段直线进行拟合, 变化速率(斜率):L3> L2> L1, 分布面积(频率):L3< L2< L1, 相应的界限点依次为T2、T3, 这里使用脚标2、3是相对于图1中的T(这里为T1)而言的。从中可划分出:一级异常(即子段L1, 平均含量为28.61× 10-6, 阈值T1=23× 10-6)、二级异常(即子段L2, 平均含量为47.96× 10-6, 阈值T2=35.5× 10-6)、三级异常(即子段L3, 平均含量为176.68× 10-6, 阈值T3=99.5× 10-6), T2/T1=1.54、T3/T2=2.80、T3/T1=4.33。以本区桐村斑岩型Mo矿床为例, 该矿床本身富Mo而相对贫Cu(或伴生少量Cu), 钻孔数据显示Cu的最低含量[18]为49× 10-6左右, 仅略高于T2, 因此不妨将T2作为矿致异常与非矿致异常的界限点。不得不承认, 弱异常也可能成为矿致异常或与隐伏矿体有关的异常[22]。如研究[3, 4]表明, Cu 与 Ni的含量比值, 可以辨认与基性岩有关的非矿异常, 因为基性岩中 Cu-Ni 含量比值较低, 而铜矿引起的铜异常Cu-Ni含量比值较高; 研究冷提取金属(Cu)与金属全量的比值(相态分析), 可以分辨水成异常和碎屑异常, 从而可以判断覆盖层下矿体的可能位置; 分形滤波技术亦可有效地从复杂的地球化学背景中增强弱异常, 并分离出与成矿有关的地球化学异常[6, 9, 15]。但这些已经超出了笔者的叙述范围, 仅就区域地质条件和已知矿点的分布情况来看, (不能排除但)目前没有直接证据表明L1所代表的弱异常主要与上述两种情形有关。因此, 理想的情况是:L3本身就是矿体或近矿围岩, L2为矿致异常, L1为非矿致(弱)异常, 从L1到L2和L3斜率(富集效率)的突变可能意味着这种过渡。
二级异常(这里指L2和L3)进一步刻画了成矿元素的局部富集状态。地层[28]方面, 本区只有元古界地层中Cu的丰度普遍大于T2, 其主要岩性为钙碱性玄武质斜长角闪岩、拉斑玄武质斜长角闪岩、花岗闪长岩、钙碱性玄武质斜长角闪岩、中钾安山岩等; Cu在侏罗系、白垩系中的丰度值略小于30× 10-6, 相应的岩性为杂砂岩、粉砂质页岩、玄武粗安岩; 志留系、奥陶系、震旦系部分层位中Cu的平均含量则与T2基本持平。虽然地层中的Cu对成矿可能有一定的贡献, 特别是花岗质岩浆上升途中往往同化部分含矿物质较高的地层, 并且萃取地层中的Cu, 但一般认为主要的Cu成矿介质应该来源于深部, 并与构造— 岩浆活动密切相关。具体来说, 花岗岩类铜矿化一般都是从源岩获得大量Cu, 而S型(重熔型)岩体中Cu的平均含量通常不会超过20× 10-6, 加之其具有较强的还原性且硫逸度较低, 因此很难形成大规模Cu矿化。Cu矿化一般与I型磁铁矿系列岩体有关[29], 其地球化学继承性显著。如调查[30]显示, 本区I型花岗岩类Cu的丰度为94.26× 10-6, S型、A型分别为7.38× 10-6、9.61× 10-6。如果仅将T1作为异常下限, 那么与Cu矿化无关的建造或岩体可能会被误以为属矿致异常; 另一种情况是, 许多中型以上Cu多金属矿床的主矿体往往沿接触带分布在异常的边缘和外部, 异常的浓集中心位置经常是大面积基性和超基性岩的反映[31], 但类似地质背景或岩石类型在本区并不广泛。
已知长江中下游沿江带是我国著名的Cu、Fe成矿带, 而赣东北地区已发现大型铜矿(德兴斑岩铜矿), 唯有浙西北地区(118° 00'E ~119° 00'E, 28° 40'N ~ 29° 40'N)至今在铜多金属找矿上尚无重大突破。朱玉娣等[32]对比了“ 同时代、近距离” 的浙西桐村斑岩型钼(铜)矿床与赣东北德兴斑岩铜矿床的岩石地球化学特征, 认为桐村矿床位于钱塘拗陷, 而德兴位于江南隆起东段的南缘, 区域构造上受江南隆起和钱塘拗陷之间的赣东北深断裂带控制, 处于断裂带北西侧的隆起区边缘, 暗示德兴岩浆源区更多地受到地幔物质的影响; 桐村矿区成矿物质来源以壳源为主, 因此就矿石品位、矿床规模、矿物物种等方面比较, 二者相差悬殊且桐村矿床总体来说不占优势。然而, 就区域地质条件、物探和化探异常情况[33]来看, 本区都应该是很有希望的远景地区。由T1、T2决定的异常内部结构分区如图4所示, 可见二级异常占整个异常场面积的40%左右, 是进行下一步成矿预测工作的首选靶区, 主要沿马金— 乌镇断裂及其两侧分布(图幅中央偏北的NE向大断裂带)。异常结构的地质意义至少可以看成元素含量在空间上至少存在两个层次嵌套的异常分布, 从而赋予含量排列法以空间属性。
本区以燕山中— 晚期岩浆成矿作用占绝对优势, 侵入体本身主要赋存于背景区和一级异常区, 极个别落入了二级异常区, 有些岩体的边界几乎与一级异常边界完全重合, 这可能与岩浆在上涌过程中与围岩发生的接触交代作用有关。一级异常的发育可能与矿床形成过程中的岩浆岩、沉积岩和变质岩中某些元素的区域同生和后生富集有关, 从而使其有别于周围的地质环境。可见, 控岩和控矿构造主要为NE向及次一级构造裂隙, 岩体、异常及矿点的展布均呈NE走向。一级异常区所占面积较大, 但基本不含矿, 不过可能作为深部存在隐伏矿体的标志, 个别矿点落入了该异常区即为例证。挤压环境不利于成矿作用的发生, 因为挤压会阻碍岩体的侵入, 但在两组断裂的结合部形成的低应力区可以为岩体侵入提供重要的通道, 这些矿点明显就位于这样的结点附近。邱骏挺[34]具体指出, 浙西北地区存在岩浆源区从俯冲导致的加厚地壳榴辉岩相, 向软流圈上涌地壳减薄的麻粒岩相转变的过程, 这种构造转换引起3个效应:上侏罗统岩体氧逸度范围普遍介于MH(磁铁矿一赤铁矿组合)— FMQ (铁橄榄石一磁铁矿一石英组合)之间, 而下白垩统岩体氧逸度则低于FMQ; 上侏罗统岩体沿NE、NW向断裂的交点侵位, 下白垩统岩体沿NE向断裂侵位; NE向断裂从压性转变为张性。这3个效应对区域成矿规律和成矿预测的指示意义有:侏罗系岩体具有较高的氧逸度, 有利于斑岩型Cu、Mo、Au等多金属矿床的形成, 由于构造背景的转换, 白垩系岩体氧逸度降低, 从而不利于Cu成矿; 含矿的侏罗系岩体沿断裂交点侵位, 有利于对矿床进行定位, 相比之下白垩系岩体的构造定位则相对困难; NE向断裂由压性转为张性, 为热液运移提供了通道, 因而白垩系的构造热事件对形成热液型Pb-Zn矿有利, 而不是形成Cu矿。这表明浙西地区存在两种不同的构造背景, 对应着两种不同的成矿环境, 这体现了笔者所圈定出的Cu总异常成因。
二级异常突出了最主要的成矿有利地段, 除个别覆盖层较厚或隐伏矿体外, 几乎所有矿点都落入T2所圈定的二级异常范围内, 这大大缩小了异常查证的范围, 亦证实了关于T2应为矿致异常界限点的推测。总体上, 本区Cu矿化明显受燕山早期二阶段(158~172 Ma)I型中酸性小岩体控制[33], 而大部分矿点分布在以NE向断裂为主体的多组断裂交汇处, 且断裂排布十分密集。相反在一级(弱)异常及背景区域中发育的断裂, 密度和交汇显得十分稀疏。区域东南角出露的断裂全部落入了背景区范围, 说明这些断裂与矿化的关系并不密切。事实上, 这些断裂出露于白垩系地层中, 或者说形成时间应不早于白垩纪, 暗示白垩纪后的断裂活动或与成矿无关, 这与本区很少发现白垩系Cu矿床的事实十分吻合。
总之, 二级异常与区域断裂— 岩浆活动在空间分布上具有更显著的相关性, 晚侏罗世的挤压作用使得含矿的斑岩体沿断裂交汇处侵位形成斑岩型矿床, 而白垩纪的伸展作用使断裂性质由挤压转为拉伸。这种构造背景的转换过程为与热液活动有关的成矿作用提供了十分有利的介质环境[34], 因此沿北东向断裂形成了许多次生的Cu矿化。针对区内桐村、里山岭、双源林等Cu矿化点的野外地质调查显示, 这些矿体经常沿着NE向断裂面分布, 并就位于断层两盘之间, 断面上可见清晰的擦痕及不具有定向性却具有一定磨圆的断层角砾[33, 34], 可作为先挤压后拉张之例证。此外, 二级异常亦涵盖了震旦系、寒武系、奥陶系等古老地层, 以及较年轻的火山岩建造, 虽然地层对于成矿的贡献可能十分有限, 但在这些地层与侵入体的接触带部位已经发现了多个Cu多金属矿化点[33], 呈现出极具潜力的找矿前景。如杨旗坦镇北部平水组与晋宁早期岩浆岩的接触带为重要的赋矿层位; 大墅镇以北地区的个别矿化点明显由中酸性小岩体(岩脉)控制, 矿化均产于岩体(岩脉)的内外蚀变带或近旁围岩中, 可视为一种直接的或间接的找矿标志。二级异常区内大面积出露的荷塘组为一套黑色含碳或碳质页岩、硅质页岩夹石煤层和磷块岩建造, 其中Cu、Ni、V、U、Mo、Zn等含量十分可观[35], 被视为研究区重要的"矿源层"建造。可见, 异常内部结构剖析为区域典型矿床的成因推理和解释等工作提供了重要依据, 理应得到重视。
有趣的是, 大多数矿体及断裂密集交汇处似乎集中分布于一级异常与二级异常的接触带内侧, 但很少有深入二级异常内部的矿点。如果我们的观测具有普遍性, 则另可圈定出一些新的和具有重大战略意义的矿致异常或远景靶区, 如位于开化县城以北、常山县城周围、衢州市区以南、大墅镇以西部分地区出现的异常。关于矿点在二级异常的边缘区集中分布的可能成因, 於崇文[36]认为, 成矿元素的迁移、聚集乃至成矿很可能是在混沌过程中进行的, 其中混沌边缘(edge of chaos)作为介于有序和混沌之间的相变, 系统处于自组织临界状态, 具有最大的复杂性、演化性和创新性, 大型矿床或成矿(区)带往往在混沌的边缘分形生长(fractal growth)。剖析地球化学异常的内部结构并赋予其复杂性内涵, 是笔者长期思考的问题。但至于图 4中一级异常与二级异常的过渡带, 或二级异常的边缘带是否属于混沌边缘, 在缺少其他地质证据和数学证明的前提下不应轻易下结论。
以浙西北地区1:20万Cu元素水系沉积物测量为例, 基于分形求和法对所圈定出的地球化学异常进行了内部结构分析。笔者证明了无标度区掩盖了异常场的内部结构, 继而借鉴前人提出的含量排列法将异常区数据从小到大按顺序等间距排列和自然展示, 并用三段直线(L1、L2、L3)进行拟合, L1为一级异常、L2和L3被归入二级异常。理想的情况是, L3本身就是矿体或近矿围岩, L2则为矿致异常, L1为非矿致异常, L1→ L2、L3斜率(富集效率)的突变可能意味着这种转变, 因此异常结构的地质意义至少可以看成元素含量在空间上至少存在两个层次的异常分布, 由于导致背景场与异常场、一级异常与二级异常的主要地质— 地球化学控制因素不同, 其所形成的元素含量分布图式当然会有所不同。应用表明, 一级弱异常基本不含矿, 可能属于与预测信息无关的干扰信息, 但仍有个别矿点落入该区, 不排除其作为深部存在隐伏矿体标志的可能性; 二级异常近似代表了矿致异常, 或者说最主要的矿化信息或靶区大多集中于二级异常, 与区域断裂— 岩浆活动中心在空间上具有更显著的相关性, 从中强调了岩浆源区、构造背景转换和断裂交汇的控矿意义, 并由此圈定出了一些重点异常作为下一步成矿预测工作的首选靶区。
本文是笔者[18]硕士期间工作的延续。不单是Cu, 其他如Au-Ag、Mo、Sn、W、Pb-Zn等成矿元素的水系沉积物测量均表现为异常大于背景的情形, 这意味着重要的矿床必定位于具有最大地质异常的地段, 但具有最大地质异常地段不一定必然有矿床存在。事实上, 地质异常只是一种必要的成矿背景或成矿基础, 而真正矿床的存在或产生必须考虑控制成矿因素的必要和充分的其它定量因素的组合, 如必要和充分的矿源、必要和充分的驱动成矿元素向有利部位迁移和富集的能源、必要和充分的物理、化学和生物条件使浓集的成矿元素沉淀和堆积、必要和充分的时间和空间使各种成矿元素达到一定规模的聚集等[37]。为此, 剖析地球化学异常的内部结构应具有十分重要的理论和实践意义, 其实质在于结合区域构造— 岩浆活动的时空分布特征尝试区分矿致异常和非矿异常, 进而有效圈定并缩小找矿靶区。然而成矿作用原本就是一个极为复杂的动态过程, 所谓“ 模型” 只是理想的解释其中某一部分现象, 许多问题仍有待于进一步商榷。本区位于钦杭成矿带北缘, 下一步工作可将其与钦杭成矿带南缘某典型成矿区作对比研究, 以检验该模型的适用性和有效性, 这有利于地学数据挖掘与知识发现。
附录:基于MATLAB平台的分形求和模型
输入原始数组 y
y=sort(y, 'ascend'); % 排序从小到大
RR=y; % y变为R, R为尺度
L=20; % 输入步长L
ii=1;
[UFO, USO]= size(RR);
% R= zeros(UFO, USO);
for list=1:L:UFOLOVE=RR(list, 1);
yy(ii, 1)=LOVE;
ii=ii+1;
end
yy;
R=yy;
[a, b]=size(R); % a=总数, b=1
N=zeros(a, b);
for i=1:1:a
k=0;
for j=1:1:a
if yy(j, 1)> =R(i, 1) % 大于等于尺度R的数值搜索
k=k+yy(j, 1); % k 为累积频率
% k=k+1;
end
end
N(i, 1)=k; % 求得的累加频率归入N序列
end
R=log(R); % R为尺度
N=log(N); % N为累积频率
plot(R, N, 'ok')
hold on
%最优的分界点采取全搜索, 范围是第二个和倒数第二个点
outlier=[2, a-1];
b=polyfit(R, N, 1);
%计算残差
N11=polyval(b, R);
error0=sum((N11-N).^2); %计算拟合残差
u=mean(N);
Sumerror=sum((N-u).^2); %计算总离差
fit=1-error0/Sumerror;
for i=outlier(1, 1):outlier(1, 2)
N1=N(1:i, 1);
R1=R(1:i, 1);
N2=N(i+1:end, 1);
R2=R(i+1:end, 1);
b1=polyfit(R1, N1, 1);
b2=polyfit(R2, N2, 1);
u1=mean(N1);
u2=mean(N2);
Sumerror1=sum((N1-u1).^2);
Sumerror2=sum((N2-u2).^2);
N11=polyval(b1, R1);
N22=polyval(b2, R2);
error1=sum((N11-N1).^2);
error2=sum((N22-N2).^2);
error=error1+error2;
if error< =error0
error0=error;
b=[b1; b2];
threshold=yy(i, 1);
k=i;
fit1=1-error1/Sumerror1;
fit2=1-error2/Sumerror2;
end
end
t1=[R(1, 1):0.01:R(k, 1)];
t2=[R(k+1, 1):0.01:R(a, 1)];
Y1=polyval(b(1, :), t1);
Y2=polyval(b(2, :), t2);
plot(t1, Y1, 'k', t2, Y2, 'k')
% grid on
xlabel('log r');
ylabel('log N(r)');
b
threshold
fit1;
fit2;
k;
grid on
xlabel('log r');
ylabel('log N(r)');
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|





