基于Metropolis抽样的弹性阻抗随机反演

引用本文

孙瑞莹, 印兴耀, 王保丽, 张广智. 基于Metropolis抽样的弹性阻抗随机反演[J]. 物探与化探, 2015,39(1): 203-210.
SUN Rui-Ying, YIN Xing-Yao, WANG Bao-Li, ZHANG Guang-Zhi. Stochastic inversion of elastic impedance based on Metropolis sampling algorithm[J]. Geophysical and Geochemical Exploration, 2015,39(1): 203-210. 复制到剪切板

Doi:10.11720/wtyht.2015.1.33
Permissions

《物探与化探》编辑部所有

基于Metropolis抽样的弹性阻抗随机反演

孙瑞莹, 印兴耀, 王保丽, 张广智

中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

作者简介: 孙瑞莹(1988-),女,硕士研究生,主要从事地球物理领域随机地震反演方法的研究。

收稿日期: 2014-05-08

基金: 国家重点基础研究发展计划(973计划)(2013CB228604); 国家科技重大专项项目(2011ZX05030-004-002); 国家自然科学基金项目(41204085); 中国石化地球物理重点实验室项目(WTYJY- WX2013-04-07)

摘要

笔者提出了基于Metropolis抽样的弹性阻抗随机反演方法,该方法是一种基于蒙特卡洛的非线性反演方法,能够有效地融合测井资料中的高频信息,提高反演结果的分辨率。应用贝叶斯理论框架,首先通过快速傅里叶滑动平均模拟算法(fast Fourier transform-moving average,FFT-MA)和逐渐变形算法(gradual deformation method,GDM)得到基于地质统计学的先验信息,然后用Metropolis抽样算法对后验概率密度进行抽样,得到反演问题的解。其中FFT-MA模拟作为一种高效的频率域模拟方法,结合GDM后,在保持模拟空间结构不变的前提下,可以连续修改储层模型,直至满足实际观测地震记录。数值试验表明:FFT-MA模拟有效地提高了计算效率,融入GDM更新算法,可以保证反演结果有效地收敛,并且反演结果与理论模型吻合较好,具有较高的分辨率,该方法采用两步法反演弹性参数,运算速度较快。

关键词: 快速傅里叶滑动平均模拟算法; 逐渐变形算法; 弹性阻抗; 高分辨率; Metropolis抽样

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)01-0203-08

Stochastic inversion of elastic impedance based on Metropolis sampling algorithm

SUN Rui-Ying, YIN Xing-Yao, WANG Bao-Li, ZHANG Guang-Zhi

School of Geosciences,China University of Petroleum(Huadong),Qingdao 266580,China

Abstract

Stochastic inversion of elastic impedance based on Metropolis sampling algorithm is a Monte Carlo based strategy for non-linear inversion,which can effectively integrate the high-frequency information of well-logging data and have a higher resolution.This method is formulated in the Bayesian framework.Firstly,the priori information can be obtained through Fast Fourier Transform-Moving Average (FFT-MA) and Gradual Deformation Method (GDM).Then Metropolis algorithm is employed so as to obtain an exhaustive characterization of the posteriori probability density.FFT-MA is a kind of efficient simulation method.Combined with GDM,it can constantly modify the reservoir model and keep the spatial structure unchanged until it matches the observed seismic data.According to the numerical calculations,it can be concluded that FFT-MA simulation can reduce the time consumption.Combined with GDM updating algorithm,the inversion results can converge rapidly,and the final results match the model well and have a higher resolution.In addition,this method adopts two-step method to invert elastic parameters,so it improves the computational efficiency to some extent.

Keyword: FFT-MA; GDM; elastic impedance; high-resolution; Metropolis sampling

Show Figures

地震勘探已经从简单的构造识别转向复杂构造、薄储层以及老油田剩余油的研究。勘探难度的加大, 也对能得到更高信噪比和分辨率的地震资料提出了挑战。Chopra等发现实际的地震子波主频大约在30 Hz, 很难区分25 m以下的薄层顶底^[1]。但是, 工业目标地质体的厚度一般在10 m甚至10 m以下, 所以提高分辨率以反演薄层信息, 在储层识别和油藏描述中起到了重要的作用, 并且随着地球物理研究的深入及反演精度的提高, 非线性反演方法更容易得到真值。

随机反演在储层识别和油藏描述中具有重要作用。许多学者对确定性反演和随机反演进行了研究对比^{[2, 3, 4, 5, 6]}, 结果表明, 确定性反演可以给出唯一的局部平滑估计, 而随机反演方法则提供了多个反演解, 并且同时满足实际观测地震数据和测井数据, 能合理估计并反映出确定性反演中被平滑掉的不确定性。相比随机反演, 确定性反演方法具有计算速度快、计算量小的特点, 因此应用范围更广, 而随机反演由于计算速度慢、需要慎重解释多个反演结果等原因, 使用范围比较小^[7]。但是近些年, 由于随机反演能够在空间相关性和井约束下, 模拟出地震频带以外的信息, 分辨率高于常规的确定性反演方法, 随机反演又逐渐被人们所关注。而弹性阻抗反演采用叠前角度部分叠加道集, 反演过程中考虑了子波随偏移距的变化, 相比叠后波阻抗反演更能反映地层岩性和流体特征, 比叠前AVO反演方法的抗噪能力更强, 因而在地震勘探领域具有广泛应用。1999年, Connolly^[8]发表弹性阻抗的文章后, 在国内外地球物理学界掀起了弹性阻抗反演研究的热潮, 提出了许多扩展的弹性阻抗概念, 并对阻抗域的储层预测和流体识别等做了大量的分析研究^{[9, 10, 11, 12, 13, 14]}。于是为了提高反演结果的抗噪性和分辨率, 笔者提出了基于Metropolis抽样的弹性阻抗随机反演方法, 由于采用两步法进行反演, 在一定程度上提高了计算效率。

Kjø nsberg等人^[15]建议用贝叶斯方法进行反演, 以获取后验概率密度的样本, 这里假定基于地质统计学的先验信息和似然函数都服从高斯分布, 那么乘积得到的后验信息就是非高斯分布, 即不能得到后验概率密度的解析解。对于后验概率密度无法用公式表达的情况, 需要对后验概率密度进行抽样来求解反演问题, 笔者采用Metropolis准则进行抽样运算。基于蒙特卡洛抽样的反演方法结合了Metropolis算法、FFT-MA模拟算法^[16]和GDM更新算法^[17], 可以为先验信息提供多参数扰动。通过对模型数据的对比试算可以发现, 基于Metropolis抽样的弹性阻抗随机反演方法是可行的。

1 方法原理

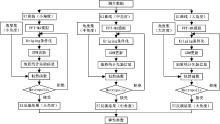
笔者利用贝叶斯理论寻找反演问题的解。由于先验概率密度和似然函数都服从高斯分布, 那么乘积得到的后验概率密度就是非高斯分布, 所以不能得到其解析解, 此时必须通过对后验概率密度进行抽样得到反问题的解。从高维概率密度得到样本的一种方法是利用Metropolis抽样算法, 基本思路就是通过FFT-MA模拟得到三个角度弹性阻抗体的高斯先验概率密度, 然后通过GDM算法扰动更新先验信息, 最后利用Metropolis算法对后验概率密度进行抽样, 得到反演的三个弹性阻抗体, 随后就可以从弹性阻抗体中提取所需的弹性参数。文中提出的基于Metropolis抽样的弹性阻抗随机反演流程如图1所示。

	Figure Option View Download New Window
	图1 基于Metropolis抽样的弹性阻抗随机反演流程

1.1 弹性阻抗反演方法

Connolly^[8]根据Zoeppritz方程给出了弹性阻抗的表达式

$\begin{matrix} I_{e} (θ) = α^{(1 + ta n^{2} θ)} β^{- 8 Ksi n^{2} θ} ρ^{(1 - 4 Ksi n^{2} θ)} 。 (1) \end{matrix}$

为了消除入射角变化对尺度的影响, Whitcombe^[9]对Connolly方程进行了标准化处理。引入三个参考常数α ₀、β ₀和ρ ₀, 并把I_e函数修改为

$\begin{matrix} I_{e} (θ) = α_{0} ρ_{0} [{(\frac{α}{α_{0}})}^{1 + ta n^{2} θ} {(\frac{β}{β_{0}})}^{- 8 Ksi n^{2} θ} {(\frac{ρ}{ρ_{0}})}^{1 - 4 Ksi n^{2} θ}], \end{matrix}$ (2)

其中:α 、β 和ρ 分别为纵波速度、横波速度和密度; θ 为入射角; K=β ²/α ²; α ₀、β ₀和ρ ₀分别为纵波速度、横波速度和密度的均值。

叠前弹性阻抗反演的基本思路是利用纵波弹性阻抗构造纵波反射系数

$\begin{matrix} R (θ) = \frac{I_{e 2} (θ) - I_{e 1} (θ)}{I_{e 2} (θ) + I_{e 1} (θ)}, \end{matrix}$ (3)

然后利用与叠后反演相类似的反演算法计算不同入射角度的弹性阻抗剖面, 进而由弹性阻抗剖面提取所需的弹性参数。地震道S是反射系数R和子波W的褶积, 对于与角度相关的数据, 褶积模型可以写成

$\begin{matrix} S (θ) = R (θ) * W (θ), \end{matrix}$ (4)

其中:S(θ )为角度地震道; R(θ )是角度反射系数, 可通过测井的纵波速度、横波速度和密度, 由Zoeppritz方程计算得到; W(θ )是角度子波, 通过反射系数和角道集地震资料获得。就像对反射系数R进行积分得到声阻抗一样, 角度反射系数可用来计算弹性阻抗。弹性阻抗I_e并不是一个可以进行物理测量的属性, 它是通过推导得出的用来解释地震数据的属性。

从I_e(θ )中提取P波速度、S波速度及密度等参数的过程和弹性阻抗反演一样, 均是叠前反演中重要的一环。提取这些参数需对式(2)进行求解, 由于此方程式是非线性的, 若直接求解, 势必带来不少的麻烦, 为此可将式(2)进行变换

$\begin{matrix} \ln \frac{I_{e} (θ)}{I_{e 0}} = (1 + ta n^{2} θ) \ln \frac{α}{α_{0}} + (- 8 Ksi n^{2} θ) \ln \frac{β}{β_{0}} + (1 - 4 Ksi n^{2} θ) \ln \frac{ρ}{ρ_{0}} 。 \end{matrix}$ (5)

为得到lnα 、lnβ 和lnρ , 需三个不同角度的弹性阻抗体。将三个角度值分别代入式(5)可以得到方程组

$\begin{matrix} \{\begin{matrix} \ln \frac{I_{e} (θ_{1})}{I_{e 0}} = (1 + ta n^{2} θ_{1}) \ln \frac{α}{α_{0}} + (- 8 Ksi n^{2} θ_{1}) \ln \frac{β}{β_{0}} + (1 - 4 Ksi n^{2} θ_{1}) \ln \frac{ρ}{ρ_{0}}, \\ \ln \frac{I_{e} (θ_{2})}{I_{e 0}} = (1 + ta n^{2} θ_{2}) \ln \frac{α}{α_{0}} + (- 8 Ksi n^{2} θ_{2}) \ln \frac{β}{β_{0}} + (1 - 4 Ksi n^{2} θ_{2}) \ln \frac{ρ}{ρ_{0}}, \\ \ln \frac{I_{e} (θ_{3})}{I_{e 0}} = (1 + ta n^{2} θ_{3}) \ln \frac{α}{α_{0}} + (- 8 Ksi n^{2} θ_{3}) \ln \frac{β}{β_{0}} + (1 - 4 Ksi n^{2} θ_{3}) \ln \frac{ρ}{ρ_{0}} 。 \end{matrix} (6) \end{matrix}$

用矩阵形式可表示为

$\begin{matrix} [\begin{matrix} 1 + ta n^{2} θ_{1} & - 8 Ksi n^{2} θ_{1} & 1 - 4 Ksi n^{2} θ_{1} \\ 1 + ta n^{2} θ_{2} & - 8 Ksi n^{2} θ_{2} & 1 - 4 Ksi n^{2} θ_{2} \\ 1 + ta n^{2} θ_{3} & - 8 Ksi n^{2} θ_{3} & 1 - 4 Ksi n^{2} θ_{3} \end{matrix}] [\begin{matrix} \ln \frac{α}{α_{0}} \\ \ln \frac{β}{β_{0}} \\ \ln \frac{ρ}{ρ_{0}} \end{matrix}] = [\begin{matrix} \ln \frac{I_{e} (θ_{1})}{I_{e 0}} \\ \ln \frac{I_{e} (θ_{2})}{I_{e 0}} \\ \ln \frac{I_{e} (θ_{3})}{I_{e 0}} \end{matrix}] 。 \end{matrix}$ (7)

若直接对方程组进行求解, 所得到的lnα 、lnβ 和lnρ 值在某些采样点处极不稳定, 并且可能与实际的物理和地质意义相悖。为此, 还需将上式作进一步变换。角度相同时, 各采样点的同一岩性参数(ln(α /α ₀)、ln(β /β ₀)和ln(ρ /ρ ₀))所对应的系数值相同, 它们不随时间变化。因此, 可将上式写成

$\begin{matrix} [\begin{matrix} \ln \frac{ρ (t_{1})}{ρ_{0}} & \ln \frac{α (t_{1})}{α_{0}} & \ln \frac{β (t_{1})}{β_{0}} \\ \ln \frac{ρ (t_{2})}{ρ_{0}} & \ln \frac{α (t_{2})}{α_{0}} & \ln \frac{β (t_{2})}{β_{0}} \\ ︙ & ︙ & ︙ \\ \ln \frac{ρ (t_{n})}{ρ_{0}} & \ln \frac{α (t_{n})}{α_{0}} & \ln \frac{β (t_{n})}{β_{0}} \end{matrix}] [\begin{matrix} 1 + ta n^{2} θ \\ - 8 Ksi n^{2} θ \\ 1 - 4 Ksi n^{2} θ \end{matrix}] = [\begin{matrix} \ln \frac{I_{e} (t_{1}, θ)}{I_{e 0}} \\ \ln \frac{I_{e} (t_{2}, θ)}{I_{e 0}} \\ ︙ \\ \ln \frac{I_{e} (t_{n}, θ)}{I_{e 0}} \end{matrix}] 。 \end{matrix}$ (8)

由于在提取岩性参数时所用的弹性阻抗体来自于反演, 因此, 可选取反演得到的井旁道弹性阻抗数据和井曲线(纵波曲线、横波曲线和密度曲线)来建立上面的关系, 这种岩性参数与弹性阻抗之间的关系最为密切。另外, 可以根据弹性阻抗反演方法直接反演得到拉梅参数、剪切模量和流体因子等其他反映岩性和流体的参数, 如表1所示^[18], 选取不同的AVO近似式, 就可以得到不同的反演参数。

表1 常见弹性阻抗方程、反演的岩性参数和方程推导的AVO近似式^[18]

弹性阻抗方程	岩性参数	AVO近似式
I_e(θ )=I_e0( $\begin{matrix} \frac{α}{α_{0}} \end{matrix}$ )^a( $\begin{matrix} \frac{β}{β_{0}} \end{matrix}$ )^b( $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$ )^c	纵波速度α 、横波速度β 、密度ρ	Zoeppritz方程
I_e(θ )=A₀( $\begin{matrix} \frac{λ}{λ_{0}} \end{matrix}$ )^a( $\begin{matrix} \frac{μ}{μ_{0}} \end{matrix}$ )^b( $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$ )^c	拉梅常数λ 、剪切模量μ 、密度ρ	R(θ )= $\begin{matrix} [\frac{1}{4} - \frac{1}{2} {(\frac{β}{α})}^{2}] \end{matrix}$ sec²θ $\begin{matrix} \frac{Δα}{α} \end{matrix}$ + $\begin{matrix} {(\frac{β}{α})}^{2} \end{matrix} \begin{matrix} (\frac{1}{2} se c^{2} θ - 2 si n^{2} θ) \end{matrix} \begin{matrix} \frac{Δμ}{μ} \end{matrix}$ + $\begin{matrix} \frac{1}{4} \end{matrix}$ (1-tan²θ ) $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$
I_e(θ )=I_p0( $\begin{matrix} \frac{I_{p}}{I_{p 0}} \end{matrix}$ )^a( $\begin{matrix} \frac{I_{s}}{I_{s 0}} \end{matrix}$ )^b( $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$ )^c	纵波阻抗I_p、横波阻抗I_s、密度ρ	R(θ )= $\begin{matrix} \frac{se c^{2} θΔ I_{p}}{2 I_{p}} \end{matrix}$ -4 $\begin{matrix} \frac{β^{2}}{α^{2}} \end{matrix}$ sin²θ $\begin{matrix} \frac{Δ I_{s}}{I_{s}} \end{matrix}$ +4 $\begin{matrix} \frac{β^{2}}{α^{2}} \end{matrix}$ sin²θ $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$
I_e(θ )=I_EF0( $\begin{matrix} \frac{f}{f_{0}} \end{matrix}$ )^a( $\begin{matrix} \frac{μ}{μ_{0}} \end{matrix}$ )^b( $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$ )^c	流体项f、剪切模量μ 、密度ρ	R(θ )= $\begin{matrix} [(\frac{1}{4} - \frac{γ_{dry}^{2}}{4 γ_{sat}^{2}}) se c^{2} θ] \end{matrix} \begin{matrix} \frac{Δf}{f} \end{matrix}$ + $\begin{matrix} (\frac{γ_{dry}^{2}}{4 γ_{sat}^{2}} se c^{2} θ - \frac{2}{γ_{sat}^{2}} si n^{2} θ) \end{matrix} \begin{matrix} \frac{Δμ}{μ} \end{matrix}$ + $\begin{matrix} \frac{1}{4} \end{matrix}$ (1-tan²θ ) $\begin{matrix} \frac{ρ}{ρ_{0}} \end{matrix}$

表1 常见弹性阻抗方程、反演的岩性参数和方程推导的AVO近似式^[18]

表1中:a=1+tan²θ ; b=-8(β /α )²sin²θ ; c=1-4(β /α )²sin²θ ; I_e0, A₀, I_p0和I_EF0分别为相应的反演参数的均值。

1.2 随机反演理论

在贝叶斯框架下进行反演问题的求解, 假设噪声(似然函数)和先验分布均服从高斯分布, 根据贝叶斯理论^[19]

$\begin{matrix} σ_{M} (m) = k ρ_{M} (m) L (d / m) 。 (9) \end{matrix}$

其中:ρ _M(m)表示地质统计先验信息; L(d/m)代表似然函数, 表示模型与数据的匹配程度; σ _M(m)就是贝叶斯后验分布。

1.2.1 基于地质统计学的先验信息

FFT-MA模拟能够产生基于地质统计先验信息的概率密度的抽样, 并且可以对于给定的先验样本评估其似然函数。为了获得有效的样本信息, 必须控制先验概率密度的微扰, 笔者引入GDM更新算法对FFT-MA模拟结果进行扰动结合FFT-MA算法和GDM算法获得先验信息, 这就是所谓的基于地质统计学的先验信息。

(1)FFT-MA算法。FFT-MA算法是一种基于地质统计学的频率域模拟方法。不同于以往的时域随机模拟方法, 它能够分离模拟过程中所需要的空间结构项和随机项, 便于保证空间结构不变的情况下对随机项进行扰动, 利于结合优化算法对反问题进行求解。

FFT-MA方法通过快速傅里叶变换(FFT)简化了Oliver^[20]提出的滑动平均(MA)模拟方法的计算, 表达式可以简要表示为

$\begin{matrix} y = m + g * z, \end{matrix}$ (10)

式中:g* $\begin{matrix} \overset{̅}{g} \end{matrix}$ =C, 且C(h)=σ ²-γ (h); y表示模拟结果; m表示均值; σ 表示标准差; g表示协方差函数C的共轭根; z表示符合模拟维度的随机高斯白噪声。实际上高斯随机场是通过FFT算法将g转换到傅氏域得到的。FFT-MA模拟能够重构出满足指定变差结构和指定网格大小的数据, 但由于它是一种非条件模拟方法, 不满足硬数据(已知井资料), 在实际应用时采用Journel和Huijbregts^[21]提出的克里金条件化方法进行条件化处理, 从而该方法完全可以和经典的序贯模拟方法相媲美, 并可有效地克服经典的序贯模拟方法计算耗时、耗内存等问题, 提高反演方法的计算效率。

(2)GDM更新算法。传统的随机反演方法在进行模拟时, 即使达到了Metropolis准则的接受条件, 也不能保证模拟结果一定会使目标函数收敛。笔者在利用FFT-MA模拟提高计算效率的同时, 引入了逐步变形更新算法, 以保证模拟搜索的收敛性, 从而达到提高反演精度的目的。

GDM最早由Hu等^[22]提出, 用来逐步修改高斯分布的储层模型, 其后被扩展到非高斯分布的序贯指示模拟^[23]。GDM算法可以简要表示为两个独立的高斯随机函数的线性组合

$\begin{matrix} z_{propose} = z_{current} \cos (πp) + z_{new} \sin (πp), (11) \end{matrix}$

其中:p的取值范围为0~1/2; z_propose、z_current和z_new分别为更新的白噪、当前待更新的白噪和加入的新白噪。由于高斯白噪z的存在使得FFT-MA算法具有随机性, 不管模拟网格的大小, 只需要对变形参数进行扰动就可以修改整个模型, 但由于协方差结构C不改变, 这种扰动不会影响数据的空间变差结构。扰动区域和p值是随机给定的, 因此可以根据需要调整这些参数, 提高Metropolis算法的接受概率, 以节省计算时间。

1.2.2 似然函数

对高维概率密度进行抽样时所使用的Metropolis准则中, 需要应用似然函数计算接受概率, 似然函数采用

$\begin{matrix} \begin{matrix} L (d / m) = \\ kexp [- \frac{1}{2} \overset{N}{\sum_{i = 1}} \frac{(d^{i} - d_{obs}^{i})^{2}}{σ^{2}} - α \overset{N}{\sum_{i = 1}} (m^{i} - m_{0}^{i})^{2}], \end{matrix} \end{matrix}$ (12)

其中:dⁱ代表模拟地震波形的振幅, 可由反射系数求得; $\begin{matrix} d_{obs}^{i} \end{matrix}$ 是观测数据的采样点; σ 是期望数据不确定性的标准差; mⁱ代表弹性阻抗体; $\begin{matrix} m_{0}^{i} \end{matrix}$ 是根据测井资料计算的EI曲线的平滑模型约束; α 是可调因子。这样, 结合基于地质统计学的高频先验信息和基于确定性反演的低频平滑约束信息, 得到宽频带的反演结果, 可以克服子波的带限性质引起的频率缺失问题。另外, 直接采用精确的Zoeppritz方程计算正演合成地震记录, 减少了Zoeppritz方程近似所引起的误差。

1.2.3 Metropolis抽样

Metropolis抽样是一种基于蒙特卡洛的抽样方法^[24]。假定先验信息和似然函数都服从高斯分布, 那么乘积得到的后验信息就是非高斯分布, 对于这种后验概率密度无法用公式表达的情况, 需要对后验概率密度进行抽样来求解反问题。采用Metropolis抽样算法, 接受准则可表示为

$\begin{matrix} P_{accept} = \{\begin{matrix} 1, L (m_{propose}) < L (m_{accept}), \\ \exp (\frac{- ΔL}{kT}), L (m_{propose}) \geq L (m_{accept}) 。 \end{matrix} (13) \end{matrix}$

其中:L是似然函数; m_accept是先前接受模型; m_propose是先前接受模型的扰动信息; Δ L=L(m_propose)-L(m_accept), k和T是可调参数; P_accept是后验概率密度的接受概率。

Gelman等人发现, 高维分布的接受概率约为23%^[25], 所以应该调整各参数, 例如GDM扰动区域、GDM算法中p的取值、变差函数的选取、Metropolis接受准则的常数k和温度T等, 使接受概率保持在23%左右。这样就可以结合FFT-MA模拟、GDM扰动更新、似然函数的建立和Metropolis接受准则来判断接受概率, 直至满足收敛条件。

综上, 在贝叶斯理论框架下, 首先通过FFT-MA谱模拟方法得到高斯概率密度, 利用GDM算法扰动更新模拟实现得到基于地质统计学的先验信息; 然后引入确定性反演中的低频平滑约束信息构建似然函数; 最后利用Metropolis算法对后验概率密度进行抽样得到弹性阻抗体, 进而可由弹性阻抗体中提取所需的弹性参数。

2 模型测试与分析

2.1 一维数据测试

选用一维数据进行测试, 该数据体是某井的真实测井资料。图2a为反演的弹性阻抗与模型数据的对比, 图2b为由图2a所示的弹性阻抗体中提取的纵波速度、横波速度以及密度与模型数据的对比。从图中可以看出, 弹性阻抗的反演结果与模型数据比较吻合, 并且提取的弹性参数比较可信, 与模型数据基本一致。图3为信噪比为1时得到的反演结果与模型数据的对比, 可以看出即使存在噪声的情况下, 反演的弹性阻抗体和提取的弹性参数均比较可信。

	Figure Option View Download New Window
	图2 一维模型下弹性阻抗(a)及弹性参数(b)反演结果与模型对比

	Figure Option View Download New Window
	图3 一维模型下信噪比为1时弹性阻抗(a)及弹性参数(b)反演结果与模型对比

2.2 二维模型试算

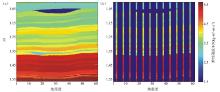
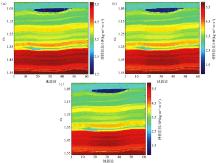
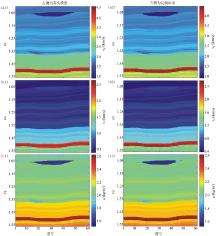
采用Marmousi2模型的一部分进行二维反演算法的测试与分析, 其中图4a为模型数据, 图4b为抽取的12口伪井(随机反演要求井密度越大越好, 故这里选取较多的伪井进行反演)。图5为利用图4b所示的12口伪井得到地质统计先验信息, 在小角度、中角度和大角度的弹性阻抗反演结果(图5), 与图4a对比可以看出, 弹性阻抗反演结果与模型数据基本吻合, 并且可以识别图中的薄层。图6为由反演的三个弹性阻抗体提取的纵波速度、横波速度和密度与模型参数的对比, 可以看出反演结果与模型参数比较相似, 反演效果较好。

	Figure Option View Download New Window
	图4 Marmousi2模型部分数据(a)及抽取的12口伪井(b)

	Figure Option View Download New Window
	图5 小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果

	Figure Option View Download New Window
	图6 反演的弹性阻抗体提取的弹性参数 a1, a2— 纵波速度; b1, b2— 横波速度; c1, c2— 密度

3 结论和认识

应用贝叶斯框架进行基于Metropolis抽样的弹性阻抗随机反演, 对后验概率密度进行抽样就可以得到反演问题的解。笔者结合FFT-MA算法和GDM更新算法得到基于地质统计学的先验信息, 引入Metropolis算法对后验概率密度进行抽样, 得到反演问题的解。相比确定性反演, 随机反演结果的分辨率较高。并且该反演方法运算速度较快, 首先FFT-MA模拟方法较常规模拟方法的计算效率高; 其次, 弹性阻抗反演采用的是两步法, 进一步提高了计算效率。通过资料分析可知, 基于Metropolis抽样的弹性阻抗随机反演可以得到有效的弹性阻抗数据体, 且提供合理的弹性参数信息。反演结果的分辨率较高, 即使信噪比较小时, 仍然可以得到合理的弹性参数信息, 从而证明了该方法的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chopra S, Castagna J, Portniaguine O. Seismic resolution and thin-bed reflectivity inversion[J]. CSEG recorder, 2006, 31(1): 19-25. [本文引用:1]
[2]	Sancevero S S, Remacre A Z, de Souza Portugal R, et al. Comparing deterministic and stochastic seismic inversion for thin-bed reservoir characterization in a turbidite synthetic reference model of Campos Basin, Brazil[J]. The Leading Edge, 2005, 24(11): 1168-1172. [本文引用:1]
[3]	Moyen R, Doyen P M. Reservoir connectivity uncertainty from stochastic seismic inversion[C]//2009 SEG Annual Meeting Society of Exploration Geophysicists, 2009. [本文引用:1]
[4]	Sams M S, Saussus D. Comparison of uncertainty estimates from deterministic and geostatistical inversion[C]//70^th EAGE Conference & Exhibition, 2008. [本文引用:1]
[5]	Francis A M. Understand ing stochastic inversion: part 1[J]. First Break, 2006, 24(11): 69-77. [本文引用:1]
[6]	Francis A M. Understand ing stochastic inversion: part 2[J]. First Break, 2006, 24(12): 79-84. [本文引用:1]
[7]	Dubrule O. Workshop report: 'Uncertainty in reserve estimates' EAGE Conference, Amsterdam[J]. Petroleum Geoscience, 1996, 2(4): 351-352. [本文引用:1]
[8]	Connolly P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. [本文引用:2]
[9]	Whitcombe D N. Elastic impedance normalization[J]. Geophysics, 2002, 67(1): 60-62. [本文引用:2]
[10]	Whitcombe D N. Extended elastic impedance for fluid and lithology prediction[J]. Geophysics, 2002, 67(1): 63-67. [本文引用:1]
[11]	甘利灯, 赵邦六, 杜文辉, 等. 弹性阻抗在流体与岩性预测中的潜力分析[J]. 石油物探, 2005, 44(5): 504-508. [本文引用:1]
[12]	王保丽, 印兴耀, 张繁昌. 弹性阻抗反演及应用研究[J]. 地球物理学进展, 2005, 20(1): 89-92. [本文引用:1]
[13]	潘仁芳, 宋鹏. 叠前弹性反演在苏里格气田的应用[J]. 物探与化探, 2010, 34(2): 237-241. [本文引用:1]
[14]	张广智, 郑静静, 印兴耀, 等. 基于Curvelet变换的角度流体因子提取技术[J]. 物探与化探, 2011, 35(4): 505-510. [本文引用:1]
[15]	Kjønsberg H, Hauge R, Kolbjørnsen O, et al. Bayesian Monte Carlo method for seismic predrill prospect assessment[J]. Geophysics, 2010, 75(2): O9-O19. [本文引用:1]
[16]	Le Ravalec M, Noetinger B, Hu L Y. The FFT moving average (FFT-MA) generator: An efficient numerical method for generating and conditioning Gaussian simulations[J]. Mathematical Geology, 2000, 32(6): 701-723. [本文引用:1]
[17]	Hu L Y. Gradual deformation and iterative calibration of Gaussian-related stochastic models[J]. Mathematical Geology, 2000, 32(1): 87-108. [本文引用:1]
[18]	桂金咏, 印兴耀, 曹丹平. 基于弹性阻抗反演理论的泊松比反演方法研究[J]. 石油物探, 2011, 50(5): 463-469. [本文引用:1]
[19]	Scales J A, Smith M L, Treitel S. Introductory geophysical inverse theory[M]. Samizdat Press, 2001. [本文引用:1]
[20]	Oliver D S. Moving averages for Gaussian simulation in two and three dimensions[J]. Mathematical Geology, 1995, 27(8): 939-960. [本文引用:1]
[21]	Journel A G, Huijbregts C J. Mining geostatistics[M]. Academic press, 1978. [本文引用:1]
[22]	Hu L Y, Blanc G. Constraining a reservoir facies model to dynamic data using a gradual deformation method[C]//6^th European Conference on the Mathematics of Oil Recovery, 1998. [本文引用:1]
[23]	Hu L Y, Le Ravalec M, Blanc G, et al. Reducing uncertainties in production forecasts by constraining geological modeling to dynamic data[C]//SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 1999. [本文引用:1]
[24]	Mosegaard K, Tarantola A. Monte Carlo sampling of solutions to inverse problems[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1995, 100(B7): 12431-12447. [本文引用:1]
[25]	Gelman A, Roberts G, Gilks W. Efficient metropolis jumping hules[J]. Bayesian statistics, 1996, 5: 599-608. [本文引用:1]

2006

0.0

... Chopra等发现实际的地震子波主频大约在30 Hz,很难区分25 m以下的薄层顶底^[1] ...

2005

0.0

... 许多学者对确定性反演和随机反演进行了研究对比^[2,3,4,5,6],结果表明,确定性反演可以给出唯一的局部平滑估计,而随机反演方法则提供了多个反演解,并且同时满足实际观测地震数据和测井数据,能合理估计并反映出确定性反演中被平滑掉的不确定性 ...

2009

0.0

2008

0.0

2006

0.0

2006

0.0

1996

0.0

... 相比随机反演,确定性反演方法具有计算速度快、计算量小的特点,因此应用范围更广,而随机反演由于计算速度慢、需要慎重解释多个反演结果等原因,使用范围比较小^[7] ...

1999

0.0

... 1999年,Connolly^[8]发表弹性阻抗的文章后,在国内外地球物理学界掀起了弹性阻抗反演研究的热潮,提出了许多扩展的弹性阻抗概念,并对阻抗域的储层预测和流体识别等做了大量的分析研究^{[9,10,11,12,13,14]} ...

... 1 弹性阻抗反演方法Connolly^[8]根据Zoeppritz方程给出了弹性阻抗的表达式 ...

2002

0.0

... 为了消除入射角变化对尺度的影响,Whitcombe^[9]对Connolly方程进行了标准化处理 ...

2002

0.0

2005

0.0

2005

0.0

王保丽, 印兴耀, 张繁昌. 弹性阻抗反演及应用研究[J]. 地球物理学进展, 2005, 20(1): 89-92.

The post\|stack inversion can’t obtain reliable impedance and other lithologic information. This paper does analysis on an area seismic data using elastic impedance inversion theory. The case indicates that elastic impedance inversion can obtain ideal inversion result and from the inverted impedance section we can extract lithologic parameters which can reflect lithology and fluid character. More information and higher revolntion than traditional invevsion are obtained through the elastic impedance inversion, and it is more quantitative and fast than AVO inversion.

利用常规叠后波阻抗反演方法不能得到可靠的波阻抗和其它岩性信息.本文运用弹性阻抗反演理论对某地区的地震资料进行了分析研究，应用实例表明，用弹性阻抗反演方法可得到较理想的反演结果，且从反演所得到的波阻抗剖面中能提取出许多岩性参数，这些岩性参数能反映岩性和流体特征.与传统的波阻抗反演相比，弹性阻抗反演具有信息量丰富、分辨率高的特点；与定性的AVO反演相比，该方法达到了定量的程度，而且速度快.

2010

0.0

潘仁芳, 宋鹏. 叠前弹性反演在苏里格气田的应用[J]. 物探与化探, 2010, 34(2): 237-241.

In Sulige area，when gas saturation is lower than 70%, the change of Poisson's ratio is not obvious, and the application of AVO technique to detecting gas potential does not yield satisfactory result. The elastic impedance method based on Fatti approximation uses prestack data for inversion and includes abundant lithologic and fluid information. Nevertheless, its shortcomings in the aspects of the unstable solution in small angles and the low inversion precision built in wet rock background are also very obvious. The improved Fatti approximation formula is more stable, and its inversion precision built in the known regional rock property relationships between variables for the background case is raised. Practice demonstrates that the application of the crossplot of LambdaMuRho attributes extracted from the elastic impedance inversion volume is very effective in low gas saturation detection in Sulige area，as evidenced by the clear reflection of the reservoir information.

苏里格气田当含气饱和度小于70%时，泊松比变化不明显，用AVO方法进行含气性检测效果不甚理想。基于Fatti近似的弹性波阻抗方法，充分利用了叠前资料进行反演，包含了丰富的岩性及流体信息，但其小角度时的算法不稳定及建立在“湿”岩石背景假设条件下的反演精度不高的缺点也很明显。改进后的Fatti近似公式算法更加稳定且建立了基于真实岩石物理参数的变量关系，提高了反演精度。应用实例表明应用从弹性阻抗反演数据体中获得的λ-μ-ρ参数进行交会，对苏里格气田低含气饱和度的气层检测效果明显，很好地反映了储层信息。

2011

0.0

张广智, 郑静静, 印兴耀, 等. 基于Curvelet变换的角度流体因子提取技术[J]. 物探与化探, 2011, 35(4): 505-510.

According to the differences between angle gather data and multiscale and multi-direction characteristics of Curvelet transform, this paper proposes the utilization of angle fluid factor to discriminate different fluids. Models and real seismic data are used to test the method. The result is reliable, and the location and range of the reservoir can be satisfactorily obtained. In combination with other attributes, the method can provide better information for fine description of the reservoir. Making reference to cross-equalization methods of time-lapse seismic data, the wavelet cross-equalization method is used to equalize angle gather data. Then, Curvelet domain fluid anomaly separation technique is used to separate background field information (rock frame information) from fluid information, and the anomaly of the interesting layer can be obtained.

1. School of Geosciences,China University of Petroleum,Qingdao 266555, China; 2. International Department of Shengli Geophysical Company,SINOPEC,Dongying 257084, China

从角度道集数据出发,充分利用它们之间的差别,流体信息和骨架信息在尺度和方向上的差别,以及Curvelet变换的多尺度性和多方向性,提出应用角度流体因子属性进行流体识别的方法。参考时移地震数据的互均衡方法提出子波均衡法,对各个角道集数据进行均衡。然后,利用背景场信息(骨架信息)和流体信息在curvelet域分布的不同,将其进行逐步分离,得到目的层处的异常。把角度流体因子应用到模型与实际地震数据中,计算结果证明了其应用价值,可以准确地判定储层的位置及范围。进一步的与其他属性结合,为油藏精细描述提供较为可靠的依据。

2010

0.0

... nsberg等人^[15]建议用贝叶斯方法进行反演,以获取后验概率密度的样本,这里假定基于地质统计学的先验信息和似然函数都服从高斯分布,那么乘积得到的后验信息就是非高斯分布,即不能得到后验概率密度的解析解 ...

2000

0.0

... 基于蒙特卡洛抽样的反演方法结合了Metropolis算法、FFT-MA模拟算法^[16]和GDM更新算法^[17],可以为先验信息提供多参数扰动 ...

2000

0.0

... 基于蒙特卡洛抽样的反演方法结合了Metropolis算法、FFT-MA模拟算法^[16]和GDM更新算法^[17],可以为先验信息提供多参数扰动 ...

2011

0.0

... 另外,可以根据弹性阻抗反演方法直接反演得到拉梅参数、剪切模量和流体因子等其他反映岩性和流体的参数,如表1所示^[18],选取不同的AVO近似式,就可以得到不同的反演参数 ...

2001

0.0

... 2 随机反演理论在贝叶斯框架下进行反演问题的求解,假设噪声(似然函数)和先验分布均服从高斯分布,根据贝叶斯理论^[19] ...

1995

0.0

... FFT-MA方法通过快速傅里叶变换(FFT)简化了Oliver^[20]提出的滑动平均(MA)模拟方法的计算,表达式可以简要表示为 ...

1978

0.0

... FFT-MA模拟能够重构出满足指定变差结构和指定网格大小的数据,但由于它是一种非条件模拟方法,不满足硬数据(已知井资料),在实际应用时采用Journel和Huijbregts^[21]提出的克里金条件化方法进行条件化处理,从而该方法完全可以和经典的序贯模拟方法相媲美,并可有效地克服经典的序贯模拟方法计算耗时、耗内存等问题,提高反演方法的计算效率 ...

1998

0.0

... GDM最早由Hu等^[22]提出,用来逐步修改高斯分布的储层模型,其后被扩展到非高斯分布的序贯指示模拟^[23] ...

1999

0.0

... GDM最早由Hu等^[22]提出,用来逐步修改高斯分布的储层模型,其后被扩展到非高斯分布的序贯指示模拟^[23] ...

1995

0.0

... Metropolis抽样是一种基于蒙特卡洛的抽样方法^[24] ...

1996

0.0

... Gelman等人发现,高维分布的接受概率约为23%^[25],所以应该调整各参数,例如GDM扰动区域、GDM算法中p的取值、变差函数的选取、Metropolis接受准则的常数k和温度T等,使接受概率保持在23%左右 ...