基于矢量波场分离的TI介质逆时偏移

引用本文

任丽娟, 李振春, 王延光, 刘兴达, 孙小东. 基于矢量波场分离的TI介质逆时偏移[J]. 物探与化探, 2015,39(1): 196-202.
REN Li-Juan, LI Zhen-Chun, WANG Yan-Guang, LIU Xing-Da, SUN Xiao-Dong. Reverse-time migration for TI medium based on vector wavefield separation[J]. Geophysical and Geochemical Exploration, 2015,39(1): 196-202. 复制到剪切板

Doi:10.11720/wtyht.2015.1.32
Permissions

《物探与化探》编辑部所有

基于矢量波场分离的TI介质逆时偏移

任丽娟¹, 李振春¹, 王延光², 刘兴达¹, 孙小东¹

1.中国石油大学(华东) 地震波传播与成像实验室,山东青岛 266580

2.中国石化胜利油田分公司物探研究院,山东东营 257068

作者简介: 任丽娟(1987-),女,河北人,现为中国石油大学(华东)硕士研究生,主要从事地震波传播与成像方面的工作。

收稿日期: 2014-06-13

基金: 国家高技术研究发展计划(863计划)(2011AA060301); 国家科技重大专项项目(2011ZX05006-002)

摘要

基于两步法分离各向异性矢量波波场,第一步,将各向异性波动方程进行相似变换(使其具有明确直观的运动学和动力学特征),使其投影在各向同性方向上;第二步,各向异性介质传播算子波场分离基础上的波形校正,将投影于各向同性方向上的波场校正回各向异性方向上,最终达到各向异性波场分离的结果。笔者首先对VTI介质进行试算,以证明其可行性;此外,将地表数据进行分解,即所采集到的多分量地震数据在进行偏移成像之前先进行数据分解,得到纯净的qP波数据、qSV波数据以及qSH波数据,通过地表数据的分解将成像过程变成一个可控过程,通过对地表数据输入的控制得到我们所希望的成像结果分量,可以减少无谓的计算;对Hess模型正演炮记录进行了数据分解,并对其进行了逆时偏移成像以验证理论的可行性。

关键词: 各向异性; 矢量波场; 逆时偏移; 数据分解

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2015)01-0196-07

Reverse-time migration for TI medium based on vector wavefield separation

REN Li-Juan¹, LI Zhen-Chun¹, WANG Yan-Guang², LIU Xing-Da¹, SUN Xiao-Dong¹

1.SWPI,China University of petroleum(Huadong),Qingdao 266580,China

2.GRI of Sinopec Shengli Oilfield Branch,Dongying 257068,China

Abstract

Two-step separation was conducted for anisotropy vector wavefield.The first step is to make the anisotropic elastic wave equation in the polarization direction of the projection isotropic so that it has clear and intuitive kinematic and dynamic characteristics;the second step is to calculate anisotropic medium propagator wavefield separation waveform correction based on the correction of the projected direction of the wavefield in the isotropic direction back to the anisotropic direction, and ultimately the anisotropic wavefield separation can be achieved.First of all,the test of VTI media proves its feasibility.In addition,the authors put forward the surface data decomposition,namely,data decomposition is conducted for collected multicomponent seismic data before the migration imaging.In order to get the pure qP wave,qSH wave and qSV wave data the authors conducted the surface data input control to obtain the satisfactory imaging results of components and make imaging decomposition of the surface data performed in a controlled process,thus reducing unnecessary computation.The authors conducted decomposition of Hess forward modeling shot record data and reverse-time migration imaging.

Keyword: anisotropy; vector wavefield; reverse time migration; data decomposition

Show Figures

随着地震勘探日趋向着深层复杂地区发展, 面向复杂地区成像的地震处理成像方法研究越来越受到重视, 由于地球广泛存在波动各向异性^[1], 如何对各向异性地区(其中以横向各向异性介质最为常见, 简称TI介质)进行精细成像, 逐渐成为了地球物理界研究的重点。逆时偏移作为全波场成像有着诸如对高陡构造成像较好、适应横向速度剧烈变化且能对回转波及棱柱波进行成像等优势, 将其应用到各向异性介质的精细偏移成像有着先天的优势^{[2, 3, 4, 5, 6]}。

使用多分量数据进行矢量波偏移主要有两种方法, 第一种是将弹性波记录数据进行分解, 得到纵横波数据, 然后使用分解后的数据进行声波偏移成像, 也称为拟声波成像^{[7, 8]}。该方法目前应用较为广泛, 但是这个理论是基于纵横波在地表可以完全分离的基础上的, 而在各向异性介质中往往很难做到^{[9, 10]}。第二种方法则是对全波场进行矢量波延拓, 在每个采样时间点进行波场分离, 再使用分离后的波场进行成像, 其偏移方法主要有逆时偏移^[11]和克希霍夫偏移^[12]。

传统各向异性成像方法主要是对波动方程进行近似, 推导出拟声波方程进行纵波成像^{[13, 14, 15, 16, 17, 18, 19, 20]}。虽然目前对于此方向的研究相对较多, 但都难以完全消除横波对纵波的影响, 同时由于其对波动方程进行了近似, 在损失一部分能量的同时也可能会人为加入某些噪声^[21], 导致最终成像结果的误差。此外地下介质被认为是完全弹性介质^[22], 所以使用矢量波进行各向异性介质的成像既满足对于地下构造精细成像的无近似要求, 又有明确的物理意义(满足运动学和动力学特征)。但针对基于双程波动方程的各向异性介质矢量波偏移方法的研究相对较少, 原因是巨大的计算量以及无法完全分离耦合较为强烈的各向异性弹性波场。

各向同性介质矢量波场分离的主要方法是使用亥姆霍兹分解^[23], 但是由于在各向异性介质中波传播的方向发生了偏离, 其振动方向并不再是纵波与其相同、横波与其垂直的关系, 所以使用亥姆霍兹分解并不能很好地将各向异性介质中的耦合纵横波分离^[24]。Yan和 Sava^[25]在2009年提出了使用qP波的方法改进亥姆霍兹分解, 使其适应各向异性介质, 并在横向各向同性介质上做了模型试算, 根据波传播和振动的关系阐述了其分离波场的明确意义。但是, 使用qP波的方法分离纵横波需要大量使用傅里叶变换, 这十分耗时且运算量巨大, Zhang 和 McMechan^[26]以及Yan 和Sava^[27]在此基础上使用了一些相关近似, 使其减小了运算量。

基于两步法分离各向异性矢量波波场:第一步, 将各向异性波动方程进行相似变换(使其具有明确直观的运动学和动力学特征), 并投影在各向同性方向上; 第二步, 各向异性介质传播算子波场分离基础上的波形校正, 将投影于各向同性方向上的波场校正回各向异性方向上, 最终达到各向异性波场分离的结果。此外, 将地表数据进行分解, 即所采集到的多分量地震数据在进行偏移成像之前先进行数据分解, 使用分离后的纵横波场进行逆时偏移成像。

1 基本原理

1.1 各向异性矢量波场构建

各向异性非均质介质波动方程可以表示为

$\begin{matrix} ρ \frac{\partial^{2} U}{\partial t^{2}} = L (C L^{T} U) + ρF, \end{matrix}$ （1）

式中:

$\begin{matrix} \begin{matrix} C = [\begin{matrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} \\ c_{21} & c_{22} & c_{23} & c_{24} & c_{25} & c_{26} \\ c_{31} & c_{32} & c_{33} & c_{34} & c_{35} & c_{36} \\ c_{41} & c_{42} & c_{43} & c_{44} & c_{45} & c_{46} \\ c_{51} & c_{52} & c_{53} & c_{54} & c_{55} & c_{56} \\ c_{61} & c_{62} & c_{63} & c_{64} & c_{65} & c_{66} \end{matrix}]; \\ L = [\begin{matrix} \frac{\partial}{\partial x} & 0 & 0 & 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y} \\ 0 & \frac{\partial}{\partial y} & 0 & \frac{\partial}{\partial z} & 0 & \frac{\partial}{\partial x} \\ 0 & 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0 \end{matrix}]; \end{matrix} \end{matrix}$

U=(u_x, u_y, u_z)^T, 为位移矢量; ρ 为密度, C为刚度矩阵, F为体源, L为偏微分算子矩阵。

式(1)描述了各向异性完全弹性介质不同时刻的传播规律以及位移情况, 如果加以初始以及边界条件, 就可以构成特定的地震波动力学问题。介质的各向异性是由刚度矩阵来决定的, 它确定了应力应变关系, 但是, 弹性常数并没有明确的物理意义, 其表示十分不直观, 也导致了在研究地震波传播的时候, 决定其传播的相速度隐藏在波动方程的系数中(弹性常数)。为了方便研究和实际应用, 提出了用来表征TI介质性质的一套参数, 称为Thomsen参数^[28], 其表示形式为

$\begin{matrix} \begin{matrix} v_{p 0} = \sqrt[]{\frac{C_{33}}{ρ}}, v_{s 0} = \sqrt[]{\frac{C_{55}}{ρ}}, ε = \frac{C_{11} - C_{33}}{2 C_{33}}, \\ γ = \frac{C_{66} - C_{44}}{2 C_{44}}, δ = \frac{(C_{13} + C_{44})^{2} - (C_{33} - C_{44})^{2}}{2 C_{33} (C_{33} - C_{44})} 。 \end{matrix} \end{matrix}$ （2）

式中:v_p0表示qP波垂直于对称面的相速度; v_s0表示qS波垂直于对称面的相速度; ε 、γ 及δ 三个无量纲因子可以表示横向各向同性弹性介质的各向异性强弱。

1.2 各向异性矢量波波场分离

在横向各向同性(TI)介质中, 可以通过使用qP波和qS波的偏振方向来分离qP波和qS波, 使其表示偏振方向的算子可以真正地表示出各向异性介质中qP波和qS波的偏振方向。使用qP波作为例子, qP波分量可以通过使用虚微分算子分离^[25]

$\begin{matrix} q \dot{P} = \nabla_{a} \cdot W = L_{x} [W_{x}] + L_{y} [W_{y}] + L_{z} [W_{z}], \end{matrix}$ (3)

式中:L_x, L_y, L_z表示对iu_x, iu_y, iu_z作傅里叶逆变换的结果; L[]表示各向异性波场分离中的空间滤波算子; L_x, L_y, L_z分别代表各向异性介质中x, y和z方向的虚导数算子, 它们是由介质的内部参数所决定的, 所以不同位置的虚导数算子一般也不同。

通过求解Christoffel方程^[10]

$\begin{matrix} [G - ρ V^{2} I] U = 0 \end{matrix}$ (4)

能够得到U。其中:G表示Christoffel矩阵, G_ij=C_ijkln_jn_l, C_ijkl表示刚度常数, n_jn_l表示在j和l方向的单位矢量波, i, j, k, l=1, 2, 3。V相当于矩阵G的本征值, 也表示不同波(纵横波)的相速度。以VTI介质为例, 由于是VTI介质, 所以根据其对称性可以设k_y为0, 则式(4)可写成

$\begin{matrix} [\begin{matrix} c_{11} k_{x}^{2} + c_{55} k_{z}^{2} - ρ V^{2} & 0 & (c_{13} + c_{55}) k_{x} k_{z} \\ 0 & c_{66} k_{x}^{2} + c_{55} k_{z}^{2} - ρ V^{2} & 0 \\ (c_{13} + c_{55}) k_{x} k_{z} & 0 & c_{55} k_{x}^{2} + c_{33} k_{z}^{2} - ρ V^{2} \end{matrix}] [\begin{matrix} u_{x} \\ u_{y} \\ u_{z} \end{matrix}] = 0 \end{matrix}$ (5)

的形式。式中Christoffel矩阵中第二行表示的是qSH波的偏振方向, 而qP波和qSV波在垂直平面是与qSH波不耦合的, 第一行和第三行分别表示qP波和qSV波的偏振方向。

构建各向异性介质传播算子可以有效地对偏振方向较各向同性有明显变化的各向异性介质进行波场分离。但是, 由于要反复使用傅里叶变换导致其运算量巨大, 且单纯使用此算子物理意义并不明确。为了降低计算量且同时体现其运动学和动力学特征, 使用分步qP波方法进行上述过程。

第一步:将Christoffel方程即式(4)作相似变换, 分别对刚度矩阵和波场作对M_P方向的投影, 再将方程转换到时间空间域得到qP波方程, 其中:M_p= $\begin{matrix} [\begin{matrix} k_{x} & 0 \\ 0 & k_{z} \end{matrix}] \end{matrix}$ , 使C→ M_pC $\begin{matrix} M_{p}^{- 1} \end{matrix}$ , $\begin{matrix} \dot{u} \end{matrix}$ → M_p $\begin{matrix} \dot{u} \end{matrix}$ , 可得方程^[15]

$\begin{matrix} \{\begin{matrix} \frac{\partial^{2} u_{px}}{\partial t^{2}} = c_{11} \frac{\partial^{2} u_{px}}{\partial x^{2}} + c_{44} \frac{\partial^{2} u_{px}}{\partial z^{2}} + (c_{13} + c_{44}) \frac{\partial^{2} u_{pz}}{\partial x^{2}}, \\ \frac{\partial^{2} u_{pz}}{\partial t^{2}} = (c_{13} + c_{44}) \frac{\partial^{2} u_{px}}{\partial z^{2}} + c_{44} \frac{\partial^{2} u_{pz}}{\partial x^{2}} + c_{33} \frac{\partial^{2} u_{pz}}{\partial z^{2}} 。 \end{matrix} (6) \end{matrix}$

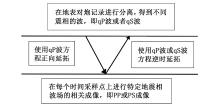
第二步:通过分析其投影的量对所得波场进行基于传播算子的校正。现在已知各向同性传播算子v_p=(k_x, k_z), 各向异性传播算子w_p=(a_x, a_z)和已得到的投影后求得的波场 $\begin{matrix} {\dot{u}}_{p} \end{matrix}$ =( $\begin{matrix} {\dot{u}}_{x} \end{matrix}$ k_x, $\begin{matrix} {\dot{u}}_{z} \end{matrix}$ k_z), 目标是求取校正后的波场 $\begin{matrix} {\dot{u}}_{p} \end{matrix}$ '=( $\begin{matrix} {\dot{u}}_{x} \end{matrix}$ a_x, $\begin{matrix} {\dot{u}}_{z} \end{matrix}$ a_z), 所以只需求取校正算子L_x=F^-¹(a_x/k_x), L_z=F^-¹(a_z/k_z)。

1.3 各向异性矢量波逆时偏移

通常可以通过地震采集系统得到某一地区的炮记录, 通过对其进行不同震相的分离得到qP波和qS波炮记录, 即为地表数据分解, 将分离好的数据使

用传统弹性波方程波场逆时反推, 再根据qP波方程正向延拓所得到的波场在同一时刻进行相关成像, 即为最终的成像值(图1)。由上可知, 通过地表数据的分解可以大量减少运算复杂程度和流程的复杂程度, 使成像过程更为清晰明了。

	Figure Option View Download New Window
	图1 基于地表数据分解的各向异性逆时偏移示意

关于进行地表数据分解, 方法等同于之前的qP波波场分离, 以二维情况为例, 对于qP波, 求取u_p_x= $\begin{matrix} \frac{\partial u_{x}}{\partial x} \end{matrix}$ 和u_p_z= $\begin{matrix} \frac{\partial u_{z}}{\partial z} \end{matrix}$ ; 对于qSV波, 求取u_sv_x= $\begin{matrix} \frac{\partial^{2} u_{x}}{\partial x \partial z} \end{matrix}$ 和u_sv_z= $\begin{matrix} \frac{\partial^{2} u_{z}}{\partial x^{2}} \end{matrix}$ 。上述过程较易推广到三维, 可分解出qP波, qSV波和qSH波, 之后可进行特定相位的成像。

2 模型试算

使用均匀各向异性VTI介质验证波场分离效果, 参数如表1所示。求取其校正算子, 并作用在第一步所求得的px分量和pz分量上, 再将结果相加得到最终结果, 如图2所示。

表1 均匀VTI介质参数

	Figure Option View Download New Window
	图2 均匀各向异性VTI介质波场分离效果 a— px分量; b— pz分量; c— L_x校正算子; d— L_z校正算子; e— 亥姆霍兹分解所得的qP波; f— 校正算子所得到的qP波

由图2e、图2f可见, 通过校正算子所得到的纵波相对通过亥姆霍兹分解所得到的纵波较为纯净, 亥姆霍兹分解所得纵波内部横波残留肉眼可见, 而通过校正算子所得到的纵波内部几乎无残留波形, 表明此方法分解的纵波单一无横波掺杂。

然后使用qP波方程与脉冲源的传统波动方程进行走时对比, 对比其运动学特征是否一致。通过图3可知, 其走时完全一致, 说明qP波方程和传统波动方程(地震波在地下传播的真实情况)的运动学特征是一致的, 某相同时刻两个方程所得到的波场快照如图3所示。

	Figure Option View Download New Window
	图3 qP波方程(左)与脉冲源传统波动方程(右)走时对比

接着, 我们要对其动力学特征进行分析, 使用传统波动方程和qP波波动方程进行单点振幅及其相位对比, 如图4所示, 其振动相位完全一致, 振幅虽有所差异但大体相差不多, 表明其动力学特征也是一致的。通过对qP波波动方程的运动学和动力学特征进行分析, 说明其可以表征明确的物理意义, 并且其运动学和动力学特性都与实际地下的地震波传播情况相同。

	Figure Option View Download New Window
	图4 传统波动方程与qP波波动方程单点振幅及相位对比

为验证上述地表数据分离的正确性, 使用Hess模型的单炮数据进行模拟分离试算。单炮接收范围为600个网格, 炮点位于中间位置, 采样间隔为0.5 ms, 采样时间为2.5 s, 分离结果如图5。可见, 通过地表数据分离, qP、qS波能很好地分离出来。

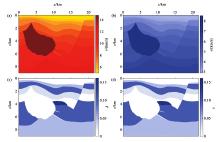
下面对Hess模型进行偏移成像。 Hess模型的纵波速度场、横波速度场各向异性参数δ 和各向异性参数ε 如图6所示, 模型大小为横向为21 702 m, 深度为9 000 m, 被剖分为3 617× 1 500个网格, 网格横向采样间隔为6 m, 纵向采样间隔为6 m。震源使用爆炸震源激发, 主频为30 Hz, 每炮的范围为横向2 000道接收, 检波点间隔为每5道接收一次, 第一炮位于1 000个网格点即6 000 m处, 以此向右移动, 炮间距为10个网格即60 m, 共158炮, 即炮点范围是从1 000个网格点到2 580个网格点, 检波点接收范围为(0~2 000)到(1 580~3 580), 正演模拟时间记录长度为3 s, 时间采样间隔为0.2 ms。

	Figure Option View Download New Window
	图5 Hess模型单炮数据分离试算 a— 炮记录z分量; b— 炮记录x分量; c— 分离后qP波分量; d— 分离后qS波分量

	Figure Option View Download New Window
	图6 Hess模型速度场及各向异性参数 a— 纵波速度场; b— 横波速度场; c— 各向异性参数δ 场; d— 各向异性参数ε 场

对地表炮记录数据进行数据分解后, 使用分离的纵横波场进行成像, 图7为Hess模型逆时偏移pp分量和ps分量。可以看出, 表层层位清晰可见, 地下盐丘轮廓明显, 且同相轴清晰、能量较强, 地下几个各向异性块成像干净明显, 地下裂缝处成像位置准确, 右边高陡构造成像较好, 体现了逆时偏移对于高陡构造成像的优势。由于模型地下构造的复杂性, 地震波在地下会多次反射产生回转波、棱柱波等多种特殊波形, 而在图7中并没有看到由这些波形产生的成像假象, 所以, 可以说明逆时偏移同样可以通过对这些特殊波形进行成像, 来加强地下构造处同相轴的能量。

	Figure Option View Download New Window
	图7 Hess模型偏移结果 a— pp分量; b— ps分量

3 结论

基于两步波场分离技术, 对地表数据进行分解, 即所采集到的多分量地震数据在进行偏移成像之前先进行数据分解, 得到纯净的qP波数据、qSV波数据以及qSH波数据, 通过地表数据的分解可以将成像过程变成一个可控过程, 通过对地表数据输入的控制得到我们所希望的成像结果分量, 可以减少无谓的计算。基于弹性波传播算子的波场分离方法能够分离出特定震相的地震波, 有着较为明确的物理意义, 且相对于传统的亥姆霍兹分解有着更高的精度。传播算子只与刚度矩阵有关, 因此推广到一般各向异性较为方便。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	吴国忱. 各向异性地震波传播与成像[M]. 东营: 中国石油大学出版社, 2006. [本文引用:1]
[2]	Baysal E D, Kosloff D, Sherwood J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. [本文引用:1]
[3]	Chang W, McMechan G A. 3D acoustic prestack reverse-time migration[J]. Geophysical Prospecting, 1990, 38(7): 737-755. [本文引用:1]
[4]	张春燕, 李振春, 孙小东. 逆时偏移方法技术进展综述[J]. 勘探地球物理进展, 2010, 33(5): 309-317. [本文引用:1]
[5]	屈念念, 李家斌. 基于P + S 波震源的弹性波叠前逆时偏移方法[J]. 物探与化探, 2013, 37(5): 859-865. [本文引用:1]
[6]	Liu W, Wang Y. Target-oriented reverse time migration for two way prestack depth imaging[J]. SEGTechnical Program Expand ed Abstracts, 2008, 27(1): 2326-2330. [本文引用:1]
[7]	Sun R G. A McMechan. Scalar reverse-time depth migration of prestack elastic seismicdata[J]. Geophysics, 2001, 66(5): 1519-1527. [本文引用:1]
[8]	何兵寿, 张会星. 多分量波场的矢量法叠前深度偏移技术[J]. 石油地球物理勘探, 2006, 41(4): 369-374. [本文引用:1]
[9]	Etgen J T. Prestacked migration of P and SV-waves[C]//58^th Ann. Internat Mtg. , Soc. Expi. Geophys. Expand ed Abstracts, 1988: 972-975. [本文引用:1]
[10]	Alkhalifah T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631. [本文引用:2]
[11]	Chang W F, McMechan G A. Reverse-time migration of offset vertical seismic profiling data using the excitation time imaging condition[J]. Geophysics, 1986, 51(1): 67-84. [本文引用:1]
[12]	Hokstad K. Multicomponent kirchhoff migration[J]. Geophysics, 2000, 65(2): 861-873. [本文引用:1]
[13]	Du X, Fletcher R P, Fowler P J. Pure P-wave propagators versus pseudo acoustic propagators for RTM in VTI media[C]//72^nd EAGE Conference & Exhibition, 2010. [本文引用:1]
[14]	Duveneck E, Bakker P. Stable P-wave modeling for reverse-time migration in tilted TI media[J]. Geophysics, 2011, 76(2): 65-75. [本文引用:1]
[15]	Cheng J B, Kang W. Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators[J]. Geophysics, 2013, 79(1): 1-18. [本文引用:2]
[16]	Tessmer E. Reverse-time migration in TTI media[C]//Denver: 2010 SEG Annual Meeting, 2010, 42(3): 3193-3197. [本文引用:1]
[17]	康玮, 程玖兵. 横向各向同性介质拟声波方程及其在逆时偏移中的应用[J]. 地球物理学报. 2012, 55(3): 1033-1045. [本文引用:1]
[18]	Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic media[J]. Geophysics, 2009, 74(6): 179-187. [本文引用:1]
[19]	Zhan G, Pestana R C, Stoffa P L. Decoupled equations for reverse time migration in tilted transversely isotropic media[J]. Geophysics, 2012, 77(2): 37-45. [本文引用:1]
[20]	王娟, 李振春, 孙小东, 等. TTI介质逆时偏移成像[J]. 石油地球物理勘探, 2012, 47(4): 573-577. [本文引用:1]
[21]	Zhang H, Zhang Y. Reverse time migration in 3D heterogeous TTI media[J]. SEG Technical Program Exapand ed Abstracts, 2008, 27: 2196-2200. [本文引用:1]
[22]	Gray S H, Etgen J, Dellinger J, et al. Seismic migration problems and solutions[J]. Geophysics, 2001, 66(5): 1622-1640. [本文引用:1]
[23]	Yan J, Sava P. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 2008, 73(6): 229-239. [本文引用:1]
[24]	Yan J, Sava P. 3D elastic wave mode separation for TTI media[C]//79^th Annual International Meeting, SEG, Expand ed Abstracts, 2009, 28: 4294-4298. [本文引用:1]
[25]	Yan J, Sava P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74 (5): WB19-WB32. [本文引用:2]
[26]	Zhang Q, McMechan G. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. [本文引用:1]
[27]	Yan J, Sava P. Improving the efficiency of elastic wave-mode separation for heterogeneous tilted transverse isotropic media[J]. Geophysics, 2011, 76(4): T65-T78. [本文引用:1]
[28]	牛滨华, 孙春岩. 裂隙各向异性介质 2. 5D弹性波场数值模拟[J]. 中国地质大学学报, 1995, 20(1): 107-111. [本文引用:1]

2006

0.0

... 随着地震勘探日趋向着深层复杂地区发展,面向复杂地区成像的地震处理成像方法研究越来越受到重视,由于地球广泛存在波动各向异性^[1],如何对各向异性地区(其中以横向各向异性介质最为常见,简称TI介质)进行精细成像,逐渐成为了地球物理界研究的重点 ...

1983

0.0

... 逆时偏移作为全波场成像有着诸如对高陡构造成像较好、适应横向速度剧烈变化且能对回转波及棱柱波进行成像等优势,将其应用到各向异性介质的精细偏移成像有着先天的优势^[2,3,4,5,6] ...

1990

0.0

2010

0.0

张春燕, 李振春, 孙小东. 逆时偏移方法技术进展综述[J]. 勘探地球物理进展, 2010, 33(5): 309-317.

逆时偏移(RTM)利用双程波动方程,基于时间逆时外推对波场进行重构,理论上无倾角限制,可以实现对回转波、棱镜波以及多次波的正确成像,获得精确的动力学信息,具有良好的保幅性.然而,庞大的存储空间需求和计算量以及固有的低频成像噪声,使得RTM无法得到广泛的应用.针对上述问题,分析、对比了各种逆时偏移方法技术及其应用效果,测试了偏移去噪的几种方法,最后对逆时偏移的发展方向作了展望.

2013

0.0

屈念念, 李家斌. 基于P + S 波震源的弹性波叠前逆时偏移方法[J]. 物探与化探, 2013, 37(5): 859-865.

Based on elastic wave equation,the authors deduced first-order velocity-stress elastic wave-equation with decoupling of compressional wave and shear wave and no converted wave under the condition of two-dimensional inhomogeneous media,which could not only make the implementation of vector migration and ensure the quality of migration,but also avoid the production of other kinds of converted interference wave.Starting from theories of exciting time image condition and reflection coefficient,in combination with first-order velocity-stress elastic wave-equation characterized by decoupling of compressional wave and shear wave and no converted wave,the authors put forward the image condition and migration method suitable for simulated data based on a combined P + S source.This paper has provided the theoretic record migration results of two typical models,and tests show that the method proposed in this paper can make the wavefiled produced by a combined P + S source return to the position accurately,and improve the processing precision of information.

基于弹性波动方程,推导了二维非均匀介质条件下纵横波解耦且无转换波的一阶速度—应力弹性波方程,使得弹性波在延拓过程中实现矢量偏移保证偏移质量,且不产生其他类型的转换干扰波。从激发时间成像条件以及反射系数理论出发,并与纵横波解耦且无转换波的一阶速度—应力弹性波方程结合,给出了适用于P+S波震源模拟数据的成像条件以及偏移方法。文中给出了两个典型模型的理论记录的偏移结果,试验表明,笔者提出的方法能够对P+S波震源的产生的波场准确归位,提高资料处理精度。

2008

0.0

2001

0.0

... 使用多分量数据进行矢量波偏移主要有两种方法,第一种是将弹性波记录数据进行分解,得到纵横波数据,然后使用分解后的数据进行声波偏移成像,也称为拟声波成像^[7,8] ...

2006

0.0

何兵寿, 张会星. 多分量波场的矢量法叠前深度偏移技术[J]. 石油地球物理勘探, 2006, 41(4): 369-374.

The paper studied a vector prestack depth migration method—prestack inverse-time depth migration for two components records in 2D isotropic medium. Firstly, staring from the elastic wave equation, high-order finite-difference format of elastic wave inverse-time continuation in isotropic medium was deduced in staggering grid space; then, proceeding from the eikonal equation, the seismic travel time at each underground point was computed by inverse-time finite-difference format. In order to ensure the causality of seismic propagation and adaptability to complicated model, expanding wave front method was used to track wave front and search global minimum, taking above mentioned computational results as imaging condition of elastic wave inverse-time migration. The prestack inverse-time depth migration of 2D multi-component data can be realised. The tests of model and real single-shot records showed the prestack inverse-time depth migration considered the vector feature of seismic wave, which is an effective vector wavefield processing technique

本文研究了二维各向同性介质中两分量记录的矢量法叠前深度偏移方法———叠前逆时深度偏移方法。首先从弹性波波动方程出发,在交错网格空间中推导了各向同性介质中弹性波逆时延拓的高阶有限差分格式;然后从程函方程出发,采用逆时差分格式求解地下各点的地震波走时。为确保算法满足地震波传播的因果性条件及其对复杂模型的适应性,用扩展波阵面算法追踪波前并搜索全局极小,以上述方法的计算结果作为弹性波逆时偏移的成像条件,实现二维多分量资料的叠前逆时深度偏移。模型试算和实际单炮记录试验表明,叠前逆时深度偏移方法考虑了地震波的矢量特征,是一种有效的矢量波场处理技术。

1988

0.0

... 该方法目前应用较为广泛,但是这个理论是基于纵横波在地表可以完全分离的基础上的,而在各向异性介质中往往很难做到^[9,10] ...

1998

0.0

... 该方法目前应用较为广泛,但是这个理论是基于纵横波在地表可以完全分离的基础上的,而在各向异性介质中往往很难做到^[9,10] ...

... 通过求解Christoffel方程^[10] ...

1986

0.0

... 第二种方法则是对全波场进行矢量波延拓,在每个采样时间点进行波场分离,再使用分离后的波场进行成像,其偏移方法主要有逆时偏移^[11]和克希霍夫偏移^[12] ...

2000

0.0

2010

0.0