要对散乱离散点数据点进行三角网格剖分, 必须得到数据点的边界, 数据点的边界可以人工读取也可以用算法识别。对于采集到的大量数据来说, 其边界点的数量必然也很多, 人工识别耗时耗力。为了提高实际工作效率, 采用美国数学学会主席Graham教授发明的凸包(convex hull)扫描算法。已知离散点集P{p₁(x, y), p₂(x, y), …, p_n(x, y)} 的凸包Ω 是指一个最小凸多边形, 满足P中的点在多边形边上或在其内, 凸包算法的目的是要找到这个最小凸多边形, 即数据点的边界。常见的凸包算法有分治法、快包法、增量式算法、Graham扫描法、Jarvis步进法等, 这些算法的时间复杂度从O(nlnn)到O(n²)^{[8, 9, 10, 11]}。

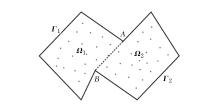
野外采集到的数据点集并不都是凸包, 可能会存在如图1中A、B处的凹边界, 仍然采用凸包算法则不能够识别凹边界。对应的办法是对数据点集进行分块, 得到多块子凸包Ω , 用凸包算法对每一个子凸包进行边界提取得到子边界Γ , 按逆时针拼接各个子边界, 得到数据点集的整个边界:Γ =Γ ₁∪ Γ ₂∪ …∪ Γ _n。

图1

	Figure Option ViewDownloadNew Window
	图1 散乱离散点数据点凹边界的分块搜索

常规网格化方法都是基于矩形网格进行插值的, 用数据坐标的最值得到一个能够包围所有数据点的矩形, 通过一定间距的网格剖分、插值, 得到每一节点的值。矩形网格化方法不仅不能模拟工区测网的实际形状, 成图之后还要根据数据边界对外推区域进行白化, 这无疑增加了额外计算量, 降低了工作效率。

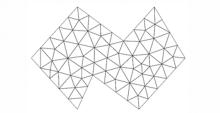
三角剖分对于数值分析(比如有限元计算)以及图形学来说, 是一项极为重要的预处理技术。基于Delaunay准则剖分的三角网格必须满足3个条件^{[12, 13]}:产生的三角形不相重叠, 不产生新的数据节点以及所有剖分出来的三角形的合集是点集P的凸包。三角网格剖分已经开发出了很多成熟的商业软件和算法, 如美国麻省理工学院Per-Olof Persson博士^[14]开发的Distmesh、加利福尼亚大学Jonathan Shewchuk教授^[15]开发的Triangle程序包, 都可以对各种形状进行剖分。在获得了数据点集的凸包边界后, 就可以用数据节点进网格剖分, 剖分后的三角网格顶点就是数据节点的位置(图2)。

图2

	Figure Option ViewDownloadNew Window
	图2 用边界和数据点进行三角剖分

剖分出三角网格后, 理论上就可以连接等值点作出等值线图, 但原始数据点太少, 得到的等值线由折线构成, 不光滑。因此, 需要在原来的网格内部剖分出尺寸更小的三角形, 新增加的三角形顶点的值可以采用线性插值的办法得到, 原来的三角形顶点的值仍然保留, 所以用这种方法插值不会超过原始数据的幅值范围。

图3

	Figure Option ViewDownloadNew Window
	图3 面积坐标插值原理示意

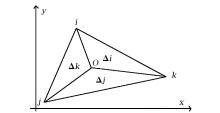
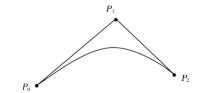
如图3所示, 设P_i(x, y)、P_j(x, y)、P_k(x, y)是某个三角单元的顶点, 将该三角单元内的插值点与3个顶点连线得到3个新的三角单元, 利用它们与原三角形面积的比值可以惟一确定该点的场值^{[16, 17]}:

u(x, y)=Liui+Ljuj+Lkuk,（1）

其中, 面积坐标L是x, y的线性函数。对所有加密剖分后的三角单元的顶点进行插值计算, 便可得到新顶点处的场值:

Lix, y=12∆yj-ykx+xk-xjy+xjyk-xkyj,

Ljx, y=12∆yk-yix+xi-xky+xkyi-xiyk,

Lkx, y=12∆yi-yjx+xj-xiy+xiyj-xjyi,

∆=12yj-ykxi-xk-yk-yixk-xj.（2）

经过第三步, 已经形成了更小的三角网格, 且节点上的场值已经通过线性插值的办法得到。确定等值线的条数, 就可以根据场值的最大、最小值得到每一条等值线的值。对于每一条等值线, 将所有三角形搜索一遍, 寻找该等值线的值对应的等值点, 连接所有等值点得到一条等值线。重复操作, 就可得到所有等值线^[18]。

由上面各式可进一步推出面积坐标

Li(x, y)+Lj(x, y)+Lk(x, y)=1,（3）

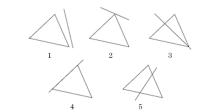
式中, L_i, L_j, L_k∈ (0, 1)。已知u_i, u_j, u_k为某个三角单元顶点处的场值, 结合上述各式可知, 该三角单元内任意一点的场值u∈ (min(u_i, u_j, u_k), max(u_i, u_j, u_k))。如果该等值点不在该三角单元的幅值之间, 则等值线不经过该三角形; 反之, 让搜索点的坐标在三角单元的边上循环, 当边上的点(x_i, y_i)满足u(x_i, y_i)=u₀(u₀为某条等值线的值), 则等值线经过该三角单元。等值线与三角单元有5种位置关系, 如图4所示。

图4

	Figure Option ViewDownloadNew Window
	图4 等值线与三角单元的5种位置关系

第四步得到的等值线仍然是由尺寸更小的折线构成, 不光滑, 需要对等值线进行光滑处理。光滑算法有很多, 比如分段多项式插值法、张力样条函数法、Bezier曲线法等^{[19, 20, 21]}。在此主要介绍Bezier曲线法, 它是用来光滑等值线的常用方法。

已知3个等值点P₀、P₁及P₂的坐标, 则二次贝塞尔曲线函数B(t)定义为^[22-23]:

B(t)=(1-t)2P0+2t(1-t)P1+t2P2,（4）

式中, t∈ [0, 1]。经过贝塞尔曲线光滑后, 便可得到如图5所示的光滑等值线 P0P2⌢。

图5

	Figure Option ViewDownloadNew Window
	图5 Bezier曲线光滑原理

应用高密度电阻率法得到的视电阻率数据, 由于在数据采集过程中地形高低起伏, 其反演电阻率剖面往往不是规则的倒梯形, 而是与勘探深度有关的不规则多边形。图6a为用凸包算法得到散乱数据点的边界和加密剖分后的插值网格, 然后连接各等值点得到未光滑前的等值线图如图6b, 用Bezier曲线得到光滑后的等值线(图6c), 在Surfer中采用克里格插值法对散乱数据网格化并白化后得到的等值线如图6d。

图6

	Figure Option ViewDownloadNew Window
	图6 本文方法与Surfer的反演电阻率成图结果对比

图6d中电阻率最大值为1 575 Ω · m, 最小值为669 Ω · m, 而原始数据最大值为1 613 Ω · m, 最小值为616 Ω · m。可见, 本方法与克里格插值方法一样, 都能清晰地反映异常体的形态, 但本方法不会改变原始数据的范围。

在实际金属矿产勘查工作中, 往往会用磁法对工区进行“ 扫面” , 得到数据量很大的散乱离散点数据。为了验证算法的稳定性, 采用云南某工区的磁异常数据进行成图, 共15条测线, 线距500 m, 测线沿北东向分布, 每条测线约60个测点, 点距50 m, 共906个散乱离散点。使用Surfer, 经克里格网格化插值得到的等值线如图7a, 用本文方法进行边界识别后剖分7 808个三角单元得到的等值线如图7b。

图7

	Figure Option ViewDownloadNew Window
	图7 磁异常数据的成图对比

图7显示, 本文方法明显比surfer得到的等值线光滑, 且两者皆有明显的正负异常, 可以确定磁异常的范围。图7a出现的锯齿状边界是因为Surfer在网格化过程中根据网格尺寸对边缘进行白化舍去, 而图7b的直线边界是根据散乱离散点数据最初的位置得到。表1显示, 相比其他网格化方法, 本文方法不需要白化, 成图速度快, 效率高。

表1

表1

表1 磁异常数据成图中各种网格化方法的效率比较 方法 最小值/nT 最大值/nT 时间/s 是否白化 理论 -823.90 843.70 克里格法 -633.59 726.99 1.03 是 径向基函数法 -794.07 820.35 1.80 是 自然邻点法 -476.90 644.58 0.09 否 本文方法 -823.90 843.70 0.16 否

表1 磁异常数据成图中各种网格化方法的效率比较